博弈视角下供应链企业守约的影响因素研究

刘 洋，刘 成

(湖北工业大学经济与管理学院，湖北 武汉 430068)

小微企业是我国国民经济的重要组成部分，在经济增长、增加就业、科技创新等方面发挥着不可替代的促进作用，但是融资难、融资贵的问题已经严重影响到其生存与发展[1]。姜付秀[2]、Berger[3]研究发现，造成这一困局的主要原因在于信息不对称。小微企业由于财务报表不健全、经营规模小、不确定因素高很难得到贷款[4]。而供应链金融在破解小微企业融资难题方面具有显著优势，其依托核心企业信用和真实贸易背景，围绕上下游企业融资需求，提供融资、结算、现金管理等金融服务，对融资结构与流程进行优化，降低了企业的融资成本，实现了供应链企业与金融机构的多方共赢[5-6]。我国应收账款余额的持续上升，资产证券化业务的快速增长，商务部、银保监会先后发布推动供应链金融服务实体经济的相关文件，都表明供应链金融市场未来具有广阔的发展空间[7]。

然而，在供应链金融快速发展的潮流中，供应链企业违约行为也频频出现。如2019年中粮信托未兑付项目“有机一号”事件，由于供应链金融中的部分经销商到期无法兑付贷款，其打造的农业供应链价值被破坏。又如“上海钢贸案”“青岛港骗贷”等事件，融资企业利用虚假仓单欺诈和套取资金，导致供应链金融的信用危机提升。显然，这些潜在风险不利于供应链金融的健康发展，如何降低企业存在的违约风险，激励企业守约还款，成为当前供应链金融领域亟待解决的问题。

基于以上分析，为探究影响供应链中企业守约的影响因素，本文以供应链金融中的应收账款质押融资模式为例，建立核心企业与中小企业守约的演化博弈模型，通过构造博弈双方守约的复制动态方程，对二者间的演化博弈均衡进行分析，以此刻画二者守约与违约的动态模型。本文的创新点主要体现在以下两个方面：第一，以供应链金融中的应收账款质押融资模式为例，运用演化博弈的方法从动态视角剖析供应链企业的守约问题，考虑到核心企业与小微企业的长期合作关系，避免了静态完全信息模型产生的“囚徒困境”问题；第二，基于有限理性理论，供应链金融参与主体的行为决策是不断进行适应性调整的，对不同情境下银行贷款利率、违约企业惩罚力度、合作产生额外收益等因素进行比较分析，探究核心企业与小微企业的稳定演化策略，从而为激励企业守约提供相应的对策建议。

1 供应链金融研究现状

供应链金融的发展为企业解决融资难的问题带来了巨大转机，特别是2007年《物权法》的实施，首次将应收账款和存货纳入我国动产担保范围，对中小企业出售应收账款弥补资金缺口具有重要现实意义(江伟，2016；王宗润，2015)[5,8]。付玮琼(2020)[9]指出，随着融资需求超过资金积累速度，形成了以核心企业为主导的供应链金融模式，中小企业借助业务关联方的核心企业信用做担保来贷款，分散了中小企业贷款风险，同时盘活了中小企业的生产经营，增加整个供应链链条的收益。

但是，我国的供应链金融仍处于发展的初级阶段，其内部的信用机制仍不健全，导致包括道德风险、市场风险和操作风险等在内的供应链金融风险问题。一方面，在核心企业主导的供应链金融模式中，其主导作用会产生依赖性垄断，推动风险的发生，导致中小企业融资中屡屡出现欺诈和套取现金等不良行为(付玮琼，2020；柴正猛，2020)[9-10]。另一方面，中小企业在获得贷款后，可能投资高风险项目，最终无法按时偿还贷款，对核心企业的信用造成损失。由此暴露出小微企业不能按时还款、核心企业信用损失的两难困境，所以，在供应链金融背景下研究小微企业与核心企业的违约问题具有现实意义，而探究供应链企业守约的影响因素成为破解这一难题的关键。

为了解决供应链金融出现的风险问题，国内外学者展开对影响企业违约机理的研究。Gu(2016)[11]指出，银行与企业之间的信息不对称加剧了企业的违约风险。由于银行放款前无法完全得知企业贷款后的偿还意愿、所投项目等信息，甚至于财务状况已经恶化，最终导致企业难以偿还债务(Carvalho，2019)[12]。此外，张路(2019)[13]通过构建应收账款质押融资模式中核心企业与中小企业的博弈模型，得出二者同时守约产生的额外收益越大，对违约企业的惩罚力度越大，越能推动中小企业选择守约的结论。

2 供应链企业守约模型

2.1 问题描述

供应链金融的发展为解决小微企业融资难的问题带来了巨大的推动作用，不仅盘活了中小企业的生产，同时提高了整个供应链的收益。但是不容忽视的现实问题是，供应链企业之间的违约现象，为供应链金融的可持续发展带来了巨大挑战。因此，为探究影响供应链企业守约的影响因素，本文基于应收账款质押融资模式展开研究，作为供应链金融的主要模式，其融资流程为：中小企业先与核心企业达成协议并签订合同，核心企业向中小企业发出应收账款票据作为支付承诺，中小企业将应收账款票据质押给银行，同时核心企业向银行作出支付承诺，银行向中小企业提供信用贷款，核心企业销货完毕后将应收账款支付给银行(图1)。

维持供应链金融长期有限运转的基本条件是核心企业按时支付货款、中小企业能够凭借银行提供的信用贷款进行正常的生产经营活动。如果其中一方或两方发生违约，则会导致供应链的中断，给银行和企业造成巨大损失。例如，中小企业发生违约，银行会向核心企业索要贷款，如果核心企业也选择违约不偿还贷款，则会降低企业的信用评级，导致银行的贷款利率上升，甚至不贷款给核心企业；同时，中小企业发生违约会导致核心企业不继续合作，造成供应链成员的巨大损失。基于以上分析，本文在张路(2019)[13]、李诗华(2015)[14]研究银行与企业动态博弈模型的基础上，以应收账款质押融资模式为例，依托有限理性假设，构建核心企业与中小企业的演化博弈模型，从长期动态演化视角分析供应链企业守约的策略选择问题，剖析其影响因素，弥补静态博弈下出现双方均不守约的“囚徒困境”问题。

图1 基于应收账款质押融资模式

2.2 模型假设

假设1：博弈双方为中小企业与核心企业，二者均有守约与违约两种选择。核心企业守约的概率为x，则违约的概率为1-x；中小企业守约的概率为y，则违约的概率为1-y。核心企业与中小企业的选择相互独立。

假设2：中小企业的应收账款总额为R，应收账款质押率为rm，则贷款金额为Rrm。中小企业可将应收账款质押融资取得的资金投入再生产，假设其再生产收益率为rs。核心企业可将应收账款资金在账期内投入再生产，假设其再生产收益率为rc。

假设3：供应链企业长期稳定合作会推动内部成本下降和外部信誉上升，假设由此带来的额外收益为A。中小企业如果违约核心企业会与其终止合作，银行将不再放贷，假设由此遭受的损失为PS。核心企业如果违约会影响其在银行的信用记录，银行会在之后的合作中对其降低贷款额度、提高贷款利率，假设由此遭受的损失为PC。

假设4：银行贷款利率为rL。

2.3 模型构建

中小企业与核心企业所有可能的选择如下。

1)当中小企业与核心企业均守约时，产品销售完毕后由核心企业将应收账款存入银行，银行扣除贷款本息后将余额支付给中小企业。此时核心企业的收益为Rrcm+A，中小企业的收益为Rrm(rS-rL)+A。

2)当中小企业违约而核心企业守约时，核心企业在销货后依旧将应收账款存入银行，中小企业违约不归还银行的贷款本息，代价为放弃银行扣除贷款本息后的余额。此时核心企业的收益为Rrc，中小企业的收益为Rrm(1+rS)-R(1-rm)-PS。

3)当中小企业守约而核心企业违约时，核心企业在销货后不再将应收账款存入银行，中小企业守约要归还银行的贷款本息，但损失了应收账款。此时核心企业的收益为R(1+rc)-PC，中小企业的收益为Rrm(rS-rL)-R。

4)当中小企业与核心企业均违约时，核心企业不支付银行应收账款，中小企业不偿还银行贷款本息，二者均会遭受违约损失。此时核心企业的收益为R(1+rc)-PC，中小企业的收益为Rrm(1+rS)-R(1-rm)-PS。

根据以上假设，构建核心企业与中小企业演化博弈的收益矩阵(表1)。

表1 核心企业与中小企业的演化博弈收益矩阵

3 演化博弈的均衡分析

3.1 演化稳定策略与复制动态方程

传统博弈论有两个苛刻假设，即完全理性和完全信息假设，演化博弈论不要求参与人是完全理性的，也不要求完全信息的条件。在方法论上，传统博弈论将重点放在比较静态均衡上，演化博弈论将博弈理论分析和动态演化过程结合在一起，强调的是一种动态均衡。

演化稳定策略指在博弈过程中，博弈双方由于有限理性和有限信息，不可能一开始就找到最优策略，只能不断模仿别人的有利策略并改进自己的不利策略。经过一段时间的模仿和改进，博弈双方都会趋于某个稳定策略。

复制动态方程指某一特定策略，在供应链参与者中被选择的概率关于时间的动态微分方程。复制动态方程是寻找演化稳定策略的工具，由于演化稳定策略对微小扰动具有稳健性，如果某博弈方由于偶然错误偏离了演化稳定策略，复制动态方程仍会使x或y回归到演化稳定策略x*或y*。

依据复制动态微分方程稳定性定理和演化稳定策略相关原理可知，当F(x)=0，F′(x)<0时，x为演化稳定策略点。

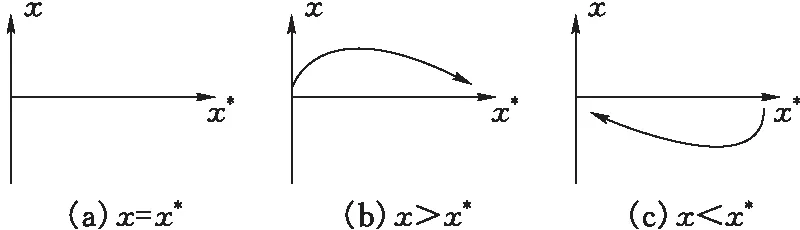
假设x的复制动态方程为F(x)=dx/dt，则使F(x)=0的点为稳定状态，但只有对微小扰动具有稳健性的稳定状态才是演化稳定策略，即当干扰使x低于x*时，F(x)=dx/dt>0；当干扰使x高于x*时，F(x)=dx/dt<0。换言之，当x=x*时，dF(x)/dx<0。

3.2 核心企业的复制动态方程

假设核心企业守约的期望收益为ECY，违约的期望收益为ECN，平均期望收益为EC，则：

ECY=y(Rrcm+A)+(1-y)Rrcm=yA+Rrcm

ECN=y[R(1+rc)-PC]+

(1-y)[R(1+rc)-PC]=R(1+rc)-PC

EC=xECY+(1-x)ECN

构造核心企业守约概率的复制动态方程：

F(x)=dx/dt=

x(ECY-EC)=x(1-x)(yA-R+PC)

令F(x)=0，得x=0,x=1或y*=(R-PC)/A

若y≠y*，则x=0,x=1为稳定状态；

若y=y*，则x∈[0,1]为稳定状态。

对F(x)求导可得：dF(x)/dx=(1-2x)(yA-R+PC)

1)若R-PC<0，即y*<0，则y>y*，此时x=1为演化稳定策略；

2)若R-PC>A，即y*>1，则y

3)若0

由此，可得核心企业的复制动态相位图(图2)。

图2 核心企业的复制动态相位图

3.3 中小企业的复制动态方程

假设中小企业守约的期望收益为ESY，违约的期望收益为ESN，平均期望收益为ES，则：

ESY=x[Rrm(rS-rL)+A]+

(1-x)[Rrm(rS-rL)-R]=

x(A+R)+[Rrm(rS-rL)-R]

ESN=x[(1+rS)-R(1-rm)-PS]+

(1-x)[Rrm(1+rS)-R(1-rm)-PS]=

Rrm(1+rS)-R(1-rm)-PS

ES=yESY+(1-y)ESN

构造中小企业守约概率的复制动态方程：

F(y)=dy/dt=y(ESY-ES)=

y(1-y)[x(A+R)-RrmrL-2Rr+PS]

令F(y)=0，得y=0,y=1或x*=(RrmrL+2Rr-PS)/(A+R)

若x≠x*，则y=0,y=1为稳定状态；

若x=x*，则y∈[0,1]为稳定状态。

对F(y)求导可得：dF(y)/dy=(1-2y)[x(A+R)-RrmrL-2Rr+PS]

1)若RrmrL+2Rrm-PS<0，即x*<0，则x>x*，此时y=1为演化稳定策略；

2)若RrmrL+2Rrm-PS>A+R，即x*>1，则x

3)若0

由此，可得中小企业的复制动态相位图(图3)。

图3 中小企业的复制动态相位图

3.4 演化均衡分析

对于一个由微分方程描述的群体动态，其均衡点的稳定性可由该系统的雅可比矩阵的局部稳定分析得出。本文使用雅可比矩阵的局部稳定分析方法来研究F(x)和F(y)组成的系统稳定性。

F(x)和F(y)组成系统的雅可比矩阵：

雅可比矩阵的行列式和迹分别为：

detJ=(1-2x)(yA-R+PC)(1-2y)[x(A+R)-

RrmrL-2Rrm+PS]-x(1-x)Ay(1-y)(A+R)

trJ=(1-2x)(yA-R+PC)+

(1-2y)[x(A+R)-RrmrL-2Rr+PS]

为了使博弈双方的收益更加符合实际情况增加约束条件：

1)当核心企业守约时，中小企业守约的收益大于违约的收益；

2)当核心企业违约时，中小企业守约的收益小于违约的收益；

3)当中小企业守约时，核心企业守约的收益大于违约的收益；

4)当中小企业违约时，核心企业守约的收益小于违约的收益，即

从而0

此时局部均衡分析的结果如表2所示。

表2 核心企业与中小企业的局部均衡分析

结合Friedma提出的判定方法，当雅可比矩阵J同时满足detJ>0,trJ<0时，均衡点才是演化稳定策略(Evolutionarily Stable Strategy，ESS)[15-16](高燕来，2020；Friedma，1998)。由表2可知，在核心企业与中小企业的博弈中，(0,0)和(1,1)是演化稳定策略点，分别对应(违约，违约)策略与(守约，守约)策略，(0,1)和(1,0)为不稳定点，(x*,y*)为鞍点，其他所有点都不是复制动态中收敛和具有抗扰动性质的稳定点。

将核心企业与中小企业的复制动态关系置于同一坐标平面中(图4)。

图4 核心企业与中小企业的复制动态及稳定性轨迹

由图4可知，由两个不稳定点A、C和鞍点D连成的折线可以看作是系统收敛于不同策略的分界线。初始状态在ABCD区域时，系统将收敛于策略(守约，守约)；初始状态在AOCD时，系统将收敛于策略(违约，违约)。两种策略都是演化稳定策略，都实现了博弈的纳什均衡，但只有策略(守约，守约)实现了博弈的帕累托最优。这是因为在核心企业与中小企业的多次重复博弈中，单方违约都将导致博弈无法持续进行，核心企业与中小企业要么选择合谋骗贷，要么选择共同守约。

3.5 守约博弈策略选择

要想提高核心企业与中小企业在多次重复博弈中选择(守约，守约)的演化稳定策略的概率，只有扩大区域ABCD的面积。假设核心企业与中小企业选择(守约，守约)的演化稳定策略的概率为P，则：

P=1-(x*+y*)/2=

1-[(RrmrL+2Rrm-PS)/(A+R)+(R-PC)/A]/2

下面讨论参数变化对选择(守约，守约)策略概率的影响。

1)dP/drL=-RrmrL/[2(A+R)]<0，故核心企业与中小企业选择(守约，守约)的演化稳定策略的概率与银行贷款利率负相关。银行贷款利率的上升更有可能引发中小企业信贷融资中的逆向选择问题，导致中小企业选择违约策略，核心企业为了减少损失，也会顺势选择违约策略。

2)dP/dPC=1/(2A)>0，dP/dPS=1/[2(A+R)]>0，故核心企业与中小企业选择(守约，守约)的演化稳定策略的概率与违约企业惩罚力度正相关。违约企业惩罚力度的上升增加了企业的违约成本，当违约成本大于违约收益时，企业便不会选择违约策略。

3)dP/dA=0.5[(RrmrL+2Rrm-PS)/(A+R)2+(R-PC)/A2]>0，故核心企业与中小企业选择(守约，守约)的演化稳定策略的概率与供应链企业长期稳定合作产生的额外收益正相关。对于核心企业而言，长期稳定合作会向外部传递企业经营稳定的信息，如果是上市公司可能会推动股价的上涨；对于中小企业而言，长期稳定合作会提升企业的信用，从而带来更多的合作机会和贷款机会。

4 对策与建议

针对供应链金融企业融资问题，本文以应收账款为研究对象，构建核心企业与中小企业的动态演化博弈模型，比较不同情境下影响供应链企业选择守约策略的影响因素，进一步探究提高核心企业与中小企业选择(守约，守约)策略概率的解决方案，得到以下结论。

1)核心企业与中小企业的博弈过程中存在两个演化渐进稳定策略，即双方同时选择守约(守约，守约)和双方同时选择不守约(违约，违约)。而只有双方都选择守约的策略组合能够实现帕累托最优，维持长期的合作伙伴关系；而同时违约的策略会降低核心企业的信用水平，破坏核心企业与中小企业的合作，产生“囚徒困境”问题。

2)从动态演化博弈的视角来看，核心企业与中小企业根据对方的策略选择对自己最有利的策略，并不断适应调整。其中银行贷款利率、违约企业惩罚力度、供应链企业长期稳定合作产生额外收益对供应链企业的策略选择产生重要影响。

基于此，为了提高核心企业与中小企业选择守约策略的概率，可以从以下两个方面进行拓展：从银行的角度来说，银行是为企业贷款的主要承担者，应该扮演积极的治理角色，通过适度降低贷款利率吸引核心企业贷款，提高对违约企业的惩罚力度，规范供应链企业；从供应链行业来说，积极引入区块链技术，解决传统供应链金融由于“信息孤岛”产生的信息不对称问题，从而规避了金融市场的道德风险问题，提高供应链企业长期稳定合作产生的额外收益，营造良好的金融生态环境，促进供应链金融企业的发展。