基于GLUE 方法的湖库富营养化风险评估

郑 震

（福州市环境科学研究院，福州 350000）

0 引 言

【研究意义】富营养化是指水体中氮、磷等植物生长所必要的元素大量增加，使得水体生态系统生产力（光合作用效率）增加的现象[1]。自然状态下，湖泊等水体的水生态系统处于相对平衡的状态，富营养化进程往往需要百年甚至更久。相反，受到人类活动影响的湖库等水体，存在大量外源性营养盐（N、P等）的输入及人为影响水体流域下垫面及水体本身水动力特性的现象，从而加速了湖库富营养化转变的进程[2]。湖库作为重要的淡水资源，承担着生活用水、工业需水、农业灌溉用水、水产养殖用水等很多重要的水体功能[3-4]，其富营养化问题引起藻类大量繁殖，大量消耗水体溶解氧，经常造成区域水体“死区”，引起水体发臭，破坏固有的生态系统。因此，如何科学评估及防治湖库富营养化问题尤为重要。【研究进展】国内外学者对湖库富营养化水平评估、营养盐影响机制、时空分布、水生态系统N、P、C 等元素循环、富营养化数值模型等方面做了大量研究工作[5]，其中，将湖库富营养化水平的合理评估作为治理的基础尤为重要。1977 年，卡尔森[6]首先提出以透明度为参考基准的富营养化指数（TSI）用以评估水体富营养化状态，随后，不同学者在此基础上提出了不同类型的评估体系，如修正的卡尔森指数法、评分法、生物指标法及综合营养指数法等[7]。【切入点】虽然评估方法多，但大都是一种确定性评估指标体系，如营养指数法，其本质是以透明度或叶绿素为基准评价因子，其他评价因子则通过与基准评价因子间寻求线性关系构建的确定性数理方程。这些方法虽然可以简单快速计算出富营养化相关指标的评估值，但每个湖库有其自身的富营养机制特性，且评估的富营养相关评价因子之间在实际分析中不一定会存在相关性[8]。故单纯定义某个确定性评估数值去判断水体富营养化状态难免会出现“误判”，确定性指标计算出的贫营养状态下也有可能会引发水华现象。【拟解决的关键问题】故提出将水体富营养化视为一个多参数输入、以叶绿素质量浓度作为表征水体富营养化输出的概念模型。采取处理复杂系统的BP 神经网络进行构建富营养模型，利用基于贝叶斯理论的“GLUE”方法，通过其模型参数的不确定性分析得出模型参数的富营养化范围及不同参数的富营养化敏感性。从而为湖库富营养化管理给出不同富营养化相关水质指标的调控范围，有利于对湖库富营养化进行监控预警、分类防治。

1 材料和方法

1.1 研究区概况

山仔水库位于敖江中游，下垫面为山地丘陵，经纬度坐标为26°17'51″N、119°21'35″E，水库控制流域面积1 646 km2，调节库容1.064 亿m3，多年平均来水量18.59 亿m3，多年平均气温为19 ℃。库区形态为入库河流狭长中间宽深的不规则水库，多年平均水深约30 m，流速分布差别较大，库区狭长水道流速较快，库区中心较慢。流域内污染源包括居民生活污染源、农业种植及零散畜禽养殖等。库区藻类分布以蓝藻为主，自2000 年起，山仔库区部分区域出现“水华”现象[9]。

1.2 数据选取

福州市环境监测中心站于2011 年6 月—2015 年12 月在山仔水库库区均匀布设5 个监测点（皇帝洞、七里进口、库心、日溪进口、坝下；图1）监测库区水质，频率为每月上下旬各1 次。

图1 研究区概况 Fig.1 Study area

对数据整理后得到190 组监测数据开展后续研究，水质指标包括水温（T）、pH、溶解氧（DO）、透明度（SD）、高锰酸盐指数（CODMn）、总氮（TN）、总磷（TP）、叶绿素a（Chl-a）。

1.3 原理和方法

1.3.1 BP 神经网络

BP 神经网络是基于生物神经元传递信息的原理，将信息传递过程划分为输入层、隐含层及输出层3 部分[10]。通过输入一定数量样本的训练组，对训练结果与实际输出值直接的总体误差函数反向层层求导，逐步逼近总体误差最小值，在给定的训练次数下，最终得出符合误差训练阈值的特定神经网络。

BP 神经网络基于生物神经传播，机理较为清晰，但关于隐含层层数及隐含层节点个数准确确定上仍存在较大争议。太少的隐含层节点数不足以区分较为复杂的输入—输出结构，而太多节点数则容易造成“过拟合”现象，训练集表现很好，而验证集则表现很差。目前较为认可的方法是根据经验公式n1=√n+m+a（n1为隐含层节点数；n为输入层节点数；m为输出层节点数；a为1～10 的整数）得到的范围进行试算，以得到最佳节点数[11]。本文构建的BP 神经网络富营养化模型中8 个水质参数作为输入层，叶绿素浓度作为1 个输出层。根据经验公式，隐含层的节点范围区间为[4,13]，利用“穷举法”得出区间内最优训练方案的节点数，得出最优模型。

1.3.2 GLUE 方法

作为Bayes 统计推理的一种方法，GLUE 方法的特点是放宽了似然函数的统计学条件[12]。其认为某个模型结果是基于模型本身多个参数的共同驱动，而不是单个参数。基本思路为：确定似然函数并设定似然阈值，得到有效参数值，然后对参数进行数据统计分析,似然函数的确定主要依据2 个原则：①具备判别模型的好坏程度的能力。②单调递增函数（即似然值越大，表示模型越能表达模拟效果）[13]。本文将水体富营养化考虑为多参数（水温、pH、溶解氧、透明度、总氮、总磷、当前叶绿素a 质量浓度等）的评估未来叶绿素质量浓度变化的预测模型。假设以水体富营养化程度爆发水华风险的可能性作为评价模型好坏的标准。选取BP 神经网络富营养化模型中8 个水质参数，利用Matlab 均匀分布生成器，随机生成10 000组8 维向量组，通过BP 神经网络模型做出预测。

叶绿素质量浓度与富营养化（水华风险性）程度有着极强的指示性。采用以叶绿素质量浓度为基准的卡尔森指数表达水体富营养化程度具有较大的可靠性[14]，故本文采用叶绿素卡尔森营养指数（TSI）作为似然函数进行评价。为遵从似然函数的2 个原则，对基于卡尔森营养指数做进一步标准化，使得得到的似然函数值处于[0，1]区间，越接近1，表示预测的叶绿素质量浓度越高，爆发水华的风险可能性越大。计算似然函数见式（1）、式（2）。

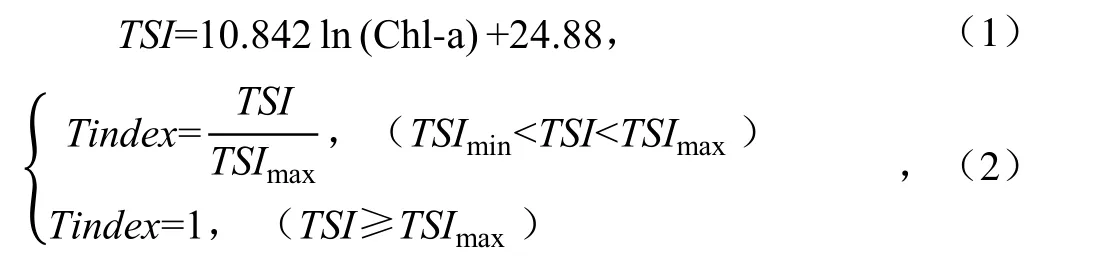
式中：Chl-a 为叶绿素a 质量浓度（μg/L）；TSI为叶绿素卡尔森综合指数；Tindex为标准化似然数，范围为[0，1]；TSImin为卡尔森营养指数评估指数下限值（基于待评估湖库专家经验的人为指定值，小于此值表示产生水华风险性）；TSImax为卡尔森营养指数评估指数上限值（基于待评估湖库专家经验的人为指定值，大于此值表示产生水华风险性）。

本文基于库区多年监测评估，参考中国环境科学研究院霍守亮[15]提出的山区湖库分级标准，取Ⅳ级中度富营养中叶绿素质量浓度均值112 μg/L，定义为库区水华风险富营养模型上限值，即似然值为1，认为必然爆发水华。取Ⅲ级轻度富营养中叶绿素质量浓度均值18 μg/L 作为发生水华风险的下限值，即似然值为0，认为叶绿素高于此质量浓度时，开始具有水华爆发的风险。

本文基于GLUE 方法的具体研究步骤为[16]：①均匀取样10 000 组参数组，通过BP 神经网络计算叶绿素质量浓度为基准的卡尔森指数。一般数学模型不确定性的分析研究中，由于参数的未知性，其先验分布多假设为某一合理分布区间内的均匀分布。②筛选似然值大于0.3 的参数组（认为0.3 以上即存在较大水华风险）作为有效参数组进行评估。③根据本文提出的标准化似然函数公式计算参数组的似然函数值。④将各参数似然函数值进行归一化，确保总和为1，得到各参数概率密度分布函数及累计概率分布函数，并得出水华发生较高风险的参数评估置信区间（本文取90%置信水平）。

表1 叶绿素a 标准分级 Table 1 Chlorophyll-a standard classification

表2 参数初始值范围 Table 2 Parameter initial value range

2 结果与分析

2.1 BP 模型适用性评估

通过Matlab 软件中的BP 神经网络工具箱，输入190 组实测数据集，以自动训练生成net 模型，为了进一步验证评估模型的适用性与稳定性，随机取3 组[100，90]数据集（100 组为验证集，90 组作为校核集），计算纳什（NSE）系数及均方根误差（RMSE）指标对模型进行评估，同时试算最优隐含层节点数与隐含层数，最终确定BP 模型构型为8-8-5-1（输入层为8；隐含层2 层，分别8 个神经元、5 个神经元，输出层为1），详细结果见表2。由表2 可知，模型验证集NSE系数均值为0.66，RMSE为7.56；校核集均值为0.63，RMSE为7.09。NSE系数越接近1，表示模型模拟表现越好，一般水文水质模型预测中，由于人类本身对自然现象模拟认知的模糊性及自然界水文水质现象普遍存在“噪声”干扰（如人为监测数据的误差、各种自然界中无法估计的偶发性等），很难得到一个很准确的模拟，参考相关研究文献[17]，一般认为0.5～0.65 之间即可认为可以接受。RMSE精度需根据统计数据的量级进行判断是否合理，通过190 组数据集训练得到的BP 神经网络模型，模拟得到的叶绿素浓度在基本上在100 以内，均方根误差在10 以内，即存在低于10%的误差，在可接受范围。故构建模型适用性较好，可用来进行数值实验，分析各参数的不确定性。

表3 模型评估 Table 3 Model evaluation

2.2 水质参数的不确定性分析

根据本文给出的似然函数公式计算出参数组的似然值，筛选得出各个水质参数大于0.3 的似然值，并绘制成相应的散点图，见图2。点状图是参数值相对于似然值的散点图。每个点代表使用许多随机选择不同的参数值的蒙特卡罗实验模型的1 次运行。可以看出不同水质参数的不同区域分布特征，它们本质上表示采样点从拟合响应面到单个参数维度上的投影，投影特征代表了每个水质参数发生水华风险时候的偏好范围。对于每个参数，其较高风险（靠近顶部）或较低风险（靠近底部）的点的分布可以覆盖到整个参数采样范围。同样的，不同的参数存在不同的风险特征区间，例如pH 值、CODMn、TN、TP、Chl-a、SSD 的高、低风险特征在区间内表现较为明显；T、DO 的风险特征则不明显。

pH 值、DO、CODMn、TN、TP、Chl-a 与水华风险有着较为明显的正相关趋势，SSD 则存在负相关趋势，T集合风险分布较为均匀。符合实际情景下，叶绿素质量浓度越高、透明度越低，藻类越多；营养盐、氮、磷作为供给藻类生长的“食物”，可促进藻类生长，提高发生水华的风险。对仔水库的研究表明，TP为其限制性营养盐，TN 为非限制性营养盐[18]，此次TP 散点图并未能很好地反映非限制性营养盐的区间特征，即TN 对藻类的影响在一定的范围内，超过影响范围后，TN 对藻类的影响不会发生太大变化。可能由于总氮取值区间（右）值太小，并未覆盖到影响失效的范围或BP 模型比较依赖训练集，对超出训练集范围的参数集合，不能很好地反映。

一个模型给出的风险好坏并不仅由单个参数决定，而是整个参数集合参数之间相互作用的结果[19]。点状图作为响应曲面的投影，不能完整地反映反映曲面形状的复杂参数相互作用的结构。某种意义上，本研究主要关心风险高的参数集合是什么，故对筛选后的有效参数组分别计算其概率密度函数及累计函数，得出不同水质指标参数90%置信区间，具体结果参见表3。即当水质参数落在此分布区间内，即存在较高的水华风险，需要管理部门警觉。

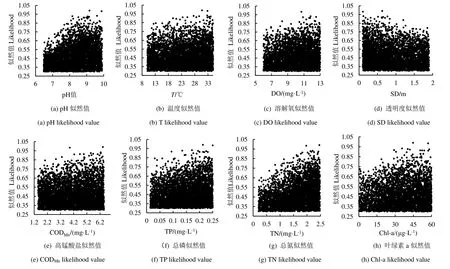
图2 参数似然值散点图 Fig.2 The prior distribution histogram and probability cumulative curve of test parameters

表4 模型评估区间 Table 4 Model evaluation interval

3 讨 论

由于水文、水质模拟存在较大的复杂性、模糊性及随机性，模拟精度尚需进一步提升，如比较常用水质模型上AnnAGNPS、SWAT、HSPF 等[20]，而BP神经网络模型在预测精度上也并没有较为明显的改善，故在评估水华风险上仍需要展望未来水文、水质模型的研究中提出更好的模型架构与数值方法，以期预测精度可以有明显提升，进而进一步提升水华风险评估精度。另一方面，采样方法上本文采取的简单均匀取样操作简单，但必须依靠大量样本，才能保证高维分布取样的有效性[21]。目前MCMC、超拉丁取样方法在估计多参数的后验分布方面优势较为明显，即与GLUE 方法相比，其利用比较小的样本集合即可得到模型参数的后验分布过程[22]。此外，人为判断的水华风险的“有效似然值”判断标准并不统一，依赖不同地区不同人的经验判断，带有一定的主观性[23]，故未来需要进一步尝试与探索。

4 结 论

1）在给定足够多样本训练下，可基于多参数响应机制和BP 神经网络建立水库藻类及其他类似复杂机制系统的模拟。

2）评估得到发生水华风险的模型参数90%置信区间，可作为库区水华风险管理的预警控制区。