被动多传感器空时联合检测前跟踪方法

宋科康,杨宇翔,刘成元

(盲信号处理国家级重点实验室， 成都 610041)

利用被动传感器对舰船和飞机等目标辐射的信号进行探测和定位具有隐蔽性高、成本低等优点，受到广泛关注。而如何通过被动传感器对目标自身辐射的微弱信号进行检测一直是信号处理领域中的研究热点[1-2]。被动传感器缺乏发射信号的先验信息，当接收信号微弱时，仅采用单一传感器难以发现目标，因此常常采用多个传感器联合探测。传统的多传感器联合检测思路是：各个传感器根据各自检测阈值进行独立检测，然后将检测结果传输到处理中心，再依据融合判决准则进行联合处理。该类方法分两步处理使得实现过程简单，但存在信息损失。随着光纤传输与计算能力的发展，将各传感器原始信号传输到处理中心进行空时联合积累检测成为可能。其中，多传感器联合的检测前跟踪(Track- Before-Detect,TBD)方法就是一种有效的空时联合积累检测方法。TBD方法将检测与跟踪进行一体化处理，不对单帧数据进行检测，而是对多帧数据先积累后检测，同时实现目标的检测与跟踪。国内外学者对TBD算法进行了较多研究，包括霍夫变换的检测前跟踪算法(Hough Transform TBD,HT-TBD)[3]、动态规划的检测前跟踪算法(Dynamic programming TBD,DP-TBD)[4]、粒子滤波的检测前跟踪算法(Particle Filter TBD，PF-TBD)[5]等。动态规划的检测前跟踪算法易于实现，受到广大学者的青睐。文献[6]中在机载早期预警雷达中基于运动目标DP-TBD方法，提出一种低复杂度的计算方法；文献[7]中将该方法推广到空时自适应处理雷达；文献[8-9]中为提高算法实时性，降低复杂度，提出两步多帧检测框架，提高了计算性能。文献[10]中引入状态转移概率进行改进，提高了目标检测和跟踪性能。此外，针对多帧积累中滑窗处理的多次重复计算问题，文献[11]中对滑窗处理进行改进，降低了计算量。上述文献主要是针对单一传感器在时延-多普勒平面上进行检测的，如何实现多传感器的联合检测前跟踪尤其是空时联合检测前跟踪是值得研究的问题[12]。因此，本论文探讨被动多传感器的空时联合检测前跟踪方法，理论推导多传感器联合的广义似然比，然后将该似然比作为积累值函数，并映射到位置-速度空间，再依据目标位置和速度相对各传感器的唯一性，实现各传感器接收信号能量在位置-速度空间的叠加，最后采用动态规划的检测前跟踪方法进行空时积累检测，大幅提高了目标检测概率。

1 被动多传感器系统模型

1.1 运动模型

不失一般性，假设目标在二维平面内进行匀速运动，则目标状态方程可表示为

yk+1=Wyk+vk

(1)

(2)

其中，T为每帧信号的时长。

1.2 信号模型

(3)

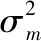
(4)

(5)

其中，λ为波长。

xm=ηmDmu+wm

(6)

(7)

H(z)=diag([e-j2π(0)z,e-j2π(1)z,…,e-j2π(N-1)z])

(8)

随着时间推移，目标状态在发生改变，为实现空时联合积累，将各站接收信号进行时域分段处理(每段时间较短)，每一段记为一帧，并且假设每帧内目标状态基本不变，并记每帧时长为T。则第k帧时，第m个传感器的观测方程为

xk,m=ηk,mDk,muk+wk,m

(9)

令xk=[(xk,1)T,…,(xk,M)T]T，则有观测方程为

(10)

(11)

其中，k=1,…,K。

2 动态规划的多传感器检测前跟踪方法

根据目标的运动模型和信号模型，首先推导多传感器的广义似然比，并将其作为值函数，然后采用动态规划的检测前跟踪方法实现多传感器联合的空时积累检测。

2.1 值函数选取

如何选取积累值函数是进行空时联合积累的关键，由于不同传感器对应的时延多普勒不同，使得在时延-多普勒图像中进行积累的方式失效。对此，本研究直接选取各传感器接收信号的广义似然比作为值函数，不进行中间参数转换，信息损失少，检测性能更佳。

在目标存在时，即H1假设下，由式(10)可得第k帧时，各传感器接收信号的联合概率密度函数为

(12)

在目标不存在时，即H0假设下，第k帧接收信号的联合概率密度函数为

(13)

根据式(12)和式(13)化简得对数似然比为

(14)

式(14)中存在未知参数ηk,m，其最大似然估计为

(15)

将式(15)代入式(14)中，则有

(16)

(17)

l(xk)=λmax(Gk)

(18)

根据矩阵Gk的定义可知，Gk的最大特征值表征接收信号的总体能量，实现的是第k帧时各传感器接收信号的空域积累。因此选取式(18)中最大特征值作为值函数是合理的，将其记为Q(yk)=λmax(Gk)(Gk是关于yk为变量的矩阵)。

2.2 位置-速度空间映射

(19)

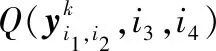
2.3 动态规划算法

根据积累值函数和位置-速度空间的映射，采用动态规划算法进行空时积累检测。分析第k-1帧和第k帧的积累值函数，假设在第k帧时寻找到最大值对应的状态单元为(q1,q2,q3,q4)，并以状态转移数等于4为例，则第k-1帧可能到达第k帧最大值处的状态区域为L4={q1-q3T-δ1,q2-q4T-δ2,q3-δ1,q4-δ2}，其中δ1=0,1，δ2=0,1。进一步，将第k帧时的积累值函数表示为Ik，则可得第k-1帧和第k帧的积累值函数递推关系式为

(20)

其中，h为相邻两帧之间可能的有效状态转移数。式(20)表明，第k帧的积累值函数Ik为当前时刻测量值Zk与上一时刻积累值函数Ik-1在k-1时刻对应所有可能变化范围内的最大值。同时，记录第k时刻得到的状态转移关系为

(21)

式(21)表示在可能的状态范围Lh内求取使积累值函数达到最大的状态，即在k-1时刻最有可能转移到yk的状态，故ψk记录了状态转移过程。

结合式(20)和式(21)，可将基于动态规划的被动多传感器空时联合检测前跟踪算法流程小结如下：

步骤2：令k=k+1，根据式(20)中的递推关系式计算第k帧的积累值函数Ik，并根据式(21)记录状态转移过程ψk。

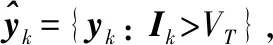
上述步骤3中检测阈值可采用蒙特卡罗计算，也可根据参考文献[4]进行近似计算。

3 仿真实验与分析

3.1 仿真条件

目标初始位置为[0,0] km，采用4个固定传感器接收目标辐射信号，传感器和目标初始位置如图1所示。图1中传感器坐标分别为[10,15] km,[-20,5] km,[-15,-15] km和[15,-5] km，目标初始位置为[0,0] km，速度为[200,200]m/s，在二维平面内沿东偏北45°方向匀速直线运动。目标发射信号为QPSK信号，基带带宽为20 kHz，复采样率为20 kHz。

图1 传感器与目标初始位置

观测位置范围[-2,-2] km到[2,2] km，位置分辨率单元为50 m×50 m，速度范围为[100,100]m/s到[300,300]m/s，速度分辨单元为20 m/s×20 m/s，信号时长共2.5 s，每帧时长0.25 s。

3.2 仿真实验

仿真实验1积累前和积累后值函数幅度在位置空间的分布图。

图2和图3中分别给出积累前第1帧和积累10帧时，积累值函数经幅度归一化后在位置空间的分布图(对应的速度为200 m/s时)。对比分析该两图，可以看出在第1帧时较难发现目标，而积累10帧后可以明显看到目标峰值。此外，图3中归一化后的积累效果图表明，积累后的噪声分布更加平坦，即噪声方差更小，而信号峰值不变，因此使得积累后的峰值信噪比明显增高。

图2 积累前第1帧位置空间三维图

图3 积累10帧后位置空间三维图

仿真实验2多传感器联合积累后检测概率变化对比。

图4中给出虚警概率10-3时，检测概率随积累帧数的变化曲线。分析图4可以看到，随着积累帧数的增加，目标检测概率明显提高，在第1帧时几乎无法发现目标，而积累10帧后的目标检测概率已经基本为1，这与图2和图3中分析的结论是一致的。

图4 检测概率随积累帧数变化曲线

仿真实验3多传感器联合积累后的位置估计误差对比。

图5给出本文方法与传统方法在50次蒙特卡罗仿真下位置估计误差曲线，其中传统方法1是指采用单帧位置估计的方法，传统方法2是指将每次积累后的值函数直接用于位置估计的方法。图5中结果表明本文方法位置估计误差最低。传统方法1的估计结果说明直接进行单帧估计误差很大，而传统方法2的估计结果表明直接将积累后的方法进行位置估计而不进行回溯估计会降低初始帧的估计精度。

图5 位置估计误差随积累帧数变化曲线

4 结论

本文提出信号层输入的被动多传感器空时积累检测方法。该方法将多个被动传感器接收信号的广义似然比作为积累值函数，并将其投影到位置-速度空间进行空域积累，接着采用动态规划的检测前跟踪算法实现空时积累检测。仿真实验表明本文方法具有较好的目标检测性能和位置估计精度。由于位置-速度空间运算量较大，因此如何利用先验信息和快速算法实现更加高效的计算是下一步需要研究的重点。