章丘全民健身中心健身馆结构设计与分析
韩振林,张继合
(山东省建筑设计研究院有限公司,山东 济南250000)
0 引言
现代空间结构在各种体育场馆、剧院、会展中心、机场候机楼、工业厂房等建筑中得到迅速发展和广泛应用,同时空间结构技术也被誉为一个国家建筑业水平的象征。空间结构是指结构形体呈三维形状,具有三维受力特征并呈空间工作的结构。与平面结构不同,空间结构不仅仅依赖材料的性能,更依赖自己合理的形体以充分利用不同材料的特性[1]。按组成空间结构的基本单元分类,即板壳单元、梁单元、杆单元3种刚性单元及索单元、膜单元两种柔性单元;而按现代空间结构可分为现代刚性空间结构、现代柔性空间结构和现代刚柔性组合空间结构3大类[2]。
体育馆建筑由于对大空间的天然需求,成为空间结构应用的理想场所。一般体育馆建筑是由屋盖、立面墙体等围合而成的闭合空间结构,屋盖的主要组成部分可分为:主承力结构、支撑体系、支座等。主承力结构主要承受竖向荷载、支撑体系和边缘构件,对结构的面内刚度和整体稳定性有较大贡献[3]。在20世纪80、90年代,限于当时的设计和施工水平,体育馆建筑屋面以网架和网壳为主要结构形式,如首都体育馆的平面尺寸为99 m×112.2 m,为我国矩形面平面屋盖中跨度最大的网架;上海体育馆的平面为圆形,其直径为110m、挑檐为7.5m,是目前我国跨度最大的网架结构。1994年建成的天津新体育馆,其平面为圆形,直径为108 m、挑檐为13.5m、总直径达到135m,曾是我国圆形平面跨度最大的球面网壳[4]。近年来,随着社会经济技术水平的不断提高,尤其随着计算机分析能力的飞跃式发展,对钢结构稳定理论研究的不断深入,提高了钢结构加工和施工水平,一大批新型空间结构应用于体育馆结构,如空间立体桁架结构、拱支网壳结构、张弦梁结构、弦支网壳结构等,涌现出一批造型新颖、技术先进的优秀工程案例。其中,空间立体桁架属于刚性空间结构,一般由上下弦杆和斜腹杆组成,弦杆和腹杆多采用圆钢管,节点采用相贯焊接;由于空间立体桁架整体稳定性好、施工质量容易控制且外形简洁有力,成为中型体育馆中应用最为常见的结构形式之一[5]。
文章结合章丘全民健身中心健身馆的实际工程,对主体结构设计和钢结构屋盖的整体稳定进行研究,并介绍了超长混凝土结构在温度作用下的应力分布,且针对体育馆建筑中常见的大跨度楼盖进行了楼盖舒适度分析,其相关研究成果可为类似项目提供参考和借鉴。
1 工程概况
章丘全民健身中心健身馆位于济南市章丘区,主要满足市民日常健身需求,内设健身、篮球、羽毛球、乒乓球等场管,为无看台的体育馆建筑。健身馆平面为圆形,外围直径为96 m、建筑面积为18 000 m2、建筑高度为32.5 m。地上三层,局部为地下一层,地下一层层高为5.4m,地上一、二层层高均为5.1 m、三层层高为3.9 m。健身馆主体结构采用框架剪力墙结构,一般柱距为7.5m×9m和7.5m×15 m,局部大跨度柱距为7.5 m×29.7 m。屋面采用空间钢结构,由16榀径向拱形桁架组成,拱形桁架跨度为78 m、矢高为14.23 m,采用倒三角形立体桁架,桁架高度和宽度皆为3 m;沿屋面环向设置了4道腰桁架以保证径向拱形桁架的稳定性;基础采用人工挖孔桩。
健身馆结构具有如下特点:(1)钢结构屋盖跨度大,需对屋盖的稳定性能进行研究;(2)外围直径达96 m,远超出GB 50010—2010《混凝土结构设计规范》[6]所规定的伸缩缝的最大间距限值;(3)三层29.7 m中大跨楼盖使用功能为篮球场,楼盖频率和竖向加速度的控制直接影响使用者的舒适度体验[7]。
项目效果图如图1所示,典型平面和剖面图如图2、3所示。

图1 健身馆建筑效果图

图2 健身馆平面图/mm

图3 健身馆剖面图/m
2 章丘全民健身中心健身馆结构设计
2.1 结构设计标准及荷载
2.1.1 结构设计标准
根据健身馆的使用功能和重要性,确定建筑物安全等级为二级,结构设计使用年限为50年,其重要性系数有:上部钢屋盖为1.1、下部混凝土结构为1.0。基础设计等级为乙级、抗震设防类别为丙类、抗震设防烈度为7度、设计基本地震加速度为0.10g、地震分组为第三组、场地类别为Ⅱ类、场地特征周期Tg=0.45 s,框架和剪力墙抗震等级为二级。设计中采用的地震动参数见表1[8]。

表1 地震动参数表
2.1.2 荷载
(1)恒荷载与活荷载
结构构件自重由程序自动计算,考虑钢构件的连接节点和焊缝重量,杆件重量按实际重量的1.1倍取值,屋面恒荷载、活荷载及屋盖吊挂荷载分别取1.0、0.50和0.50 kN/m2,基本雪压为0.35 kN/m2(重现期100年)。
(2)风荷载
重现期50年的基本风压Wo为0.45 kN/m2、屋盖钢结构计算按重现期100年的基本风压Wo为0.50 kN/m2、地面粗糙度类别为B类,体型系数根据GB 50009—2012《建筑结构荷载规范》[9]选择。
(3)温度荷载
工程外围直径为96m,超出GB 50010—2010[6]所规定的伸缩缝最大间距限值,应考虑温度荷载作用对主体和屋盖结构的影响。
由GB 50009—2012[9]可知,济南地区基本气温最低为-9℃,最高为36℃。根据工程预计施工进度安排,结构合拢温度定为15~20℃。参考文献[10]进行各区域温差计算,计算结果如下:室内混凝土结构最大温升为4℃、最大温降为-20℃;室内钢结构最大温升为14℃、最大温降为-20.4℃;室外混凝土结构最大温升为16℃、最大温降为-29℃;室外钢结构最大温升为29℃、最大温降为-28℃。
2.2 主体结构设计
健身馆为按7度设防的丙类高层建筑,主体结构采用框架剪力墙结构,剪力墙结合楼梯间在周边布置以增大结构的抗扭性能;其二层局部楼板抽空、三层为篮球场,而四层仅设置局部夹层。三层大跨度区域采用部分有粘结预应力梁,梁最大跨度为29.7 m,预应力梁采用单向布置,间距为3.5 m,梁截面为500 mm×1 800 mm,预应力筋在大跨及两端相邻跨布置;预应力筋采用1 860级高强低松弛钢绞线,为保证预应力梁的延性,采用预应力筋与热轧钢筋HRB400混合配筋的形式,按配筋强度比定义的预应力度控制<0.75,且控制支座处梁截面受压区高度<0.35。考虑到工程存在较大范围的楼板抽空、层间夹层、跃层柱及大跨度框架等抗震不利因素,框架和剪力墙的抗震等级均取二级。设计中参照JGJ 3—2010《高层建筑混凝土结构技术规程》[11]中抗震性能目标C级进行了抗震性能化设计,将支承大跨梁的框架柱、支撑屋面拱形桁架的框架柱、跃层柱及底部剪力墙定义为关键构件。
屋面主要承重体系由16榀拱形桁架径向交叉组成,拱形桁架采用倒三角立体桁架,其跨度为78 m、矢高为14.23 m,周边支座均为定型金属固定铰支座;沿环向设置4道腰桁架以保证拱形桁架的稳定性,腰桁架也采用倒三角立体桁架,两上弦杆间距与拱形桁架腹杆节间尺寸相对应;桁架杆件均采用Q345B圆钢管,节点为相贯焊接;为保证屋盖结构整体性,桁架上弦之间布置屋面水平支撑。各层及屋面结构布置图如图4所示,其杆件截面见表2。

图4 各层楼面及屋面结构布置图

表2 杆件截面表/(mm×mm)
3 章丘全民健身中心健身馆结构计算分析
文献[12-13]对上、下部刚度相差较大的结构进行动力性能分析,其结果表明:下部混凝土结构对上部钢屋盖的影响较为有限,整体计算模型的振型主要表现为钢屋盖的振动,并与单独考虑钢屋盖模型时的振型及分布情况较为接近,因此可单独取上部钢屋盖结构为对象进行分析。鉴于工程的重要性,此工程采用钢结构有限元软件3D3S(V11.1)对上部钢屋盖独立模型进行分析,采用通用有限元软件Midas Gen进行钢屋盖整体稳定性分析。对钢屋盖的计算分析考虑了恒荷载、活荷载、风荷载、温度荷载及地震作用的组合;恒荷载、活荷载和风荷载由程序自动导算到节点;并考虑了马道、灯具、设备等吊挂荷载。桁架上、下弦杆连续贯通,腹杆与弦杆节点分别设置为刚接点和铰接点,杆件内力值取二者的包络值。
钢桁架跨中挠度控制值为L/250(L为桁架跨度);屋盖竖向自振频率≥1.0 Hz;主桁架上、下弦杆靠近支座处四个节间的杆件长细比≤120;多遇地震作用下杆件最大应力比≤0.8,主桁架弦杆和支座附近腹杆的应力比≤0.75;中震弹性计算时杆件应力比≤0.9;考虑初始缺陷分布的几何非线性整体稳定分析,屈曲荷载系数≤4.2。
采用有限元软件盈建科(YJK)建立下部混凝土结构和屋面钢结构的整体模型,进行多遇地震作用下的计算分析、关键构件的中震弹性、中震不屈服和大震不屈服验算以及主体结构的温度应力分析,对大跨楼盖区域采用Midas Gen软件进行楼盖舒适度验算。水平地震作用下的计算采用考虑扭转耦联振动影响的振型分解法,并考虑偶然偏心和双向地震的影响,对钢屋盖采用振型分解法进行竖向地震作用计算。钢屋盖单独计算模型及总体计算模型如图5所示。

图5 钢屋盖单独及总体计算模型图
3.1 钢屋盖计算
3.1.1 内力分析
屋面钢屋盖外形为半球形曲面形状,风荷载体型系数按照GB 50009—2012[9]取值,风荷载由程序自动导算到节点上,均为风吸力。风吸力作用下验算杆件内力时恒荷载为有利荷载,且其分项系数取1.0,风载和恒载的荷载组合设计值S为1.0恒+1.4风;风吸力作用下钢屋盖桁架跨中最大挠度为5.0mm(向下),风吸力荷载组合下未出现支座受拉的情况。
在各种工况组合下,主桁架上下弦杆受力以轴向压力为主,在恒荷载、活荷载和温度荷载组合下,压力最大值出现在靠近支座处的下弦杆,其值为1 180 kN;桁架腹杆受力有拉有压,压力最大值同样出现在支座处的腹杆,其值为175 kN;屋面中心设置的环形立体压环的弦杆受力较大,轴压力最大值为910 kN;对Midas Gen和3D3S软件的计算结果进行比较,两者差值<1%,可见计算结果真实可信。桁架杆件应力分布图如图6所示。

图6 屋盖最不利内力分布图
根据图6分析可知,屋盖独立模型中拱形桁架对支座的径向水平推力最大值为412 kN,对应的荷载组合为1.2恒+1.4活+1.4×0.6温降;整体模型中水平推力最大值为325 kN,与独立模型对应的荷载组合相同,与独立模型的水平推力相差21%,这是由于整体模型考虑了下部刚度,对屋盖的约束程度有所削弱,整体模型更能反映实际情况,因此实际设计中支撑桁架的框架柱配筋以整体模型计算结果为基础进行适当加强。
3.1.2 竖向挠度
在恒载+活载的标准组合下,屋盖跨中竖向挠度最大值为31.737(3D3S)和30.753 mm(Midas Gen);两软件计算结果的差值<3.1%,远小于JGJ 7—2010《空间网格结构技术规程》[14]中所规定的跨度1/250的限值要求,可见拱形屋面有极大的面外刚度。竖向挠度结果如图7所示。

图7 屋盖挠度有限元计算结果图
3.1.3 动力特性
钢结构屋面振动模态密集,分析时计算了独立模型200阶振型,x、y、z各方向质量参与系数均>90%,第1、2、3和4前4阶振型对应的周期分别为0.49028、0.48869、0.41065和0.39775 s,其振型图如图8所示。
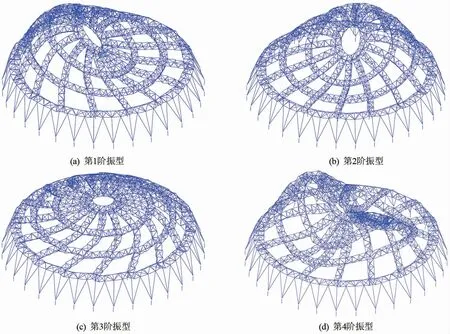
图8 独立模型前4阶振型图
3.1.4 杆件应力比
桁架杆件截面尺寸基本为长细比要求控制,少部分杆件截面尺寸由强度控制,大多数杆件应力比<0.7,杆件最大应力比<0.8,主桁架弦杆和支座附近腹杆的应力比<0.75,满足预定的应力比控制目标,限于篇幅不再列出。
3.2 屋盖整体稳定性分析
立体桁架的失稳按分析方法可分为线性屈曲和非线性屈曲,线性屈曲也称为特征值屈曲;按照其平衡路径又可分为分支点失稳、极值点失稳和跃越失稳;按照失稳后结构是否发生出平面变位又可分为平面内失稳和平面外失稳[15]。该工程径向拱形桁架的平面外稳定性由腰桁架和屋面水平支撑保证。利用Midas Gen有限元软件,将特征值屈曲与弧长法结合,分析结构非线性屈曲问题,得到结构变形的失稳全过程,通过结构的荷载—位移全过程分析来考察屋盖稳定性能的基本规律。
3.2.1 特征值屈曲分析
首先对钢结构屋面进行了特征值屈曲分析,屈曲分析考虑的荷载组合包括1.0恒荷载+1.0全跨活荷载(工况1)和1.0恒荷载+1.0半跨活荷载(工况2)两种工况。工况1、2的前4阶振型屈曲特征值见表3。两种工况的前4阶模态失稳均为主桁架失稳,半跨活载分布下的屈曲特征值略小于满跨活载分布下的屈曲特征值,但两者仅相差约7%,表明以立体桁架为主要承重体系的空间结构的整体稳定性能对活载分布不敏感。
3.2.2 考虑几何非线性稳定分析
特征值屈曲分析得到的特征值可视为整体稳定的上限值,在特征值屈曲分析的基础上,考虑几何非线性,假定材料为完全弹性,通过施加初始几何缺陷,对钢屋盖进行整体稳定性分析。初始几何缺陷采用一致缺陷模态方法,选择模型的1阶屈曲模态的屈曲向量作为结构初始缺陷分布模式,按比例修正节点坐标,结构初始缺陷峰值参照JGJ 7—2010[14],按主桁架跨度的1/300,即260 mm取值。几何非线性稳定分析方法采用荷载—位移全过程跟踪分析,考察第1阶屈曲中位移最大点的荷载—位移情况,计算结果表明,考虑几何非线性后的荷载屈曲系数为8.0,大于规程最小限值4.20,表明屋盖结构刚度较大,整体稳定性能良好。
3.3 整体模型计算
采用盈建科(YJK)软件建立下部混凝土和上部钢屋盖的整体模型进行计算;振型数量为30,各方向质量参与系数均>90%,分析结果显示前4阶振型均为屋盖振动,与独立模型的模态周期对比见表4,振型图如图9所示。

表3 钢结构屋面前4阶振型屈曲特征值表

表4 整体与与独立模型的模态周期对比表/s

图9 整体模型前4阶振型图
对比图8、9可知,整体模型前4阶振型模态与独立模型中前4阶振型模态基本相似,但振型周期有所加长,可见考虑下部结构刚度后,屋盖的整体刚度有所减小;目前可考虑上、下结构共同作用的有限元软件功能已很完善,盈建科有限元软件采用了振型阻尼法计算,基于应变能因子,可根据不同材料的参与影响,得到符合实际的阻尼比,从而合理的考虑钢屋盖与下部主体的共同工作。同时,工程采用整体模型进行了多遇地震的抗震计算分析,对大跨度梁及钢屋盖进行竖向地震作用计算,各项整体指标和构件内力均满足规范要求,限于篇幅不再赘述。
3.4 楼板温度应力分析
根据上述计算出的不同区域温差,输入盈建科有限元程序进行温度应力分析。结果表明:在升温和降温工况下,各层楼板不同区域均出现拉应力和压应力,最大拉应力出现在降温工况下首层室外平台与室内柱子交界处,拉应力最大值为2.5 MPa。最大压应力出现在首层剪力墙附近,压应力最大值为1.1 MPa。升温工况下,楼板最大拉应力出现在首层剪力墙附近,最大拉应力为1.3 MPa。从下往上各层混凝土构件温度应力逐层减小;施工图配筋时应根据温度应力分布设置温度钢筋以防止楼板开裂。首层楼板应力云图如图10所示。
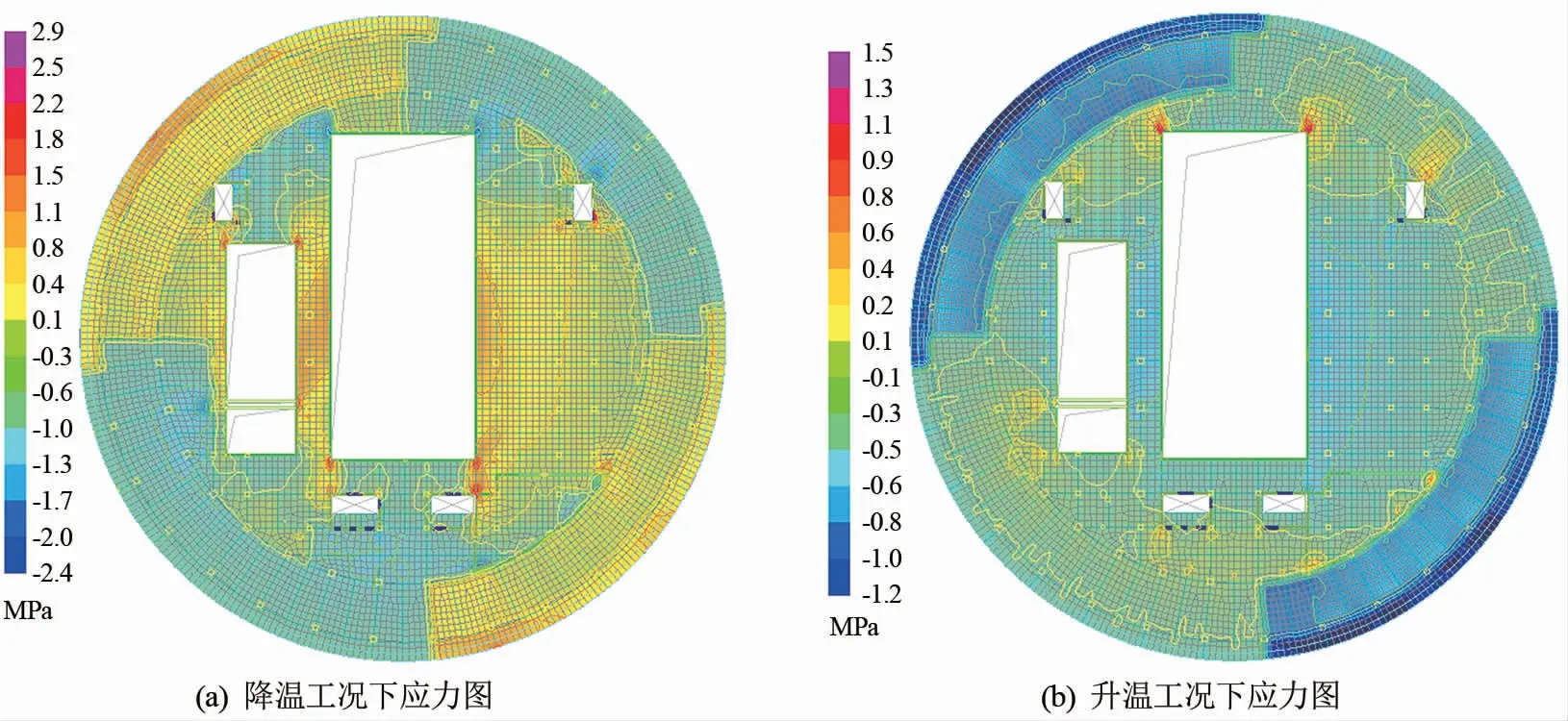
图10 升降温工况下首层楼板应力图
3.5 楼盖舒适度计算分析
工程三层大跨预应力梁布置区域跨度达29.7 m,功能为篮球场。根据规范GB 50010—2010[6]要求,应根据使用功能的要求进行竖向自振频率验算,并符合下列要求:大跨度公共建筑不宜<3 Hz;峰 值 加 速 度≤0.15 m/s2;同 时 根 据JGJT 441—2019《建筑楼盖结构振动舒适度技术规程》[16]规定,有节奏运动为主的楼盖结构,在正常使用时楼盖的第1阶竖向振动频率不宜<4 Hz。
采用有限元软件Midas Gen进行楼盖动力特性分析,截取第三层结构,梁、柱采用框架单元模拟,楼面板采用壳单元模拟。进行结构模态分析时,质量源选取恒载+楼盖自重,振动方向为垂直楼板的z方向。由于楼盖为混凝土结构,阻尼比取0.05。统计前12阶振型的周期、频率及质量参与系数见表5。大跨度楼盖第1阶振型图如图11所示。

表5 楼板前12阶振型周期及其参与系数表
大跨度楼盖第一阶频率为3.3375 Hz,满足GB 50010—2010[6]要求,但不符合 JGJT 441—2019[16]不宜<4 Hz规定。根据该工程的实际特点,可考虑采用单点TMD-粘滞流体阻尼器消能减振系统。经过优化计算,在大跨楼板结构跨中部位布置20套TMD减振装置,每套减振装置由粘滞阻尼器和调频质量阻尼器组成,包括弹簧减振器、粘滞阻尼器,质量块质量为650 kg,调频频率为3.2 Hz。荷载施加模式除均布荷载外,还考虑了跨中位置施加集中荷载的情况,加载区域布置图如12所示。
根据上述定义的加载模式,应用模拟的荷载曲线,进行人行荷载激励下的动力响应分析,3层楼板最大加速度峰值和减振率统计见表6。

图11 大跨度楼盖第1阶振型图

图12 大跨度楼盖加载区域布置图

表6 各加载模式下加速度峰值表
由表6可知,采用TMD减振技术可以大幅度降低楼板加速度峰值。在设计中预留设置TMD条件,在主体结构完工后组织试验检测,如楼板频率和竖向加速度无法满足技术标准要求,可增设TMD以满足舒适度要求。
4 结论
通过对章丘全民健身中心健身馆设计中关键问题的研究分析,可得到如下结论:
(1)屋盖独立和整体两种模型的屋盖振型模态接近,但考虑下部结构刚度后,屋盖的整体刚度有所减小,在一定程度会影响屋面杆件的内力分布;设计时可采用整体模型进行设计,对关键杆件可采用两种模型包络设计。
(2)考虑初始缺陷分布的几何非线性稳定分析得到的屈曲因子为8.0,满足规范最小限值4.2的要求,表明屋盖稳定性能良好。半跨活载分布下的屈曲特征值与满跨活载分布下的屈曲特征值相差仅约7%,以立体桁架为主要承重体系的空间结构的整体稳定性能对活载分布不敏感。
(3)超长混凝土结构的温度应力不能忽视,工程最大拉应力出现在降温工况下的首层室外平台与室内交界处,最大值为2.5 MPa,温度应力随楼层增加自下而上逐层减小。
(4)工程大跨度楼盖难以满足规范规定的频率要求,采用调频质量阻尼器是降低楼盖竖向加速度的有效方法,减振率>50%。

