基于Matlab的Gauss-Seidel迭代法电力系统潮流计算研究
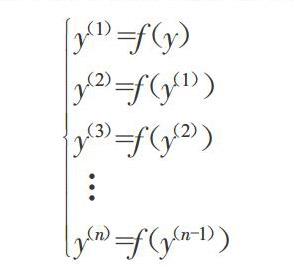
摘要:我国当前电力系统已经开始向大规模和高集成化方向发展,Matlab软件在研究过程中可以对电力系统发挥模拟作用,但是对于电力潮流来说,需要在获得数据以及具体节点之后,通过程序处理获得参数。在电力系统潮流计算阶段需要选用最科学的算法,由于Gauss-Seidel迭代法可以降低计算误差,所以在提高计算精度方面发挥着重要作用。基于此,介绍了Gauss-Seidel迭代算法基本原理以及Gauss-Seidel迭代算法用于潮流计算的基本原理,进一步分析了基于Matlab的Gauss-Seidel迭代算法电力系统潮流计算方法。
关键词:Matlab软件;Gauss-Seidel迭代法;电力系统潮流计算
0 引言
在迭代法的使用过程中,无论何种处理方法都会形成一定误差,经过多次迭代后,当采用同一数值参与计算时,则该误差会持续增加,甚至在一定情况下产生的误差会高于原始数值。对于本文选用的Gauss-Seidel迭代法,其优势是能够在形成迭代结果后,通过对该结果与下一步处理结果进行横向对比并直接利用,从而形成精准的计算结果。
1 Gauss-Seidel迭代算法基本原理
1.1 算法使用流程
该算法的使用流程是根据数学原理得到某一参数,计算方法可以表现为y=f(x),则迭代过程可以表示为:
y(1)=f(y)y(2)=f(y(1))y(3)=f(y(2))y(n)=f(y(n-1))
将不同流程得到的外值代入到同一个计算方程,以获得第二步结果,经过多次运算之后,每一步得到的结果都会产生一定差异。为了确定最终取得的运算参数,需要设定对比参数,计算方式为:
|y(n)-y(n-1)|≤ε
其中方程右侧为计算对象在多次计算中允许的最大误差值,需要注意的是,对于选用的算法中,函数加工厂“f(x)”中可以有多个自变量,但是因变量只能有一个,即:
y=f(x1,x2,x3,…,xn)
要根据实际的计算对象,合理确定自变量的数量和数值。
1.2 相关参数的处理
在参数处理过程中,一个参数为自变量,另一个参数为因变量,无论是何种算法都会设定一个标准值,而该标准值通常用于说明计算过程中产生的各阶段的误差程度[1]。通常情况下,该结果需要按照行业以及学科知识的要求设置,而具体计算工作由专业算法和软件自主完成,并且只有在确定多次计算结果之后,才可以得到最精确的指标。
1.3 最终结果的获取
事实上,在每一次迭代过程中都会产生一定的固定结果,但是不同的计算阶段数据生成的实际误差存在差异,只有在误差能够保持学科要求时,获得的结果才可实际使用。另外在每一步的计算阶段,都需要将产生的误差值加入到持续性的迭代算法内,而该迭代算法在融合了误差值后具有更高的精度,利用该方法可以使实际获得的结果具有可靠性。
2 Gauss-Seidel迭代算法用于潮流计算的基本原理
2.1 计算参数的确定
计算参数的确定要根据电力系统的自身运行标准和研究对象确定,比如对于电力潮流来说,由于主要的评价标准是某节点中的功率和其余节点间的功率比值,尤其是对于线路的上游和下游区域,当下游的实际功率高于上游时,则会出现逆潮流现象,对电力系统造成破坏,所以无论是实际检测,还是模拟运算,首先确定的参数是当前电力系统中的各个节点,其次通过对电压电流的分析,确定这两个节点的功率数值,并将获得的参数纳入计算方程中,可以在多次迭代之后和设定的标准值对比,当发现某参数经过多次迭代之后和标准值之间的误差小于设定标准,可确定当前整个潮流系统处于稳定运行状态。最后是实际分析,制定线路系统的优化方案。
2.2 计算公式的确定
在计算公式的建设阶段,要确定潮流的变化方法和计算流程,并且将各时间点和工作步骤中产生的实际参数纳入后续的计算范畴。通常情况下,由于迭代算法中计算公式不出现变化,所以可按照该方式研究最终的计算成果,让获得的结果可以更好地描述实际情况[2]。考虑到功率的计算方式为电压和电流的乘积,且对电流的计算和检测难度较小,所以主要分析当前不同节点的电流数值,此外根据不同节点的有功和无功功率数值,可获得第2个节点的电压以及第n个节点的电压数值,将其纳入实际的潮流计算公式内并可以得到实际的计算结果,以对平衡节点的电力参数进行讨论。由于已经在计算中获得了电压值,将该参数直接代入潮流迭代公式中进行多次迭代计算即可。由于向某节点注入的有功功率和电压大小已经给定,所以可以将其使用到迭代计算公式内,并对该节点的无功功率预先计算,根据功率和电流的表达式,并且加入需要考虑的电压值参数,则可使获得的结果得以精确计算。
2.3 计算节点的确定
在计算节点的确定过程中,由于不同的计算方法具有一定的误差,比如某节点为发电机节点而另一节点为输电端节点,这两个节点的计算公式必然不同。基于Matlab的数据分析过程要求,要根据已经建成的电力系统模型确定不同的节点方式,同时将获得的电压参数和电流参数代入迭代算法,获得的不同电压值和电流值都可以纳入该算法体系,以得到最终结果,并通过比较确定潮流情况。
3 基于Matlab的Gauss-Seidel迭代算法电力系统潮流计算方法
3.1 编程原理的确定
编程原理的确定阶段要根据Matlab的专用编程语言,在实际研究过程确定某节点类型,分为发电机节点、配电侧节点等,由于计算参数和计算方式已知,所以在编程阶段可以将工作数值纳入实际的编程体系中,并且按照时间变化设定相关参数。另外对于共轭电压值,只需要做出相关处理即可,采用迭代算法可以得到節点电压和运行相位角,在计算过程需要建立不同节点的导纳矩阵,对其初始化后设定初始运行状态值,并分析在经过一段时间以及多步骤分析后可以取得的作用效果,把获得的电压值输入原有的迭代算法,同时分析在不同时间节点中该节点的实际运行参数。
3.2 软件编程阶段
软件编程阶段要容纳电力学的各类参数、电力系统各节点的运行位置、不同节点电力学参数的变化方程等,通过所有数据的分析才可以将其加入实际的潮流计算阶段。此外在后续的运行过程需要对相关方程和编程结果进行预处理,该过程中一方面会设定初始运行值,另一方面要研究该数值的后续运行情况,以形成实际的运行指标,当确定该指标符合对比值要求时,则可确定目前的节点潮流可以符合系统的正常运行指标。
3.3 数据导入工作
在数据导入阶段,首先要设置整个供配电网络的初始运行值,包括电压参数、电流参数以及节点参数,并设定不同节点的电压变化情况,按照实际运行阶段的电力参数运行模式设定[2]。其次是设定专用的描述方程,包括电压的变化方程、电流的变化方程以及实际的对比方程等,并且将实际的迭代算法与电力学的相关变化方程進行对比,当发现实际的作用阶段,数据在经过了长时间运行之后,可以取得在不同运行时间点上的节点功率参数,经过横向对比,可研究当前该参数的差值是否超出了限定标准,若发现存在这一问题时,可确定当前的作用形势下该电力系统无法保持稳定运行状态。最后是对电力系统的优化,以解决目前存在的潮流问题。
3.4 计算结果的获取
在计算结果的取得和研究阶段,要研究的参数包括电力输出节点的电压初始值、发电机节点的相位角初始值以及经过一段运行时间之后的电力参数,并让该参数参与对比,尤其是对于发电机节点和功率输出节点,要分析不同发电机节点的运行参数。通过该形式一方面可以研究当前发电机的发电功率是否可以符合用电指标,另一方面可研究不同的发电机节点运行过程是否会出现逆潮流问题。比如,发现上游的发电机节点功率参数为U1,下游的发电机节点功率参数是U2,其中前个数值小于后个数值,则可确定该供电系统会出现逆潮流问题。
4 结语
综上所述,基于Matlab的迭代算法使用阶段,由于迭代算法可以对不同运行过程的操作进行全方位考虑,所以在实际运行过程中,可通过当前电力系统的相关参数确定运行状态,找到实际的运行指标。Matlab软件经过编程之后,可以在数据优化和基础数据获取阶段,经过多次计算得到成果,以便研究该电力系统是否存在故障以及逆潮流问题。
[参考文献]
[1] 韦雅,文耀宽,田珂,等.基于时间序列线性大数据分析的电力系统潮流计算方法[J].机械与电子,2020,38(1):32-35.
[2] 安军,宋俊达,葛维春.大规模电力系统潮流计算收敛性诊断与调整方法[J].电力自动化设备,2020(2):1-6.
收稿日期:2020-01-16
作者简介:宋阳(1979—),男,四川乐山人,硕士研究生,高级工程师,研究方向:电力系统分析、电网稳定分析与潮流计算等。

