动态加载方式下防爆墙动力响应分析
赵旭 侯博晗 席聪 谭英华
摘要:为分析防爆墙在不同爆炸载荷下的动力响应和破坏机理,研究波纹板式防爆墙与平板式防爆墙的差异,分别采用三角波加载和基于流固耦合方法的爆炸仿真2种动态加载方式模拟爆炸载荷。分析结果表明:三角波载荷可以较好地模拟爆炸载荷且具有明显的计算速度优势。分析得到2种类型防爆墙的P-I曲线,通过对比发现波纹板式防爆墙的抗爆性能优于平板式防爆墙。
关键词:防爆墙;爆炸载荷;三角波;流固耦合;动力响应;P-I曲线
中图分类号:TP391.99;TU352.13文献标志码:B
0 引言
抗爆设计对可能发生爆炸灾难风险的建筑具有重要意义。与其他防爆措施相比,防爆墙具有经济、空间布置灵活、防爆能力强等优点。国内关于防爆墙的研究起步相对较晚,但是近年来涌现大量关于墙体抗爆性能的研究成果。王仲琦等基于多物质流体的欧拉算法,对爆轰产物采用JWL状态方程,并运用其自行编制的SMMIC通用程序,研究爆炸冲击下不同防护墙对冲击波发展过程和扩散规律的影响。吴媛媛等利用LS-DYNA软件,对近地爆炸下刚性墙绕流现象进行数值模拟,研究超压时程规律及其影响因素。师吉浩等运用LS-DYNA软件分析3种波纹板式防爆墙在不同爆炸载荷作用下的动态响应和破坏机理,拟合3种类型波纹板式防爆墻的抗爆评估P-I曲线,为初始抗爆设计提供参考。张雄等研究物质点法模拟爆炸问题,在物质点有限元法和局部多重背景网格算法基础上开发针对冲击爆炸问题的三维显式并行MPM数值仿真软件MPM3D,为爆炸研究提供工具。
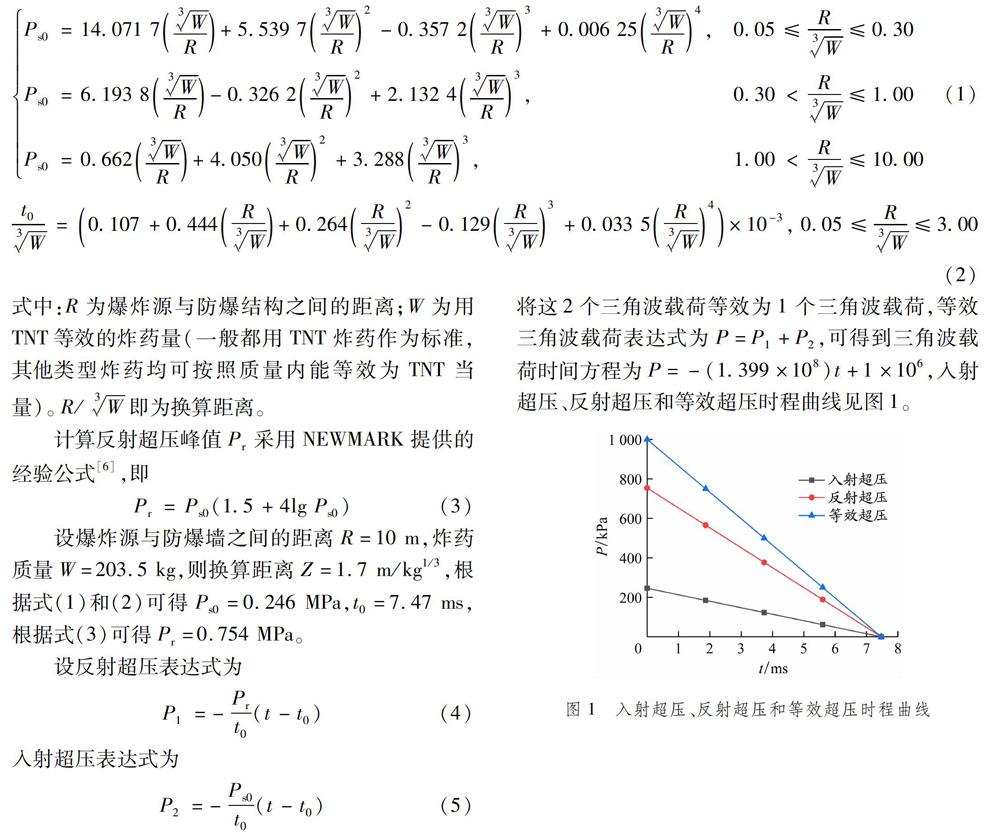
三角波加载和通过建立欧拉区域模型进行流固耦合爆炸模拟分析是研究防爆墙动力性能常用的2种动态加载方式。后者往往计算成本较高,且参数不易修改。本文分析比较2种不同爆炸载荷动态加载方式下防爆墙的中心位移响应,结果表明2种动态加载方式下模拟分析结果吻合较好,验证三角波动态加载方式的合理性和有效性。三角波加载具有明显的计算速度优势,因此本文采用三角波加载方式对比分析波纹板式防爆墙和平板式防爆墙的防爆性能,并借助P-I曲线直观研究2种防爆墙性能的差异。
1 2种动态加载方式
1.1三角波加载爆炸模拟
依据防爆墙与爆炸源的距离不同,爆炸可分为远距离爆炸和近距离爆炸。研究爆炸冲击载荷时,需要将所有的爆炸物换算为TNT炸药,距离也要用换算距离替代。由于爆炸过程环境变化的复杂性,冲击波各参数很难通过理论分析获得。本文选择HENRYCHL提出的无限域空气中炸药爆炸峰值压力经验计算公式(式(1)和(2))确定爆炸冲击波的人射超压峰值平S0及其对应时间t0。
1.2 基于流固耦合方法的爆炸模拟
任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)算法是NOH在研究有限差分法时提出的,后来被HUERTA等引人有限元法中,其基本思想是计算网络既不固定也不依附于流体质点,而是可以相对于坐标系任意运动。
这种方法最先出现在数值模拟流体动力学问题的有限差分法中,其拥有拉格朗日和欧拉2种算法的优点:首先,在结构边界运动问题的处理上继承拉格朗日算法的优势,能够有效追踪物质结构边界的运动;其次,在内部网格划分上吸收欧拉算法的优势,使其内部网格单元独立于物质实体而存在。但是,与欧拉算法网格不完全相同,ALE算法网格可以根据定义的参数在求解过程中适当调整位置,使得网格不会出现严重畸变,这种方法在进行爆炸模拟分析时非常有利。
基于JWL状态方程理论,采用通用有限元软件LS-DYNA中的。Me_Multi_Material_Group多物质单元实现使用流固耦合算法模拟爆炸的过程:对炸药和空气材料采用欧拉算法,其他结构采用格朗日算法,然后通过流固耦合的方式模拟两者之间的相互作用。
2 计算模型
2.1 平板式防爆墙几何模型
采用方形平钢板作为防爆墙,钢板尺寸为8.80m×8.80m,厚度为0.02m,分别采用2种动态加载方式模拟其承受的爆炸载荷。钢板单元类型选择SHELLl63,炸药单元和空气单元都用三维显式结构实体单元SOLIDl64。炸药尺寸为0.50m×0.50m×0.50m的立方体,空气为9.00m×9.00m×13.50m的立方体,防爆墙与爆炸源的距离为10.00m,防爆墙四周为固支约束。防爆墙流固耦合计算模型见图2。
2.2 平板式防爆墙材料的本构模型
在计算模型中,钢采用LS-DYNA中的*Mat_Plastic_Kinematic材料模型模拟,该材料模型可描述各种各向同性硬化和随动硬化塑性模型,同时还可以考虑应变率和时效的影响。通过在0(仅随动硬化)和l(仅各向同性硬化)之间调整硬化参数卢实现随动或各向同性硬化。钢板采用考虑应变率效应的Cowper-Symonds本构模型,本构方程为
2.3 炸药和空气材料参数及其状态方程
在数值模拟中,目前广泛使用的爆轰产物状态方程主要有BKW、LJD、JCZ和JWL等,此处TNT炸药的材料模型采用JWL状态方程描述,即式中:P为爆轰产物压力;V为相对体积;E为TNT炸药单位质量的内能;A、B、R1和R2为材料常数。TNT炸药JWL状态方程相关参数见表2,其中v为TNT炸药的爆速。
采用理想气体状态方程描述空气,其压力P和内能e0的关系为
P=(r-1)ρ0e0(8)
式中:ρ0为空气密度;e0为单位质量气体的内能;r为材料常数。空气相关参数见表3。
2.4 单元收敛性检验
先选取40000个单元,然后以40000个单元为公差等差式增加单元数量,共采用6组单元进行模型网格依赖性分析。防爆墙中心最大位移随单元数量的变化规律见图3。
由图3可知,当单元数量超过120000个之后,单元数量对计算结果影响很小。因此,确定计算網格单元尺寸为0.20m×0.20m×0.20m,防爆墙单元总数为7744个,空气和炸药的单元总数为150212个,模型总计157956个单元。
3 计算结果分析
3.1 爆炸冲击波分布变化规律
采用欧拉单元建立炸药和空气模型,采用拉格朗日单元建立防爆墙模型,进行流固耦合计算,得到不同时刻空气和防爆墙的压力云图,分别见图4和5。由此可观察爆炸冲击波在空气中的传播:在9ms时冲击波完全到达防爆墙,此时冲击波波面近似为平面,且除防爆墙中心部分外其他各处压力基本相等。
3.2 2种动态加载方式下防爆墙的动力响应对比
在冲击载荷下,防爆墙最大位移发生在钢板中心位置,因此以中心点的最大位移为研究对象,其时程曲线见图6。
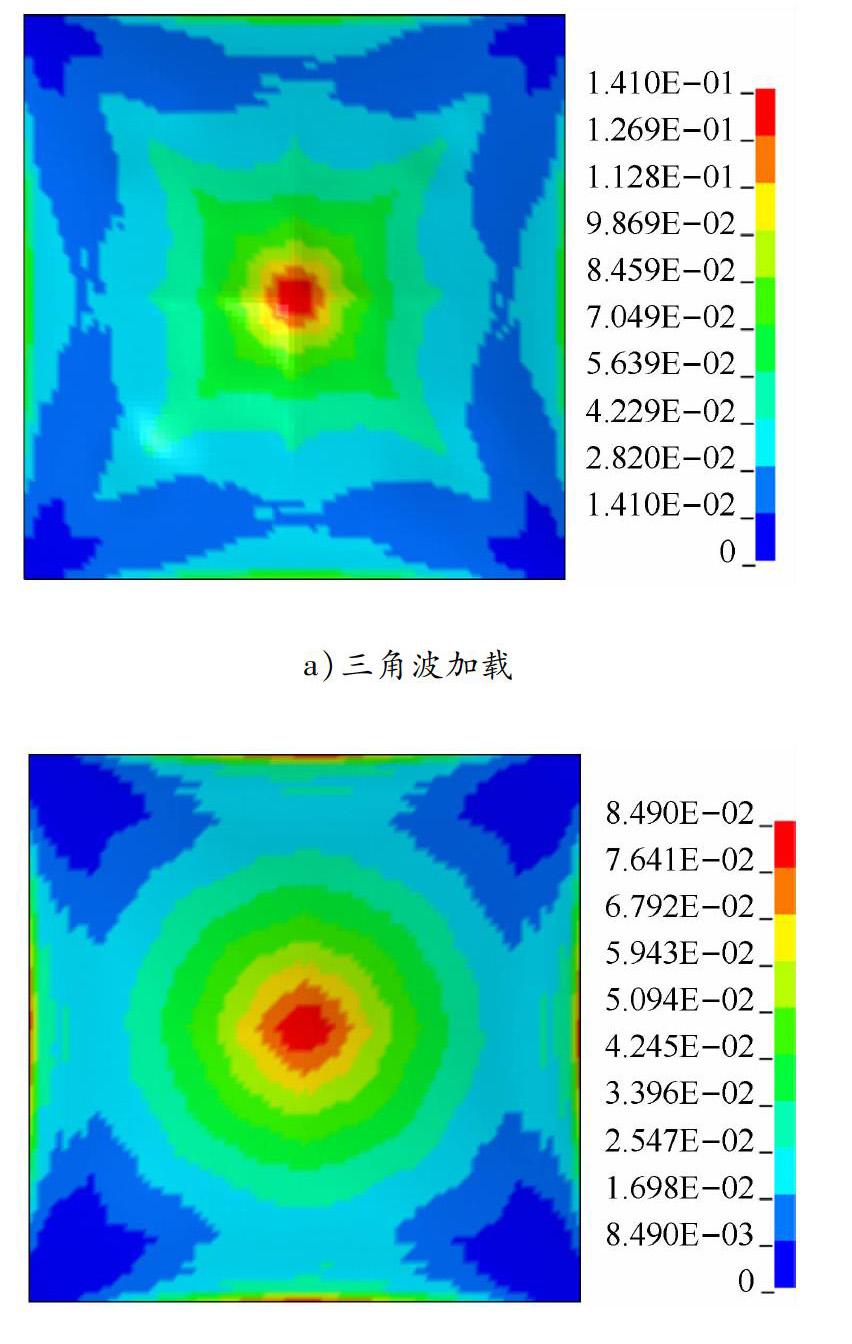
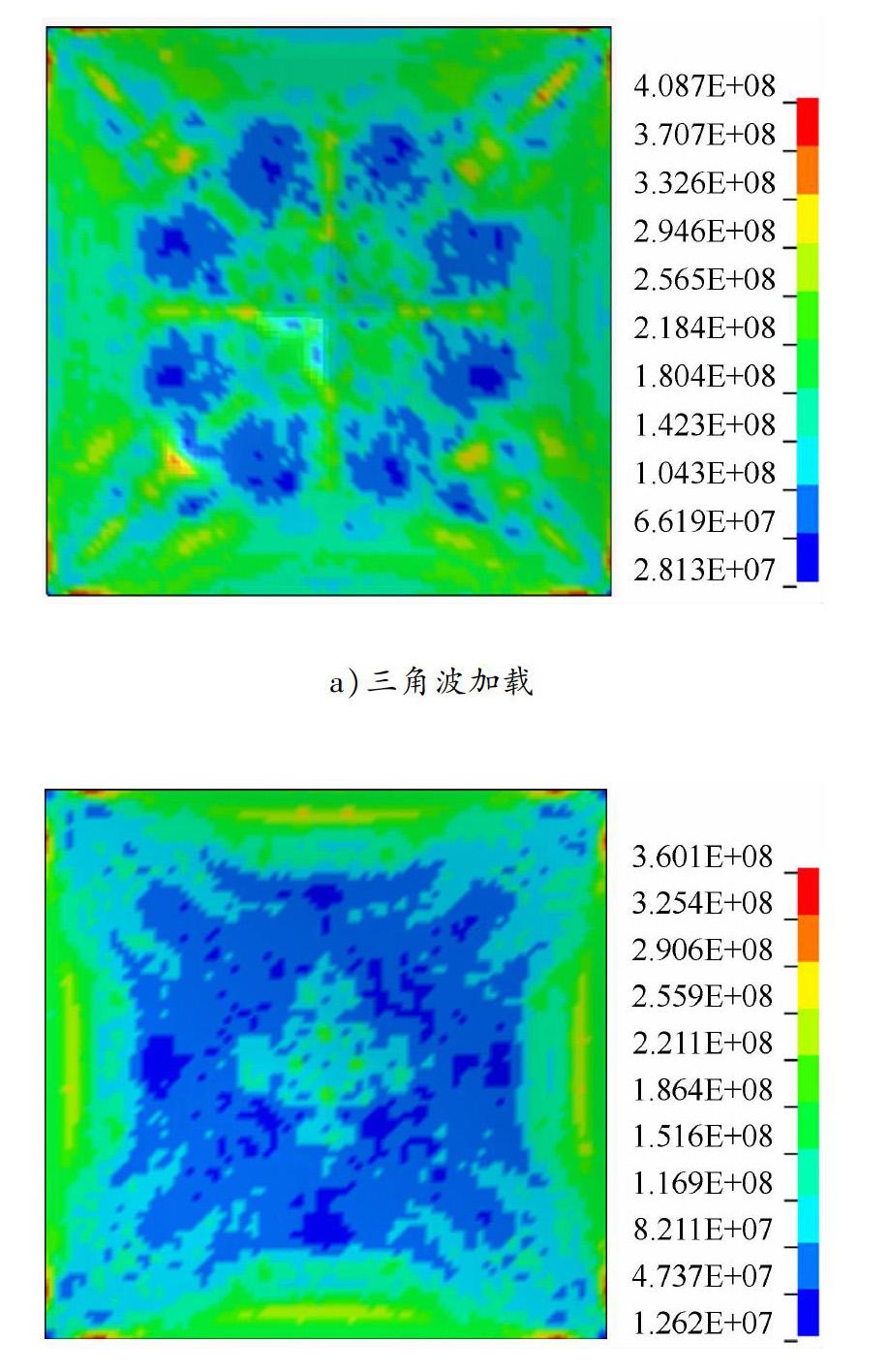
由图6可以看出,在三角波动态加载方式下,防爆墙的最大塑性位移较大,与流固耦合计算载荷位移的差值约为流固耦合计算载荷位移结果的22%。2种动态加载方式下防爆墙等效应变云图和VONMises应力云图分别见图7和8。由此可以看出:在2种动态加载方式下,防爆墙等效应力和等效应变云图均大致相同,其应力、应变分布规律基本一致;三角波载荷下的最大等效塑性应变较大,两者之间的差值为流固耦合计算载荷下应变结果的60%;三角波载荷下最大VON Mises应力较大,两者之间的差值为流固耦合计算载荷下应力结果的13%。
综上所述,三角波载荷可以较好地模拟爆炸冲击载荷,且具有明显的计算速度优势,因此研究简单计算模型采用三角波载荷可节约计算成本。
4 三角波动态加载方式下波纹板式防爆墙与平板式防爆墙动力响应对比
4.1波纹板式防爆墙模型
取波纹板式防爆墙与平板式防爆墙尺寸相同,均为8.80m×8.80m,其材料模型也与平板式防爆墙相同,波纹板式防爆墙有限元模型见图9。波纹板式防爆墙四周仍采用固支约束,网格尺寸为0.10m×0.10m。为比较2种防爆墙的抗爆性能,设2种防爆墙用钢量相同,因此波纹板式防爆墙厚度取6.0mm,平板式防爆墙厚度为7.4mm,借助P-I曲线对比分析两者的防爆性能。
4.2 P-I曲线
依据文献[11]绘制P-I曲线,采用三角波加载模拟爆炸载荷。绘制P-I曲线首先需要确定失效准则。下面是2种常用的失效准则。
4.2.1 以失效应变定义失效准则
平板式和波纹板式防爆墙等效应变云图分别见图10和11。计算分析结果表明:平板式防爆墙的中心位置率先达到失效应变;波纹板式防爆墙四周的约束边界处率先达到失效应变。
以失效应变定义P-I曲线的失效准则时,波纹板式防爆墙的P-I曲线形状不理想,其原因是难以得到波纹板式防爆墙约束边界处单元的真实应变,这是约束引起的应力奇异现象导致的。若以达到失效应变作为失效准则,而波纹板最大应变出现在被约束波纹板的边界处,则无法获得有效应变值,说明该失效准则不适用于本文方法。
4.2.2 以最大塑性位移定义失效准则
一般将防爆墙的极限状态作为防爆墙抗爆设计的依据,因为爆炸事故是低概率事件,所以建筑结构的抗爆设计通常不够充分,其应变、应力和挠曲位移极易超越弹性极限,因此应以极限状态考虑爆炸事故设计状况。在爆炸载荷作用下,防爆墙的典型屈服极限值为墙长l的1/40-1/25,这里选取1/25,将最大塑性位移达到1/25=352mm定义为波纹板式防爆墙的失效准则。
波纹板式防爆墙与平板式防爆墙的最大塑性位移均出现在防爆墙中心位置。采用最大塑性位移失效准则绘制2种防爆墙的P-I曲线,见图12。
由图12可知,平板式防爆墙冲量的渐近线在波纹板式防爆墙冲量渐近线的左侧,两者的准静态渐近线基本一致;与平板式防爆墙相比,波纹板式防爆墙的动态加载区段和冲量加载区段所对应的安全区域均较大,准静态加载区段对应的安全区域基本相同。综合分析,波纹板式防爆墙的抗爆性能优于平板式防爆墙。同时,波纹板式防爆墙边缘和中间部分的应变一直较大,若将这2处区域予以加强,可更好地增强波纹板式防爆墙的抗爆性能。
5 结论
采用通用有限元软件LS-DYNA对2种动态加载方式下防爆墙的动力响应进行分析,结论如下。
(1)三角波动态加载方式的计算结果与基于流固耦合方法加载的仿真分析结果吻合较好,采用三角波动态加载方式模拟爆炸冲击载荷具有明显的计算速度优势,因此研究简单计算模型时采用三角波载荷可节约计算成本。
(2)当以最大塑性位移作为失效准则时,与平板式防爆墙相比,波纹板式防爆墙动态加载区段和冲量加载区段所对应的安全区域均较大,准静态加载区段对应的安全区域基本相同。综合分析,波纹板式防爆墙的抗爆性能优于平板式防爆墙。
(3)对于波纹板式防爆墙,宜对其边缘和中间部分进行加厚处理,进而优化波纹板式防爆墙的抗爆性能。

