基于塑性修正系数的矩形薄板屈曲计算方法
童杰 李娟 张冰珂 苏江 侯鹏飞

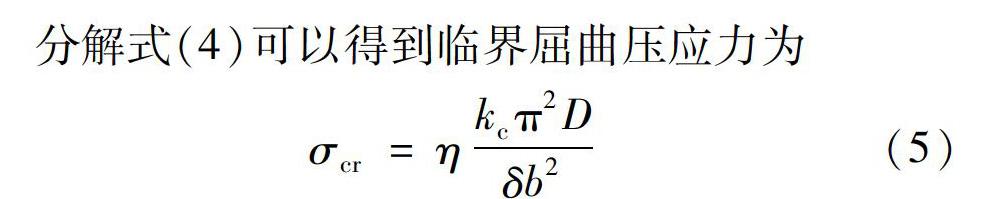
摘要:为探究薄板的屈曲破坏性能,以飞机机身设计中最常用的铝合金薄板结构为研究对象,利用金属材料塑性修正系数分析矩形薄板的屈曲失效,得到在均布压力和不同约束条件下矩形薄板的临界屈曲应力。数值仿真算例及其有限元计算结果对比,验证该方法的正确性。
关键词:塑性修正;薄板;屈曲应力;失效
中图分类号:V214.35;TB115.1文献标志码:B
0引言
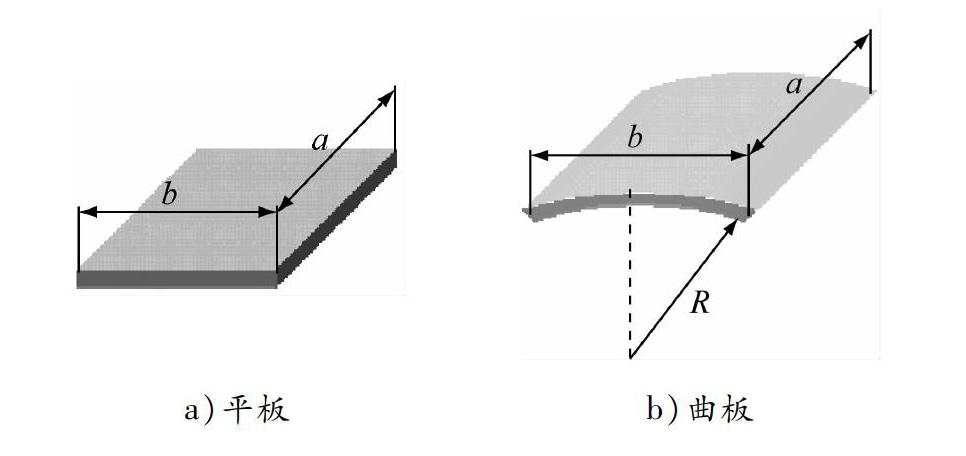
在现代飞机和汽车结构中,很多部件设计为板杆结构,因此大量使用平板和曲板,如飞机地板、框梁肋的腹板等多为平板结构,飞机机身蒙皮、汽车车身等多为曲板结构。在飞机总体有限元模型中,一般将薄板结构简化为剪切板或薄板,只承受拉压和剪切载荷,不承受弯曲载荷。这些结构在建立计算模型时一般简化为薄板单元,在结构破坏设计计算中主要考虑屈曲失效。
平板和曲板结构示意见图1。当板的厚度δ与板的宽度b的比值δ/b在1/80-1/5范围内时,这样的板就称为薄板。薄板结构广泛应用于航空航天、土木、海洋和机械工程等众多领域。若薄板在纵向载荷作用下处于弯曲平衡状态,则此时的纵向弯曲或压曲称为屈曲。
陈贞钜计算在中面载荷下正交各向异性带孔薄板各单元的受力分布,并用高精度板弯曲单元计算其临界屈曲载荷和有中面力时的横向振动特征,总结开孔大小、材料性质、弹性主方向、约束条件和中面载荷类型对屈曲临界载荷和横向振动特征值的影响规律。沙云东等研究在热、声载荷作用下各向同性矩形薄壁结构的大挠度非线性控制方程,推导四边简支板的模态频率及其在温度梯度作用下的热屈曲温度差,并通过有限元数值计算,得到在热、声载荷作用下简支板热屈曲前后的动态应力响应。马连生等基于经典板理论研究在边界面内均布压力作用下,功能梯度材料圆形板的轴对称屈曲方程,得到功能梯度材料圆(环)板的临界屈曲载荷,并分析材料的梯度性质、内外半径比和边界条件对板临界载荷的影响。钱伟长等用合成展开摄动法,把外场解和内层解结合起来,求解圆形薄板大挠度问题。ULLAH等采用广义积分变换方法得到矩形薄板的精确解析屈曲解,根据板的边界条件,采用振动梁函数作为积分核构造积分变换,将积分变换应用于板的高阶偏微分方程的基本控制,利用梁函数的一些固有性质,将问题转化为线性代数方程组,由该方程组快速地得到精确的解析解。该分析方法的主要优点是简单、通用,不需要任何预先确定的变形函数。LI等用一种特殊的辛叠加方法讨论双轴向压缩下完全自由板的典型屈曲问题,提出辛空间哈密顿系统的解,给出新的屈曲载荷综合分析结果。该方法收敛速度快、精度高,适用于多层板问题的解析建模。WANG等研究基于辛叠加法的矩形薄板屈曲解析解,提出一种基于哈密顿系统的变分理论,利用拉格朗日乘子法求解辛空间薄板屈曲問题,但是文献中没有提及利用材料塑性修正系数对薄板屈曲问题进行研究。
基于以上研究成果,本文在金属材料的Ramberg-Osgood特性曲线的基础上,对屈曲计算结果进行塑性修改,研究在均布载荷作用下的四边简支矩形薄板屈曲计算方法。首先,基于薄板压曲微分方程,求解临界屈曲压应力;其次,根据边界约束条件和薄板尺寸结构选择不同的计算参数,对临界屈曲压应力进行迭代修正计算,得到准确的临界屈曲压应力;最后,通过数值算例与Nastran求解器计算结果的对比,验证此计算方法的正确性。
1 薄板结构的基本参数和基本方程
在现代飞机和汽车结构设计中,主要结构件多为金属结构,并以铝合金为主。必须要明确金属材料的弹、塑性关系,才能进行塑性修正计算。铝合金材料的弹、塑性关系可根据Ramberg-Osgood材料特性曲线(见图2)给出。式中:D为弯曲刚度;Fx、Fxy、Fy为中面内力。
2 平板屈曲分析
式中:η为塑性修正系数;kc为屈曲因数,其值取决于边界条件;δ为板厚。屈曲因数kc.的取值一般为:三边剪支一边自由时,kc=0.43;四边简支,a>b时kc=4,ac=(a/b)2+(b/a)2+2。
通常认为,当线弹性临界屈曲应力大于0.5δb时需要进行塑性修正计算,压缩载荷时塑性修正系数η的确定公式见表1。
3 数值算例
以平板在均布压缩载荷作用下的临界压缩屈曲应力计算为例,采用有限元法进行计算,与前文计算结果进行对比。
在计算模型中,薄板长边a=540mm,短边b=180mm,厚度δ=2mm。材料选择2024铝合金,其弹性模量E=70300MPa,泊松比ve=0.44,压缩屈服应力δcy=270MPa,Ramberg-Osgood系数nc=13。边界条件为四边简支,短边施加30MPa纯压载荷。薄板计算模型和参数示意见图3。
由此,可以得到δcr=32.04MPa。
在Nastran中进行有限元计算,边界条件为四边简支,计算单元为四边形单元,单元尺寸为2×2,共计划分24300个单元,计算结果应力云图见图4。
改变计算模型尺寸,应力计算结果见表2;改变边界条件,应力计算结果见表3。分析表2和3数据可知,与有限元计算结果相比,修正后的计算结果误差都小于2%。对比分析不同薄板尺寸下的屈曲应力可知,长度尺寸a和宽度尺寸b越接近,薄板的屈曲应力越大;在同等尺寸下,四边简支边界条件下的屈曲应力明显大于三边简支一边自由边界条件的屈曲应力。
4 结束语
利用金属材料的Ramberg-Osgood弹塑性特征曲线,对薄板受压临界屈曲应力进行塑性修正。在薄板压曲微分方程的基础上,给出临界屈曲压应力计算公式,分析多种边界条件下的修正系数;通过计算模型算例与有限元计算结果对比,验证本文计算方法的正确性,为工程设计中薄板屈曲计算提供参考。

