一类随机偏微分方程有限维约化的逼近

杨 敏，陈光淦*，李 琴

（1.四川师范大学数学科学学院，四川成都610066； 2.四川师范大学可视化计算与虚拟现实四川省重点实验室，四川成都610066）

随机不变流形为随机偏微分方程驱动的动力系统提供了一个几何结构刻画.Duan等[1-2]证明了一类随机偏微分方程的随机不变流形的存在性与光滑性.无穷维状态空间使得方程解的研究工作非常复杂.Wang 等[3]和 Roberts[4]证明了不变流形若是几乎处处渐近完备的，则可将无穷维系统约化到有限维.

Acquistapace等[5]证明了处处连续处处不可微的W（t）可由处处连续且可微的Φε（t）逼近，其中Φε（t）的定义见第2 节.Jiang 等[6]证明了带光滑噪声的随机系统的稳定流形可近似带不光滑噪声的随机系统的稳定流形.Wang等[7]应用Wong-Zakai逼近理论证明原系统可由简化的随机系统去逼近.

考虑一类带乘性高斯白噪声驱动的随机发展方程

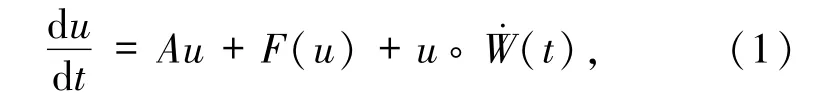
其中A、W、F 将在第 2节给出，“◦”是 Stratonovich意义下的乘积，且系统（1）通常乘积意义下的形式为

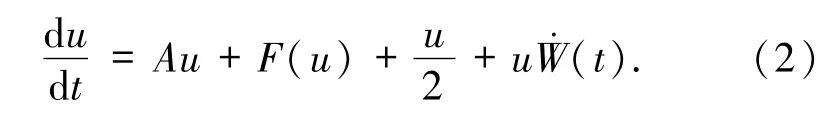
本文研究由处处连续处处可微的Φε（t）驱动的随机发展方程

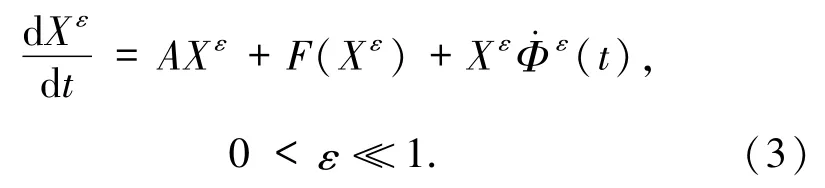
证明了系统（3）的有限维约化收敛到系统（1）的有限维约化.

1 预备知识

令空间H是一个实值可分的Hilbert空间，其范数为｜·｜，内积为〈·〉，线性算子A是H上C0半群｛etA｝的生成元.W（t）是标准的实值布朗运动，F是H上的非线性函数满足 F（0）=0和Lipschitz条件

其中LF＞0是Lipschitz常数.

假定σ（A）为算子A的谱，令

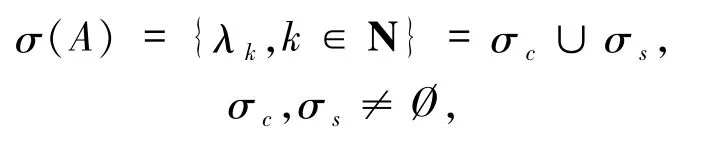
其中σc是一个有限的集合，且

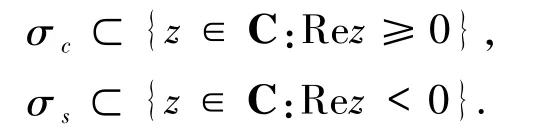
在空间H上做一个A不变分解，使得分别限制在 Hc和 Hs空间上的算子 Ac=A｜Hc和 As=A｜Hs，且满足

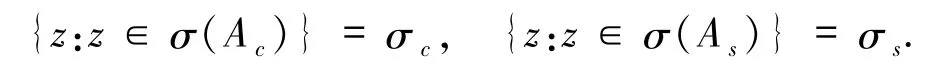
这里 H=Hc⊕Hs，Hc是一个有限维空间，且｛etAc｝是Hc上的解半群.假定存在常数α、β满足0≤α＜β，使得

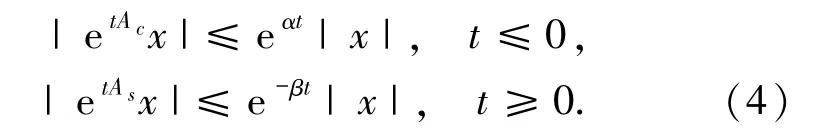
给定完备概率空间（Ω，F，P），在Ω上定义映射流 θ=｛θt｝t∈R：R ×Ω→Ω.如果映射｛θt｝t∈R满足条件：

（i）θ0=id，

（ii）对任意的 s，t∈R，有 θtθs=θt+s，

则称（Ω，F，P，θ）为测度动力系统[1].

如果映射

是（B（R）×F×B（H），F）-可测，且满足

（i）φ（0，ω，x）=x，

（ii）φ（t+s，ω）=φ（t，θsω，φ（s，ω）），s，t∈R，ω∈Ω，x∈H，

则称测度动力系统θ和φ构成的二元组（θ，φ）为随机动力系统.

考虑Langevin方程

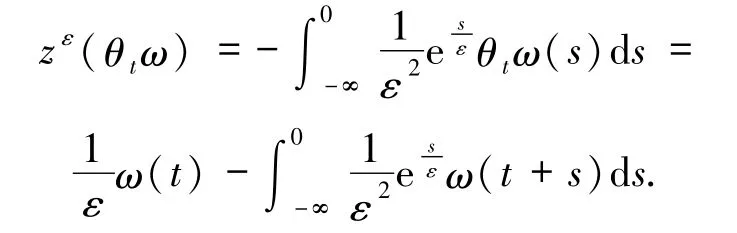
定义

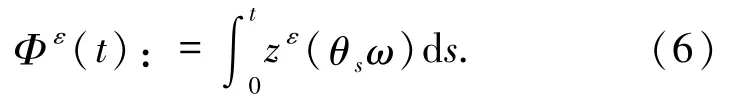
引理1.1[5]设 W（t）是 R 上的布朗运动.任给一个时间 T ＞0，则当 ε→0 时，Φε（t）→W（t）在[0，T]上是几乎处处一致的.

引进变换 T（ω，x）=xe-εzε（ω），系统（1）转化为

其中

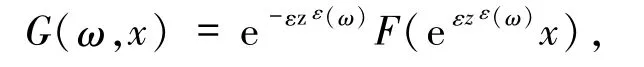
显然函数G和F有相同的Lipschitz常数LF.

引理1.2[1]假设 vε是系统（7）的解，那么

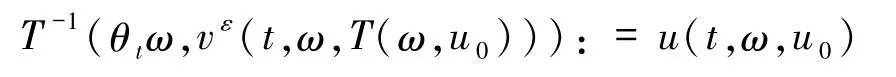
是系统（1）的解，其中T-1是T的逆变换，且

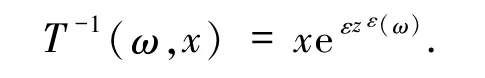
定义1.1假设M（ω）是随机动力系统φ（t，ω）的不变流形.如果对任意的 x∈H存在 y∈M（ω），使得

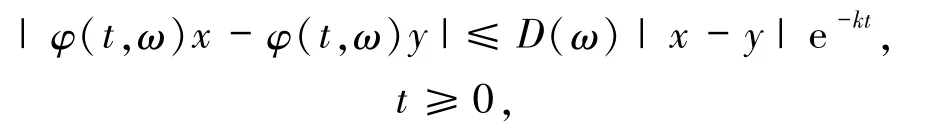
对几乎所有的ω∈Ω成立，那么称不变流形M（ω）是几乎处处渐近完备的，其中D（ω）是一个正的随机变量，k是一个正常数.

定义1.2给定一个正的随机变量δ，定义随机集合

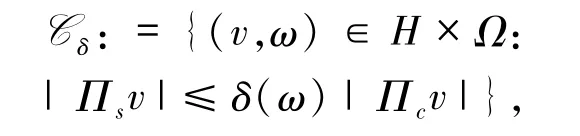
则 Cδ（ω）（ω）=｛v：（v，ω）∈Cδ｝被称作随机锥，这里投射算子 Πc：H→Hc，Πs=I- Πc：H→Hs，且 I是恒等算子.

定义1.3对于一个随机锥 Cδ（ω）（ω），如果存在一个随机变量≤δ，使得对几乎所有的ω∈Ω都满足

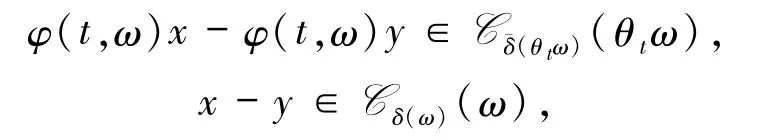
那么这个随机动力系统φ（t，ω）被称为有锥不变性，其中

下面给出本文一些所用符号说明.记φ（t，ω）、φε（t，ω）分别为系统（7）和（3）在空间（Ω，F，P，θ）上的随机动力系统，且

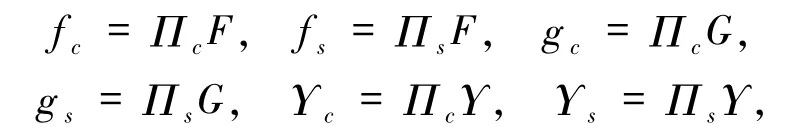
其中符号 Υ 代表｛u，vε，Xε，U，V，Y｝中任意元素.这里Πc、Πs如定义1.2中所给的投射算子.

2 有限维约化

假设 vε和 Xε分别为系统（7）和（3）的解，其初值分别为任给 η∈（-β，-α），定义2个Banach空间

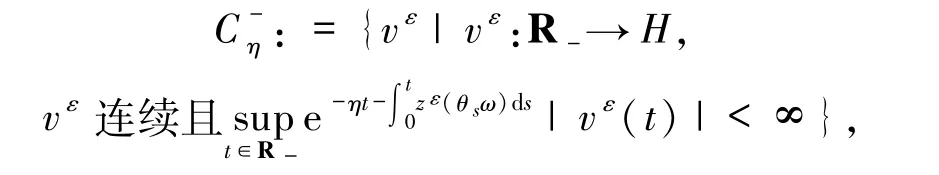
其范数为

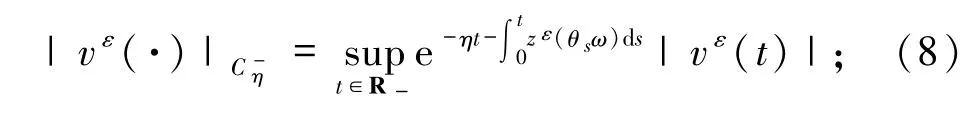
以及

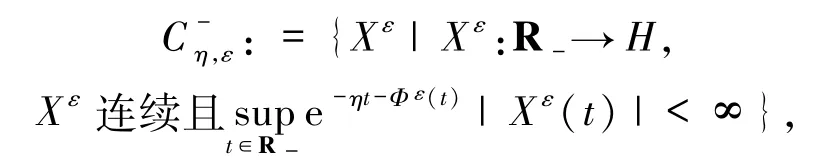
其范数为

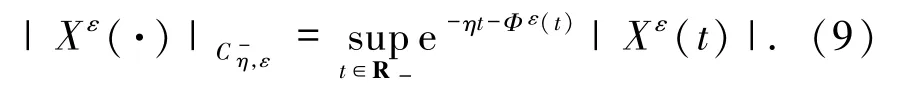
引理2.1[2，6]如果 LF满足条件

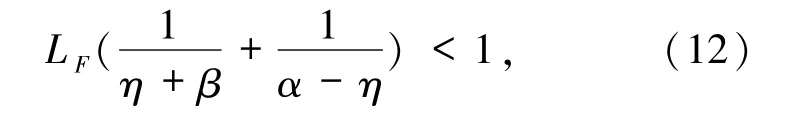
那么随机系统（7）和（3）分别有Lipschitz不变流形

进一步，取值于 Hs的 Lipschitz连续映射 hvε和 hXε满足

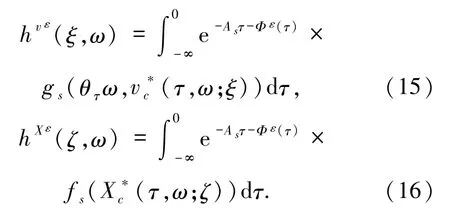
命题2.1[3]（i）如果（12）式成立，那么存在一个正的随机变量D（ω）和一个正常数k，使得对于随机系统（7）的任意解 vε（t，θ-tω），都存在一个轨道 V（t，θ-tω）∈Mvε（ω）满足

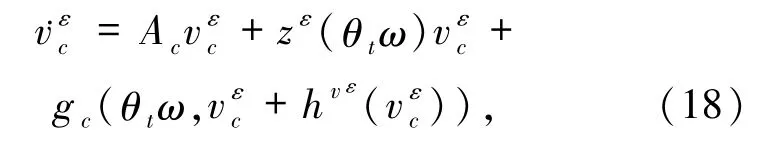
注2.1由引理1.2，系统（1）的轨道u=（uc，us）可约化到有限维空间Hc上且满足

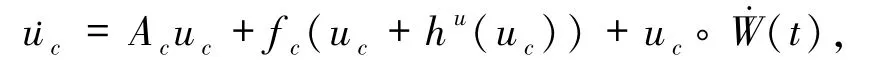
其中

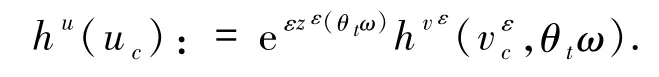
进一步，轨道 U=（uc，hu（uc））被称为系统（1）依赖于不变流形 Mu（ω）=｛ξ+hu（ξ）｜ξ∈Hc｝的解.

由文献[3]，如果给定最终时间 Tf＞0，则在t∈[0，Tf]时，系统（7）分别限制在空间 Hc和 Hs的解为

其中

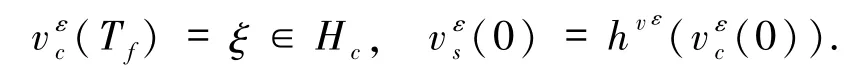
同理可得系统（3）分别限制在空间Hc和Hs的解为

其中

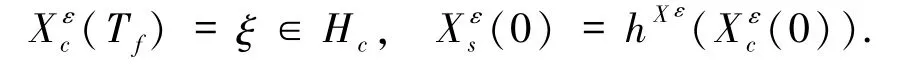
引理2.2[1]若（12）式成立，则对任意的 Tf＞0，（19）式有唯一解且（20）式有唯一解进一步，对任意 t≥0，有

引理2.3[1，3]（i）如果（12）式成立，那么系统（3）的随机动力系统 φε（t，ω）具有锥不变性.

（ii）如果存在 t0＞0，使得任意的 x，y∈H，φε（t0，ω）x- φε（t0，ω）y∉Cδ（θt0ω），那么

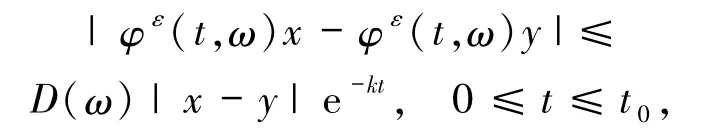
其中，D（ω）是缓增的随机变量，

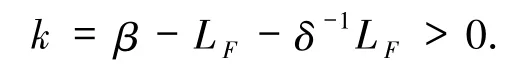
命题2.2（i）如果（12）式成立，那么存在一个正的随机变量D（ω）和一个正常数k，使得对于随机系统（3）的任意解 Xε（t，θ-tω）都存在一个轨道 Y（t，θ-tω）∈MXε（ω）满足

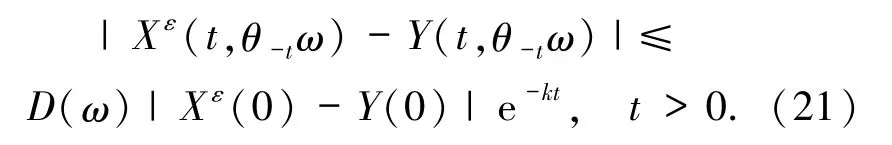
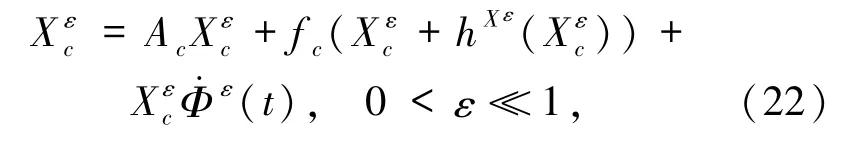
证明任给ω∈Ω，讨论系统（3）的解

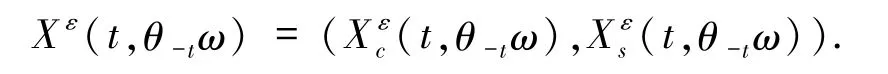
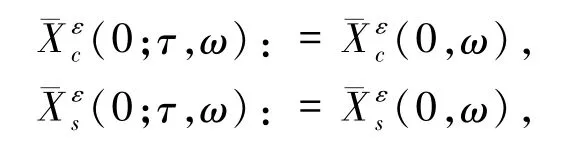
有

其中β+η＞0，且记

根据锥不变性有

因此，对几乎所有的ω∈Ω，S（ω）是Rn空间上的一个有界集.选一个序列τm→∞使得

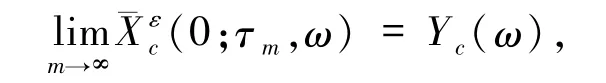
其中Y（ω）是可测的.令

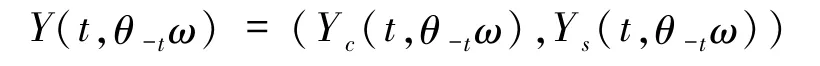
且满足初值

则 Y（t，θ-tω）∈MXε（ω），且

即 MXε（ω）几乎处处渐近完备，（21）式得证.

由（i）可知 Y（t，θ-tω）∈MXε（ω），且 MXε（ω）几乎处处渐近完备，由文献[3]的方法，则可约化到有限维空间 Hc上，且，命题2.2 得证.

3 有限维上的逼近

引理3.1假设是系统（7）和系统（1）的有限维约化，则对几乎所有ω∈Ω有

证明由引理1.2，有，且当 ε→0 时，则此时

引理3.1得证.

引理3.2假设是系统（7）和系统（3）的有限维约化，则对几乎所有ω∈Ω有

证明由（19）～ （20）式和 Φε（t）的定义，则对任意的 t∈[0，Tf]有

定理3.1假设是系统（3）和系统（1）的有限维约化，则对几乎所有ω∈Ω有

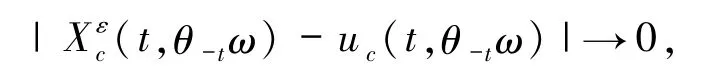
由引理3.1和3.2，定理3.1显然成立.

致谢四川师范大学2019年研究生优秀论文培育项目（201903-10）对本文给予了资助，谨致谢意.