大观念下指向学生核心素养的单元整体设计——“除数是两位数笔算除法”单元TUKE目标的制定

哈尔滨市清滨小学 刘清姝 刘 晶

学习目标是课堂学习全过程的灵魂。充分、客观的学情评估是清晰“灵魂”指引方向和目的的前提。在制定“除数是两位数笔算除法”单元TUKE目标时，我们对学生的先期学习经验进行了评估，以了解学生真正的学习起点，学习困难和发展需求，同时为形成学生思考的关键问题提供依据。

1.学生先期学习经验评估。

进行单元整体设计前，我们抽取了四年级一个班级42名学生进行了前测。

在口算“150÷30”这道题时，有36人口算正确，但他们的思考过程并不完全相同。主要有这样三种情况：一是采用画图方式，画了15个圆，把15个圆平均分成3份，每份是5个。进一步文字解释，有这样的10组，每组都是得5，所以150÷30=5。二是直接采用文字叙述，先不看150和30末位的“0”，15÷3=5，所以 150÷30=5。三是想 5个 30就是150，所以150÷30=5。从三种情况来看，除数是整十数的口算对学生来说并不困难，在正确的35人中，除2人用除法的意义画图解决，其余学生都自觉迁移了表内乘除法知识用口诀或想乘算除的方法口算。而对错误的6人访谈发现，他们也无一例外地想到了利用口诀计算15÷3=5，但看到被除数和除数末位都有一个“0”所以商的末位也要有一个“0”，出现了“150÷30=50”的错误。从学生的反馈我们看到，不管采用何种方法，口算结果正确与否，他们都能根据表内乘除法的学习经验解决新的问题，知识的同化现象在学生进行新的学习前已然发生。

计算“168÷6，168÷24”，能用竖式准确计算168÷6=28的有39人，其中34人对于商的位置及过程含义分析准确无误。这说明经过三年级上学期的学习后，学生对除数是一位数除法的笔算方法掌握扎实，对算理的理解也较为清晰。对比168÷6，计算“168÷24”时学生的解答和分析就呈现出较大的差异。主要有这样几种情况：（1）有9人用文字表达，还没学过除数是两位数的题，不会做。（2）有13人知道除数是两位数，就先看被除数的前两位，16÷24，不够除，要看前3位，但是不能直接看出168里面有几个24，不能确定商几。（3）有4人借“想乘算除”确定商的范围，分析认为 24×5=120，120 小于 168，24×10=240，240 大于168，所以168÷24的商肯定在6-9之间。其中有2人在此基础上运用乘除法的互逆关系，笔算了24×6，24×7，24×8后，得出168÷24=7。（4）有7人用旧知类比新知，将除数是两位数除法转化成除数是一位数除法进行计算，先用168÷6=28，再算28÷4=7。（5）有9人直接用竖式计算168÷24=7，完全正确的7人，商的位置书写有误2人，其中有7人的竖式中能清楚看出调商的过程，访谈这部分学生有家长教过或在补课班学过的经历。

由前测可见，“除数是两位数笔算除法的试商方法”，是需要在学习过程中重点讨论的；而借助除数是整十数的口算、估算学习，获得用“四舍五入法”进行除数非整十数试商的经验迁移；通过除数是一位数，商两位数的计算体验理解除数是两位数、商也是两位数除法的算理、实现笔算方法的同化也同样重要。

2.学生认知特点解读。

瑞士心理学家皮亚杰曾经说过：“儿童是在与周围环境相互作用的过程中，逐步建构起关于外部世界的知识，从而使自身认知结构得到发展”。也就是说，学生是在将原有认知与现实问题不断关联的过程中，逐渐构建新知的。

结合小学阶段整数除法运算的知识结构，学生在三年下已经掌握了“除数是一位数的除法”的算理、算法，当出现“除数是两位数的除法”这个新知时，学生能借助已有经验把新知的解决方法纳入到旧知中，这是学生认知发展中的“同化”现象。这一现象中加速实现新旧知识转化的正是“类比迁移”的思想方法。在“同化现象”和“类比迁移”思想方法的相互作用下，学生会逐渐打通本单元的知识体系，在自我学习、自我反思、自我认识中构建起整数除法运算的同法通则。为今后进行更多数位的整数除法运算及后续小数除法运算等做好持久性学习准备。

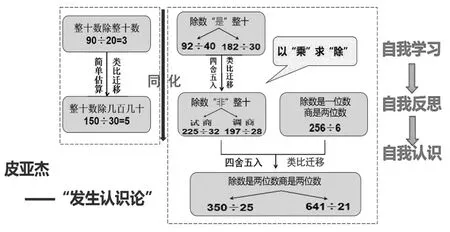
单元整体类比迁移图

3.制定单元TUKE目标。

“大观念引领”的单元教学，就学习目标而言，不仅包括知识技能目标，（简称K目标），更为重要的是依据具体观念设定的思维迁移目标（T目标）和意义理解目标（U目标）。同时，我们还关注到“情感态度”在学习活动中的推进作用，补充了情感态度目标（E目标）。

基于学情评估和学生认知特点的分析，围绕单元具体观念，确定了本单元的TUKE目标。如下：

4.形成学生思考的关键问题。

学生思考的关键问题可以是教师在对学情充分评估的基础上为实现理解意义和自主迁移目标而设定的问题，也可以是来自于学前调研中学生感兴趣或困惑的问题。无论哪一类问题都和学生先期的学习基础和经验紧密联系。针对目前课堂教学中普遍存在的教师设问随意、细碎、缺乏整体的问题，我们在研究中提炼出指向和突出本单元具体观念的关键问题如下：