棒球击球点问题
李 晨 陈玉松
(商丘工学院基础部 河南 商丘 476000)
一、问题重述
棒球击球时,球棒较宽的那部分有一个“最佳点”,使用该点击打球时传给球的力量是最大的。问题来了,这个位置为何不是击球棒的最外端?从力学的角度分析,似乎用击球棒的最外端击球,球得到的力量是最大的,但结合实际经验,这显然是不对的。所以,本文要研究的问题如下:
其一:建立模型来解释这一问题。其二:建立模型阐述不同材料(分木制和铝制两种情况)的击球棒对这个“最佳点”的影响。
二、问题分析
“棒球击球”是一个极具代表性的碰撞问题。本文目的是构建模型解释“最佳点”为何不在球棒最外端。
我们首先需要明确的一个问题是“最佳点”的具体含义。击球的过程中我们将力量能最大限度地转移到球上的位置称为击球点的“最佳点”。由于力的转移很难量化,而球初始速度却可以测量。这样,求“最佳击球点”的问题就变成了求球的初始速度最大的击球点问题。现有研究表明:碰撞瞬间手对棒施加的力对棒初始速度的影响并不大,所以可理想认为球棒是“自由端”。结合动量守恒定理、角动量守恒定理、恢复系数来研究碰撞位置与球初始速度的关系从而找到“最佳点”。
第二个问题,棒的材质之间的区别主要有:因密度和质量的不同所导致的转动惯量的不同;因材料的不同所导致的恢复系数的不同;弹性系数的不同进而影响到击球效果的不同。
三、模型假设
1.球在运动过程中不会出现偏转、旋转、掉落等事情的发生;
2.球、棒均视为刚体;
3.在击球的过程中正好击中球的中心,不存在侧击的情形;
4.击打过程中忽略外部其他作用力(比如空气等);
5.击球时,球的速度方向与球棒轴线正交;
6.球棒是“自由端”;
四、符号说明
e:恢复系数;C:重心位置;J:转动惯性;M:棒球质量
五、模型的建立与求解
(一)球棒外形的抽象描述模型
木质的棒球球棒的规格一般为:棒长L=0.855m;棒重M=0.885kg;木质密度ρ=649kg/m3;木质杨氏模量E=1.814*1010N/m2;最大半径r2=7cm;最小半径r1=2.5cm。
以球棒做为一种旋转体,沿轴线的截面如图1所示:

图 1
其中每一部分的长度x1、x2可由球棒的重量和重心的位置确定:
球棒重量:
(1)
根据质心的定义,质心两侧的球棒所承受的重力对重心力矩平衡:
Mgl=Mgr
(2)
由(1)(2)式,带入数据得:x1=0.346,x2=0.642
这样,棒球各部分的半径长:r1=0.025,r2=0.070
棒球球棒的外形简化模型的确定,使得不同的材质及材质不均匀的球棒转动惯量的求解变得更方便。
(二)最佳击球点的刚体动力学模型
力学模型如图所示:
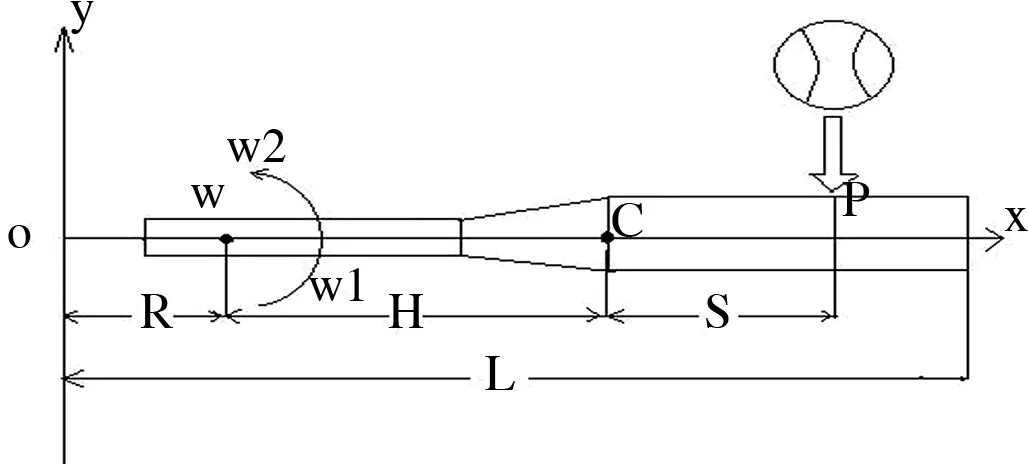
图 2
各符号表示如:m1:球的质量,m2:球棒的质量,v1:球初速度,v2:球离开速度,u1:击球前的质心速度,u2:击球后的质心速度,w1:棒击球前的角速度,w2:棒击球后的角速度。
在碰撞瞬间,球与棒之间的作用力远远大于球的重力、棒的重力、手的支持力,因此,以球-棒整体为研究对象,y轴方向上的动量守恒:
m1v1+m2u1=m1v2+m1u2
(3)
u1=ω1(R+H),u2=ω2(R+H)
(4)
恢复系数e是碰撞后相对远离的速度与碰撞接触点碰撞前相对接近的速度的比,即:
(5)
以身体的重心轴为轴建立以球-棒为系统的角动量守恒方程和以球棒的质心为轴建立以球-棒为系统的无外力矩,因此角动量是守恒的,即:
m1v1(S+R+H)+Jω1=m1v2(S+R+H)+Jω2
(6)
由(3)、(4)、(5)、(6)可得击打后的球速表达式为:
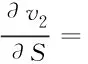

计算得“最佳点”为距球棒手柄端点70cm处。
(三)球棒材料的不同对击球效果的影响
金属球棒与木质球棒的主要区别有:①不同的密度和质量导致转动惯量的不同;②不同的材料导致恢复系数和弹性系数的不同。
利用力学的经典理论模型,假设前面的抽象模型与两种球棒的外形相同,从转动惯量和恢复系数的角度来研究两种材质球棒的性能,建模结果显示,用铝棒击球比用木棒更容易打出而且球飞得又高又远。
六、结果分析
1.优点:(1)对球棒外形进行抽象简化,使研究对象易于描述与建模。(2)利用理论力学、接触力学、波动力学等多种理论对球-棒碰撞这一问题从外部表现到内部机理进行了多角度的分析。
2.不足之处:利用各分支学科的各个力学理论建立起来的模型是互相独立的,但却没有分析各模型之间存在的关系。

