基于自适应参数调节和动态分组学习的水波优化算法*

林伟豪，何杰光，肖佳嘉

(广东石油化工学院 计算机学院，广东 茂名 525000)

郑宇军提出基于浅水波理论[1,2]的水波优化算法(WWO)，该算法模拟水波运动中存在的传播、反射、碎浪等运动，且在旅行商问题和车辆路径[3]问题得到了较好的应用。张蓓等[4]分析了WWO执行传播和折射操作时的收敛情况，并验证了上述两种情况的收敛条件。杜兆宏等[5]提出自适应碎浪系数调整策略来平衡算法的全局勘探和局部开发能力。顾启元等[6]采用双种群进化结构维持种群多样性并提高个体学习效率。综上，可以看出WWO在收敛速度和收敛精度上仍具有较大的改进空间，基于此本文提出了基于自适应参数调节和动态分组学习的水波优化算法(DGLWWO)。DGLWWO以非线性变化的碎浪系数来平衡算法的搜索机制，并设计了基于正余弦因子的动态分组学习阶段，主群与子群的信息交流机制使算法在进化后期仍有找到最优解的可能。

1 原始水波优化算法

1.1 传播

(1)

λ=λ·α-(f(X)-fmin+ε)/(fmax-fmin+ε)

(2)

式中：α为波长衰减系数；fmin和fmax分别为最优和最差的水波；ε为一个很小的正数。

1.2 折射

当水波波高h递减为零时，按式(3)执行折射操作，并将波长重置为h=hmax。

(3)

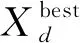
1.3 碎浪

(4)

2 基于自适应参数调节和动态分组学习的水波优化算法

2.1 碎浪系数β的自适应调节

碎浪系数β控制在最优水波附近密集搜索孤立波的范围，β越大，搜索范围越大，全局搜索能力越强。WWO的β随迭代次数的增加而线性递减，无法很好地平衡算法前期的全局搜索能力和后期的局部开发能力。基于此，本文设计了正弦变化的碎浪系数β，其表示为

(5)

图1 自适应碎浪系数

WWO和DGLWWO的碎浪系数如图 1所示，DGLWWO在进化前期保持较大的碎浪系数，有利于支持算法的全局搜索，特别是在求解多局部最优值问题时，一定程度上提高了找到其他更优解的概率。而随着迭代的进行，碎浪系数迅速减小，使算法能够进行更多的局部精细开发。

2.2 基于正余弦因子的动态分组学习阶段

为了解决WWO种群后期进化缓慢的问题，本文设计了基于正余弦因子的动态分组学习阶段。其动态分组策略过程主要是，随机从[2,10]内选择分组规模M，分成Np/M个分组，当Np%M≠0时，最后一个分组规模为M+Np%M。动态分组学习阶段可表示为

(6)

(7)

式(6)中，水波以正弦方式向组内最优个体靠近，在全局范围内搜索，并维持种群多样性。式(7)中，水波以余弦方式向全局最优个体靠近，进行局部开发，加快算法收敛。正弦全局搜索能够有效弥补余弦局部开发而导致陷入局部最优的缺陷，而余弦局部开发提高了算法的寻优性能。由此可知，动态分组学习促进了个体之间的信息交流，这在避免算法早熟、提高收敛精度的同时，提高了算法的求解效率。

2.3 DGLWWO实现流程

DGLWWO的执行步骤如下：

(1)随机生成一个规模为Np的种群，并计算每个水波的适应度值，找到最优水波；

(2)按式(1)～(5)，对每个水波执行传播、折射、碎浪操作；

(3)动态分组，随机选择分组规模M，生成Np/M个分组；

(4) 按式(6)、式(7)，执行动态分组学习阶段；

(5)更新每个水波的波长，并计算每个水波的适应度值，求得全局最优解；

(6)若满足结束条件，则输出全局最优解；否则，执行(2)。

3 仿真实验与分析

3.1 测试函数及参数设置

为验证DGLWWO的有效性和稳定性，选取10个标准测试函数进行测试，并与原始WWO算法[1]、LOGWWO算法[5]、ACLWWO算法[6]、S-WOA算法[7]进行对比。测试函数及其特性，结果见表1。所有算法的最大迭代次数设置为1000，每个算法独立运行20次，问题求解空间的大小D为30。WWO、LOGWWO、S-WOA、DGLWWO的种群规模均为10，WWO、LOGWWO、DGLWWO的波长λ=0.5、波高hmax=12、碎浪系数的最大值和最小值分别为βmax=0.250和βmin=0.001、波长衰减系数α=1.0026；ACLWWO的参数来源于文献[6]，主种群和子种群规模均为20，子种群波高为hmax=100，波长衰减系数α=1.0260。

表1 标准测试函数

3.2 基于正余弦因子的动态分组学习阶段有效性验证

为了验证基于正余弦因子的动态分组学习阶段的有效性，构造4种不同的算法进行对比性实验，分别是DGLWWO、DGLWWO-DGL(不使用动态分组阶段)、WWO和WWO+DGL(加入动态分组学习阶段)。选用f5作为测试函数，f5是一种极难搜索全局最优解的病态非凸单峰函数，适合用于测试算法的收敛性。4种算法分别在f5上独立运行20次，结果如表2所示，平均收敛曲线如图2所示。

表2 4种算法分别在f5上的收敛性

a 动态分组学习阶段的收敛过程 b 动态分组过程的稳定性

由表2可知，DGLWWO和WWO+DGL表现出更好的收敛精度，这说明动态分组学习阶段有利于增强种群多样性，提高算法的寻优能力。由图2可以看出，DGLWWO和WWO+DGL的收敛速度明显优于DGLWWO-DGL和WWO，虽然4种算法都较早地陷入了局部最优，但对比WWO和WWO+DGL的稳定性可知，动态分组学习阶段在提高收敛精度和收敛速度的同时，能够有效保证算法的稳定性。综上所述，动态分组学习阶段有效地避免了算法过早丢失多样性，提高了算法的收敛精度和收敛速度。

3.3 实验结果及分析

各算法的平均收敛曲线如图3所示，收敛结果如表3所示。

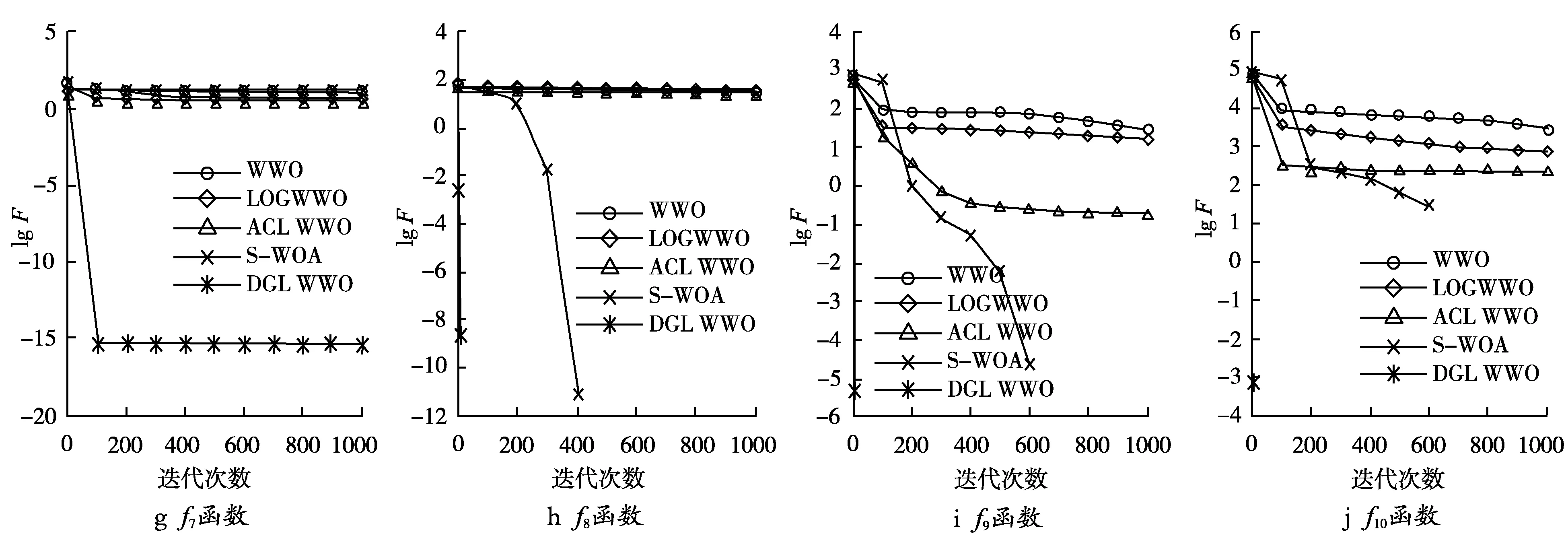
图3 算法平均收敛曲线情况

表3 各算法收敛结果

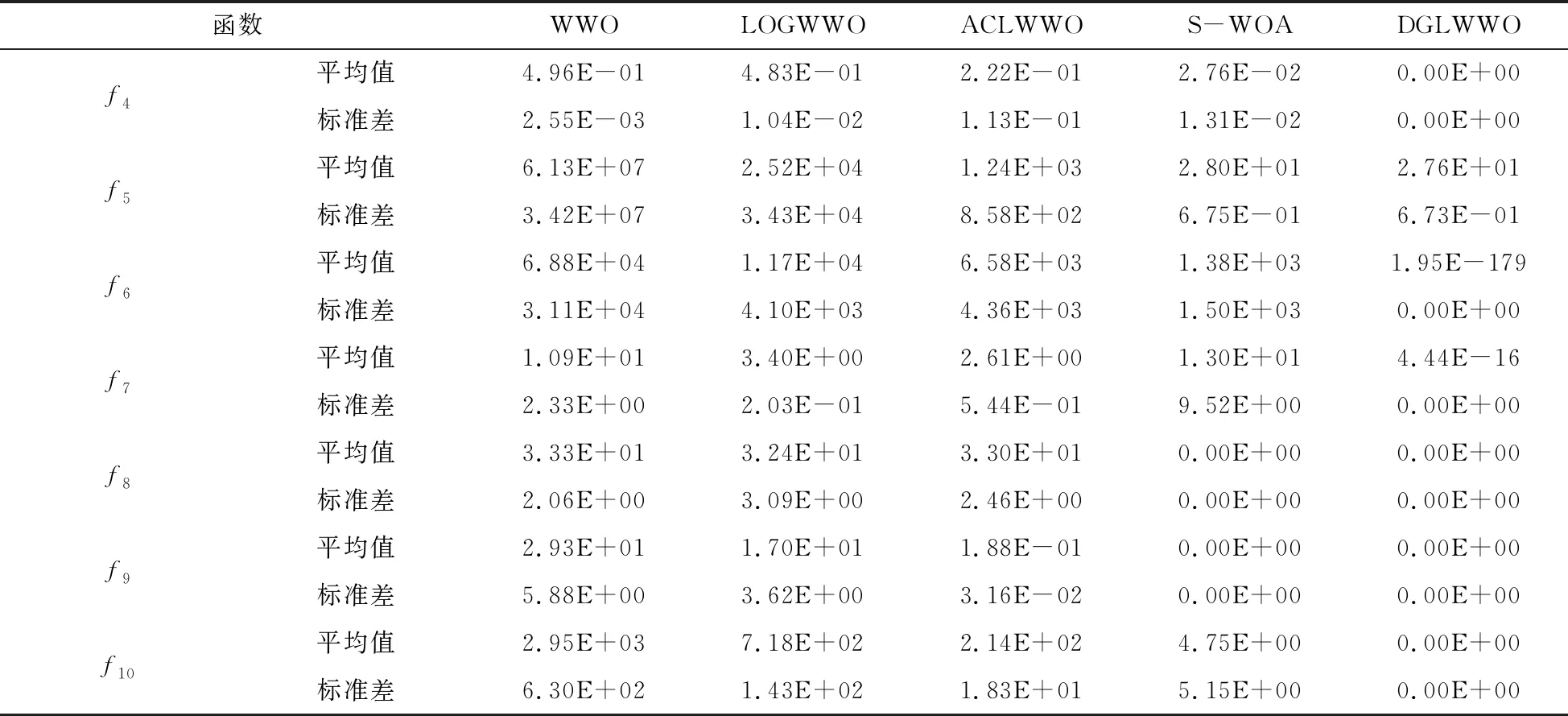
续表

由图3可知，函数f1～f6的收敛速度明显优于其他算法，函数f1～f3迭代200次就已寻得理论最优解；函数f4求解时能迅速收敛并找到最优解；与其他算法相比，函数f5和f7在小于200次迭代时就已寻得较好的精度，但随之出现了进化停止的现象；函数f6在小于400次迭代时收敛速度较快，在进化后期仍能表现出较好的寻优能力，能够进一步提升收敛精度；函数f8～f10在小于50次迭代就已求得最优解，说明DGLWWO在求解复杂问题时更具优势。

由表3可知，DGLWWO的收敛精度均优于其他算法，其中对函数f1～f4均能求得其理论最优解；函数f5～f7虽然没有求得最优值，但其求解精度分别至少提升了2个、176个和15个数量级，并且获得了最小的标准差；对复杂多峰函数f8～f10均求得理论最优解。这说明，DGLWWO在收敛精度和稳定性方面表现出较好的竞争性。

综上，基于正余弦因子的动态分组学习阶段使DGLWWO在进化后期仍能保持较好的种群多样性，仍具有找到更优解的可能，有效地协调了算法进化前期的全局探测能力和后期的局部开发能力。此外，碎浪系数的自适应调节对于提高DGLWWO的优化性能提供了一定的帮助。

4 结语

本文针对WWO存在的缺陷，提出了基于自适应参数调节和动态分组学习的水波优化算法DGLWWO。DGLWWO设计了基于正余弦因子的动态分组学习阶段，主群与子群的信息交流机制和动态变化的分组策略，有效地避免了种群过早丢失多样性，同时提高了算法后期仍能进化的概率。实验表明，DGLWWO保持了WWO的优点，同时极大地提高了WWO的优化性能。