基于ASIFT改进算法的无人机图像特征匹配方法研究

孙东阁, 陈 辉

(上海电力大学 自动化工程学院, 上海 200090)

近年来,无人机因其机动性强、成本低等优点在军事和民用领域得到了广泛应用[1]。但目前通过无人机航拍对物体进行非接触信息采集来构建物体的三维模型,在考古、信息化城市、文物保护、机器人、军事等领域应用还不够成熟。因此,研究无人机图像处理技术具有重要现实意义[2]。特征匹配是指在一个被测目标的两幅或多幅图像中寻找相同的特征点,探寻其对应关系,从而将这两幅或者多幅图像进行匹配的过程。无人机图像的特征匹配在军事、人工智能、图像拼接、三维重建、物体追踪及定位领域中的应用十分广泛[3]。

随着计算机技术的不断发展,无人机图像匹配算法也得到了不断改进。1988年Harris算子的提出[4],增加了特征点的稳定性,但其对边缘点的检测仍然不够敏感。1999年,LOWE D提出了尺度不变特征变换(Scale-Invariant Feature Transform,SIFT)算法[5]。该算法经不断完善,在图像匹配中得到了广泛应用,但其仍存在不足之处,如计算复杂,在视角变化大、纹理丰富的无人机图像匹配中难以获得匹配对等[6]。2006年ECCY大会上提出的加速稳健特征(Speeded Up Robust Features,SURF)算法,在一定程度上提高了匹配速度,但对于视角变化的处理仍不够理想[7]。2009年,MOREL J M等人提出ASIFT(Affine-SIFT)算法[8],相较之前的算法,提高了匹配效率。近年来,不断有学者对ASIFT算法的相机模型[9]进行了改进,增加了匹配数量,但在匹配过程中存在误差匹配较多等问题。基于此,本文提出了一种ASIFT改进算法,以解决原算法中存在的误差匹配问题。

1 特征提取

1.1 SIFT算法

SIFT算法主要包括提取、描述、匹配3个步骤。首先,在DoG金字塔尺度空间内提取特征点。尺度空间由高斯卷积、图像下采样和高斯差分操作构建而成。在尺度空间中初步提取出作为局部极值点的兴趣点,再剔除掉能量低的不稳定的和错误的兴趣点,得到最终稳定的特征点[10]。然后,设定特征点的主方向,便于对特征点进行描述,旋转特征点的方向来构造特征描述子,可以使算子保持较好的旋转不变性。特征点的主方向可以借助其邻域像元的梯度分布情况来描述[11]。

为了实现图像旋转的不变性,以关键点为坐标原点,将坐标轴旋转为关键点的主方向,然后以关键点为中心,取8×8个邻域作为采样窗口。通常一个特征点由2×2共4个种子点组成,形成2×2×8共32维描述子。为了提高匹配的稳定性和鲁棒性,对每个特征点采用 4×4 共16个子区域进行描述,即16个种子点。每个区域分为8个方向,即形成一个16×8共 128 维 SIFT 特征描述子。然后对特征描述子数据进行归一化处理,进一步减弱灰度变化带来的干扰。

最后,利用k-d树在高维空间快速而准确地找到查询特征点的近邻,用欧式距离作为相似性度量,即特征向量的最近邻与次近邻的比值进行匹配。取参考图像中的任一特征点,找出其与待配准图像中距离最近的两个特征点,如果最近邻值与次近邻值的比值小于设定阈值,则认为该匹配对为正确匹配对,否则判为误匹配对。特征点匹配实际上就是一个通过距离函数在高维矢量之间进行相似性检索的问题。

1.2 ASIFT算法

SIFT算法在传统图像配准中可以取得很好的效果,但是在面对视角变化较大、纹理较为丰富的无人机图像时,往往只能找到少数特征点甚至不能匹配[12]。ASIFT算法是基于SIFT算法提出的一种改进算法。ASIFT算法提出经度、维度的概念,通过模仿相机的实际位置,从而估测由相机位置不同而产生的图形畸变[13]。一个完整的仿射矩阵需要6个参数,SIFT算法模仿其中4个:相机围绕光轴的旋转、相机焦距、平移和旋转。ASIFT算法则模仿2个参数:相机与图像法线的倾斜角θ和旋转角φ,即为相机模型的纬度角θ和经度角φ。仿射相机模型如图1所示。图1中:α代表图像平面;φ为相机光轴经度;θ为相机光轴纬度;ψ为相机旋转;λ为对应缩放。

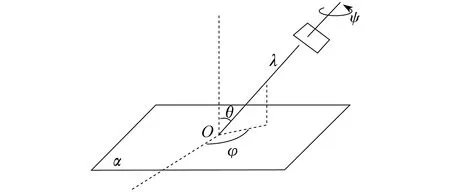
图1 仿射相机模型

ASIFT算法匹配直观图如图2所示。图2中,A代表参考图像,B代表模拟图像。由图2不难看出,图像B是由图像A进行小幅旋转得到的。

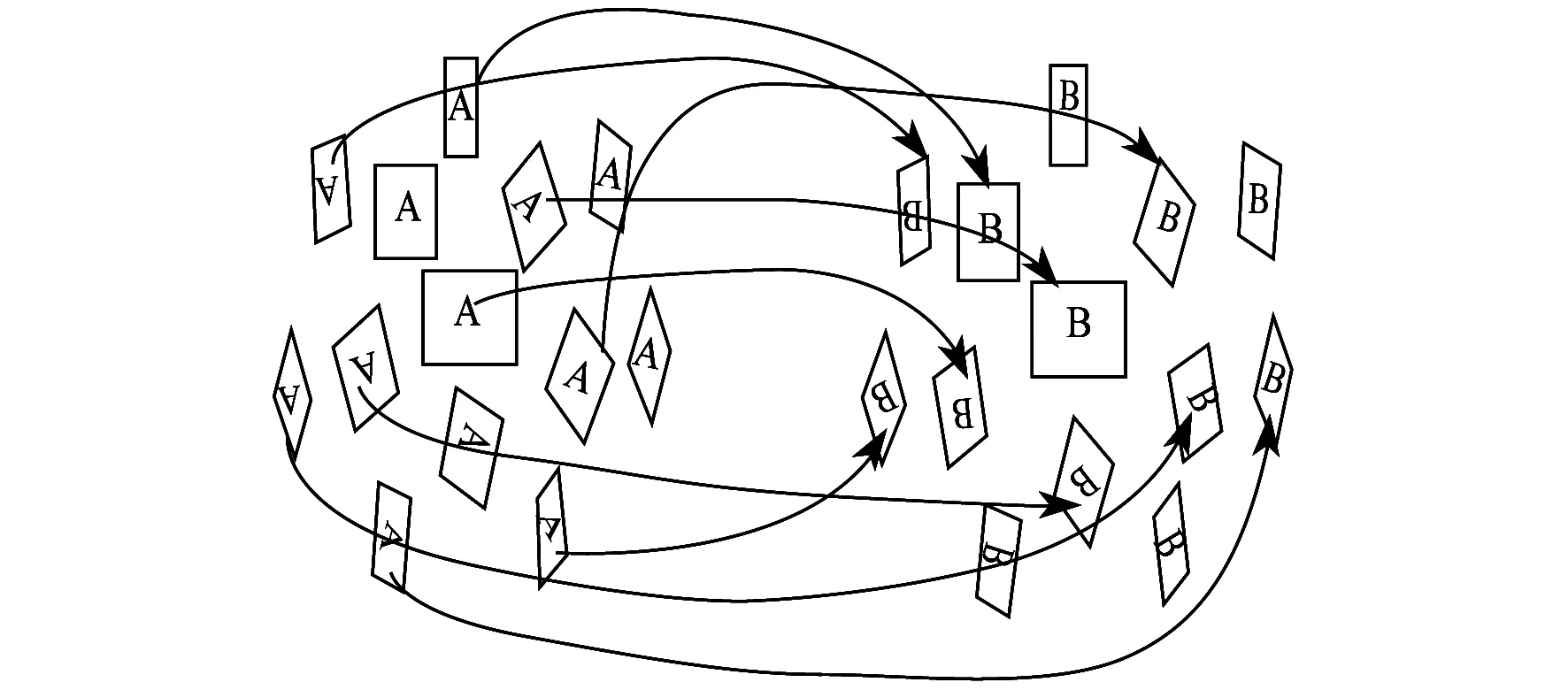
图2 ASIFT算法匹配直观图

2 基于ASIFT的无人机图像匹配

2.1 算法流程

本文以两幅图像作为输入图像;利用ASIFT算法建立相机模型,进而模拟图像畸变;然后采用SIFT算法进行特征点的提取与匹配;最后加入随机抽样一致(Random Sample Consensus,RANSAC)算法[14]对误差匹配进行剔除。其整体流程如图3所示。

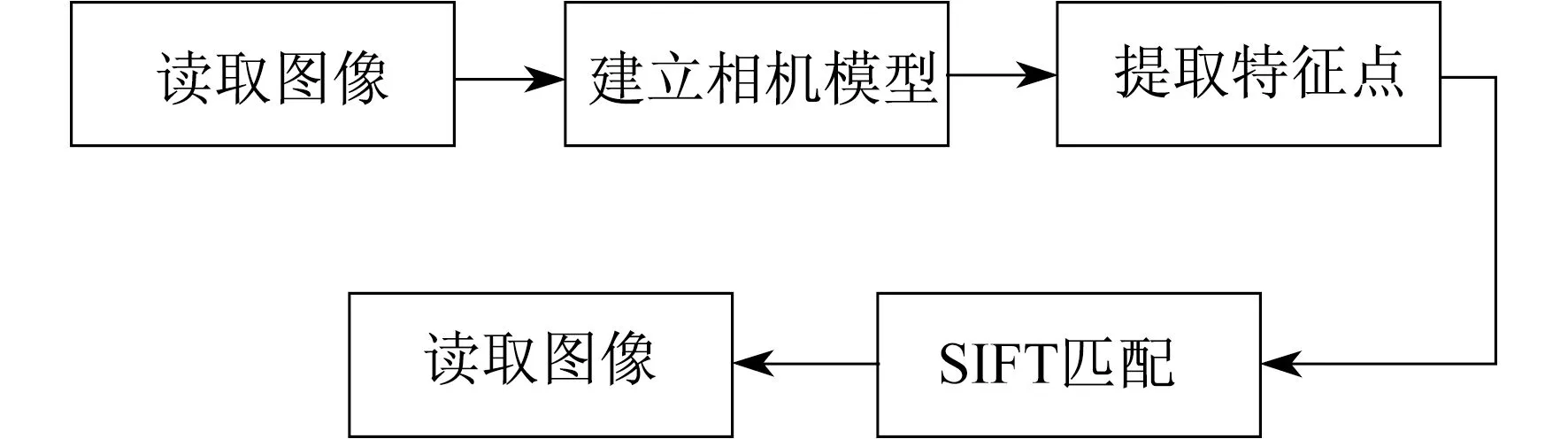
图3 算法流程示意

具体如下。

(2)采用SIFT算法对模拟图像I′(φ,t)提取匹配。在尺度空间进行表示:

(1)

L(φ,t,σ)=G(φ,t,σ)*I′(φ,t)

(2)

式中:G(φ,t,σ)——高斯核函数;

σ——尺度空间因子;

L(φ,t,σ)——图像的尺度空间;

*——卷积运算。

首先通过差分金字塔D(φ,t,σ)的构建来实现特征点定位,然后利用邻域像元的梯度分布来描述特征子的方向,最后采用k-d树算法用欧式举例作为相似性度量,即特征向量的最近邻值与次近邻值的比值进行匹配。

(3)

2.2 误差剔除

取参考图像中任一特征点,找出其与待配准图像中距离最近的两个特征点。如果最近邻值与次近邻值的比值小于设定阈值0.8,则认为该匹配对为正确匹配对,否则,判为误差匹配对。对于误差匹配,本文采用RANSAC算法,其原理是根据一组包含异常数据的样本数据集,计算出数据的数学模型参数,从而得到有效样本数据。

RANSAC算法的核心思想就是在匹配的特征点中随机抽取4个特征点,通过计算和不断迭代,寻找到最优的参数模型,在这个最优模型中,能匹配上的特征点最多。

引入最优单应性3×3矩阵H,使得满足该矩阵的匹配特征点最多。令h33=1来归一化矩阵,H只有8个未知参数,对应到特征点位置信息上,至少需要4组特征匹配点对才能求解得到单应性矩阵H。

(4)

式中:s——尺度参数;

(x′,y′)——模拟场景图像中的角点位置;

(x,y)——目标场景图像中的角点位置。

RANSAC算法从匹配数据集P中选出随机样本S,初始化模型M,然后利用该模型测试所有数据,并计算满足该模型数据点的个数与投影误差(即代价函数)。若该模型为最优模型,则对应的代价函数最小。计算代价函数的公式为

(5)

3 实验结果与分析

为了验证算法的有效性,本文采用大疆无人机精灵4 PRO P4P,以校园环境中的建筑物为目标进行实验,所采集的每幅图片的尺寸规格均为800×600。实验在Visual studio 2013 Open CV软件环境下,运行于Windows 7操作系统的计算机上。编程语言为C++。首先利用ASIFT算法对实验图像进行特征点提取,然后对提取的特征点通过k-d树算法进行快速匹配,最后用RANSAC算法训练建立模型,以此来不断筛选出最优匹配,达到剔除误差匹配的效果。

甸园锦江宾馆、上海电力大学科技园、上海电力学院图书馆分别在SIFT算法,ASIFT算法,ASIFT改进算法下的匹配结果如图4、图5、图6所示。

图4 甸园锦江宾馆在3种算法下的匹配结果

由图4～图6可知,在同一无人机图像对的匹配中,ASIFT算法匹配对数远远超过SIFT算法。此实验结果说明ASIFT算法在无人机图像匹配中效果远好于SIFT算法。但从图4(b)、图5(b)、图6(b)可以看出,ASIFT算法下的匹配结果仍存在诸多错误匹配,因此我们在此基础上进行了改进,在ASIFT算法上加入 RANSAC算法,由图4(c)、图5(c)、图6(c)可以看出,加入该算法后,匹配对相应减少,消除了错杂混乱的匹配现象。

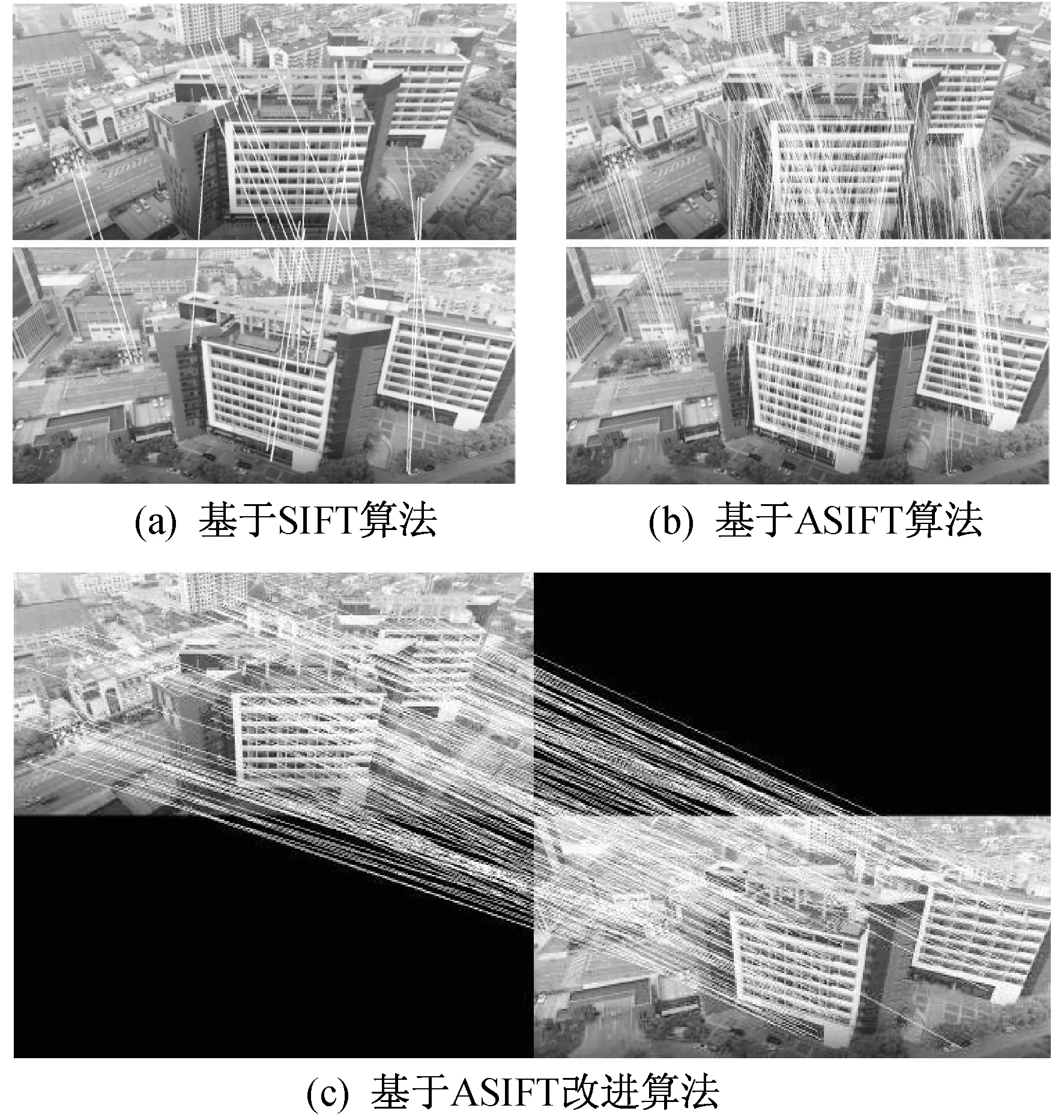
图5 上海电力大学科技园在3种算法下的匹配结果

图6 上海电力大学图书馆在3种算法下的匹配结果

3种算法下的匹配结果数据如表1所示。3种算法下的匹配时间数据如表2所示。

由表1可知,在同一无人机图像匹配中,采用ASIFT算法所得匹配对数约为SIFT算法匹配对数的20倍,其效果远好于SIFT算法;采用ASIFT改进算法对误差匹配进行剔除后,其匹配对数则约为SIFT算法匹配对数的7倍。由表2可知,ASIFT算法匹配时间长于SIFT匹配算法,ASIFT改进算法匹配时间介于ASIFT算法与SIFT算法之间。因此,相较于ASIFT算法,ASIFT改进算法匹配速度约提升了23%;相较于SIFT算法,ASIFT改进算法时间差距较小,而匹配能力远远优于SIFT算法。

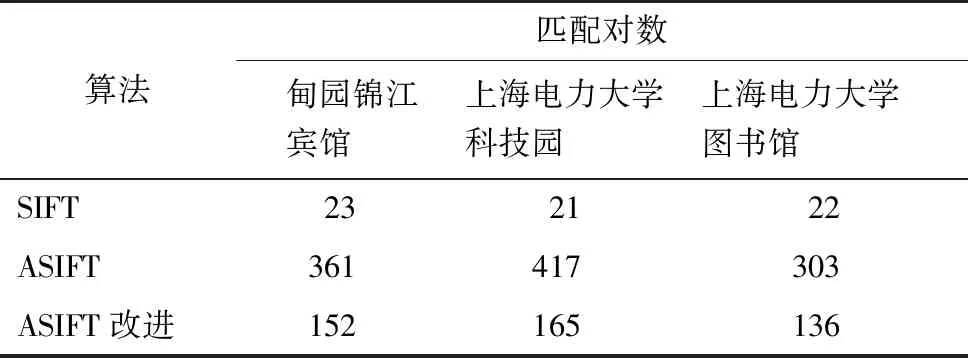
表1 算法匹配结果对比 单位：对

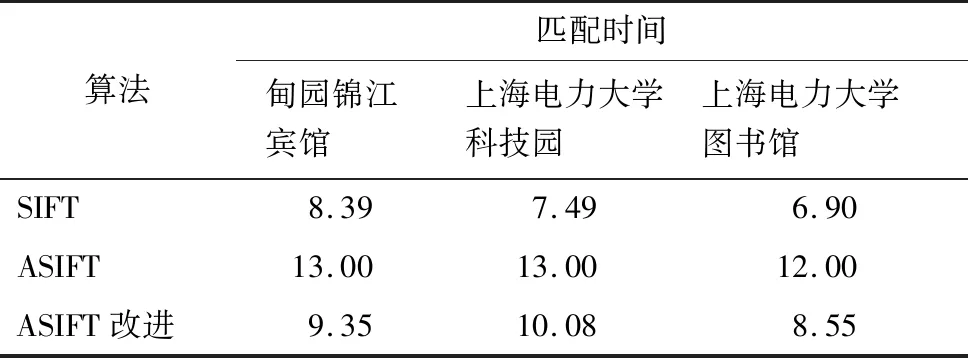
表2 算法匹配时间对比 单位：s

4 结 语

本文所提算法是基于ASIFT算法的一种改进算法,该算法保留了ASIFT算法的特征提取部分,以及SIFT算法的特征点匹配部分,并在此基础上加入了RANSAC算法,对ASIFT算法进行误差匹配的过滤,以优化匹配效果。通过对甸园锦江宾馆、上海电力大学科技园、上海电力大学图书馆3个场景进行无人机图像的采集,采用3种算法对匹配结果进行对比,最终得出符合预期的实验效果。对实验证明,本文所提改进算法可以有效剔除ASIFT算法中的误差匹配,并且提高了约23%的匹配速度。