基于智能手机的静电场描绘及模拟
林春丹 李秋真 张 程 张万松 杨振清
(中国石油大学(北京) 1理学院; 2新能源与材料学院,北京 102249)
2020年以来,受新型冠状病毒肺炎影响,教育部明确要求各高校延迟开学,以“停课不停学”为目标,组织开展线上教学,指导学生居家学习[1]。线上教学一般需要手机的辅助,小巧的智能手机变成必不可少的工具,尤其对于处理比较繁琐的物理实验数据也可以用智能手机辅助完成,因此引导学生在学习中尝试利用智能手机对提高线上实验教学效果有较好的作用。本文针对用模拟法描绘静电场这一理工科学生必做的基础实验[2]展开研究。由于静电场难以直接准确测量,通常利用电流场来模拟静电场。实验中一般采用双层静电场测试仪,通过探针在纸上打出电位相等的点[3-4]。实验中数据处理的一个重要环节是测量各等势线的半径,并对U与lnr进行线性拟合[5]。传统上一般由学生手动计算出半径的平均值,并拟合U与lnr的线性关系,得出斜率值。此过程涉及的数据处理量大,计算过程复杂,且耗时较长。其他运用OpenCV软件[6]、Origin软件[7-8]、Matlab软件[9-10]等计算机软件进行数据处理的方法对学生的编程或软件运用能力要求高,不易上手。同时,此类软件安装困难且计算机不便携带。这使得静电场描绘实验的数据处理过程具有一定的难度。
由此本文提出了基于智能手机中的相机及Geogebra软件完成实验数据处理的方法。利用Geogebra软件实现了等势点的坐标确定、等势线的拟合、三维等势面的模拟等过程。此方法可大幅减小实验数据的处理难度,节约学生们的计算时间。同时,智能手机的普及和Geogebra软件的开源性使得此方法具有较强的普适性,适合在疫情期间进行居家学习。
1 静电场描绘实验的原理及内容
1.1 用电流场模拟静电场
静止电荷产生的电场称为静电场。然而,由于静电场中无电流,无法用常见的电流表进行测试。静电式仪表又存在静电感应的问题,会改变电场的原始分布,因此静电场很难直接测量[8]。
恒定电流所产生的稳恒电场的基本特性与静电场相同,且其中的电场分布容易测量,故可用恒定电流场来模拟静电场[11],即通过测量和描绘电流场中的电位分布来确定相应静电场中的电位及场强分布。
1.2 真空中的圆柱形电容器
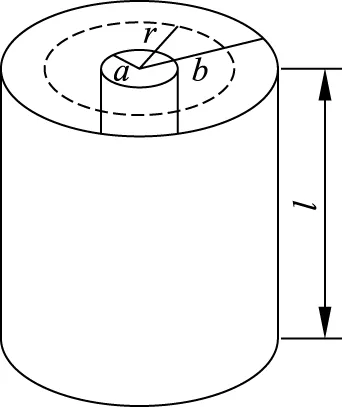
图1 圆柱形电容器示意图
本文主要针对两个长直同轴圆柱型导体间的电场[12]进行研究。设长为l的圆柱形电容器(图1)的内外极板的半径分别为a和b(且a、b≪l),设其均匀带有等量异号的电荷,线电荷密度的绝对值为λ。由于其对称性,半径为r(r>a)的圆柱面上电场强度的方向应沿着半径方向,大小E应为常数,则由高斯定理可得:
(1)
令U为内圆柱面与半径为r的圆柱面上一点p之间的电压,则:
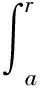
(2)
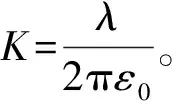
1.3 等势线的测定与描绘
测量二维电场电位分布的实验装置示意图如图2所示,电路图如图3所示。装置下部的电极间充以导电液P,在内外电极之间加上频率为1000Hz的交流电,电压有效值为U0。在两电极间有电流流过,从而形成一组等势线,其位置可通过电压表和探针e测出[13]。

图2 实验装置示意图
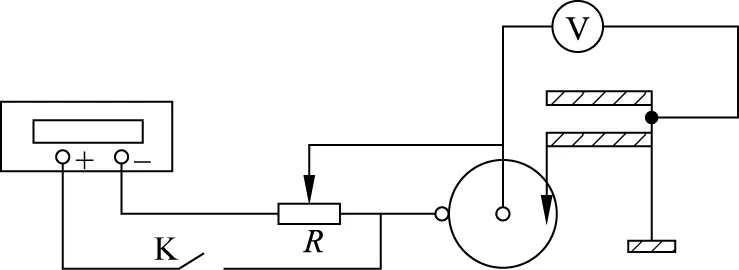
图3 电路示意图
实验步骤如下:
(1) 按图3连好线路图,在电极水槽中充以适量的水作为导电液,水的深度以稍没过电极为宜。
(2) 接通电源,通过调节电源的输出电压和滑线电阻的分压使两电极间的交流电压有效值为1.00V。
(3) 打出电压表读数为0.20V、0.30V、……、0.90V的几组相差为0.10V等势点。
(4) 将各等势点连接,描绘出等势线。
1.4 电力线的描绘
在静电场中,电场强度矢量等于电位的负梯度。当画出电场等势线的分布图后,就可在此基础上描绘出电力线图,在描绘时使电力线与等势线处处垂直,且电力线的方向指向电位下降的方向。
2 人工数据处理
2.1 人工数据处理流程
静电场描绘实验的传统数据处理方法需要学生手动描点、测量并计算。处理步骤如下:
(1) 将各等势点连接绘制出等势线,垂直于等势线绘制电场线,确定圆心。图4为学生手动描绘的等势线及电场线图。

图4 手描的等势线图
(2) 在各等势线中取四个点进行半径的测量和记录,并计算半径的平均值及对数值。实验数据的记录与计算结果如表1所示。
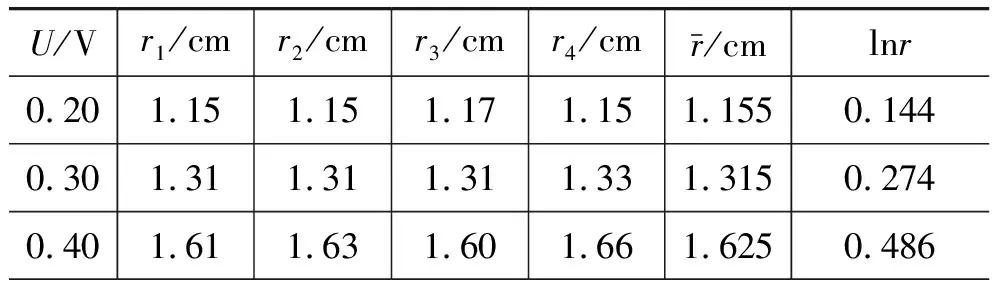
表1 各等势线的半径值、半径平均值及对数值
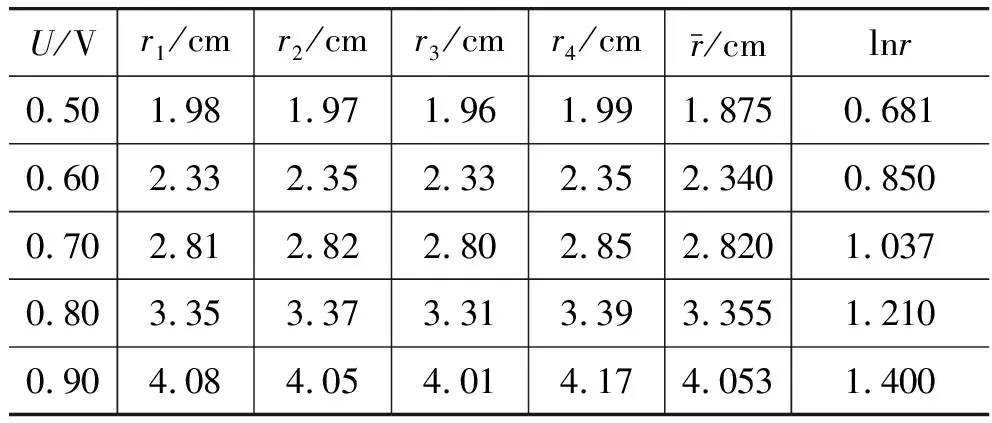
续表
(3) 在坐标纸上建立U-lnr坐标系,描点作图并进行拟合, 拟合曲线如图5所示,该曲线符合线性关系,计算得到斜率为0.55。

图5 人工线性拟合图
2.2 人工数据处理的弊端
人工数据处理过程涉及大量的数据测量、记录和计算过程,处理过程复杂且耗时。且人工绘图和确定圆心的过程存在较多不确定因素,计算过程中也存在精度的限制,带来了一定的实验误差,难以保证实验的准确性。
3 基于智能手机的实验数据处理
3.1 Geogebra软件的简要介绍
Geogebra,简称GGB,是一款免费、开源且性能可靠的学习和教学的动态软件[14]。它包含运算区、绘图区、表格区等多个模块以及代数、几何、统计等多项功能。其数学表现丰富准确,且界面简洁,操作方便,易学易用,占用内存小,学生可独立完成安装及操作过程。
3.2 基于智能手机的数据处理
3.2.1 打点图的导入及定位
利用智能手机中的相机,1∶1拍摄打点图。将拍摄图片导入手机中的GGB软件,根据实际打点图中最外侧等势线的直径值(单位cm)设定图片的顶点位置,使图形的像素坐标与实际坐标吻合。将图片锁定于坐标轴之上,则其在后续缩放或移动过程中会与坐标轴同步变化。
3.2.2 点的标定及图像模拟
利用“标点”工具,可得到各点的坐标值。在每圈等势线上选取连线接近正三角形的点进行标定,以保证圆心位置误差及其对应的半径标准差均为最小,即为“优质组合”[5]。标点过程中可将图片进行放大并调整有效数字位数以保证标点的的准确性及精确度。在最内圈标出三点A、B、C,可自动显示其坐标。利用“圆形拟合”工具,可得到最内侧圆形的方程式及r2值。点的坐标及拟合结果如图6(a)、(b)所示。
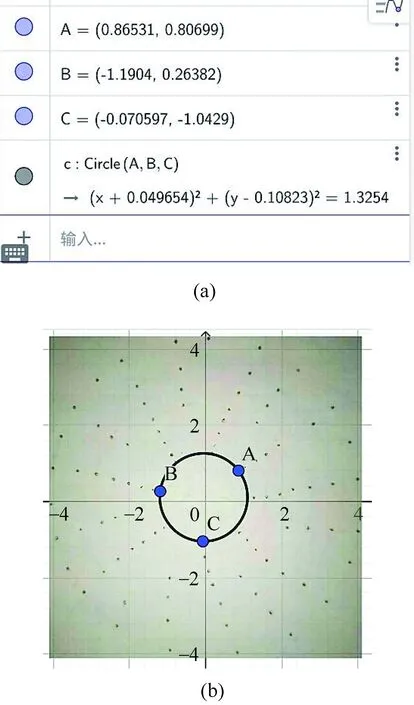
图6 最内侧等势点的拟合结果(a) 点的坐标及圆的方程式; (b)拟合出的等势线
对外侧等势点重复上述两个步骤。最终得到一系列的等势圆及其方程。利用“向量”工具可垂直于等势线绘制出电场线,如图7所示。
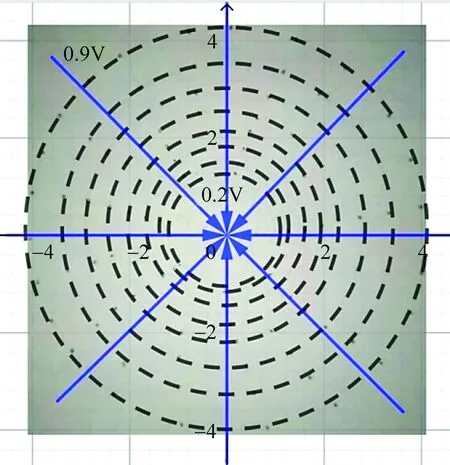
图7 等势线及电场线模拟图

图8 三维等势圆柱面模拟图(a) 正视图; (b)斜视图; (c) 剖面图
利用“3D绘图区”模块中的“圆柱”功能,按照所得圆的方程建立三维立体等势圆柱面图。在此基础上,用手指触屏拖动三维图形即可实现三维等势面的平移或旋转,图8(a)、(b)、(c)分别为模拟出的三维等势面的正视图、斜视图及剖面图。通过上述操作学生可在各自的智能手机上进行立体圆柱等势面的多角度观察。
3.2.3 对数拟合
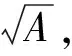
选中B、C两列,进行“双变量回归分析”,选择“对数”作为回归模型进行拟合,则省去了计算半径对数值的步骤,可直接得到U与r的拟合曲线及其方程,即图9(b)中的y=0.13284+0.54068lnx,则U与lnr线性关系的斜率k值为0.54068。
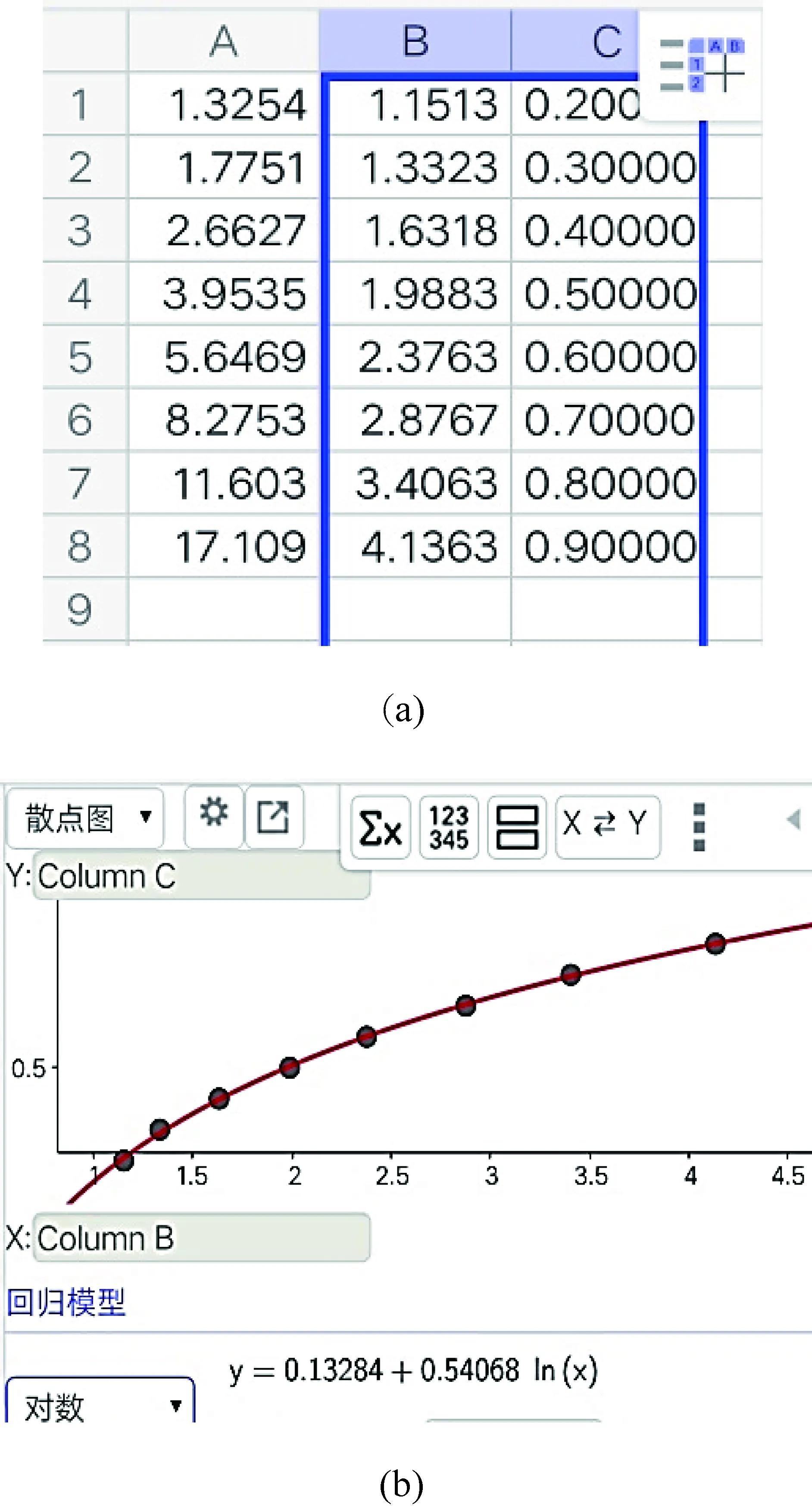
图9 手机软件的拟合结果(a) 数据表格; (b)对数拟合曲线及方程式
根据式(3),可计算得斜率k的理论值。拟合结果相比人工计算拟合的结果更为准确,二者与理论值的比较如表2所示,基于智能手机的拟合结果准确率提高了2.0%。

表2 两种方法结果与理论值的比较
3.3 基于手机软件进行数据处理的优势
基于智能手机中的相机及GGB软件进行静电场描绘实验的数据处理避免了手动处理时繁冗的数据测量、记录和计算过程, 也无需学生携带或使用计算机,仅需一部手机即可完成整个数据处理过程。处理过程方便、快捷,且计算精度较高,保证了实验的准确性。学生们也可在手机上观察到静电场的二维等势线及三维等势圆柱面,使得静电场描绘实验更加生动直观。
此外,此软件还可实现保存、导出图片、分享等功能,学生们可以随时保存数据处理结果,也可以利用智能手机中的多种社交软件将文件传输给同学或老师进行文件共享或作业的提交等工作,在一定程度上实现了物理实验的智能化和信息化,实现了疫情期间对物理实验的的线上居家学习。同时,在新工科的建设背景下,将智能手机应用于传统的物理实验过程中可在一定程度实现“厚基础”的升级创新。
4 结语
本研究将静电场描绘实验与智能手机相结合,使传统的静电场实验实现了智能化计算模拟。改进后的静电场模拟描迹实验的处理方法避免了手动描线、计算半径平均值、线性拟合等大量的数据处理过程,大大减少了计算量,节省了实验时间,且保证了计算的精确度。本方法普适性强,能够使学生们有效利用手中的智能手机,准确且高效地完成数据处理过程,并直观观察到二维等势线与三维等势面,使传统的静电场实验变得简易、生动且直观,对实验教学老师开拓思路也有参考意义。

