面向应用型本科的“离散数学”教学改革研究

都娥娥，圣文顺

（南京工业大学浦江学院，江苏南京 211200）

0 引言

“离散数学”（又称计算机数学）是现代数学的重要分支，是计算机科学理论的基础，作为应用型本科计算机相关专业的核心基础课程之一的“离散数学”正变得日益重要。它是以研究离散量的结构和相互之间的关系为主要目标［1］，在计算机理论研究及软、硬件开发的各个领域都有着广泛的应用。“离散数学”也是计算机科学中的数据结构、操作系统、编译原理、数据库系统原理、算法分析、逻辑设计、系统结构、容错技术、人工智能等许多课程的先导课程［2］。

对于面向应用型本科的高校而言，在学生的培养上，立足于培养信息技术与应用实践相结合的特色型社会人才，注重能力与素质并重，满足社会各界对高质量应用型人才的需求。但是通过实际的教学实践及效果来看，发现在教学中存在一些问题，与学校定位的培养方向产生部分背离，尤其是一些理论性很强的学科，比如“离散数学”，在学习过程中，知识点抽象，学生感觉理解较为困难，进而缺乏兴趣。

本文将以“离散数学”中的部分内容为例，从教学内容、教学方法、实践设计等方面进行探讨，将教学内容与实际应用相结合，使用相关知识点来解决日常生活中的问题，引导学生加强知识点的理解，提高学习兴趣。

1 “离散数学”教学中存在的问题

1.1 教学模式的限制

在正常的教学中，“离散数学”一般的教学时长都是48～64课时，但是其涵盖面较广，正常都包含数理逻辑、集合论、图论、代数结构几大模块，有的教材还增加有组合数学和形式语言与自动机等的相关知识，因此这门课的典型特点就是概念/定理多、内容琐碎、知识点抽象。就以“图论”的相关知识来说，作为“离散数学”课程中的重要知识模块之一，内容十分丰富，在整个“离散数学”中所占比重最大（如图1所示）。随着计算机科学的迅速发展，图论在许多学科的应用也相当广泛，诸如运筹学、信息论、控制论、计算机科学等，都是以图作为工具来解决实际问题和理论问题［3］，因此，学好图论知识并能灵活运用就显得至关重要。

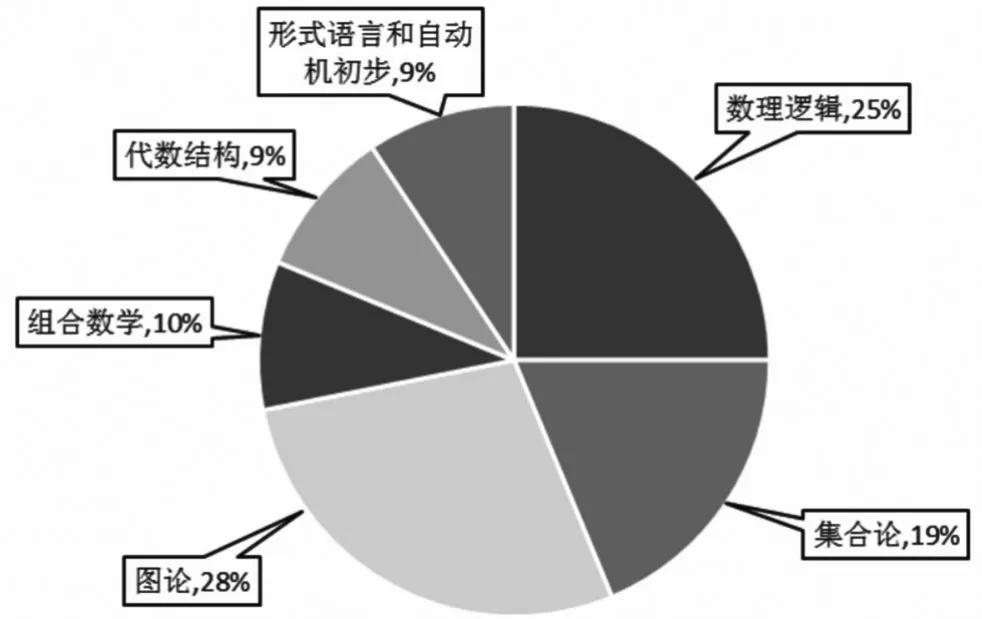
图1 “离散数学”各知识模块课时比例

目前，在“离散数学”这门课程的授课中，大部分教学均采用传统的授课模式进行教学，即按照数学的教学方式进行讲解，把一个个概念、定理和证明非常生硬地讲给学生，这对学生来说听起来觉得枯燥无味，理解上难度大，学起来不明白它到底在计算机科学和实际的生活中有什么用处。例如，在教学中占据比重最大的“图论”内容［4］，图的分类较多，各个图的概念定理都较为抽象，不同的图有不同的判断定理，有的使用充分必要条件判断，而有的只能使用必要条件的逆否命题判断，有的又要使用充分条件来判定，判定方法多而抽象。在这种情况下，由于知识点多，迫于进度，教师只能按照课本进行定义和定理的讲解和证明，这种典型的照本宣科的教学方式，授课速度太快，学生无法跟上老师的教学思路，更加大了学生对知识点的理解难度，使其教学效果大打折扣。

1.2 教学缺乏实践设计

对于应用型本科而言，学生大多时候关注的是如何将学到的知识进行应用，如何提高自己的动手能力，才能在毕业找工作时对自己有所帮助。而传统的“离散数学”教学设计上只有理论教学，无实践环节，由于不需要做上机实验，因而经过一段时间的学习，学生发现自己除了知道一些知识点和概念外，所学的知识在实际生活中并没有得到应用，而且也不知道如何使用这些知识，进而在真正遇到需要用“离散数学”的知识点来解决实际问题的时候，不能活学活用，在解决问题能力上也比较欠缺，同时对后续专业课程的学习也不能起到良好的铺垫作用。

像“离散数学”这种典型的纯理论、缺乏实践、考研又不是必考科目的课程，只能使学生的学习停留在枯燥的理论层面，对未来要从事信息化建设类工作的学生来说，无法将所学的知识与计算机软件设计、编程等相关能力结合起来［5］，总觉得不如去写段代码、组件一个计算机网络来的实用。这门课程也常常因为这些情况，无法让学生产生学习兴趣而去主动地进行学习，长此以往，就会形成学“离散数学”没什么用，只求考试通过的学习风气，进而渐渐地不被同学重视。

针对上述问题，本文从教学内容、教学方法、实践环节等几个方面做了教学改革的尝试和研究。

2 “离散数学”教学改革研究

2.1 教学内容的删减

由于“离散数学”内容较多，就如目前我们专业选择的教材除了传统的几大知识模块外，还增加了“组合数学”和“形式语言与自动机”等方面的内容，所以在实际授课时候，可以根据实际需要进行相关内容的删减。如“形式语言与自动机”的相关知识目前对于学生用处不是很大，可以不列入教学计划，“组合数学”相关内容因为在计算机编码、算法设计及密码学方面有较大的用处，可以列入教学计划进行讲授。而且需要根据各个知识模块在实际应用中所占的比重，加大比重较大的知识点的课时数，如“图论”部分。对于集合部分，因为学生以前或多或少接触过相关知识，所以在授课时候，集合的基本概念和运算方面可以加快点进度，在关系、函数的复合及反函数等章节可以多举例子进行讲解，加深理解。

2.2 教学方法的改进

“离散数学”这门课传统的教学方法较为古板，教师大部分照本宣科，无法引起学生的学习兴趣。因此，如何在教学方法上进行相应改进，提起学生对这门课的兴趣显得至关重要，提起学习兴趣后再进行知识点的讲解，这样所取得的效果会好很多。本文以“图论”部分的内容为例来从以下两个方面探讨教学方法的改进。

2.2.1 趣味入题

在进行新的知识点讲授的时候，尽量以一些有趣的话题来引入所讲的内容，首先引起学生的注意，让学生不再感觉到这门课是枯燥乏味的，调动其积极性。

例如，在讲“图论”知识的时候，可以先向学生讲述图论的起源：18世纪中叶在欧洲普鲁士的哥尼斯堡城内有一条河，河中有两个小岛，由七座桥相连接。当时人们热衷于一个难题：一个人怎样不重复地走完这七座桥？这就是著名的哥尼斯堡七桥问题。当时很长时间没人能解决这一问题，直到1736年，欧拉发表了第一篇关于图论的论文，将该题转化为图论问题才得以解决［3］。以这样的趣味性问题入题，进而引申出相关的知识点，能够使学生对这些内容留下深刻的印象，也可以提起对后面知识的学习兴趣。

2.2.2 结合实际讲授知识点

在授课过程中，为了加深学生对抽象的知识点的理解，尽量将该知识点和实际中的例子结合起来，让同学了解到在遇到不同的问题时使用哪些知识点来解决。

例如，在讲“图论”中的哈密顿图［6］时候，由于哈密顿图的特殊性，至今没有一个较好的定理或者方法来判定，都是结合各种必要条件、充分条件进行判断。定理多，每种判断方法都存在局限性，使学生无法理解哈密顿图到底有何使用。这时候可以列举一个现实生活中的例子，来加深学生的理解和了解哈密顿图的用法。如：某次国际会议8人参加，已知每人至少与其余7人中的4人有共同语言，问服务员能否将他们安排在同一张圆桌就座，使得每个人都能与两边的人交谈？这个例子就可以使用到哈密顿的知识点来解答，可以将参加与会的人员看成图的8个顶点，如果两个人有共同语言，就给他们之间画一条边进行关联，进而转化为图论问题。由于每个人都可以和其他7个人中的4个人有共同语言，所以每个顶点的度数至少为4，根据判断哈密顿图的充分条件知道，两个顶点的度数之和大于实际顶点数，则是哈密顿图［3］，所以该题肯定存在一条哈密顿回路，服务员只需要在该图中找一条哈密顿回路，然后按回路中相邻关系安排座位即可解决此题。

上述例子在现实生活中是极可能存在的推理问题，对这类题感兴趣的同学肯定很多，这时借助所学知识就能很简单地解决实际中的复杂问题，以这样的方式进行内容讲解，既不会让学生感觉到枯燥乏味，还能引起学生的兴趣，提高同学解决实际问题的能力。

2.3 增加实践环节

前面阐述了对于应用型本科生而言，最主要的是实际动手能力，而要提高动手能力，实践环节必不可少。但是传统的“离散数学”课程无实践环节，只说离散数字在计算机中应用广泛，学生无法理解如何使用“离散数学”的知识去解决与计算机相关的问题。为了解决这一问题，本文提出在正常的教学中，增加一些实践内容，加深学生对知识点的理解和巩固，同时也可以提高学生的动手能力。

例如，在讲“图论”中的最短路径问题时，使用到了著名的算法——Dijkstra算法，教材上已经给出了该算法的具体步骤。在教学中，可以将该算法列入实践内容，让学生用自己熟悉的语言，编写出该算法的相应代码，给定一个特定的图，规定起点和终点，调用自己编写的算法函数，求出最短路径。然后用数学上的方法，手动绘制该图的最短路径计算过程图表，最后也会确定一条路径，去验证是否和程序运行的结果一致。

通过对类似的内容增加实践环节，不但加深学生对知识点的理解，而且使学生的编程能力得到了锻炼，也使学生对自己产生很大的自信，能运用已经学过的编程语言和“离散数学”的知识，编写出小的应用程序，解决一些算法问题，进而对学习也产生浓厚的兴趣。

3 结语

“离散数学”作为计算机科学技术的支撑学科之一，正变得日益重要，在计算机的各个领域都有重要的应用，同时它又可以提高学生的思维能力，使其在解决计算机问题时候激发一些设计思想。通过对“离散数学”课程进行一系列的教学改革实践后，上述教学改革措施非常有效，大大提高了学生的学习兴趣，将理论与实践相结合，加深了学生对知识点的掌握，也提高了学生的实际动手能力，取得了较好的教学效果。