基于常规测井资料计算煤层力学参数
陈东锐,王延斌,韩文龙,王 力
(1.中国矿业大学(北京)地球科学与测绘工程学院,北京 100083;2.中联煤层气有限责任公司晋城分公司,山西 晋城 048000)
煤储层岩石力学参数(泊松比、弹性模量等)是应力场模拟、储层压裂改造设计的基础参数[1]。横波资料也是各类工程参数准确计算的基础[2]。对于纵波和横波速度的重建,前人做了很多研究。李敬功在Xu-White模型的基础上,建立了以空间模量差值比为基础的横波时差拟合模型[3]。马中高将Gardner公式进行了推广,建立了密度与纵、横波速度的关系式[4]。上述一系列研究成果多集中在常规砂泥岩地层,针对煤储层的横波时差构建方法尚不多见。本文在已有的针对砂泥岩地层的横波速度估算方法的基础上,构建适合于煤岩层段的横波时差计算方法,搭建起岩石力学参数计算的桥梁,能够在计算得出研究区煤储层各项岩石力学参数基础上,揭示纵向上连续的煤储层力学性质参数及其变化特征,为煤储层集中射孔压裂施工提供基础数据。
1 研究区块概况
本次研究的柿庄北区块位于沁水盆地南缘沁水复向斜东翼东部缓坡带,目标煤层3号煤层位于山西组底部,埋深800~1000m,发育稳定,平均厚度5.45 m,储层压力梯度介于0.61~0.859MPa/100m,煤层储层温度介于27.5~30.27℃,平均孔隙度为5.63%,渗透率为0.085×10-3μm2左右,平均含气量17.11 m3/t,本区块煤层气拥有较好的开发潜力[5]。
2 构建横波时差拟合模型
对于密度与纵、横波速度的关系,不同研究者针对不同岩性的岩石,提出了不同的经验公式。但是岩石本身比较复杂,而且不同区域变化不一,煤层的地质特征与砂泥岩地层有很大的不同。为探索研究区煤岩层段纵、横波时差及密度测井之间内在相关性,选取本区已经进行过多极阵列声波测井的井作为标准井,提取其煤岩层段纵、横波时差和密度测井数据,分别构建了横波时差与纵波时差、横波时差与密度测井数据的交会图(见图1、图2)。
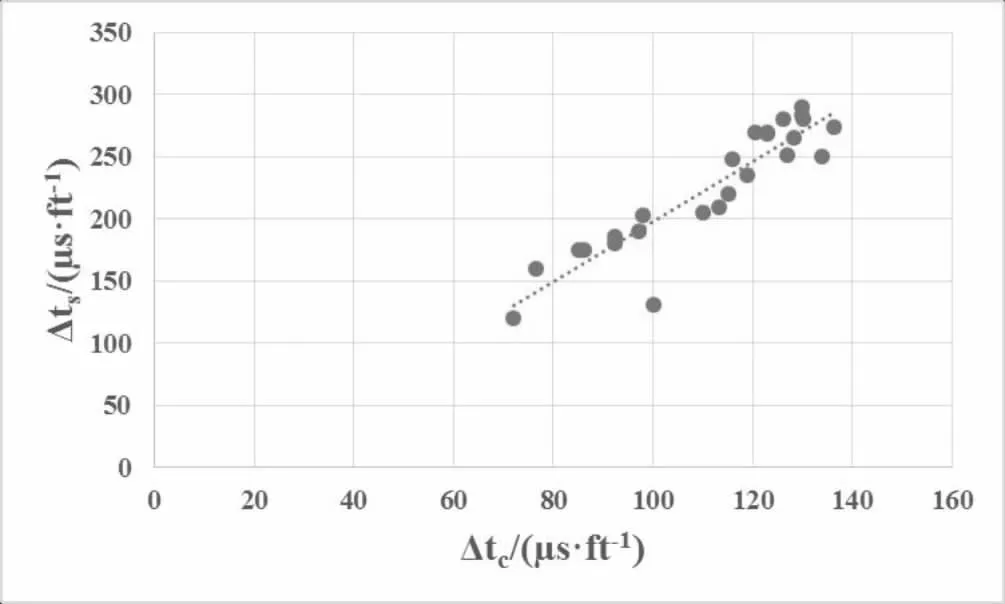
图1 纵波时差-横波时差交会图

图2 密度-横波时差交会图
从图1、图2中看出,煤岩层段的横波时差与纵波时差、横波时差与密度测井相互之间具有较好的线性相关性。拟采用纵波时差、密度测井为参数对横波时差进行拟合,并建立多元拟合模型。
Gardner(1974)[6]提出了对各种岩石平均的纵波速度与密度(ρ)的函数形式 ρ=AVpB。因此,对于煤岩层段的横波时差与纵波时差、密度测井采用多元非线性模型来进行拟合,得出方程(1),R2=0.91。

利用建立的多元非线性模型方程(1)进行计算得出的横波时差与实际测量值相比结果如图3所示,其相对误差介于0.12~10.17,平均相对误差为5.14。
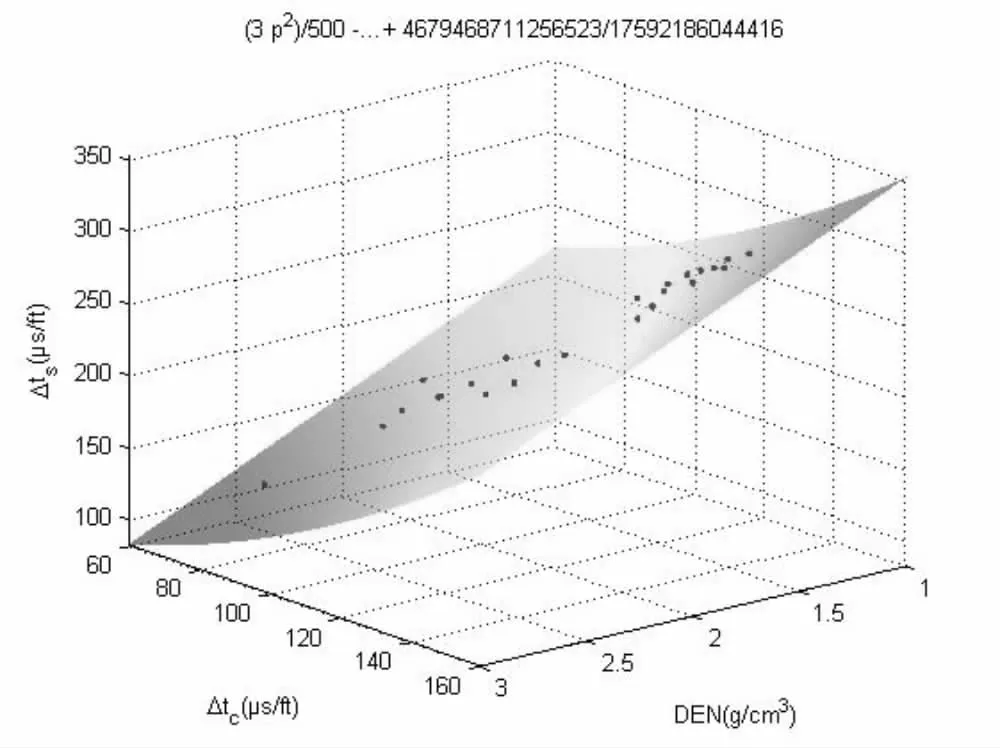
图3 密度和横、纵时差拟合模型结果与实测数据比较
3 煤层力学参数计算与分析
通过岩石力学试验只能获得单个层位岩石力学参数,而利用测井资料可以获得连续的岩石力学参数,并且能够显示纵向上力学性质的连续变化特征。岩石形变主要力学参数包括泊松比、剪切模量以及弹性模量等[7],上述各种力学参数可由纵波时差Δtp、横波时差 Δts和岩石密度ρ计算求得。
选取研究区某井主力煤层3#煤层井段进行分析研究。某井3#煤层埋深1497.00~1502.80m,平均纵波时差为131.7μs/ft,平均横波时差为211.7μs/ft,平均纵横波速度比为 1.61,平均密度值为1.30g/cm3。提取本井3#煤层段的纵波时差与密度测井响应值代入方程(1)进行计算,可以得出其剪切模量在2.21~4.77GPa范围变化,平均值为2.87GPa;泊松比值在0.26~0.37范围变化,平均值为0.32;弹性模量在4.15~16.32GPa范围变化,平均值为7.64GPa。
本井段取煤样5块进行室内力学实验,试验采用RMT-150B岩石力学实验系统,得到实验结果如表1所示。可以看出,测井解释成果与室内实验获得力学参数基本一致。

表1 实验室力学参数实验结果
4 结论
1)运用纵波、密度测井与横波时差的关系构建拟合模型较为简单、便捷,免去了中间参数值的计算,避免了参数值计算不准确而引起的误差,且模型相关系数较高为0.91,计算结果精度也比较高。然而,对于不同煤层,不同的研究区域,拟合模型是否能推广使用,还需要进一步分析与验证。
2)在煤层力学参数计算中,目标煤层剪切模量在2.2~4.4GPa范围变化,泊松比值在0.07~0.26范围变化,弹性模量在4.15~16.32GPa范围变化,计算所得力学参数与实验室测试结果基本一致,计算得出的纵向上连续的力学参数也能够为后期施工提供数据基础。

