周向波纹圆柱壳屈曲特性研究

徐 戎，张 山，李胜秋

（1.招商局重工（江苏）有限公司，江苏 南通 226116；2.江苏科技大学机械工程学院，江苏 镇江 212003）

潜水器是深海探测重要科学工具，耐压壳是潜水器的关键部件，其质量占潜水器总质量的1/4～1/2［1］，它能承受海水的巨大压力，为工作人员提供安全的工作环境，使设备正常工作。柱形壳是一种常用的耐压结构，其特点是空间利用率高、流体运动阻力小、制造方便。但是这些圆柱壳在承受外压时容易发生屈曲，往往导致无法恢复的坍塌。

一般来说，存在许多提高圆柱壳屈曲能力的方法。首先，改变子午线形状是一种有效的方法。例如，Blachut和其同事研究发现等质量的桶形壳具有比未加筋圆柱壳更高的屈曲能力［2-3］。最近，张建等人，研究了卵形壳及其在海洋工程中的应用［4］，发现长卵形压力壳对屈曲行为具有有效的抵抗。另一种方法是添加加强筋或波纹来提高圆柱壳的屈曲能力［5］。在这些加强方法中，波纹加强是最优的选择，其不需要额外的加强筋就能够提高柱形壳的屈曲能力。Ross等［6］对周向波纹圆柱形耐压壳的非线性屈曲进行了理论、数值和试验研究，Ghazijahani等［5］采用试验法研究了波纹个数对周向波纹圆柱壳屈曲特性的影响。但是，上述研究都是基于相同幅值的波纹柱壳，对不同幅值的波纹柱壳研究较少。

因此，本文讨论了在均布外压下波纹圆柱壳的屈曲特性。设计了1个普通圆柱形耐压壳和2个周向正弦波纹柱形耐压壳，并且采用数值分析的方法研究线性屈曲、非线性屈曲以及波纹幅值对柱壳的影响规律。

1 周向波纹柱壳几何模型

波纹柱形耐压壳模型的结构示意图如图1所示。波纹柱形耐压壳的具体几何参数列于表1中，波纹柱壳的几何参数：模型的直径D＝160 mm，高度H＝230 mm，壁厚t＝2 mm，正弦波纹均匀的分布在柱形耐压壳上，波纹的幅值s＝0 mm，2.5 mm，5 mm，当波纹柱形耐压壳的幅值s＝0mm时，此柱壳为普通柱壳，波纹的跨距S＝20 mm，金属密封盖厚度T＝10 mm。

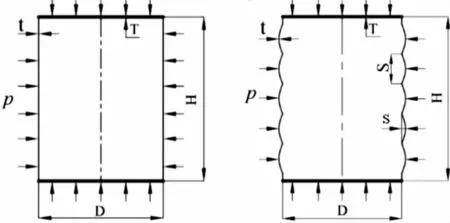
图1 柱壳模型几何外轮廓Figure 1 geometric outline of cylindrical shell model

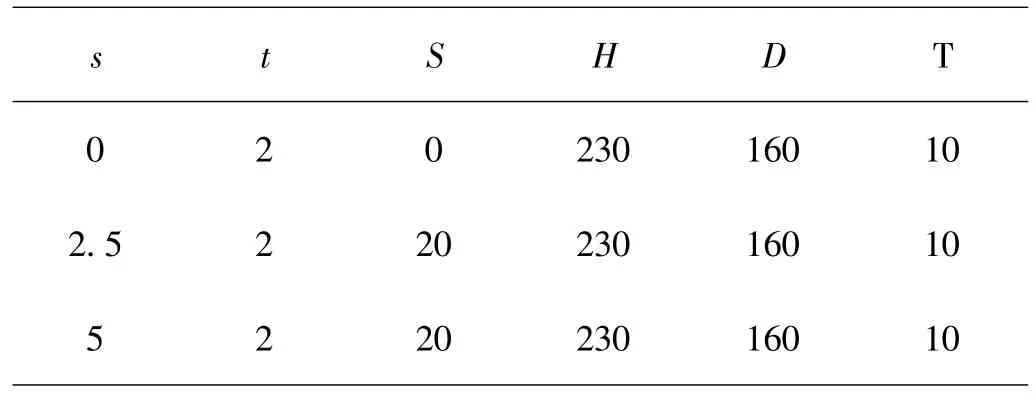
表1 柱壳的几何参数Table 1 geometric parameters of cylindrical shell mm

2 有限元分析

2.1 数值模型

本章选用ABAQUS/Standard对柱壳进行屈曲分析。它可以分析简单的线性分析，也可以进行大型的、复杂的非线性分析。首先，一般使用Solidworks软件对普通耐压壳和周向正弦波纹柱形耐压壳进行三维建模，把建好的模型保存为相应格式，接着把模型导入ANSA软件中、对柱壳划分网格，先要对模型进行TOPO操作，即对导入的模型缝合；因为柱壳的主体壁厚与其密封盖的厚度不同，所以在划分网格后要对其设置不同的PID，这样方便在ABAQUS中设置模型的几何参数。如图2所示，柱壳的两端的网格要呈钱币形状，即柱壳两端要使用钱币形的网格划分方式，这样才能更好的保证数值计算的准确性。

图2 柱形耐压壳的数值模型Figure 2 numerical model of cylindrical pressure shell

有限元模型利用全集成壳单元S4来避免沙漏。由于本文研究的柱形耐压壳是薄壳，故单元属性选择为壳单元。柱形耐压壳都赋予相同的材料参数，在圆柱壳的外表面施加单位均布压力 ，这里 P＝1MPa。图2是有限元模型的边界约束条件。由CCS2018［7］可知，工作时的柱形耐压壳不受约束。当对其进行整体计算时，耐压壳体需要3个支撑点，约束壳体在6个方向上的位移分量，边界条件需要对称设置：U x＝U z＝0，U y＝U z＝0，U x＝U z＝0，以上设置不仅可以消除耐压壳体的整体刚体位移，又不妨碍壳体的相对变形。

其中，波纹柱形耐压壳主体的材料参数为［8］：弹性模量E＝2122.92MPa，泊松比μ＝0.3284，抗拉强度为33.8～40.2MPa。此仿真即分析了波纹幅值对柱形耐压壳屈曲的影响，又分析了普通柱形耐压壳与波纹柱形耐压壳的屈曲性能。

2.2 数值计算结果分析

1）理想壳体的屈曲分析。本节有限元模型分析步设置如下：选用ABAQUS对波纹柱形耐压壳展开线弹性分析，选择Step中的Linear perturbation选项，然后在选项列表中设置Buckle作为线弹性分析步，并且设置特征模态阶数为6阶。ABAQUS提供了两种方法来提取特征值：Lanczos算法和Subspace iteration算法。这两种算法的使用范围不一样，当需要求解的特征模态阶数较高时一般推荐使用Lanczos算法；如果仅仅求解少量的特征模态（少于20阶特征模态）时，则使用Subspace iteration算法的速度可能更快。在此项分析中，将使用Subspace iteration算法，并计算出有限元模型的前6阶特征值与屈曲模态。

柱壳的线性分析结果如图3和表2所示。图3呈现出1个普通柱壳与2个正弦波纹柱壳的屈曲模式，三个柱壳均在其中间位置发生失稳；当波纹幅值s＝0mm，2.5mm，5mm时，它们的失稳波数分别为：5个、4个、3个。

图3 理想柱壳屈曲模式Figure 3 buckling mode of ideal cylindrical shell

从表2中发现，波纹柱形耐压壳的线性屈曲压力随着波纹幅值增大明显提高。这种增强可以归因于这样的事实，即与普通耐压壳的无限子午半径相比，波纹柱形耐压壳的局部子午半径显著减小了。结果表明，从平板到曲面，壳体的子午曲率越高，其承载能力越高。此外，屈曲波的减小可能是由于波纹柱形耐压壳的极高刚度导致的。

表2 理想柱壳线性屈曲载荷（Plb）Table 2 linear buckling load of ideal cylindrical shell（Plb）

由表2中看出，随着波纹幅值的增加，柱壳的线弹性屈曲载荷由100.06kPa增加到211.25kPa，表明在均布外压作用下，周向波纹柱壳线弹性屈曲的抗压性能优于普通柱壳。

2）真实壳体的屈曲分析。为了检验理想壳体屈曲失稳模式是否正确，要建立真实壳体的屈曲分析。首先，根据表1中的几何参数制作实物模型，每种模型制作2个，共计6个。然后对已经制作好的实物模型进行3D外轮廓扫描，将扫描完成的外轮廓保存为相应的格式，导入ANSA中进行网格划分，如图4所示，为普通柱壳扫描完成后的视图。

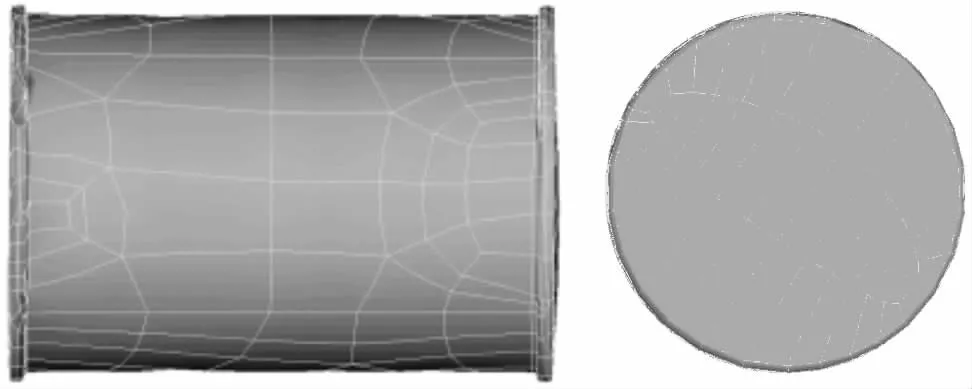
图4 三维轮廓扫描试验Figure 4 three dimensional contour scanning test

选用ABAQUS中的Static，Riks分析步对柱壳进行非线性分析，非线性屈曲值用Pnlb表示。由于扫描完成的模型中已经包含了初始几何缺陷，所以对真实壳体进行屈曲分析更能反映实况下壳体的失稳模式。

图5是真实柱壳的后屈曲模式，表3呈现了真实柱壳的线性屈曲载荷。

图5 真实柱壳的后屈曲模式Figure 5 post buckling mode of real cylindrical shell

表3 真实柱壳的非线性屈曲载荷（Pnlb）Table 3 nonlinear buckling load of real cylindrical shell（Pnlb）

由表3可知，相同波纹幅值柱壳的非线性屈曲载荷基本一致，表明实物模型制作精度较高；并且随波纹幅值的增大，非线性屈曲载荷也逐渐增大，这与理想柱壳线性屈曲载荷有相同的规律，而且线性载荷值与非线性载荷值高度吻合，说明线性屈曲分析的可靠性。

图5是真实柱壳的后屈曲模式，相同波纹幅值柱壳的后屈曲模式吻合度较高；并且图5的后屈曲模式与图3线性屈曲模式一致，失稳位置都是在柱壳的中间位置，这是典型的失稳模式。

3 结论

1）设计了一种周向波纹圆柱壳，随着波纹幅值增大，波纹柱壳抗屈曲的能力也随之增大，并且屈曲载荷增幅很明显，当波纹幅值s＝5 mm时，其线性载荷与非线性载荷均为普通柱壳（s＝0 mm）的2倍多。2）理想柱壳线性屈曲载荷值与真实柱壳非线性屈曲载荷值高度一致，说明了线性屈曲分析的可靠性，并且柱壳线性失稳模式与非线性失稳模式吻合良好。