弱幻方的代数系统

刘兴祥，刘娟娟，张 婧

(延安大学 数学与计算机科学学院，陕西 延安 716000)

幻阵学对研究代数的前沿问题有很大价值和影响，其中幻阵学的分支——弱幻方的定义及其代数系统前人还没有研究过。本文在幻阵学及抽象代数[1-7]的基础上，提出弱幻方的代数系统，对于丰富幻阵学与代数的研究内容，完善幻阵学与代数的框架体系具有重要意义。

1 弱幻方的相关定义

定义1 设F是数域，如果矩阵A=(aij)n×n满足

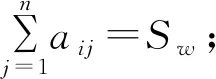
则称矩阵A称为数域F上的n阶弱和幻方，并称Sw为数域F上n阶弱和幻方A的弱幻和。

定义2 设F是数域，如果矩阵A=(aij)n×n∈Fn×n满足

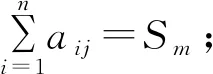
则称矩阵A称为数域F上的n阶和幻方，并称Sm为数域F上n阶和幻方A的幻和。

定义3 设F是数域，如果矩阵A=(aij)n×n∈Fn×n满足

则称矩阵A称为数域F上的n阶弱积幻方，并称pw为数域F上n阶弱积幻方A的弱幻积。

定义4 设F是数域，如果矩阵A=(aij)n×n∈Fn×n满足

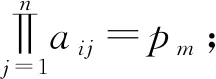
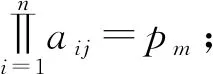
则称矩阵A称为数域F上的n阶积幻方，并称pm为数域F上n阶积幻方A的幻积。

定义5 设F是数域，如果矩阵A=(aij)n×n∈Fn×n满足

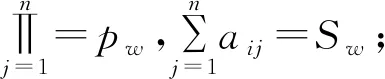
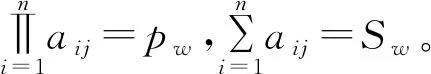
则称矩阵A称为数域F上的n阶弱和弱积幻方，并称pw为数域F上n阶弱和弱积幻方的弱幻积，Sw为数域F上n阶弱和弱积幻方的弱幻和。

定义6 设F是数域，如果矩阵A=(aij)n×n∈Fn×n满足

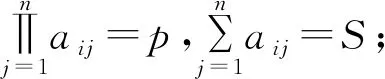
则称矩阵A称为数域F上的n阶和积幻方，并称p为数域F上n阶和积幻方的幻积，S为数域F上n阶和积幻方的幻和。

2 弱幻方的代数系统研究

定理1 设(S,+)是一个代数系统(半群、交换半群、群、交换群)，Mn(S)={A|A∈Sn×n，A是n阶弱和幻方}，对于Mn(S)中的矩阵定义如下二元运算⊕：∀A,B∈Mn(S),A⊕B=(aij+bij)n×n，则(Mn(S),⊕)是一个代数系统(半群、交换半群、群、交换群)。

证明对∀A=(aij)n×n∈Mn(S),

∀B=(bij)n×n∈Mn(S),∀C=(cij)n×n∈Mn(S)，

A⊕B=(aij+bij)n×n∈Mn(S)且

故所给二元运算⊕在Mn(S)上满足封闭性。

(A⊕B)⊕C=(aij+bij)n×n⊕(cij)n×n=

(aij+bij+cij)n×n=(aij)n×n⊕(bij+cij)n×n=

A⊕(B⊕C)，

故所给二元运算⊕在Mn(S)上满足结合律，因此Mn(S)是半群。

∀A∈Mn(S)，

因此O是Mn(S)中非零元A的单位元。

∀A∈Mn(S)，

-A⊕A=(-aij)n×n⊕(aij)n×n=

(-aij+aij)n×n=(0)n×n=O，

因此-A是Mn(S)中非零元A的逆元，因次(Mn(S),⊕)是群。

又因为矩阵加法对于交换律成立，即(Mn(S),⊕)是交换群。

(S,+)是一个代数系统，则(Mn(S),⊕)是一个代数系统证明完毕，其他证明同理可证。

推论1 设(S,+)是一个代数系统(半群、交换半群、群、交换群)，Mn(S)={A|A∈Sn×n，A是n阶和幻方}，对于Mn(S)中的矩阵定义如下二元运算⊕：∀A,B∈Mn(S),A⊕B=(aij)n×n⊕(bij)n×n=(aij+bij)n×n，则(Mn(S),⊕)是一个代数系统(半群、交换半群、群、交换群)。

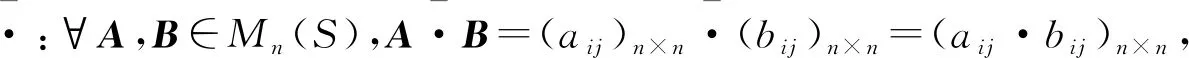
银行需加大产品租借的宣传和销售力度，提升市场营销人员的素质和专业知识，根据不同客户群的金融需求和银行自身实际情况来确定产品的不同组合，从而有效提高整体的营销和销售效果[8]。其次，应更深层次地进行产品多样化和专业化，促进交叉销售。一方面，城市商业银行要根据金融资源优劣势来对已有的金融服务和业务的功能和品种进行整合和完善；另一方面，要加强产品创新，为客户提供具有银行自身特色的个性化服务。

证明对∀A=(aij)n×n∈Mn(S),

∀B=(bij)n×n∈Mn(S),∀C=(cij)n×n∈Mn(S)，

∀A∈Mn(S)，

因此E是Mn(S)中非零元A的单位元即幺元。

∀A,B∈Mn(S)，

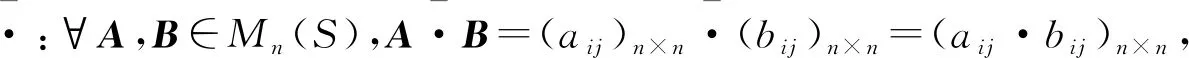
证明对∀A=(aij)n×n∈Mn(S),

∀B=(bij)n×n∈Mn(S),

∀C=(cij)n×n∈Mn(S)，

A⊕B=(aij+bij)n×n∈Mn(S)且

故所给二元运算⊕在Mn(S)上满足封闭性。

(A⊕B)⊕C=(aij+bij)n×n⊕(cij)n×n=

(aij+bij+cij)n×n=(aij)n×n⊕(bij+cij)n×n=

A⊕(B⊕C)，

∀A∈Mn(S)，

O⊕A=(0)n×n⊕(aij)n×n=(0+aij)n×n=A，

因此O是Mn(S)中非零元A的单位元。

∀A∈Mn(S),

-A⊕A=(-aij)n×n⊕(aij)n×n=

(-aij+aij)n×n=(0)n×n=O，

∀A∈Mn(S)，

因此E是Mn(S)中非零元A的单位元即幺元。

∀A,B∈Mn(S)，