基于形心轴的多轴增材制造工艺规划方法*

王炳杰，郝小忠，许 可，江 森

（南京航空航天大学机电学院，南京 210016）

新一代飞机的高性能指标使其设计上零件整体化、结构复杂化、尺寸大型化等特点日渐显著[1]，部分航空复杂零件需要高度定制化、小批量生产，对零件加工精度的要求越来越高，零件的价值也越来越大，也对制造方法提出了很大的挑战。增减材混合制造为航空复杂零件的加工提供了一种新的解决方案，通过将增材制造设备集成至多轴加工中心，实现了原位增材与减材一体化制造，融合了两种加工方式的工艺优势，可以实现航空复杂零件的高效率加工。

截至目前，已经有不少公司和机构成功研制出了混合制造设备[2-4]。然而，大部分混合制造应用中仍旧采用传统的三轴增材技术，不可避免地会在必要部位添加支撑结构。支撑结构的使用造成了材料的浪费，通过五轴切削加工去除支撑结构时，影响零件的整体加工效率，而且可能还会存在严重的刀具干涉问题，影响后续的增材制造工艺，使制造过程无法顺利进行。多轴增材制造通过引入更多的自由度，可以实现零件材料堆叠方向的适时调整，能有效地避免支撑结构的使用，因此更加适用于增减材混合制造。

增材制造逐层堆叠的工艺特性决定了其工艺规划中须对零件模型进行切片划分，而对模型切片结果的优劣直接影响其是否需要添加支撑结构，进而影响到后续工艺以及零件最终的成形质量。基于五轴加工中心的混合制造装备为多轴增材制造的实现奠定了硬件基础，然而，目前缺乏针对复杂零件的多轴增材制造工艺方法。因此，如何利用多轴增材制造的运动位姿空间实现无支撑增材制造，寻求一种行之有效的多轴增材制造工艺规划方法是亟待解决的问题。

增减材混合制造作为一种新兴的制造技术，逐渐成为研究和制造的热点技术，多轴增材制造作为其中的重要组成部分，国内外研究人员对其工艺规划已经进行了一定的研究。基于体积分解的多轴增材制造工艺规划方法是国内外学者研究最多的一类方法，根据他们提出的规则对模型进行体积分解，可以有效地避免支撑结构的使用，同时减少喷头与已成形零件的碰撞问题。Singh 等[5]沿定义的原始材料堆叠方向，通过基于轮廓边界的方法将零件分解成构建和非构建的子部件。对于非构建子部件，使用高斯和可视化重复映射方法确定一个新的构建方向，这种策略的应用复杂，而且对于具有内腔的复杂件计算量大。Dwivedi 等[6]提出了一种基于骨架线的多方向激光直接能量沉积工艺规划算法，通过对实体无支撑体积的识别以及对角取向的估计，可以在没有支撑的情况下制造出近净形零件。Ruan 等[7]提取模型的形心轴，通过分析形心轴的拓扑信息确定拆分面，以此进行分解并进行多轴分层，生成无碰撞分层序列。Ren 等[8]结合形心轴提取方法和基于模块化边界模型的分解方法，提出了一种自适应空间分解方法。

为了在通用模型上自动化生成高自由度增材制造的沉积路径，Wu 等[9]基于骨架线将模型分解为无需支撑的子部件，并确定所有部件的无碰撞材料堆叠方向。但该算法在处理其他模型时可能仍需添加支撑结构，并且为防止碰撞必须保证零件模型不是底面朝下。Wei等[10]最近开发了一种基于骨架线的体积分解算法，其目标是最小化体积分解总数和大小，分解的子部件可以实现无支撑增材制造。Ding 等[11]提出了一种基于简单曲率的分解重组方法，引入基于拓扑信息的深度树结构，将它们合并为有序的切片组。该策略在各种测试部件尤其是具有大量孔的零件模型上均有效，但该方法只能分解闭合的凹面环路区域，可能无法处理具有复杂几何形状的零件，也没有考虑碰撞等问题。

模型体积分解可以充分利用多轴增材制造多方向策略的能力，以上方法大多先对一些复杂的特征进行提取，这些特征一定程度上能够提供几何的整体视角，在最优序列的基础上进行体积分解操作。但以上特征提取算法的计算量通常比较大，而且大多只能处理一些简单形状的零件。

目前，多轴增材制造还没有得到很好的应用，仍缺乏有效的多轴增材制造工艺规划方法。这主要是因为多轴设备为增材过程提供了更多的自由度，使喷头与零件之间有了更多位姿控制的空间可能性，增加了多轴增材制造工艺规划求解空间，同时也给工艺规划带来求解难度。因此，本文提出一种基于形心轴的多轴增材制造工艺规划方法，通过检测切片层形心的改变来分解部件，使几何分析更加简单，保证零件的无支撑增材制造，并且计算速度较快。

1 形心轴的定义及提取

形心轴一定程度上能够表征零件模型的空间拓扑与形状信息，包括零件的空间延伸趋势。使用本文方法时，在增材制造过程中先沿着初始材料堆叠方向成形，垂直于提取到的形心轴方向进行切片，再根据自支撑临界角将零件模型分解，以分解位置形心轴方向作为新的材料堆叠方向，实现零件的无支撑增材制造。

考虑到对于复杂零件模型而言，难以直接求解其整体形心轴，需要按照一定的规则将零件模型进行分解，分别求出每一子部件的形心轴[12]。这里沿用“柱状”特征的定义[13]，即保证沿着当前材料堆叠方向切片时，零件模型与切片截面相交只能得到一个封闭轮廓。将零件模型按照“柱状”特征进行分解，保证每一个子部件都满足“柱状”特征的定义。

1.1 形心轴定义

给定“柱状”零件模型的一系列切片截面，求解切片截面与零件模型的相交轮廓，得到其离散点后可求出形心点Ci，依次连接所有轮廓的形心点，获得零件模型的形心轴。显然，该形心轴是一条折线，而形心轴实际上应是连续曲线，因此再对形心轴进行光顺处理，最终得到的形心轴如图1 所示（其中Ti表示形心点Ci–1处的切矢）。

图1 形心轴示意图Fig.1 Diagram of centroid axis

1.2 形心轴提取方法

提取零件模型的形心轴，需要先构造相应的切片截面。给定第i 个切片截面与零件模型的相交轮廓形心点Ci，以及对应的形心轴切矢Ti+1，可以通过式（1）求得第i+1 个切片截面上的近似点Si+1：

其中，δ 表示一定的计算步长，可以通过控制其大小来减小构造切片截面的误差。根据平面的点法式方程，给定平面上的一点以及该平面的法向量即可确定一个平面，将Ti+1作为第i+1 个切片截面的近似法矢Ni+1，然后求解第i+1 个切片截面与零件模型的相交轮廓，再计算得到其形心Ci+1，形心Ci+1处的切矢Ti+2可通过以式（2）近似求得，再计算其单位量。

增材制造中一般以STL 格式的文件存储零件模型，很容易得到零件模型的各种信息，包括模型的点、面以及它们之间的关系等，以此为基础设置边界条件。以零件模型的底面轮廓形心C0作为起始形心点，起始切矢定为T1=（0，0，1）；终止条件设置为判断第i+1 个切片截面与零件模型是否相交，若相交则继续上述算法，若不再相交则算法停止。

判断第i+1 个切片截面与零件模型是否相交，需要先提取相交轮廓；求解相交轮廓的形心，同样需要先对相交轮廓进行提取。求解相交轮廓就是切片截面与零件STL 模型三角面片求交的过程。2005 年Moller 等[14]提出一种算法，用于求解一条射线与一个三角形的相交点，在该算法基础上，本文提出以下相交轮廓的提取方法。

首先，给定第i 个切片截面的轮廓点Contour_pointi与第i+1 个切片截面的形心点Ci+1及形心轴切矢Ti+1，由Ci+1及Ti+1即可确定第i+1 个切片截面。通过相关数学公式可求出Contour_pointi在第i+1 切片截面上的投影点project_pointi+1，由project_pointi+1和Ci+1即可确定射线的方向：

进而确定一条射线：

一个三角形可以由3 个顶点V0、V1、V2确定，三角形上任意一点由以下公式确定：

其中，（u，v）是质心坐标，必须满足u ≥0，v ≥0 和u+v ≤1。计算射线R（t）和三角形T（u，v）相交，将两式联立：

调整后得到：

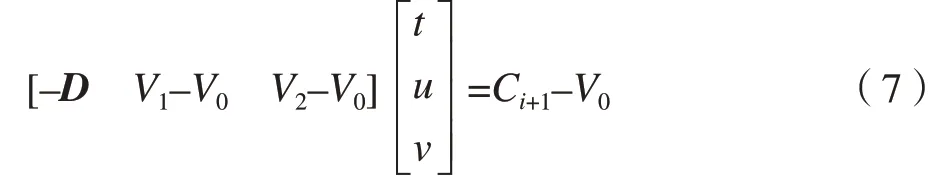
将E1=V1–V0，E2=V2–V0和T=Ci+1–V0代入，根据克拉默法则，式（7）等价于：

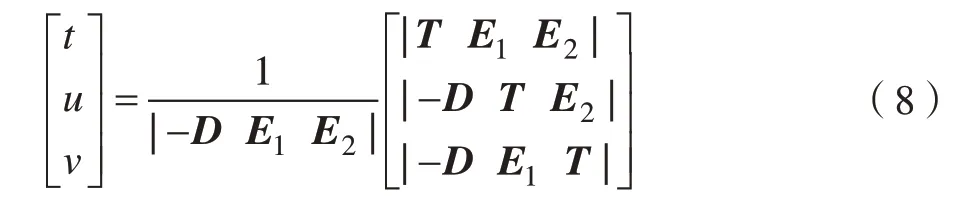
根据线性代数，知道|T E1E2|=–(T×E1)·E2=–(E2×E1)·T，式（8）等价于：

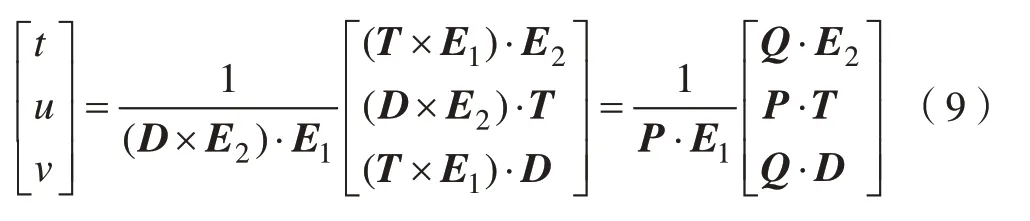
其中，P=D×E2，Q=T×E1。

经过上述计算过程即可得到t、u、v 的值，进而求得射线与三角面片的交点。使用相同的方法计算得到第i+1 个切片截面上的每个投影点与零件模型三角面片的交点，即为轮廓点Contour_pointi+1，将轮廓点首尾相连即可得到封闭的相交轮廓。

显然，通过上述方法提取的相交轮廓为空间不规则多边形,假设该多边形有n+1 个角点，其中第n+1 个角点（xn+1，yn+1）与第一个角点（x1，y1）重合。将这些角点投影到XOY 平面得到相应的投影角点Vi'，构成一个二维不规则多边形，可直接求解其形心Ci'的坐标

其中，A 为多边形的面积：

空间不规则多边形形心点Ci的x、y 坐标与其投影点相同，而其z 坐标zCi的求解只需将该坐标点（xCi，yCi，zCi）代入到已知的相应切片截面方程，从而求得Ci的坐标，形心轴提取过程如图2 所示。

2 基于形心轴的体积分解方法

2.1 分解约束条件的构建

在零件的增材制造过程中，为了避免支撑结构的使用，应保证每一切片层侧面的三角面片法矢ni与对应的材料堆叠方向Bi满足以下要求：

其中，α 为实现无支撑增材制造的自支撑临界角，不同的材料具有不同的α 值，需通过试验标定。如图3 所示，若ni与Bi的夹角小于α+90°，利用材料的自支撑性能可顺利成形；若ni与Bi的夹角大于α+90°，沿当前材料堆叠方向继续增材会导致材料掉落，从而难以成形。因此，α+90°为ni与Bi的最大允许夹角，本文以此构建体积分解的约束条件。

2.2 基于形心轴的体积分解算法

使用上述方法获取零件模型的形心轴，基于构建的分解约束条件对模型进行体积分解。初始化材料堆叠方向为B1=[0，0，1]，从零件模型底面开始，以一定步长δ沿形心轴方向Tj进行切片，获得轮廓点Contour_pointi，搜索不满足约束条件式（12）的切片位置，在该位置将零件模型进行分解，并将该处形心轴切矢方向作为新的材料堆叠方向，将分解子部件存入到SubcomList 中，然后继续搜索，直至无法获得轮廓点。

图2 形心轴提取过程示意图Fig.2 Diagram of centroid axis extraction process

图3 分解约束条件示意图Fig.3 Diagram of decomposition constraint

基于形心轴的体积分解算法具体如下：

3 试验验证

本文所提出的算法已在MATLAB 中实现，并且为验证本文方法的可行性，设计了代表性模型示例。本文通过熔融沉积成型（FDM）增材制造工艺方式，使用PLA 材料进行试验验证，经过试验标定其自支撑临界角α 为45°。

本文设计的试验零件模型如图4 所示，其中蓝色区域表示使用传统的三轴增材制造时需要在该区域添加支撑结构，并使用Meshmixer 软件生成了支撑结构。

图5（a）所示为使用本文方法提取的形心轴，垂直于该形心轴方向进行切片。在切片的过程中，依据本文提出的基于形心轴的体积分解算法，搜索不满足约束条件式（12）的切片位置，在该位置将零件模型进行分解。其中初始材料堆叠方向为竖直向上，分解后材料堆叠方向调整为分解位置的形心轴切矢方向，然后继续搜索，直至零件模型分解完成。使用本文方法分解结果如图5（b）所示，该零件模型被分解为4 个部分。

由于试验条件所限，使用传统的三轴FDM 增材设备分别成形各个子部件用以表征在五轴FDM 设备上的3+2 多方向成形过程，这些组件都可以实现无支撑增材制造，试验验证过程中设置的相关参数如表1 所示，实际制造结果如图6 所示。

图4 试验零件模型Fig.4 Experimental part model

图5 试验结果Fig.5 Experimental results

表1 试验验证相关参数Table 1 Related parameters of experimental verification

图6 实际制造结果Fig.6 Actual manufacturing results

4 结论

多轴增材制造理论上可实现零件的无支撑增材制造，然而多轴姿态的引入增加了工艺规划求解空间，极大提升了工艺求解难度。体积分解是最常用的多轴增材制造工艺规划方法，但其特征提取算法计算量通常比较大，而且大多只能处理一些简单形状的零件。本文使用的形心轴提取算法计算效率高，基于此提出的体积分解算法也实现了零件的无支撑增材制造，并通过试验验证了本文方法的可行性。

目前试验验证中使用了分块增材制造的方式，后续会使用多轴增材设备进行一次性整体制造。多轴联动增材设备能实现材料堆叠方向的适时调整，能更有效地避免支撑结构的使用，未来将在此基础上进行更多关于多轴增材制造工艺规划的研究。