铁路隧道限界检测曲线地段数据折减计算与原理
陈诗韵
(南宁局集团公司 工电检测所,工程师,广西 南宁 530001)
铁路隧道限界检测对于超限货物的运输以及铁路设备的运营安全意义重大,大修施工导致隧道限界发生变化时,必须立即进行限界检测,确保铁路运输安全。隧道限界检测数据的处理过程中,曲线上的数据折减是较为复杂的一个部分,有的工作人员在实际应用中因对计算方法原理不甚理解、盲目套用公式而导致计算错误的情况时有发生,为避免此类问题,本文将详细介绍铁路隧道曲线地段限界检测数据折减的计算方法及基本原理。
1 曲线地段数据折减计算方法
根据《铁路建筑实际限界测量和数据格式》(TB/T3308-2013)的规定,以大地为基准的曲线地段测量数据,按“1.1”的要求进行高度换算,再按“1.2”的要求进行折减;以钢轨为基准面的曲线地段测量数据,按“1.3”的要求进行数据折减,测量数据以毫米为单位,并向下取整。上述两种情况具体计算简述如下:
1.1 以大地为测量基准建筑限界高度换算以大地为测量基准,即测量仪器位于线路中心且调节测量仪器水平时,曲线内侧建筑限界高度按公式(1)进行换算,曲线外侧建筑限界高度按公式(2)进行换算。

式中:
B——实测建筑限界半宽,单位为:mm;
H——计算点自轨面算起的高度,单位为:mm;
H0——实测建筑限界高度,单位为:mm;
θ=arctan(h/1500);
h——外轨超高值,单位为:mm。
1.2 以大地为测量基准建筑限界折减计算以大地为测量基准,即测量仪器位于线路中心且调节测量仪器水平时,曲线内侧建筑限界折减按公式(3)计算,曲线外侧建筑限界折减按公式(4)计算。

式中:
X——折减后的建筑限界半宽,单位为:mm;
R——曲线半径,单位为米(m)。
1.3 以轨面为测量基准建筑限界折减计算以轨面为测量基准时,曲线内侧建筑限界折减按公式(5)计算,曲线外侧建筑限界折减按公式(6)计算。

2 计算原理分析
2.1 以大地为测量基准的建筑限界高度换算铁路建筑实际限界测量主要采用限界检测车、限界测量仪作为测量工具,其中限界检测车的检测效率比普通的限界测量仪高得多,因而作为主要的测量工具用于铁路建筑实际限界测量。限界检测车的整个测量过程是在铁路线路上运行的过程中完成的,因此其测量数据是以轨面为测量基准。以大地为测量基准的建筑限界高度换算指的是采用普通的限界测量仪进行测量时,测量仪器位于线路中心线上并调节水平的情况下对实测高度进行的换算。以轨面为测量基准时,实际测量高度为垂直于线路中心线的平面内测量建筑物和设备内轮廓点(最近点或最高点或最低点)距两轨顶连线的垂直高度H,以大地为测量基准时,实际测量高度为垂直于线路中心线的平面内测量建筑物和设备内轮廓点(最近点或最高点或最低点)距两轨顶连线中点处所在水平线的垂直高度H0,高度换算即是将H0 换算为H。建筑限界高度示意见图1。
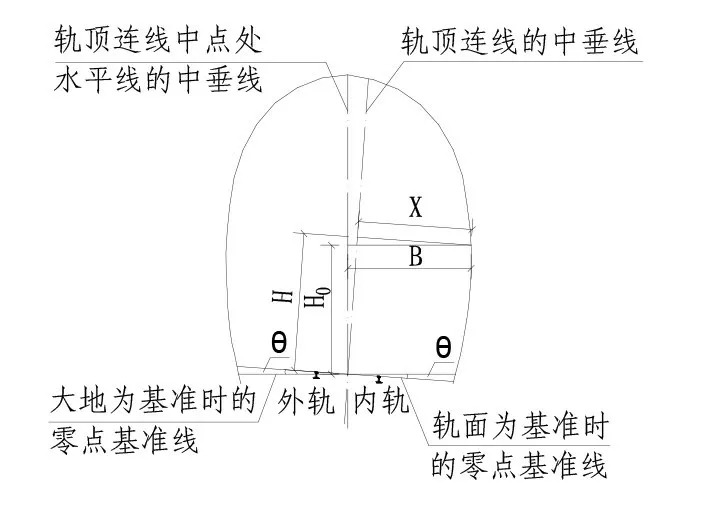
图1 建筑限界高度示意
由图1 可知,以轨面为测量基准时,实测高度等同于以大地为测量基准时,内股钢轨一侧以轨顶连线中心作为基准,向下旋转了θ 角(θ=arctan(h/1500)),即零点基准高度变低,从而导致内侧实测高度变大(较以大地为基准面时);外股钢轨一侧以轨顶连线中心作为基准,向上旋转了θ角(θ=arctan(h/1500)),即零点基准高度变高,从而导致外侧实测高度变小(较以大地为基准面时)。从图1 中还可看出,以轨面为基准时,实测半宽X已经包含了因外轨超高引起的曲线建筑限界折减值,无须再做相应的折减。
建筑限界高度换算示意如图2所示。
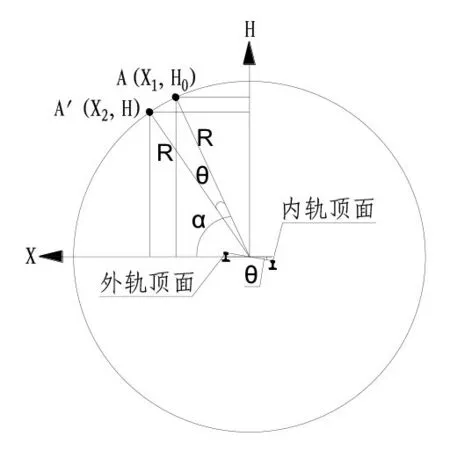
图2 建筑限界高度换算示意
由图2 可知,曲线外侧A 点(X1,H0)纵坐标H0是以大地为测量基准的实测高度,将其向下旋转θ角至A'点(X2,H)的纵坐标H 是以轨面为测量基准的换算高度。公式2(曲线外侧建筑限界高度换算公式)推导过程如下:
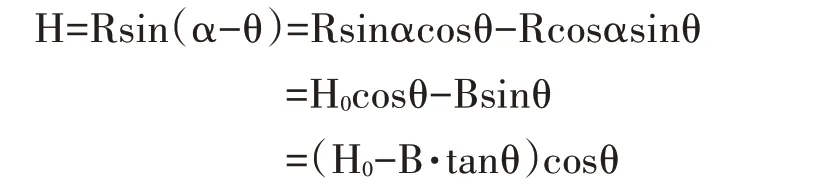
同理可得公式1(曲线内侧建筑限界高度换算公式)。
2.2 不考虑外轨超高曲线建筑限界折减计算由于列车在曲线上运行时,车辆轴线与线路中心线有偏距,导致车辆中部存在偏向曲线内侧超限,车辆两端存在偏向曲线外侧超限,因此对于实测曲线上隧道建筑限界,需要进行曲线建筑限界折减。图3 为曲线建筑限界折减示意图。图3中de为列车在曲线上运行时车辆中部轴线偏向线路内侧的偏距,ac(a'c')为车辆两端轴线偏向线路外侧的偏距,计算出de、ac(a'c')即可求出列车在曲线上运行时的曲线建筑限界折减值(不考虑外轨超高)。

图3 曲线建筑限界折减示意
1)曲线内侧建筑限界折减值(不考虑外轨超高)计算原理。
如图3 所示,de 即为曲线内侧建筑限界折减值(不考虑外轨超高),根据三角形相似原理,de×(2Rde)=l2/4,由于铁路圆曲线半径通常为几百乃至上千米,而de 通常只有几厘米,故de 近似等于l2/(4×2R)=l2/8R,规范在计算中采用的车辆最大长度L 为26 米,车辆前后转向架间距l 取18 m,将l 值代入公式计算得de=40500/R(mm),即列车在曲线上运行时的曲线内侧建筑限界折减值(不考虑外轨超高)为40500/R(mm)。
2)曲线外侧建筑限界折减值(不考虑外轨超高)计算原理。
如图3 所示,ac(a'c')即为曲线外侧建筑限界折减值(不考虑外轨超高),ac=bd=be-de,2.1.1 中已求得de=l2/8R,同理可求得be 近似等于L2/8R,ac=bd=be-de=L2/8R-l2/8R,将L、l 值代入公式计算得ac=84500/R-40500/R=44000/R(mm),即列车在曲线上运行时的曲线外侧建筑限界折减值(不考虑外轨超高)为44000/R(mm)。
2.3 由外轨超高引起的曲线建筑限界折减计算
由于曲线线路上存在外轨超高,车辆通过时会引起车辆对垂直位置的倾斜,因此对于实测曲线隧道建筑限界,需要进行建筑限界折减。外轨超高引起的曲线建筑限界折减目前共有2种计算方法:《铁路建筑实际限界测量和数据格式》(TB/T3308-2013)中外轨超高引起的曲线建筑限界折减值按H×h/1500计算(下称普通计算法);《铁路技术管理规程(普速铁路部分)》(铁总科技2014[172]号)中补充了外轨超高引起的曲线建筑限界折减的另外一种计算方法旋转限界法。外轨超高引起的曲线建筑限界折减曲线外侧为负,内侧为正,即曲线内侧做正折减,折减后实测限界值变小,曲线外侧做负折减,折减后实测限界值变大。
2.3.1 普通计算法计算原理 普通计算法的基本原理是用图1(建筑限界高度示意)中的高度H 乘以θ角的正切值(即h/1500)近似代替实测建筑限界半宽(B)与折减后的建筑限界半宽(X)的差值。
2.3.2 旋转限界法计算原理 旋转限界法是指以曲线地段内侧轨顶为轴,将限界旋转θ角(θ=arctan(h/1500))后通过计算对应高度位置限界的水平偏移量作为超高引起的曲线建筑限界折减值,旋转限界示意见图4,图中同一高度处虚实线间的水平距离即为上述折减值。旋转限界法坐标计算示意见图5,以内侧轨顶作为坐标原点,建立如图5所示坐标系,实测限界A 点(x,y)绕内轨顶面旋转θ角(θ=arctan(h/1500))后移动至A'(x',y')点,A'(x',y')点水平坐标x'与y'高度对应的原限界水平坐标之差即为超高引起的建筑限界折减值。y 轴左侧限界逆时针转动后点的坐标按照公式(7)、(8)计算,y 轴右侧限界逆时针转动后点的坐标按照公式(9)、(10)计算。

图4 旋转限界示意
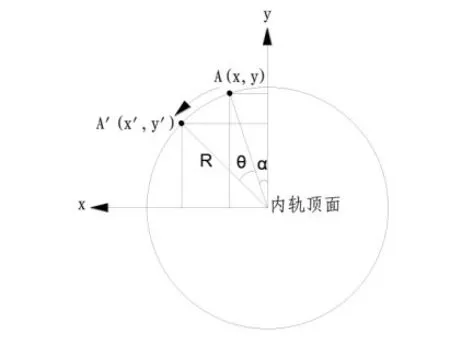
图5 旋转限界法坐标计算示意
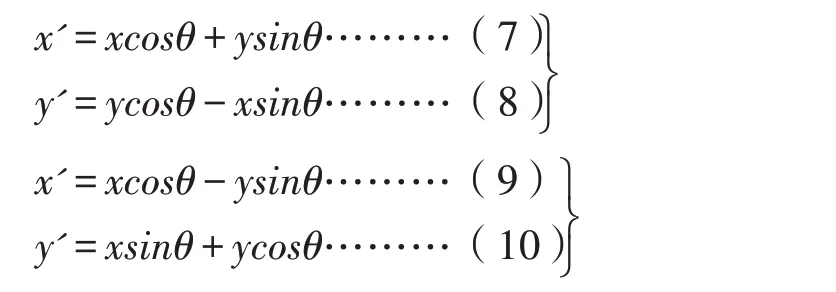
公式(7)、(8)推导过程:
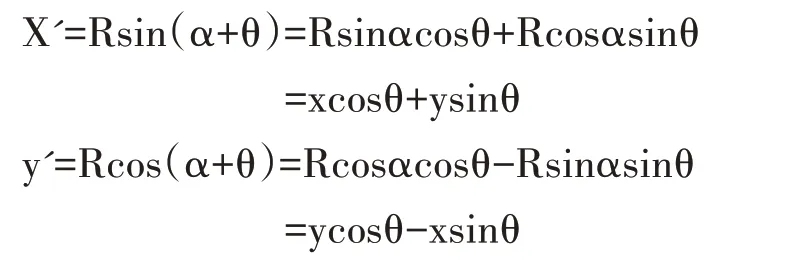
同理可推导公式(9)、(10)以及限界顺时针旋转情况下的计算公式,y 轴左侧限界顺时针转动后点的坐标按照公式(9)、(10)计算,y 轴右侧限界顺时针转动后点的坐标按照公式(7、(8)计算。
3 结束语
隧道内曲线地段限界检测数据的折减计算直接关系到限界检测数据反映限界实际情况的真实性和准确性,是铁路运输安全决策的重要依据,本文详细阐述了其计算方法及基本原理,以期为同类计算工作提供参考。

