基于ARIMA的入境旅游月度过夜人次预测

袁路妍 王占宏

摘 要： 入境旅游人次预测对旅游管理部门合理配置旅游资源、创新旅游服务模式有很重要的意义。受气候变化、经济发展趋势、文化差异的影响，旅游人次呈现出明显的季节性与非线性特征，管理部门依据经验推断入境旅游过夜人次的难度越来越大。文章采用ARIMA模型，对入境旅游过夜人次进行月度预测更加科学、准确。选取上海市2004-2016年入境旅游月度过夜人次数据为样本，依据AIC、BIC、HQIC最小准则进行参数估计和模型定阶，拟合出入境旅游月度过夜人次预测的最优模型为ARIMA（6，3，0）。运用该模型，对上海市2017年1-12月的入境旅游月度过夜人次进行预测，并将预测值与2017年真实数据比对，其平均绝对误差为3.22%。可见，应用ARIMA对入境旅游月度过夜人次预测有较高信度。

关键词： 入境旅游; 月度过夜人次; ARIMA; 非线性特征

中圖分类号： TP 391; F 590      文献标志码： A

Monthly Inbound Tourism Overnight Arrivals Forecast with ARIMA Model

YUAN Luyan， WANG Zhanhong

（1. College of Information Engineering， Shaoxing Vocational & Technical College， Shaoxing， Zhejiang 312000， China;

2. Shanghai Triman Information & Technology Co. Ltd.， Shanghai 200042， China）

Abstract：

Forecasting the number of overnight inbound tourists is of great significance for tourism management department to scientifically allocate relevant resources and innovate their service modes. Affected by climate change， economic development trend and social and cultural differences， the number of tourists has obvious seasonal and non-linear characteristics. Therefore， it is increasingly difficult for the management department to forecast the number of overnight inbound tourists based on experience. This paper uses the ARIMA model to make monthly forecast of the number of overnight inbound tourists， which makes the forecasted data more scientific and accurate. The paper， taking the inbound tourism data of Shanghai from 2004 to 2016 as samples， based on the minimum criteria AIC， BIC and HQIC， conducts parameter estimation and model ranking， ARIMA （6，3，0） is selected as the best model to forecast the monthly number of overnight inbound tourists in Shanghai. With the model， the monthly number of overnight inbound tourists in Shanghai from January to December 2017 is predicted. The mean absolute error between the predicted data and the real data in 2017 is 3.22%， which indicates that ARIMA is reliable in forecasting the number of monthly overnight inbound tourists.

Key words：

inbound tourism; monthly inbound arrivals for overnight stay; ARIMA; nonlinear characteristics

0 引言

入境旅游已然成为我国旅游业的重要组成部分，对入境旅游过夜人次预测，探测入境游客的出行特征，有助于旅游管理部门制定更加合理、有效的旅游规划。受季节变化、经济发展、文化差异的影响，入境旅游过夜人次的季节性、非线性特征十分明显，游客流量预测仍是当前研究的重点、难点。目前，针对旅游客流量预测方面主要采用ANN、SVR、ARIMA模型。ANN模型在非线性客流量预测方面表现出一定的优势，但易出现自身局部最优的问题，且要求训练样本足够大[1-2]。SVR为解决非线性、小样本客流量预测提供了一种有效的方法，但难以消除季节性影响。ARIMA模型利用差分方法消除季节性影响，可将多种因素综合效应融入时间序列变量中[3]，能够准确模拟和预测实际问题的动态变化情况，在实际应用中比较广泛。在入境旅游人次预测方面，邓祖涛等[4]于2006年利用BP神经网络对我国入境旅游人数做了年度预测;陈丽等[5]运用PCA-SOR-LS-SVM模型对来香港旅游的日本游客数量做了年度预测，虽然取得较好的预测效果，但选取的样本数据为1967～1996年日本游客到香港旅游的数据，若用于今天已经快速发展的我国中心城市旅游预测，其可用性不高。总之，除香港外，针对地方入境旅游人次预测研究，未见报道。上海、北京、广州等国家级的政治、经济、文化中心城市每年吸引了大量的外国游客，入境旅游人次比较大，其入境旅游人次受经济、文化、政策等外在因素的影响更大，非线性特征更加明显，故针对该类城市入境旅游人次预测的研究更具意义和挑战。为此，本文以上海市2004～2017年入境旅游数据为例，提出运用ARIMA模型对上海入境旅游月度过夜人次进行预测，并验证预测模型的可信度。

1 ARIMA模型

ARIMA模型全称为自回归积分滑动平均模（Autoregressive Integrated Moving Average Model，简记ARIMA），是一种重要的时间序列预测方法，由博克思（Box）和詹金斯（Jenkins）于70 年代初提出 [6-8]。ARIMA模型的一般表达，如式（1）所示。

式中p为自回归阶数， φ1，…，φp 为自回归系数，q为滑动阶数，θ1，…，θp 为滑动平均系数，{t，t-1，…，t-q }为随机序列或白噪声序列。ARIMA模型也经常表示为ARIMA（p，d ，q），d为差分次数。ARIMA模型实现时间序列预测的过程如下：

（1） 时间序列预处理

ARIMA模型能够实现对平稳的、非白噪声时间序列的趋势预测。因此在应用该模型前，需要对时间序列进行平稳性检验（ADF检验），若时间序列非平稳，经常采用差分方法进行平稳化处理，差分次数即为d的值。

（2） ARIMA模型识别

采用经

过d次差分后的平稳时间序列的自相关函数（ACF）ρk和偏自相关函数（PACF）φk进行模式识别。

计算式如式（2）所示。

若时间序列的自相关和偏自相关函数均是拖尾的，可以确定该时间序列的预测模型为ARMA（p，q），p和q的取值从低阶开始逐步试探，选择BIC值最小的 p，q值。

2 预测与评价

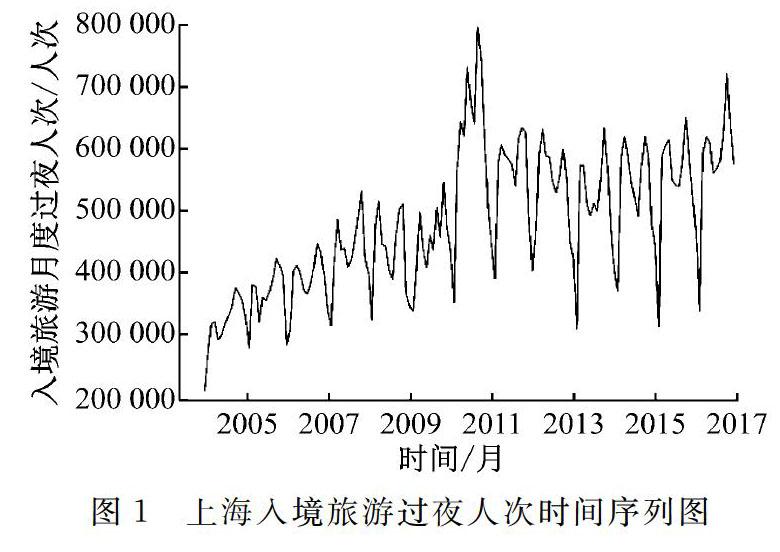
针对入境旅游月度过夜人次的预测，采用历年入境旅游过夜人次月度数据建立ARIMA模型做趋势外推预测。本文研究的样本数据为2004年1月至2017年12月的上海入境旅游过夜人次，其时间序列，如图1所示。

过夜人次预测实验环境为：一台PC机、windows10、pytharm-community-2017.2、Anaconda3、Python 3.6.6、statsmodels 0.6.1、matplotlib 2.0.0、numpy1.11.3、pandas0.19.2、prettytable0.7.2。实验选取2004～2016年的数据为训练集，拟合出最优预测模型，预测2017年各月入境旅游过夜人次。

2.1 时间序列预处理

（1） 奇异点识别和消除

由于干扰项的存在，时间序列中会出现一

些特殊的数据或数据段，他们的波动与数据集中其他的数据波动有着显著的不同，这种极少出现的数据点或者数据段成为奇异点[9]。本研究中，受2010年上海世博会影响，2010年的入境旅游过夜人次明显高于其他年份，认为该年度的数据段为时间序列中的奇异点。消除奇异点的方式采用前项数据与后项数据均值代替，调整后的时间序列图，如图2所示。

（2） 时间序列非平稳性处理

本研究对图2所示的非平稳时间序列进行3次差分，差分后的时间序列，如图3所示。

2.2 时间序列平稳性及非白噪声检验

通过statsmodels自带ADF检验库，实现对差分后的序列进行平稳性检验，即ADF单位根检验，检验结果如表1所示。

ADF检验值为-11.720 949，其值小于1%、5%、10%置信区间下的T统计量，证明差分后的序列是平稳的，并确定模型中d的值为3。延迟6阶的基于卡方分布的P统计量為4.792 671e-16<0.05，拒绝原假设，确认该序列不是白噪声序列。

2.3 模型识别和定阶

AIC准则即最小化信息量准则为模型选择提供了有效的规则，但其不足是拟合误差会受样本容量的放大，而参数个数的权重系数却和样本容量没有相关性。BIC准则即贝叶斯信息准则能够有效弥补AIC准则的不足，因此，在进行ARMA（p，q）参数的选择时，将AIC和BIC结合，依据AIC、BIC、HQIC最小准则寻找相对最优模型[10]。从低价开始计算ARMA模型的AIC、BIC、HQIC的值，计算结果如表2所示。

2.4 模型预测与评价

运用ARIMA（6，3，0），对2017年1～12月上海入境旅游月度过夜人次进行预测，其预测结果如表3所示。

可见预测趋势与真实趋势基本吻合，拟合效果较好。

3 总结

本文以上海入境旅游数据为例， 选取2004至2016年各月入境旅游过夜人次数据并拟合出最优模型ARIMA（6，3，0）。利用该模型预测2017年1～12月的入境旅游过夜人次与2017年真实数据比对，其平均绝对误差为3.22%，应用ARIMA（6，3，0）预测下一年月度入境旅游过夜人次有较高的可信度。在运用ARIMA建模分析时，需要事先消除时间序列中突发性影响因素，因此该模型的预测结果反映的是入境旅游月度过夜人次一般变化规律，遇到自然灾害等突发性事件时，需要增加修正项。

参考文献

[1]

陈荣，梁昌勇，梁焱，等.基于APSO-SVR的山岳风景区短期客流量预测[J].旅游学刊，2013，27（3）： 51.

[2] 陈荣，梁昌勇，葛立新.基于SEA的AGA-SVR节假日客流量预测方法研究[J].旅游学刊，2016，30（5）：13.

[3] 潘静，张颖，刘璐.基于ARIMA模型与GM （1， 1） 模型的居民消费价格指数预测对比分析[J].统计与决策，2017（20）：112.

[4] 邓祖涛，陆玉麒.基于BP 神经网络在我国入境旅游人数预测中的应用[J].旅游学刊，2006，20（4）：49-53.

[5] 陈丽，张朝元.基于PCA-SOR-LS-SVM模型的入境游客流量预测研究[J].科技通报，2014，30（3），95-99.

[6] 吴爱萍，陈银苹，张天哲，等.ARIMA模型在乙肝发病预测中的应用[J].中国现代医学杂志，2012，22（22）：79.

[7] SUN Z Q. Medical Statistics[M]. 2nd ed. Beijing： Peoples Medical Publishing House， 2006： 461-477.

[8] BOX GEP， JENKINS GM. Time series analysis： forecasting and control[J]. San Francisco： Holden Day， 1976： 181-218.

[9] 苏卫星，朱云龙，刘芳，等.时间序列异常点及突变点的检测算法[J].计算机研究与发展，2014，51（4）：782.

[10] 郭松，许锡文，尹晓星.基于ARMA模型的基坑沉降监测数据分析[J].地矿测绘，2017，33（1）：12.

（收稿日期： 2020.01.01）