基于区间潮流算法的低压配电网分散无功补偿优化方法

陈宏岩，唐治国，陈琦，王永旭，吴路明

（南京国电南自电网自动化有限公司，南京 211153）

0 引言

目前，我国城市和农村配电网发展不均衡，城市配电网多以中高压为主，中压配电网直接将电能输送至居民楼配电箱转换为低压0.4 kV居民用电，配电网备用容量充足、供电距离短、电压偏移小、电能质量高。而广大的农村低压配电网由于供电半径大、负荷较分散、配电线路长且线径小，线路上的电压损耗较大，经常出现线路末端电压过低的情况，严重时还会导致泵类负荷无法正常启动，影响农业用户的正常用电［1-2］。为了解决这个问题，通常需要对低压配电网的无功功率进行补偿，达到改善电压质量的目的。

国内外学者针对低压配电网无功补偿配置问题开展了一些研究。文献［3］介绍了低压配电网的各种无功补偿方式，并着重分析了低压配电线路基于“二分之三法则”进行无功补偿配置的应用效果。文献［4］提出了一种以配电网网损最小化为目标函数、以各节点电压上下限和无功补偿点补偿容量上下限为约束条件的低压配电网无功补偿分散配置优化模型。文献［5］提出了低压配电网分散无功补偿与扩大线径协调优化的计算模型，目标函数综合考虑了安装无功补偿装置和更换导线的投资成本以及降低配电网损耗的经济效益，约束条件包括配电网运行约束以及无功补偿点补偿容量和扩大线径支路截面积的上下限约束。文献［6］提出了考虑泵类负荷特性的低压配电网分散无功补偿优化配置模型，模型中目标函数综合考虑了补偿装置的投资成本和降低台区网损的经济效益，约束条件包括配电台区在泵类负荷正常运行和启动条件下的各种约束。上述文献针对低压配电线路无功补偿和低压配电网分散无功补偿提出了优化方案，但都是基于固定容量的无功补偿，没有考虑负荷变动不确定性较大的情况，这种情况下可能会出现无功功率过补偿的现象，影响配电网稳定运行。

本文提出了考虑负荷变动不确定性的分散无功补偿优化方法，根据低压配电台区各节点全年平均负荷，运用牛拉法计算节点电压偏移和无功功率缺额情况，根据给定的符合电压质量要求的节点电压区间，通过区间潮流算法和仿射运算得到无功功率补偿范围。通过对某个实际配电台区的计算分析，验证了该优化方法能够在负荷变动较大的情况下持续有效地改善台区电压质量，保证农业用户的正常用电。

1 基于牛拉法的区间潮流计算

1.1 牛拉法潮流计算模型

牛拉法潮流计算［7］分为直角坐标形式和极坐标形式，采用极坐标形式时，节点电压可以表示为

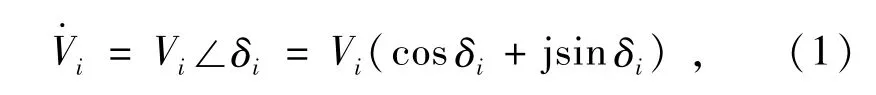
节点功率方程可以表示为

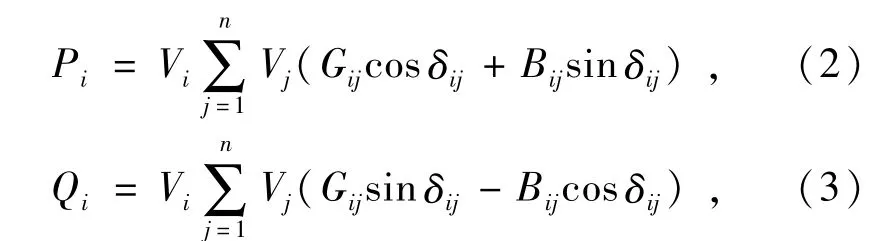
式中：Vi为节点i的电压幅值；δi为节点i的电压相角；Gij为节点i，j之间的电导；Bij为节点i，j之间的电纳；δij为节点i，j之间的电压相角差；Pi为节点i的有功功率输出；Qi为节点i的无功功率输出。

在n节点系统中，假设节点1—m是PQ节点，节点（m+1）—（n-1）是PV节点，节点n是平衡节点。Vn和δn给定，PV节点的电压幅值Vm+1—Vn-1也给定，因此只剩下m个节点的电压幅值V1—Vm和n-1个节点的电压相角δ1—δn-1是未知量。

对于每个PQ或PV节点，都可以列写一个有功功率的不平衡方程式

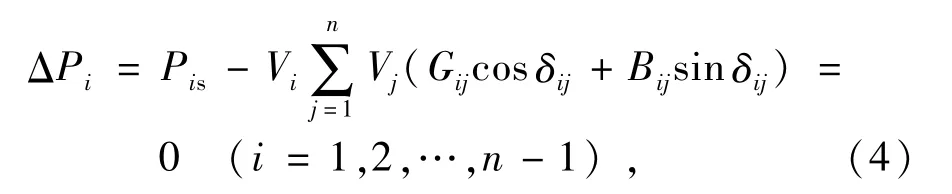
而对于每个PQ节点，还可以再列写一个无功功率的不平衡方程式

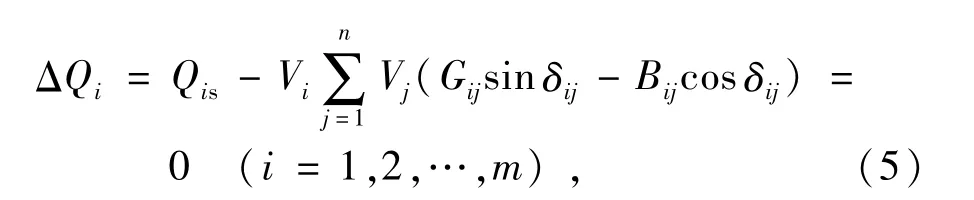
式中：Pis为节点i的有功功率输入；Qis为节点i的无功功率输入。

对于式（4）和式（5），可以写出修正方程式

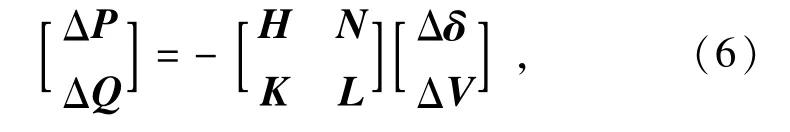
式中：ΔP为（n-1）×1阶方阵，其元素为节点有功功率修正量；ΔQ为m×1阶方阵，其元素为节点无功功率修正量；Δδ为（n-1）×1阶方阵，其元素为节点电压相角修正量；ΔV为m×1阶方阵，其元素为节点电压幅值修正量；H，N，K，L为雅克比矩阵的组成部分，分别为ΔP，ΔQ对Δδ，ΔV的偏导。

根据给定的初始值，进行迭代计算直至收敛，可以得到各节点电压的修正量，进而得到各节点电压的幅值及相角。

1.2 区间算法

对于一组给定的实数a-，a-∈R如果满足a-≤a-，则有界数集合

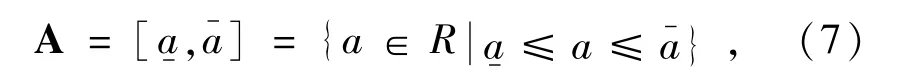
就叫做有界闭区间。其中a-为区间A的下端点，a-为区间A的上端点。

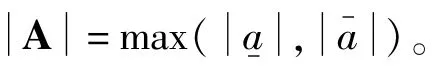
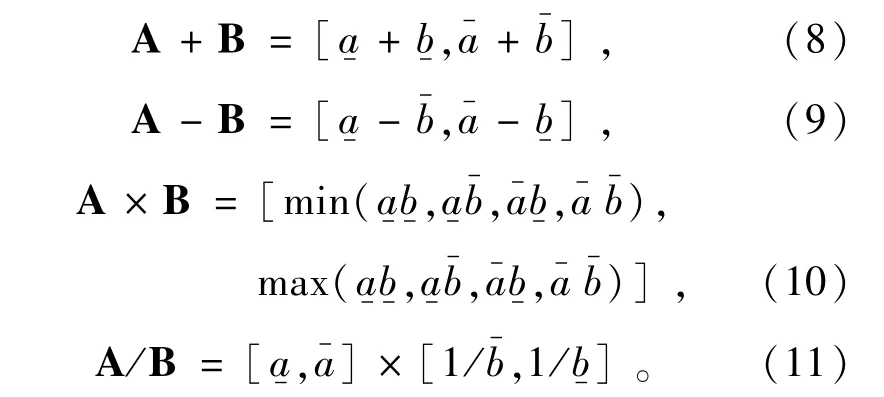
1.3 区间潮流模型

该系统的不平衡量方程式为

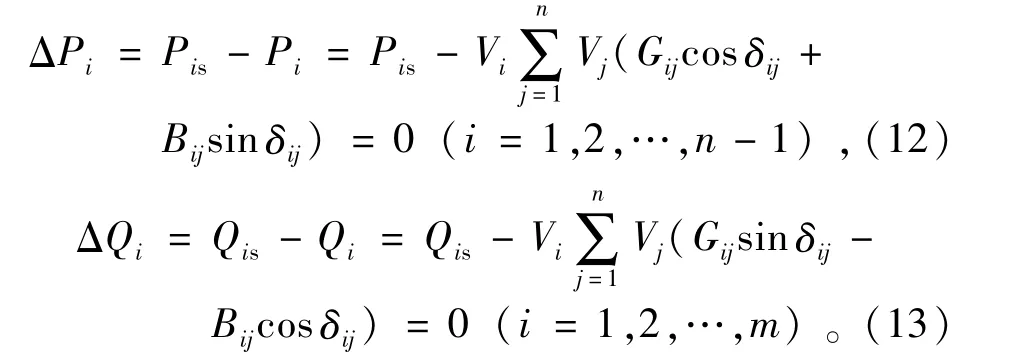
不平衡量方程组共有（n-1+m）阶，为了便于表述，可将其表示为

式中：h（x）为（n-1+m）个不平衡量方程式构成的函数。

首先需要求得迭代需要的K算子，初始区间给定为

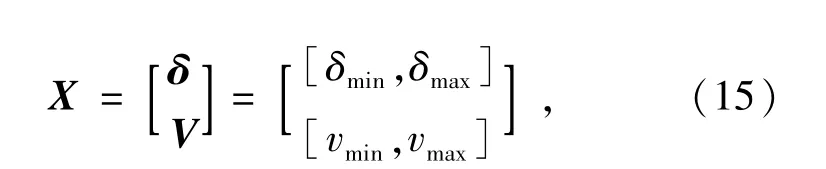
式中：δ为电压相角，是（n-1）维向量；V为电压幅值，是m维向量；下标min和max表示下限和上限。

取中点m（X）作为近似零点x*，则h（x）在中点的值为h（x*）。

对h（x）求偏导可以得到雅克比矩阵，该矩阵可以扩展为具有包含单调性的区间，即

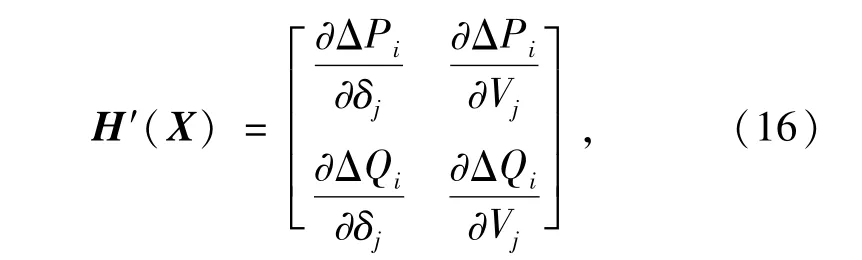
式中：H′（X）为h（x）对Δδ和ΔV求偏导得到的雅克比矩阵。

取T＝［m（H′（X））］-1，要求m（H′（X））必须是非奇异矩阵，否则就会引起T矩阵中的元素异常。为了防止m（H′（X））是奇异矩阵，在设置初始区间时应尽量使其不为对称区间。经过上述计算，可以得到K算子［8］

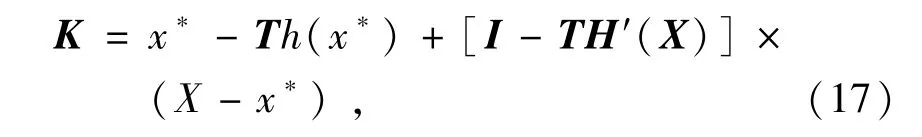
式中：I为单位矩阵。

利用K对区间X进行迭代

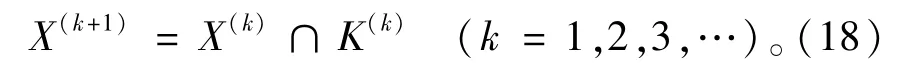
2 区间潮流算法改进

2.1 仿射算术

仿射算术［9］指出，各个不确定量之间存在一定的依赖关系，有了这个额外的信息，仿射算术的结果区间就可以收缩得更紧。给定一个仿射形式

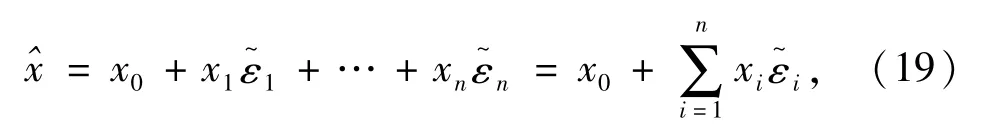
仿射算术与区间运算之间可以相互转换，例如上述仿射形式对应的区间可以写成

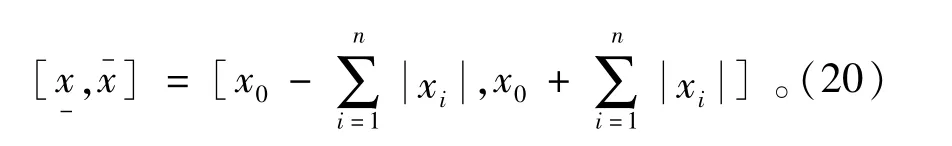
2.2 仿射运算对区间潮流的改进

仿射运算作为一种较为完善的算法，在很多领域得到了完美的应用。本文中只借鉴仿射运算中最基本的运算规则和相关性的思想，应用于区间潮流求解问题中。保留区间潮流算法的数学模型，只对K算子的组成元素做简单修改，使其在形式与运算法则上与原有的区间算法不同。

首先，将自变量写成二阶仿射形式

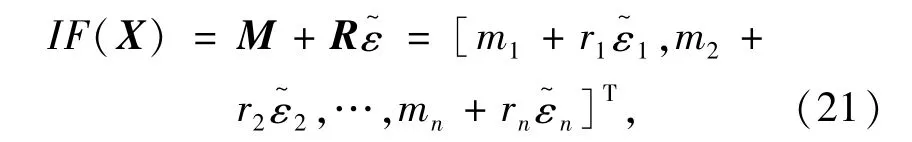
即

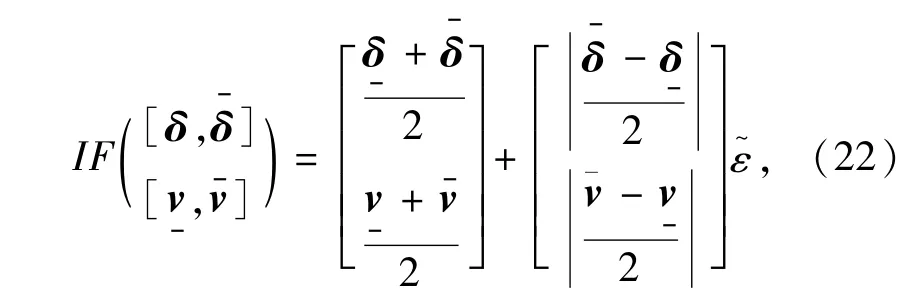
其中

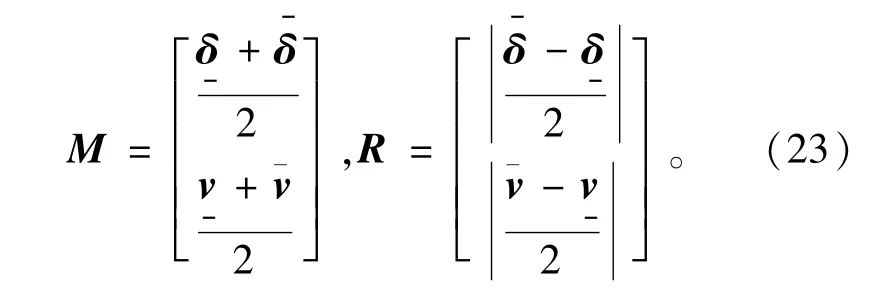
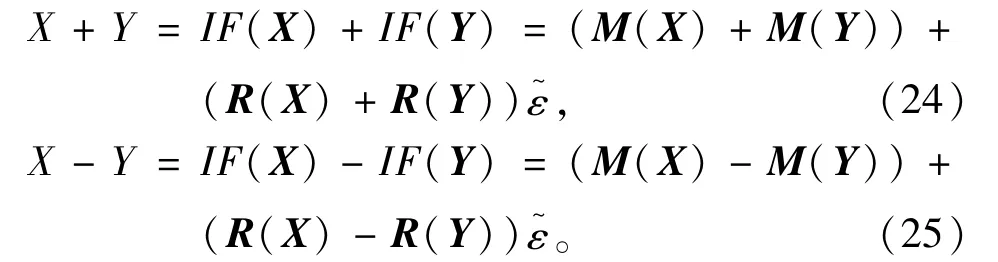
算子K ＝x*-T h（x*）+［I-TH′（X）］（Xx*）中，所有涉及加减法的元素均转换为仿射形式进行计算，乘除法保留区间算法的运算规则，最终得到的K算子用区间形式表示，与区间X取交集，再转换为二阶仿射形式进行下一次迭代。

3 算例分析

为了验证基于区间潮流算法的分散无功补偿优化方法的正确性及有效性，对某个实际低压配网台区进行计算，通过Matlab编程实现算法。

该台区为0.4 kV低压配电网，共有16个节点和15条支路，变压器高压侧额定电压为10 kV，低压侧额定电压为380V，如图1所示。

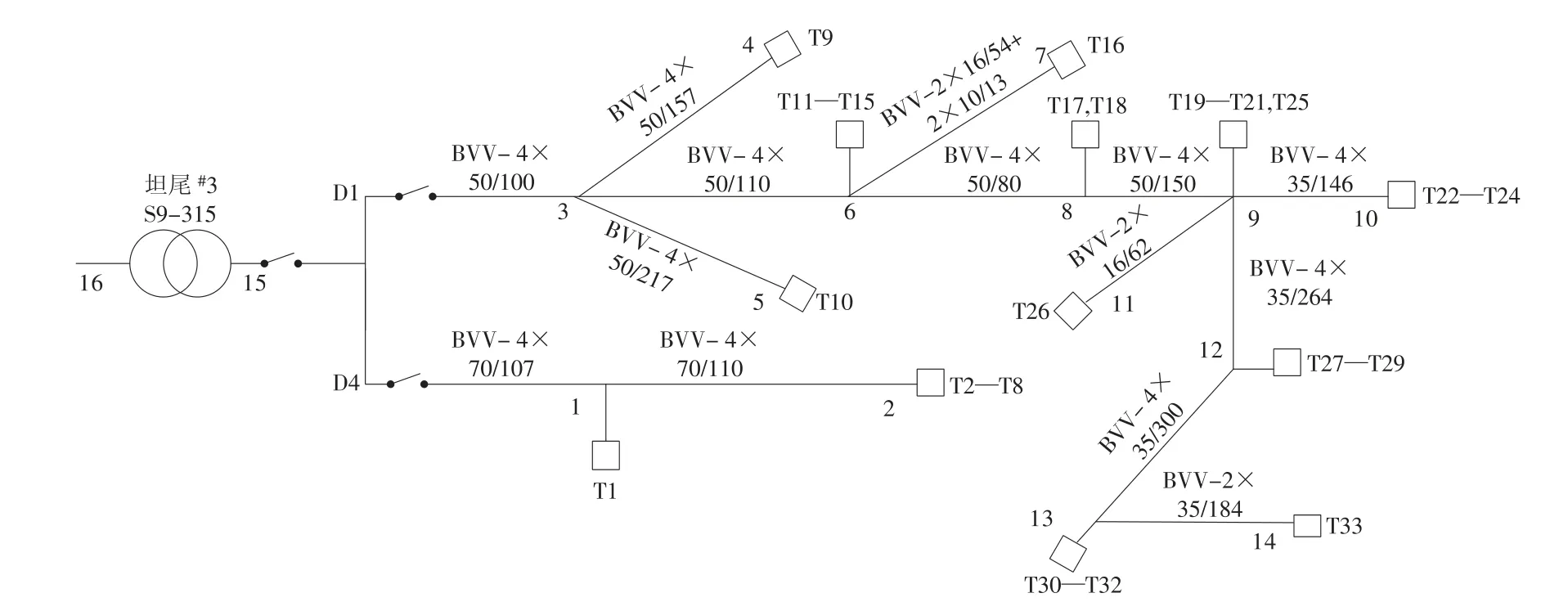
图1 某低压配电台区拓扑结构Fig.1 Topological structure of a low-voltage distribution network

以节点16为平衡节点，电压幅值设定为10.3 kV，相角为0°，其他节点为PQ节点。对台区进行确定性潮流计算，得到各节点电压数据，见表1。

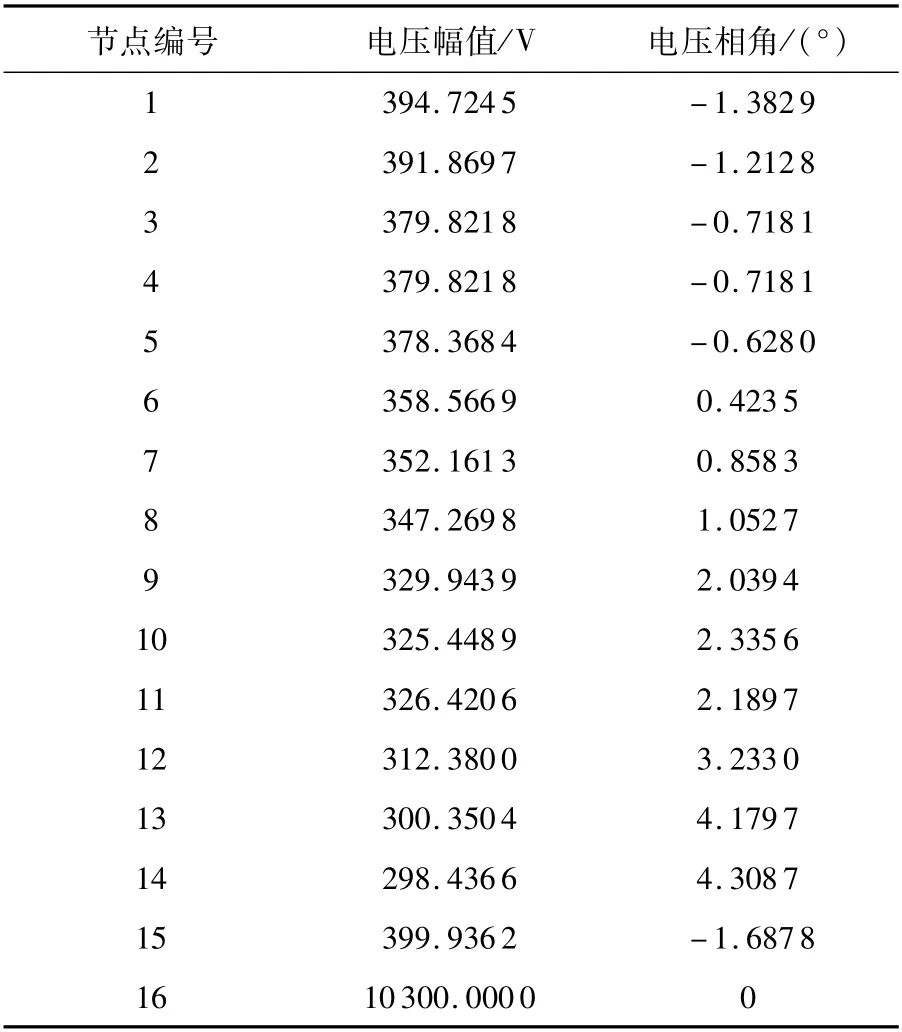
表1 无功补偿前台区各节点电压Tab.1 Voltage of each node in the distribution network before the reactive power com pensation

从表1可以看出，节点9—14的电压幅值已经无法达到配网供电电压不低于额定电压90%的要求。为提高供电电压水平，根据配电台区结构，选择分支较多的节点6、节点9以及供电线路较长的节点13作为分散无功补偿点，并给定各节点电压的初始区间，设定合适的迭代停止条件，采用经仿射运算改进的区间潮流算法，计算得到节点6，9，13的无功功率补偿区间及无功补偿后各节点电压幅值变化区间，见表2。

从区间潮流计算结果可以看出，在节点6，9，13进行一定范围的分散无功补偿后，可以使整个台区的电压得到改善，除节点13，14的电压下限略低于90%额定电压外，其他节点电压均可满足相关规范要求，能够保证农业用户的泵类负荷正常启动。

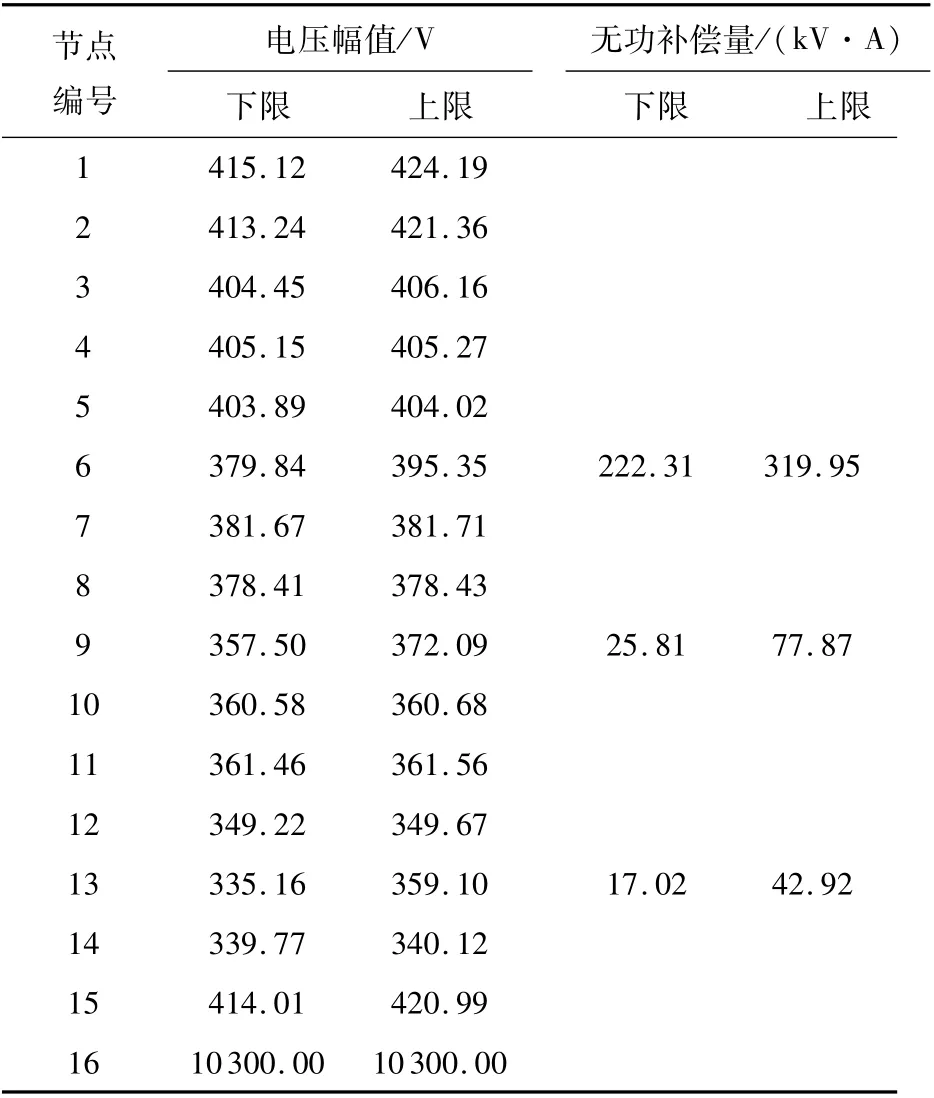
表2 无功补偿后台区各节点电压区间Tab.2 Voltage interval of each node in the distribution network after the reactive compensation

依据区间潮流计算结果，可为该配电台区确定无功补偿方案，见表3。

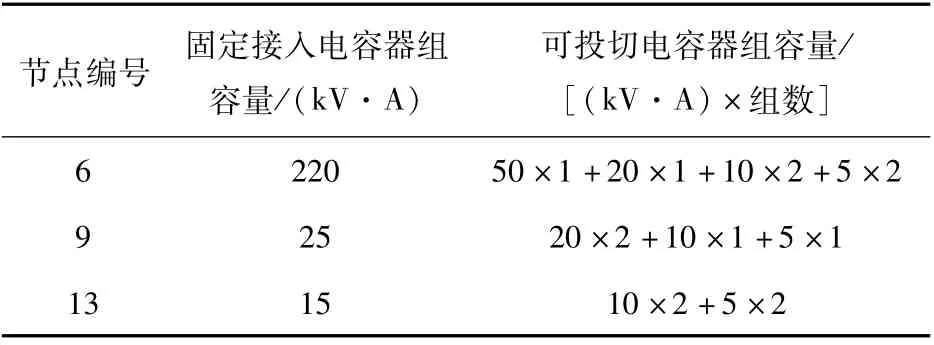
表3 配电台区无功补偿方案Tab.3 Reactive power compensation scheme in the distribution network

依据此方案指导供电企业为该台区设置无功补偿设备，配电自动化系统可根据实际情况灵活投切电容器组，可使整个台区的电压质量始终满足相关规范要求及用户需求。

4 结束语

本文提出的分散无功补偿优化方法得到的无功补偿方案考虑了配电台区负荷变动导致的潮流不确定性及电压不稳定性，借助优化的区间潮流计算模型，确定无功补偿的容量范围。

与单纯的分散无功补偿相比，本文提出的分散无功补偿优化方案能够适应一定范围的负荷变动，通过配电自动化系统灵活投切可调电容器组，使台区电压质量始终满足要求，提高了经济性。

对于分散无功补偿点的选择以及如何提高电压改善效果和进一步缩小投资，是后续的研究重点。