基于GA-SVM算法永磁同步直线电机变载荷进给位置误差的预测

于嘉龙,彭宝营*,侯明鹏,杨庆东

(1.北京信息科技大学机电工程学院，北京 100192;2.北京机科国创轻量化科学研究院有限公司，北京 100084)

永磁同步直线电机(permanent magnet synchronous linear motor，PMLSM)由于取消了中间传动环节直接产生直线运动，而具有高速、高精度、响应快、无反向间隙等优点，近年来得到越来越广泛的应用[1-3]。在永磁同步直线电机众多参数中，位置误差是衡量定位精度高低的重要指标。永磁同步直线电机广泛应用在高精度位置伺服系统中。在高速高精度的加工场合中，传统的机械传动方式已经无法满足当前高精度的要求，永磁同步直线电机具有高速的反应能力，是高速高精度进给系统的理想选择。但是，永磁同步直线电机没有传动机构，直线电机在进行高精度运动时会受到安装和外部干扰以及推力扰动的影响，会产生位置精度不准确，造成位置误差，影响高精度运动[4]。

近年来，中外学者的研究主要集中于位置误差对永磁同步直线电机的影响和位置误差的补偿方式。Yoshida等[5]提出了一种补偿圆柱型直线电机中霍尔元件线性位置传感器位置误差的新方法。补偿的特征是在初步测试中以恒定速度驱动动子时经过滤波的位置信号处理。Liu等[6]提出了一种基于滤波器和HFI(high frequency injection)系统中磁饱和交叉耦合的设计简单的直线电动机在线补偿方法。何良辰等[7]针对直线电机在运转过程中受到定位力扰动影响的问题，提出一种基于遗传算法优化神经网络的电机定位力辨识方法。该方法利用由加速度计得到的直线铁芯电机的定位力数据，通过人工神经网络进行建模，同时应用遗传算法对整个神经网络进行优化，完成对直线电机的定位力辨识。刘洪珍[8]针对数控机床中基于直线电机的工作台，利用神经网络建立直线电机轮廓误差模型，对影响轮廓精度的因素进行了分析与实验验证。现有研究大都是在理论层面分析误差的原因，然后通过补偿的方法来减小误差。而就如何实际预测位置误差的研究很少，现就如何准确预测永磁同步直线电机的变载荷位置误差进行相关的研究。

基于上述问题，提出使用遗传算法优化支持向量机建立永磁同步直线电机变载荷位置误差的预测模型，使用实验平台采集出来的数据进行训练，以正弦波信号的指令位置、指令速度和电流作为模型的输入，以三角波信号的位置误差作为模型的输出。利用遗传算法优化支持向量机，可以避免支持向量机模型的训练时间长、收敛速度较慢的问题，提高模型的鲁棒性和稳定性，已经被广泛应用于非线性预测中，并取得了良好的效果[9-11]。因此这里采用遗传算法优化支持向量机能够更好地寻找支持向量机的参数C和g，从而获得更准确的直线电机变载荷进给位置误差预测模型。

1 遗传算法优化支持向量机神经网络模型概述

1.1 直线电机变载荷位置误差支持向量机构建

支持向量机(support vector machine,SVM)回归算法是一种基于统计学习理论的函数逼近算法，是在分类支持向量机算法的基础上发展过来的，原理与支持向量机相似。支持向量机属于有导师的学习方式。支持向量机使用交叉验证网格法搜索的方法来寻找最佳支持向量机的参数惩罚因子C和核参数g[12-14]。

支持向量机建立永磁同步直线电机变载荷位置误差预测模型的基本思想是将实验所测的指令位置、指令速度和电流的数值变换到一个高维的特征空间后作为自变量，位置误差作为因变量。

对于直线电机给定了训练数据集(x1,y1),(x2,y2)。设SVR函数为

f(x)=ωφ(x)+b

(1)

式(1)中，ω∈Rn，b为权值；b∈R,为阈值；φ为将Rn空间的输入数据映射到高维空间的映射函数，设函数为

(2)

通过寻找最优ω、b在公式中固定不变的情况下最小化置信范围，得到的最优化问题为

(3)

s.t.yi-ωφ(xi)-b≤ξ+ξi

(4)

(5)

(6)

式(3)～式(6)的优化问题可通过引入拉格朗日函数将其转化为对偶问题，通过解对偶得到式(1)的解：

(7)

因为永磁同步直线电机预测模型只有三个变量需要确定，高斯径向基函数构造的支持向量机训练参数相对较少，容易确定参数，因而核函数采用高斯径向基函数，即：

(8)

在GA-SVM直线电机变载荷位置误差建模过程中，误差惩罚因子C、不敏感损失函数ξ和高斯径向基函数的参数σ对支持向量机(SVM)算法模型的精度预测有重要的影响。

通过理论分析，发现支持向量机在训练的过程中惩罚因子C和核参数g对支持向量机的泛化性能有很大的影响，所以需要调节这两个参数以改善支持向量机的泛化性能。

1.2 遗传算法参数设定

遗传算法优化支持向量机的基本思想就是首先通过遗传算法选择、交叉和编译并进行算法迭代，寻找并输出最优个体，按照编码规则进行解码，产生支持向量机的初始权值和阈值。然后将遗传算法优化得到的初始权值和阈值赋值给支持向量机，在进行网络的训练，最后可实现仿真预测[15-17]。遗传算法优化支持向量机参数的算法的流程如图1所示。

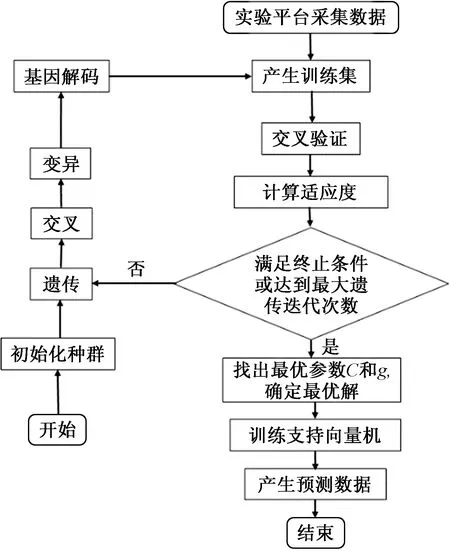
图1 遗传算法优化支持向量机流程Fig.1 Genetic algorithm optimization support vector machine flow chart

支持向量机模型构建完之后，使用遗传算法按照图1的流程对支持向量机的惩罚因子C和核参数g进行优化。兼顾运行时间和预测准确性，使用遗传算法优化支持向量机参数，遗传算法的参数如表1 所示。

表1 遗传算法主要参数Table 1 Main parameters of genetic algorithm

2 GA-SVM变载荷位置误差模型建立及结果分析

2.1 直线电机变载荷位置误差采集硬件平台

永磁同步直线电机变载荷位置误差数据采集平台包括控制系统、运动系统和采集系统，控制系统包括工业控制柜、PMAC(programmable multi-axis controller)运动控制器、伺服驱动器、上位机、数据总线；运动系统包括PSN型功率放大器、永磁同步直线电机、固定支座、加载装置；采集系统包括光栅尺、数据采集卡。

永磁同步直线电机变载荷位置误差实验装置主要硬件名称如表2所示。

表2 实验装置硬件型号Table 2 Main experimental device hardware model

通过上位机中PMAC自带的PEWIN32PRO软件进行运动指令的发送，将运动指令通过控制器的A/D转换发送到直线电机中，从而实现直线电机的运动。同时反馈检测元件将检测到的数据传送到上位机，PEWIN32PRO软件对数据进行分析研究从而实现实时误差的补偿。直线电机贴有光栅尺，用于检测直线电机的位置精度。

光栅尺测量获得直线位移信号，通过反馈装置传输到工控机中作为实时反馈信号。实验数据采集平台控制流程如图2所示。

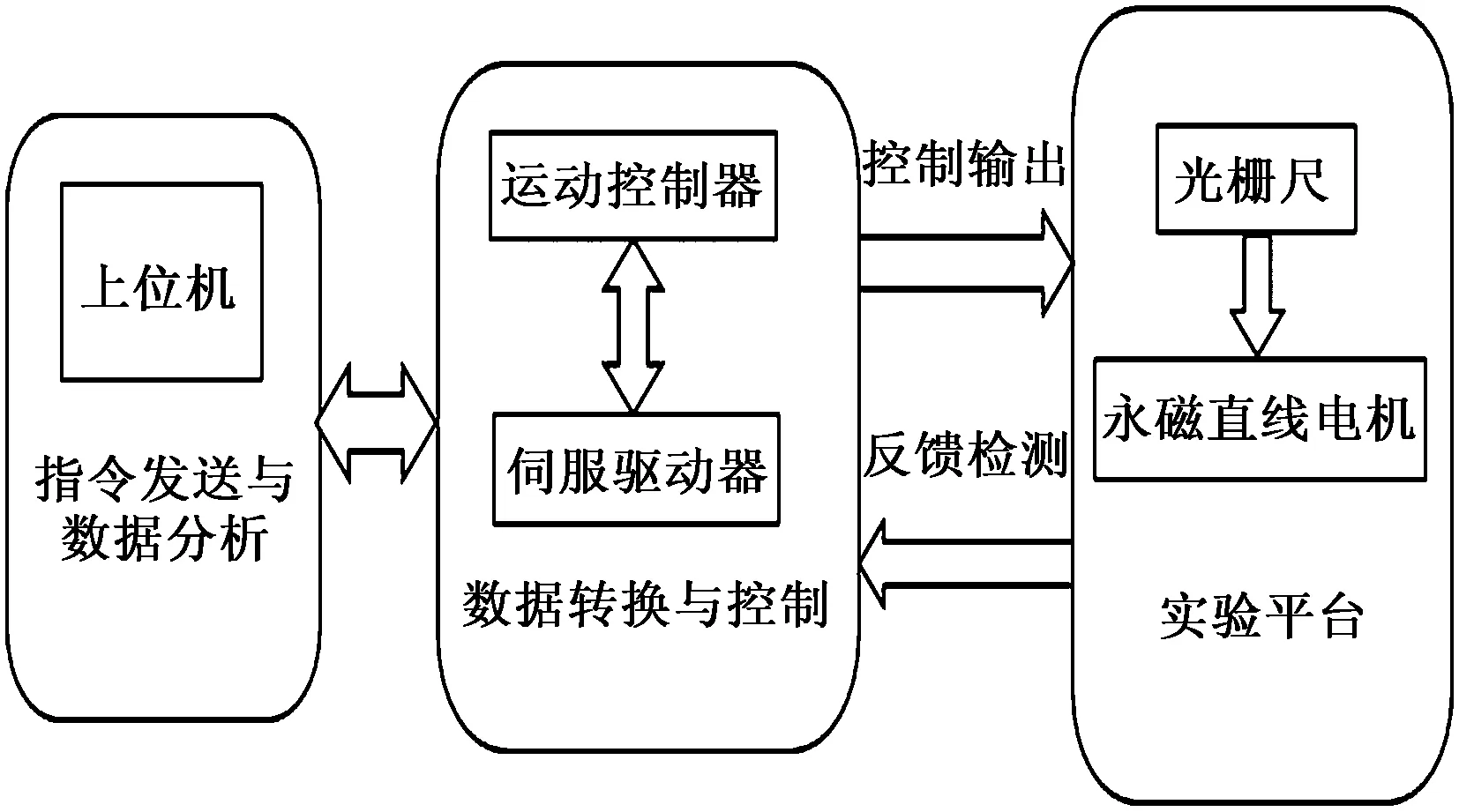
图2 实验采集平台控制流程Fig.2 Experimental acquisition platform control flow chart

其中，PMAC运动控制器是用来接收上位机的指令，并将控制指令通过伺服驱动器传给直线电机，通过数据采集卡、光栅尺来测量直线电机的位置并将数据传送上位 机进行分析和研究。用此方法来实现对直线电机的位置以及速度控制。还可以运用PMAC运动控制器自带的软件对直线电机进行PID整定以及对速度、位置、加速度等数据的采集与分析。

对永磁直线电机动子部分加上各种一定质量的负载，测定直线电机在不同负载和速度下的位置误差情况。现在将负载逐一加到力矩电机的转子部分，然后在运行直线电机，采集出来各种情况的多组数据，如图3所示为永磁同步直线电机变载荷位置误差实验平台设备图。实验中通过滑轮和缆绳增加配重的方法为直线电机加载，实验中的载荷有1、5、10、15、20 kg总共5种载荷,对于每种载荷的位置都进行了数据的采集。将各种情况的数据采集出来之后进行后期的数据处理，即把每一种情况的数据拿出50组数据进行汇总，使得在MATLAB软件拟合的训练集中包含各种负载数据，以达到更精确的训练模型。在MATLAB软件拟合的测试集的数据是将采集出来的数据随机的拿出60组，这种随机是确保在每一种情况下都有部分数据。

图3 实验采集平台设备图Fig.3 Experimental acquisition platform equipment diagram

2.2 直线电机变载荷位置误差GA-SVM模型构建

根据1.1节所述，可以建立支持向量机模型，首先先将试验所采集的数值通过式(3)变化到一个高维特征空间，变化完成之后，通过式(3)～式(6)求解出式(1)的最优解，将求解出的最优解在代入到支持向量机模型进行训练即可。

遗传算法采用图1所示流程不断地调节支持向量机的惩罚因子C和核参数g，使其能够充分发挥巡游的能力。首先进行数据的提取和预处理，然后利用gaSVMcgForClass函数对直线电机数据及进行SVM最佳参数的寻优，最终的适应度曲线如图4所示。

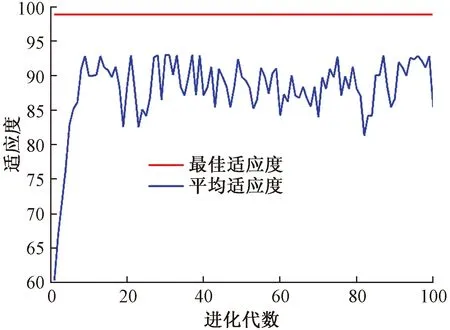
图4 利用GA寻找的最佳参数的适应度(准确度)曲线Fig.4 The fitness (accuracy) curve of the best parameters found by GA

由图4可知，利用遗传算法训练得到的最优参数惩罚因子为C=8.663 1，核参数为g=4.492 1。

2.3 直线电机变载荷位置误差预测结果

因为本文直接采集出来的数据范围比较大，可能导致模型的训练时间长，运行速度比较慢，所以在开始预测之前，要将数据进行归一化处理。将三个影响直线电机位置误差的数据和要输出的数据取[-1，1]之间的连续数值。归一化的处理公式为

Y=2(xi-xmax)/(xmax-xmin)-1

(9)

式(9)中，xmax是一组数据中的最大值；xmin是一组数据中的最小值；xi是当前值；Y为归一化之后的数据。

建立了GA-SVM预测模型，该模型以直线电机位置误差的各因素为输入,位置误差为输出。训练样本为直线电机平台实时采集的40组正弦波行走方式产生的运行数据，然后采用10组三角波行走方式产生的运行数据来验证模型的精确性。

建立了模型之后，经过MATALB软件进行预测，对直线电机变载荷进给位置误差模型进行仿真计算。

如图5所示为直线电机变载荷位置误差预测模型的遗传算法进化过程。从图5中可以看出，从第20代寻找到的最优个体函数值比较接近平均函数值，到第70代到达目标值，目标值为0.386 2。

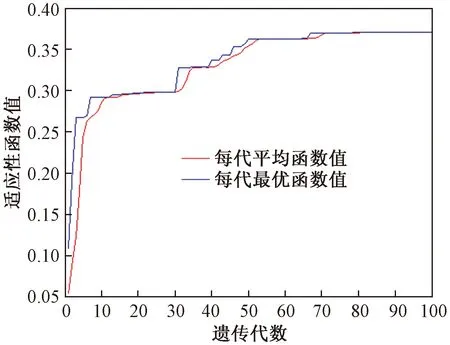
图5 遗传算法优化过程Fig.5 Genetic algorithm optimization process diagram

为了测试遗传算法优化支持向量机直线电机变载荷位置误差预测结果的优越性，选择基于BP神经网络的预测模型、基于Elman神经网络的预测模型与基于GA-SVM神经网络的预测模型进行对比，分别统计它们对永磁直线电机的预测精度，并从中抽取6组预测精度，结果如图6所示。

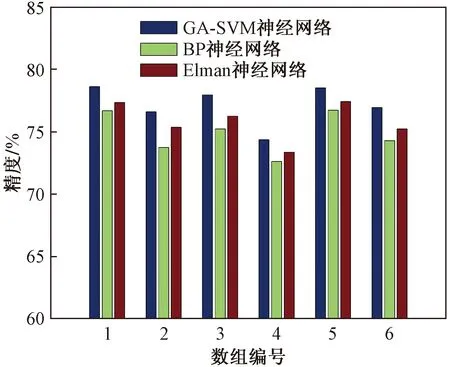
图6 与其他模型的位置误差预测精度对比Fig.6 Compares the accuracy of position error prediction with other models

从图6可以看出，相对于其他直线电机变载荷位置误差预测模型，遗传算法优化支持向量机神经网络具有较好的位置误差预测效果。从中抽取6组运行时间对比如图7所示，相对于其他神经网络预测模型，遗传算法优化支持向量机神经网络具有较好的预测效果，克服对比模型过拟合、误差大的缺陷，同时在实验过程中发现遗传算法优化支持向量机神经网络明显也要比其他的位置误差预测模型运行时间要快，明显提高了直线电机位置误差的预测效率。遗传算法优化支持向量机模型不需要计算网络连接权值等参数，所用时间短，且网络结构直接由数据样本决定，对网络训练影响不大，因此遗传算法优化支持向量机变载荷预测模型的工作时间可以满足高速高精度场合的要求。

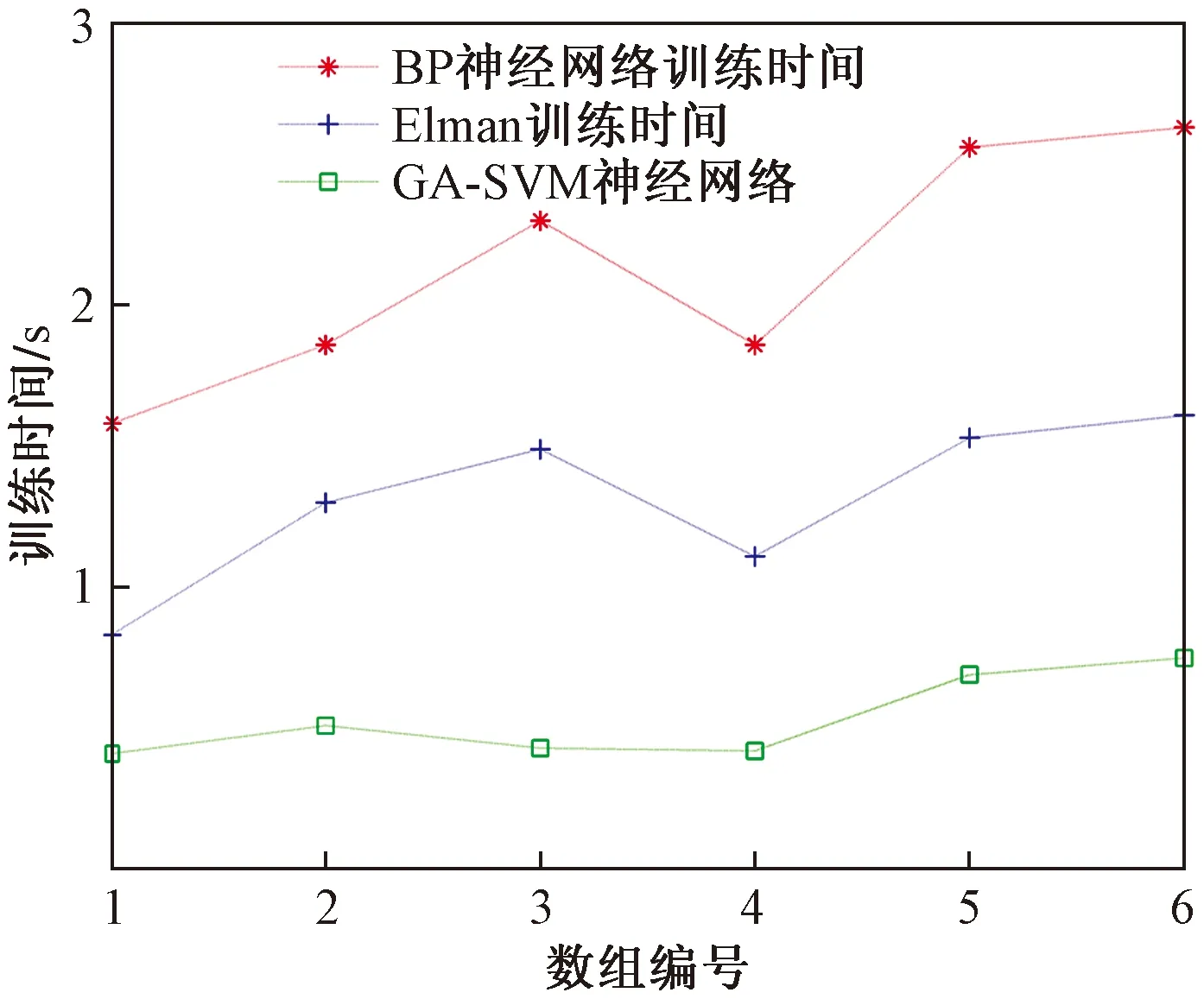
图7 与其他位置误差预测模型的预测运行时间对比Fig.7 Comparison of predicted run time with other position error prediction models

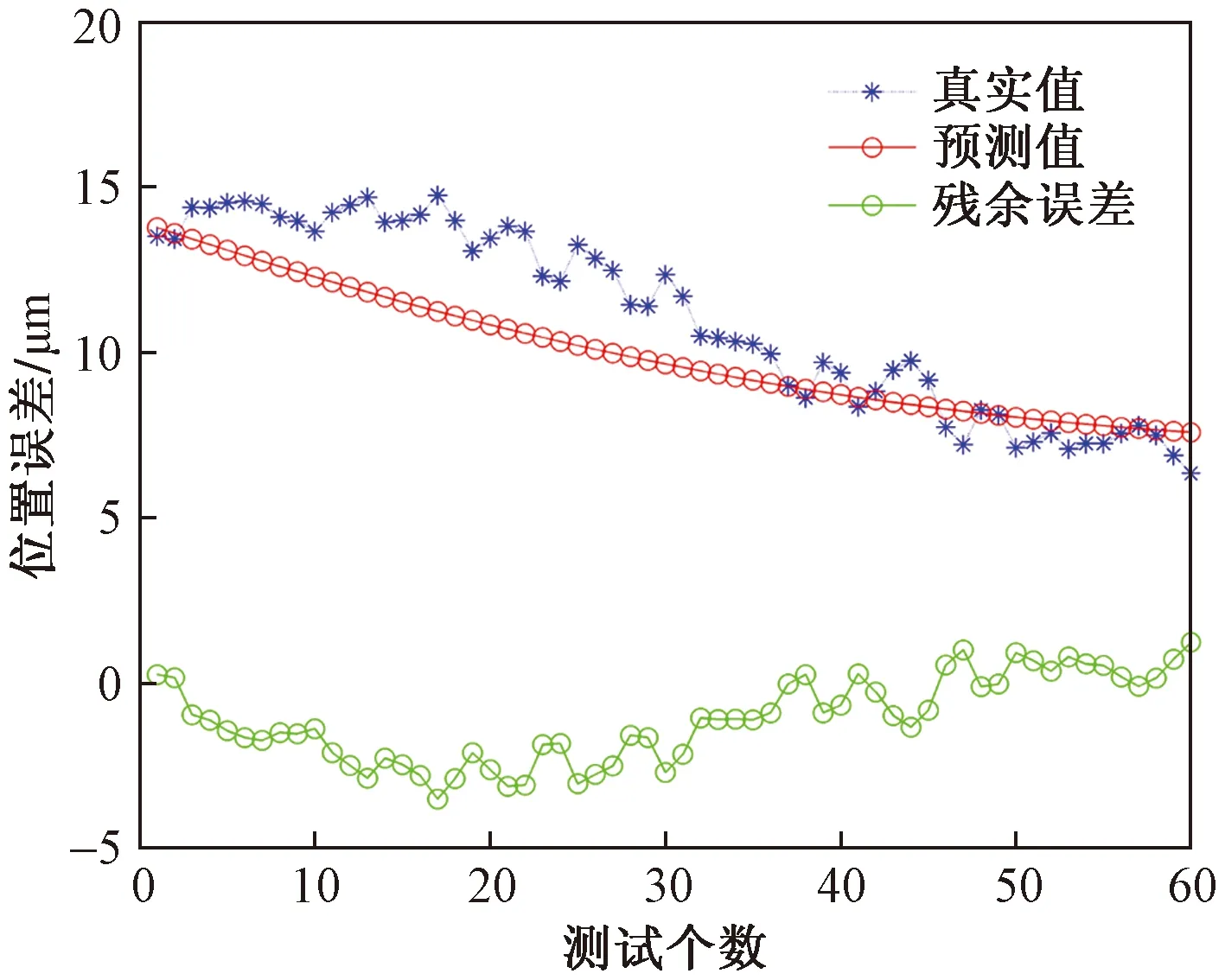
图8 未经GA优化的SVM直线电机预测模型Fig.8 SVM linear motor prediction model without GA optimization

本文有10组预测数据进行预测，其中只拿出一组典型的预测结果在图8和图9进行显示。图8是未经遗传算法优化支持向量机的直线电机预测位置误差图。加上遗传算法优化之后，仍然采用上一个模型使用的训练集和测试集，最终的预测结果如图9所示。

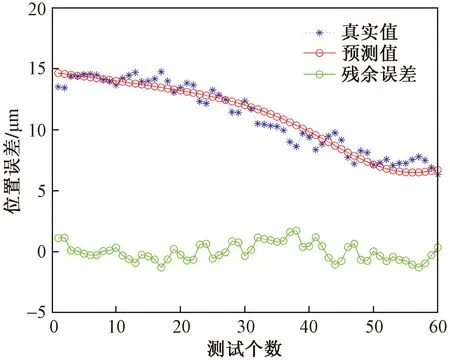
图9 经GA优化的SVM直线电机预测模型Fig.9 GA-optimized SVM linear motor prediction model

从图8可以看出，未经过遗传算法优化支持向量机的直线电机预测模型的最大残余误差是0.237 5 μm,经计算最大相对误差是1.703 8 μm，均方差为0.279 6 μm。而从图9可以看出，经过遗传算法优化支持向量机的直线电机预测模型的最大残余误差是0.179 1 μm，经计算最大相对误差是1.030 1 μm，均方差为0.186 3 μm。由此可知GA-SVM神经网络能够快速有效的预测出直线电机变载荷位置误差，提高了永磁同步直线电机变载荷位置误差的预测效率。

3 结论

位置误差作为衡量高精度系统的主要指标,对运动系统乃至整个永磁同步直线电机组都有着重大影响。准确快速地预测位置误差,能够对机械加工平台的稳定运行起到推动作用。本文提出的遗传算法优化支持向量机的设计方法，通过永磁同步直线电机实验平台采集数据生成训练样本和测试样本，构成了具有优化参数功能的支持向量机的预测模型，并与传统的BP模型和Elman模型进行对比。通过预测结果表明：

(1)使用遗传算法优化支持向量机神经网络的运行时间要低于传统的BP模型和Elman模型的运行时间。

(2)使用遗传算法优化支持向量机神经网络的精度要高于未使用遗传算法优化的支持向量机。

因此，对永磁同步电机变载荷位置误差的预测能够在一定程度上对整个直线电机系统的运行起到一定的指导意义。