基于五阶广义积分器的内置式永磁同步电机转子位置观测法

黄守道，陈婷，吴轩

（湖南大学电气与信息工程学院，湖南长沙 410082）

由于高功率密度、高效率、小体积、强鲁棒性等一系列优点，内置式永磁同步电动机（Interior Permanent Magnet Synchronous Motor，IPMSM）在工业领域中得到了广泛应用.而位置传感器的安装会增加IPMSM 控制的成本，同时降低系统鲁棒性.因此，近年来许多文献提出了多种无位置传感器控制策略，它们大体上可以被分为两类：其一为高频注入法[1-3]，主要适用于零速和低速工作状态；另一种则是反电动势（Electromotive Force，EMF）法[4-14]，因反电动势幅值与电机转速成正比，故而将其主要用于电机中高速运行状态.本文中，采用的是基于扩展反电动势（EMF）的滑模观测器（Sliding Mode Observer，SMO）.

通常，利用滑模观测器法所得的反电动势误差主要包括两方面：直流偏移和谐波成分.其中，直流偏移往往由参数不匹配、变换器非线性、积分初值不定和检测误差导致[15].在IPMSM 驱动系统的控制过程中，坐标变换和解耦是非常关键的步骤，而逆变器非线性、磁场空间谐波、参数不匹配等均会导致转子位置观测值中存在大量谐波误差，使得坐标变换不准确以及解耦不完全，进而令电流产生谐波以及转矩产生脉动，最终增加驱动系统的不必要消耗，降低系统的控制性能.如今，针对上述转子位置误差，已经提出了一些改善方案.文献[16]提出根据磁场空间谐波进行精确建模，但该方法在参数变化时的可靠性不高；文献[17]提出了采用梯形波补偿电压对逆变器非线性进行补偿.然而，建立仅仅考虑逆变器非线性补偿或是磁通空间谐波的数学模型，难以完全消除IPMSM 无传感器控制时的位置观测误差.因此实际需要的是，能够在电机转速多变的情况下仍然能够有效消除脉动误差的位置观测法.

基于上述需求，本文提出五阶广义积分器（Fifth-Order Generalized Integrator，FOGI）[18-20].采用传统广义积分器的非直接串联，并且外加了直流滤除，通过重新搭建反馈通道，最终组成五阶广义积分器.该模块具有3 个系数，根据不同的调整幅度，可达到不同要求的响应速度及带通特性.相比文献[4]提出的二阶广义积分器（Second-Order Generalized Integrator，SOGI）法，五阶广义积分器不受增益单一的影响，可以在提升谐波衰减能力的同时缩短系统的稳定时间.且文中给出了一种简单可靠的参数选择方法，解决了高阶方程参数整定复杂的难题.

本文所研究的基于五阶广义积分器的转子位置观测策略从基于扩展反电动势法的定子电流滑模观测器中检测出反电动势信息，在锁频环（Frequency Locked Loop，FLL）[21-23]的协调工作下，经过五阶广义积分器滤波后，再将其输入锁相环（Phase Locked Loop，PLL），该方法能够有效抑制反电动势观测值中的谐波和直流偏置，提取更为精确的基波信号，进而消除转子位置信息中的谐波误差，改善IPMSM 无位置传感器控制性能.

1 IPMSM 无传感器控制系统

1.1 基于滑模观测器的IPMSM 无传感器控制

IPMSM 无位置传感器控制系统结构图如图1 所示，系统采用转速、电流双闭环控制.由滑模观测器获取α-β 轴系下的反电动势观测值，而后通过五阶广义积分器提取基波分量作为锁相环的输入信号，最终获得转速、转子位置信息.

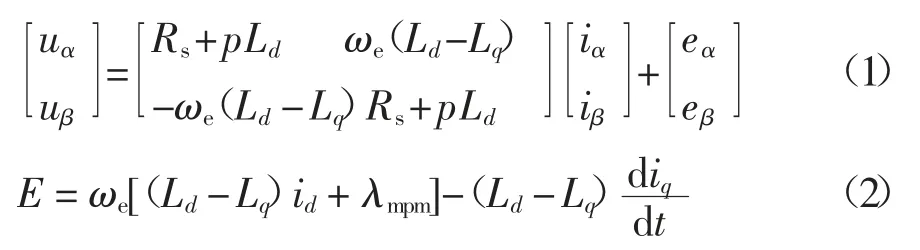
式中：Rs为定子电阻；下标α、β 分别代表α、β 轴；u、i分别为定子电压、电流；Ld、Lq均为两相旋转坐标系（d-q 轴系）的电感；p 为导数算子；ωe为转子电角速度；eα、eβ均为反电动势，其中eα=E（sinθr）、eβ=E（cosθr）；id、iq表示d-q 轴系的定子电流；θr为转子位置角度；E 为反电动势幅值；λmpm为永磁体磁链幅值.

图1 IPMSM 无位置传感器控制系统结构图Fig.1 Scheme of IPMSM sensorless control system

根据式（1），构建定子电流滑模观测器：

通过上述的定子电流滑模观测器，可以获得反电动势观测值.通常采用PLL 代替反正切函数获取转子位置观测量，能够在一定程度上抑制高频噪声，提高转子位置观测结果的精度.

1.2 转子位置误差分析

由于逆变器死区时间以及IPMSM 中存在磁链空间谐波的影响，导致定子电流中存在6k±1 次谐波，其表达式为：

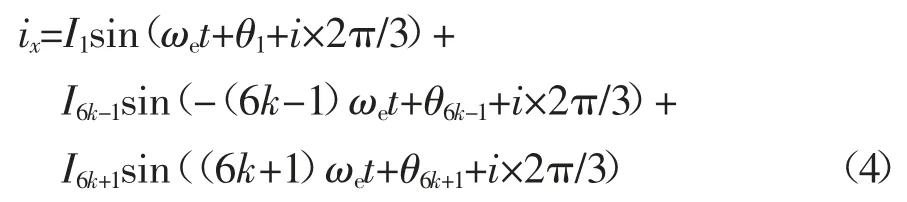
式中：x 代表a、b 和c 相；i 可表示0、1、2；下标1、6k-1、6k+1 表示相应的谐波次数；I 为定子电流的幅值；θ 为定子电流的初始相位.使用Park 和Clark 变换后，将定子电流变换到d-q 轴系下：

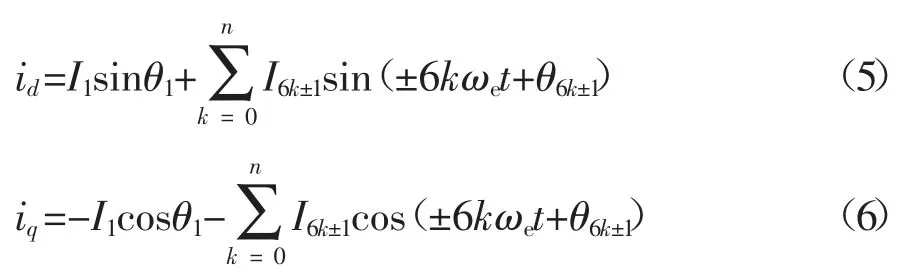
根据式（5）（6）可知，与α-β 轴系下的6k±1 次谐波对应的是d-q 轴下的6k 次谐波，将其代入式（2）中，得到反电动势为：

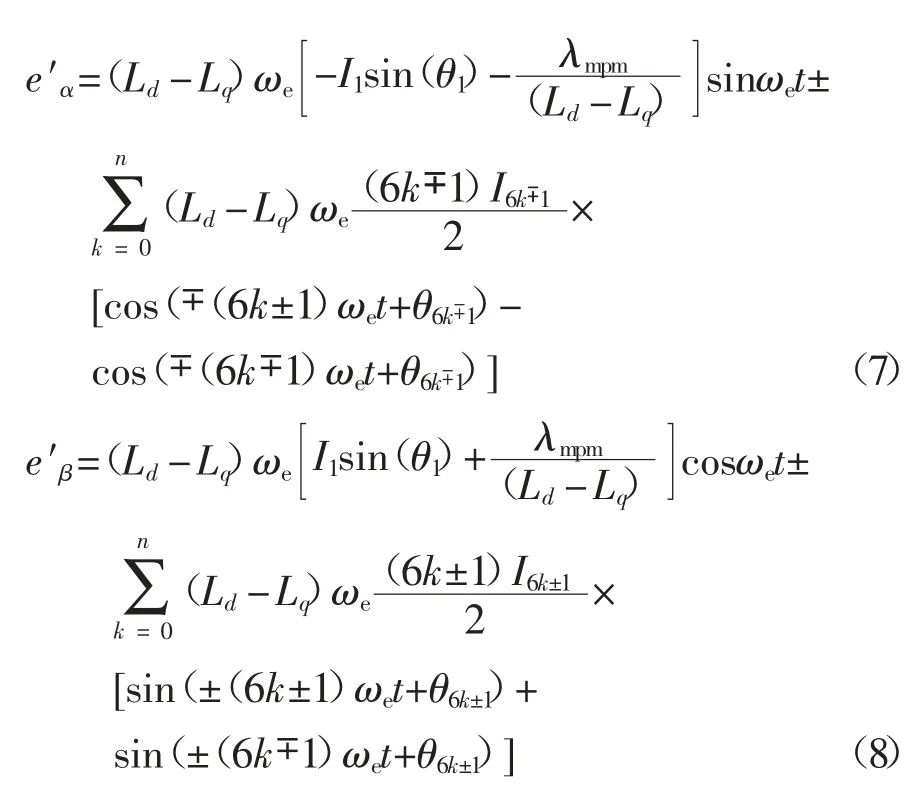
由式（7）（8）可知，反电动势观测量包含基波、高次谐波，为简便说明，将其表达成如式（9）和式（10）所示，其中e′f和e′h分别代表反电动势的基波检测量和谐波检测量分别为6k-1 次和6k+1 次谐波的幅值；θe（6k-1），θe（6k+1）是相应的初始相位.

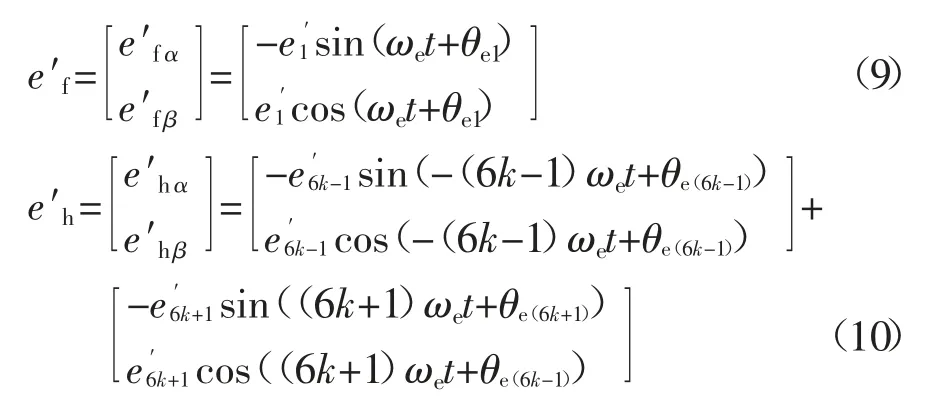
图2 为正交锁相环位置观测器结构框图，假设滑模观测器和锁相环都收敛，可将等效误差ε0及其近似值表示为：

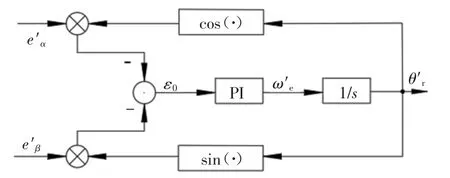
图2 正交锁相环结构框图Fig.2 Structure diagram of quadrature PLL

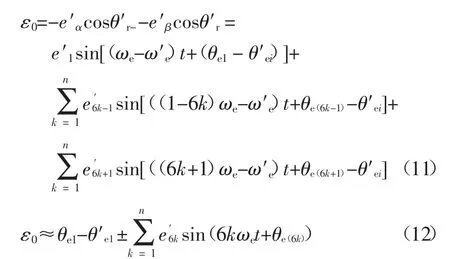
式中：ω′e、θ′r分别表示由PLL 获得的转子电角速度、位置观测值，且θ′r=ω′et+θ′ei；θ′ei为反电动势初始位置估测量；e′6k为反电动势的等效6k 次谐波幅值；θe1、θe（6k）分别代表反电动势基波、6k 次谐波初始相位.根据式（12）可以看出：6k 次谐波脉动作为附加误差分量存在于相位误差中.

在MATLAB/Simulink 中进行IPMSM 无传感器控制系统仿真，图3 为在600 r/min、额定负载下无自适应滤波时的位置观测仿真波形.由图3 可知，位置观测值中主要存在6 次谐波分量.无法直接观察到更高次数的谐波分量是因为它们所占比重不大.

图3 在600 r/min、额定负载下无自适应滤波时的位置观测仿真波形Fig.3 Simulation waveforms of estimated position without adaptive filter at 600 r/min and rated load

2 五阶广义积分器

为消除转子位置中的谐波脉动误差，提出基于五阶广义积分器的滑模观测器法.凭借锁频环的作用，该控制策略能够实时跟踪锁定电机运行速度，滤除反电动势谐波、直流分量，提取基波成分，进而抑制位置观测量中的谐波误差，提高观测结果的精度.

2.1 五阶广义积分器

图4 为五阶广义积分器基本结构框图，输出信号e′和输入信号e 间的关系为：

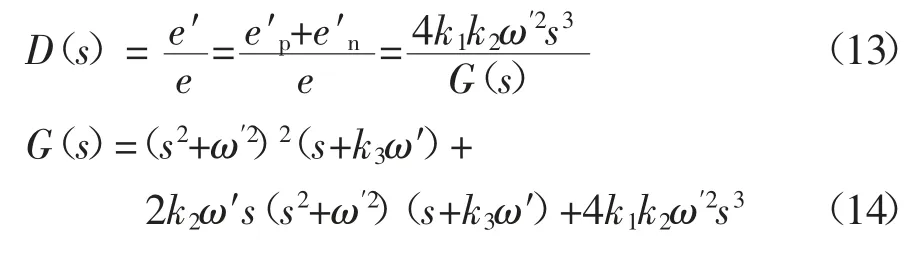
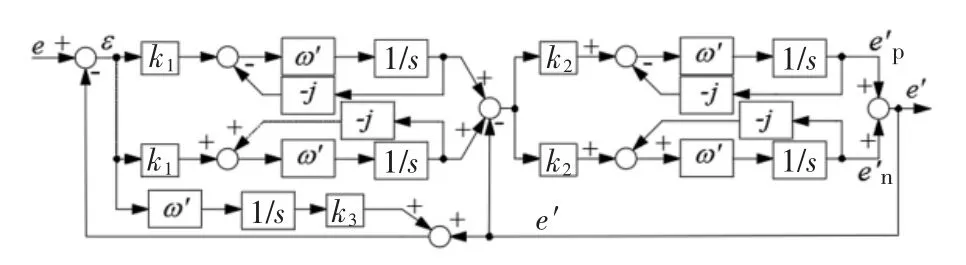
图4 五阶广义积分器基本结构Fig.4 Basic structure of the FOGI

由图5 所示的D（s）伯德图可知，D（s）具有较强的带通滤波器特性，故而能够抑制反电动势观测量中的谐波及直流偏置，其通带中心频率为五阶广义积分器的谐振频率ω′，滤波能力由误差放大参数k1、k2以及旁路回路增益k3共同确定.其中k1与k2作用类似，故只展示其中之一变化时的伯德图.即，增大k1或k2对应稳定时间缩短，带宽增大，对频率的敏感性降低；反之则收敛速度降低，滤波性能提升.k3变化时的伯德图如图6 所示，若k3增大，则五阶广义积分器收敛速度加快，且直流成分衰减能力增强，但同时将加剧输出信号的阻尼效应.

图5 不同k1 时的五阶广义积分器伯德图Fig.5 Bode diagrams of FOGI with different k1

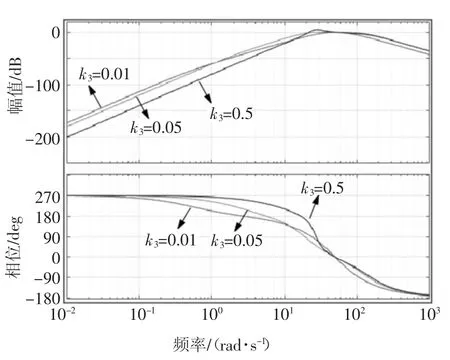
图6 不同k3 时的五阶广义积分器伯德图Fig.6 Bode diagrams of FOGI with different k3

根据式（13）（14）可知，输出信号e′的频率等于谐振频率ω′.当且仅当谐振频率与输入信号e 的基波频率ω 相等时，能够获得与输入信号幅值相同的输出量.故而，若将反电动势检测值输入五阶广义积分器，便可提取其基波成分.五阶广义积分器中的谐振频率由锁频环调谐，确保谐振频率与输入信号频率ω 实时相等.锁频环结构框图如图7 所示.根据锁频环的频率自适应性可将其简化为一阶频率自适应环，传递函数如式（15）所示，其响应速度由增益T 唯一确定.

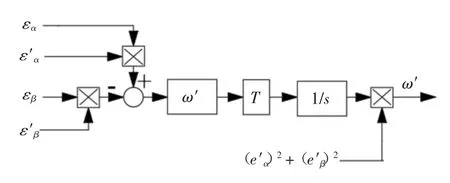
图7 锁频环结构框图Fig.7 Block diagram of FLL

2.2 参数设计

五阶广义积分器的较高阶数，使其呈现出比其余低阶滤波器更佳的滤波特性，因此在滤除谐波（主要为5、7 次）和直流分量上具有独有的优势.然而，更高的阶数往往意味着更多的参数和更复杂的整定，但在本节中讨论一种简单的调谐方法，在给出所有参数的最佳值后，与相应的传统二阶广义积分器及伯德图对比，体现五阶广义积分器所具备的优势.

为了简化复杂的参数整定过程，引入控制原理中的五阶标准特征方程，将五阶广义积分器的特征方程与之比较，同时绘制不同参数时的伯德图进行对比，提出一种简单可靠的参数选择方法.五阶标准特征方程如下：

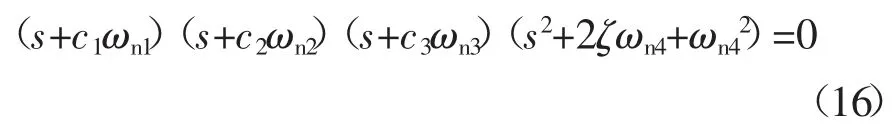
式中：ζ 为阻尼因子，其值为ζ=0.707；ωn1、ωn2、ωn3、ωn4表示标准特征方程各个极点振荡的固有频率；c1、c2、c3均为常系数.为最大程度简化参数整定过程，本文中取c1=c2=1、c3=0.05，并假定所有极点的振荡频率为ωn1=ωn2=ωn3=ωn4=2π×50 rad/s.为获得五阶广义积分器中各个参数的值，将式（14）与式（16）进行系数比较[19]，最终整定五阶广义积分器的参数依次为：k1=0.78，k2=1.56，k3=0.05.

根据文献[4，19，22]可知，传统二阶广义积分器传递函数为：

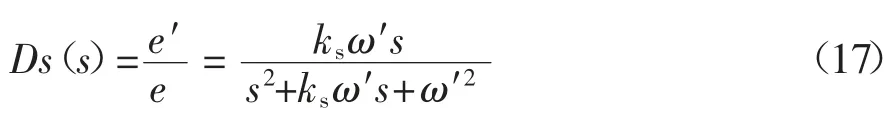
式中：ω′表示二阶广义积分器的谐振频率，同时也是其输出信号频率；ks为系统增益，本文令二阶广义积分器系统增益ks=.绘制二阶、五阶广义积分器伯德图如图8 所示；依次给二者输入单位幅值的50 Hz 正弦波信号，通过其输出响应波形对比二者稳定时间，如图9 所示.

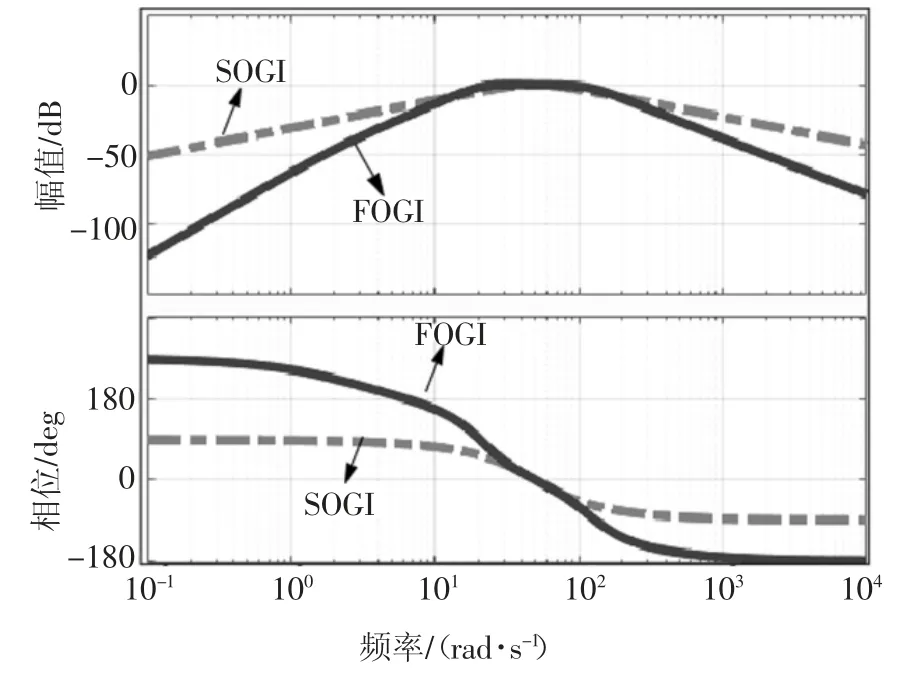
图8 SOGI 和FOGI 的伯德图Fig.8 Bode diagrams of SOGI and FOGI

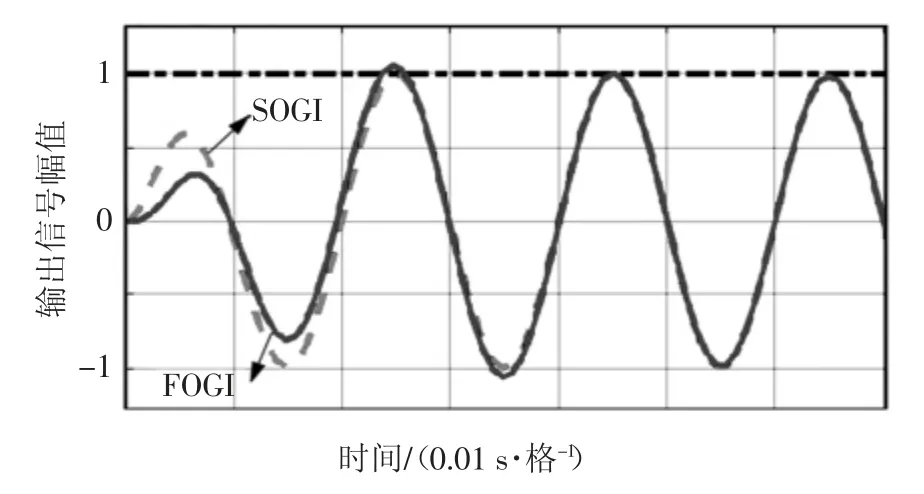
图9 SOGI 和FOGI 的响应曲线Fig.9 Response curves of SOGI and FOGI

根据图8 和图9 对比可知，不论是在谐振频率点以上或是以下，五阶广义积分器都表现出了比二阶广义积分器更好的谐波衰减能力，且此时二者的动态响应速度基本相同.由此可得，五阶广义积分器经过合理的参数设计，具备抑制反电动势扰动成分，提高转子信息检测精度的能力；且在动态响应或是稳态控制上都呈现出了优于二阶广义积分器的控制性能，该结论将在下述恒速、变速、变载实验中证明.

3 仿真与实验

3.1 仿真波形

在MATLAB/Simulink 仿真环境下建立基于五阶广义积分器的滑模观测器模型.电机及其余控制参数设置如表1 所示，其中仿真、实验所用电机参数、控制参数相同.由于仿真过程中，使用的是库中自带的理想电机模块，因此需要人为添加扰动.磁场空间谐波需要对电机模型进行改造，过程复杂，故本文中在SVPWM 中添加Simulink 的ON delay 模块，模拟逆变器非线性.

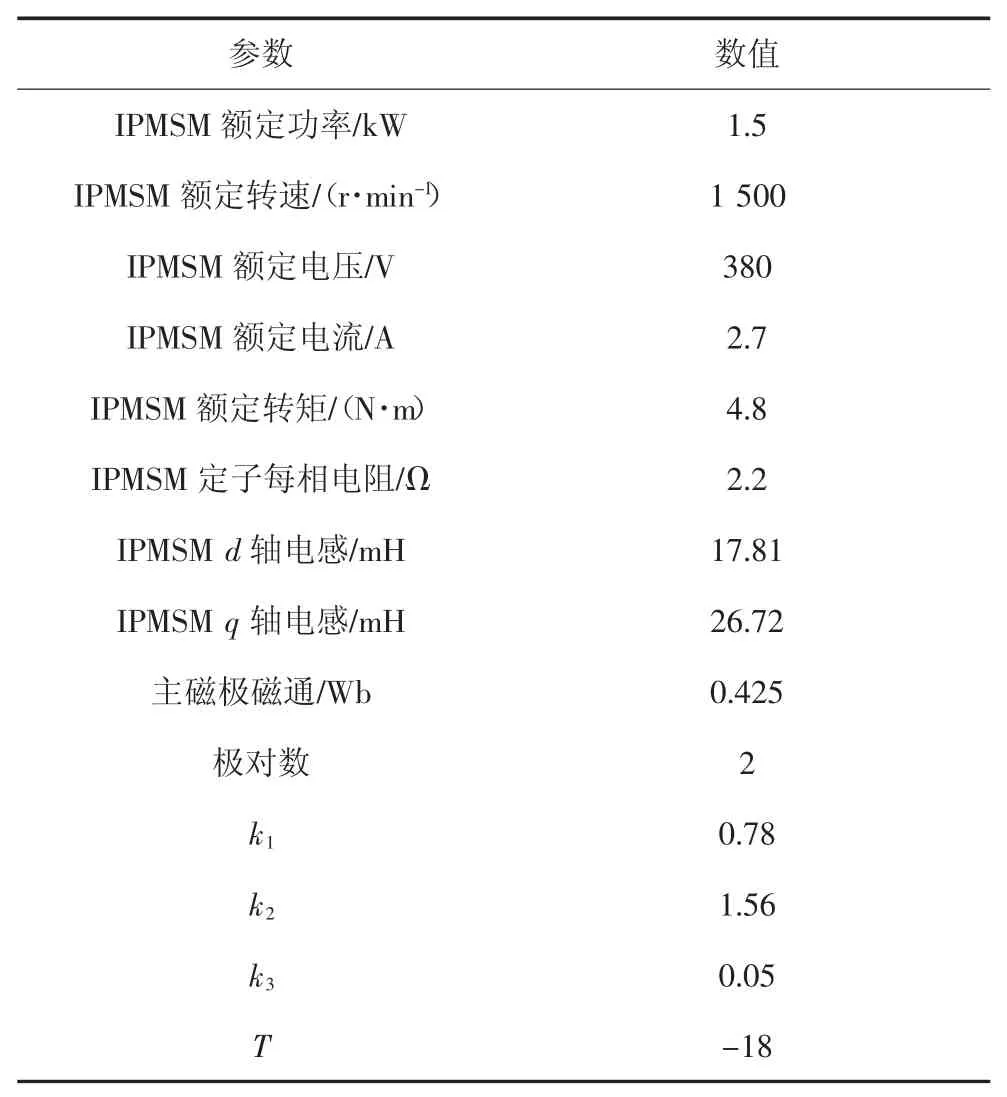
表1 仿真及实验参数Tab.1 Parameters of simulations and experiments

令电机以600 r/min、100%额定负载运行，图10为仿真时的反电动势观测量及其傅里叶分析波形.图10（a）（b）分别为五阶广义积分器使能前后的仿真结果，从上至下依次为α 轴反电动势观测波形、快速傅里叶（Fast Fourier Transform，FFT）分析结果.由图10 可知，引入五阶广义积分器后，反电动势中的直流成分和5、7、11、13 次谐波明显减少，反电动势的波形也更为平滑，且α 轴反电动势总谐波畸变率（Total Harmonics Distortion，THD）由使能前的17.1%降低为12.18%.

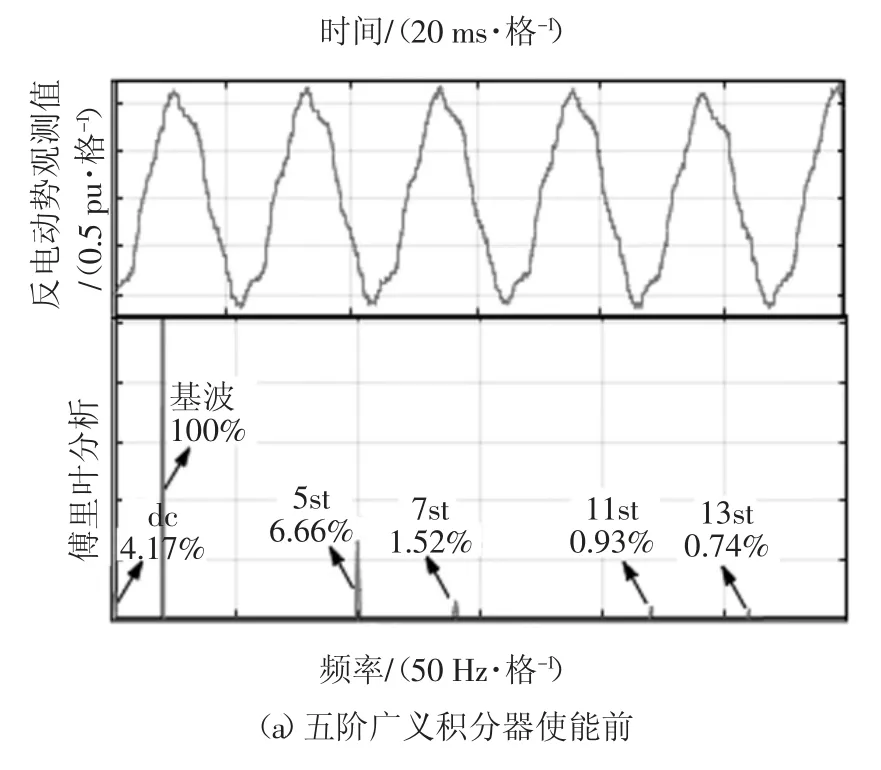
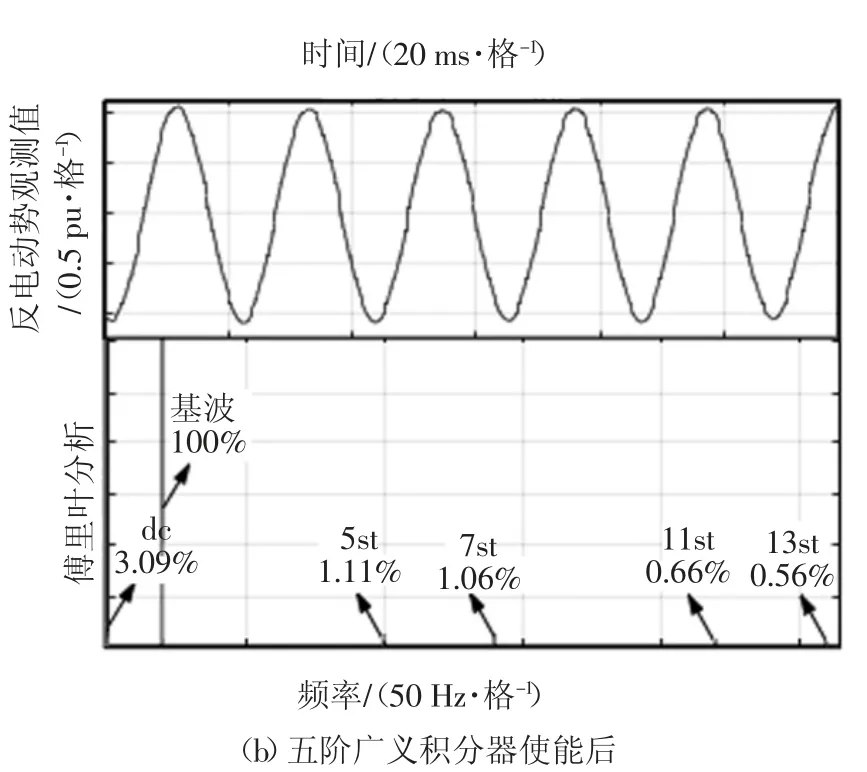
图10 仿真时的反电动势观测值及其傅里叶分析Fig.10 EMF estimates and the FFT analysis in simulation

图11 为600 r/min、100%额定负载情况下位置观测值和转速观测值仿真结果.自上而下依次为位置观测值和转速观测值.虚线左、右两侧分别为五阶广义积分器使能前、后的仿真结果.经过对比可知，五阶广义积分器使能后，位置观测值无明显6 次谐波，波形变得更加平滑，且转速波形在使能后脉动幅度显著降低.

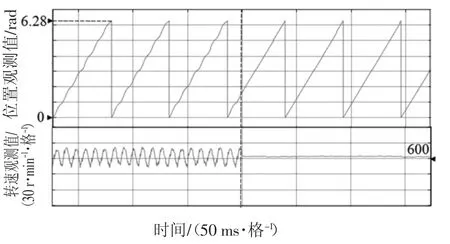
图11 在600 r/min、100%额定负载下的位置观测值和转速观测值仿真结果Fig.11 Simulation waveforms of position estimates and speed estimates at 600 r/min，100%rated load

3.2 实验结果

为验证基于五阶广义积分器的滑模转子位置观测法的有效性及相对于二阶广义积分器的优势，在1.5 kW dsPACE 半实物实验平台上，对IPMSM 矢量控制系统进行研究.

图12 为在600 r/min、100%额定负载下实验时的反电动势观测值及其傅里叶分析.图12（a）和图12（b）分别为五阶广义积分器使能前和使能后的结果.由图12 可知，五阶广义积分器使能前，反电动势观测值存在明显的6k±1 次谐波，根据其FFT 分析结果可知，其中5 次、7 次幅值较大，为主要谐波分量.经过五阶广义积分器滤波后的反电动势波形如图12（b）所示，由于5、7、11、13 次谐波和直流偏置均得到了有效的抑制，反电动势波形变得光滑，无明显波动.

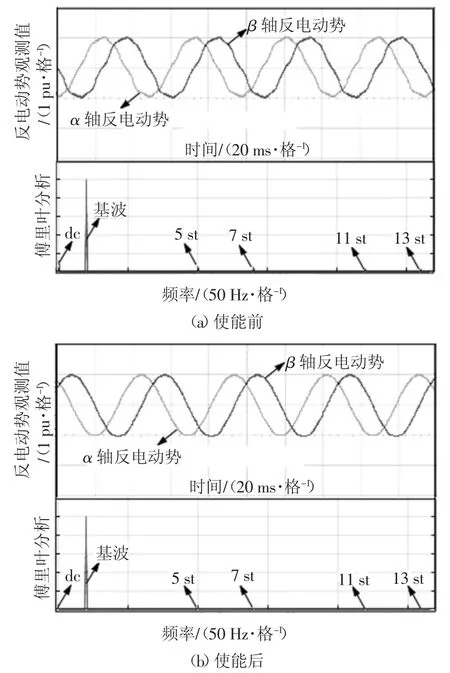
图12 在600 r/min、100%额定负载下实验时的反电动势观测值及其傅里叶分析Fig.12 EMF estimates and the FFT analysis at 600r/min，100%rated load in experiment

将观测得到的α、β 轴反电动势数据导入MATLAB，绘制五阶广义积分器使能前后的反电动势李萨如图，如图13 所示.由图13 可知，五阶广义积分器使能后，李萨如图由类六边形变为圆形，脉动程度明显减小，谐波成分显著降低.

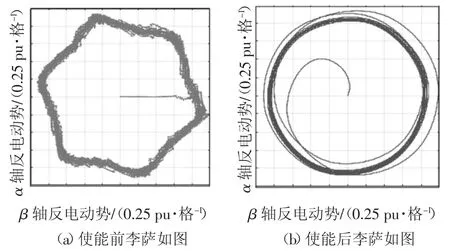
图13 五阶广义积分器使能前后的反电动势观测值李萨如波形Fig.13 Lissajous waveform of the EMF estimates with and without the FOGI

图14 为在转速是600 r/min、100%的额定负载下电机无位置传感器运行时，二阶广义积分器、五阶广义积分器分别使能后的实验结果，从上至下依次为位置观测值及位置观测误差.由图14 可知，二阶广义积分器使能时转子位置观测波形不平滑，波动显著，转子位置误差中存在较大的6 次谐波，其最大值可达0.04π rad.五阶广义积分器使能后，转子位置观测波形变得更加平滑，位置观测误差中的6 次谐波明显减小，其最大值仅为0.018π rad.

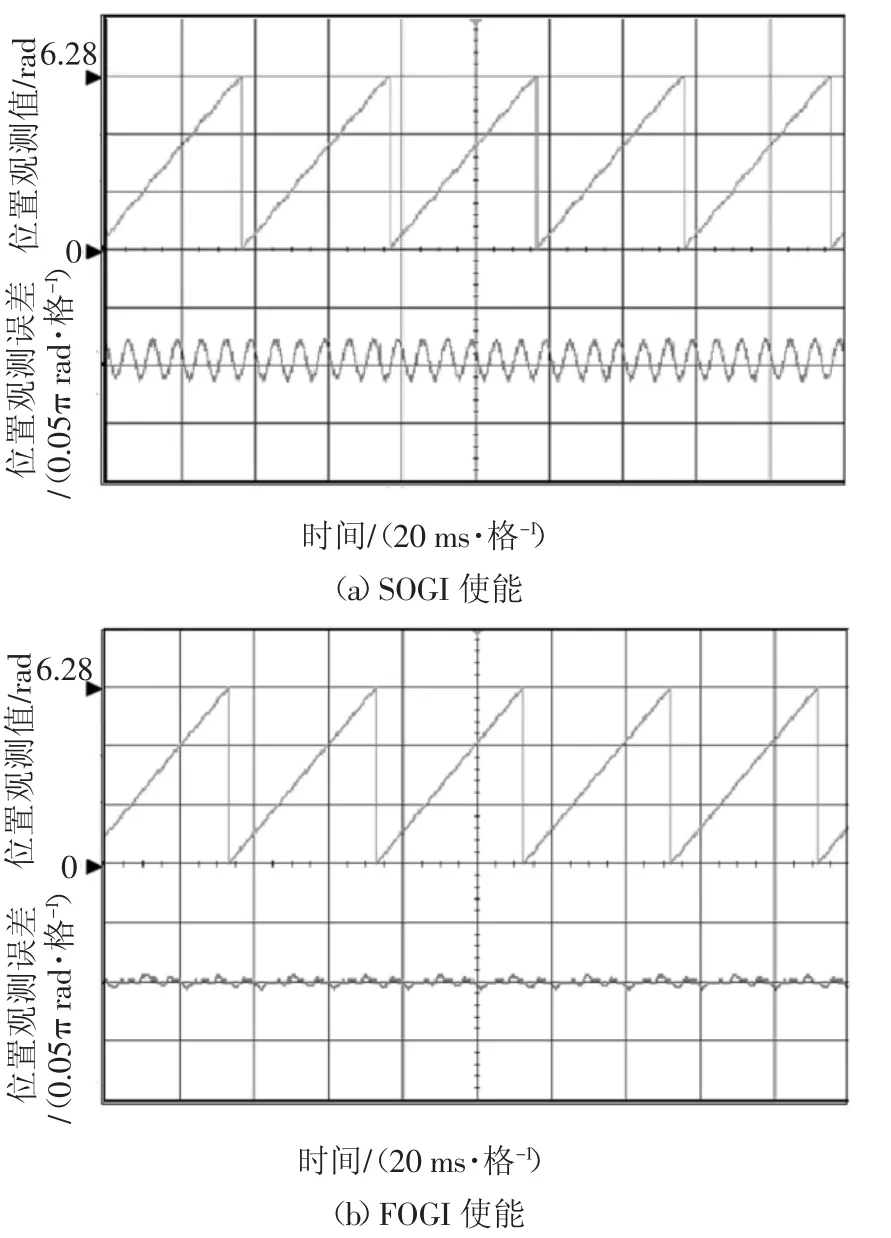
图14 位置观测值、位置观测误差实验波形Fig.14 Experimental waveforms of position estimates and position estimation error

为了进一步验证五阶广义积分器相对于二阶广义积分器的优势，进行变速、变负载时二阶、五阶广义积分器分别作用下的实验.图15 为在25%的额定负载下，转速由600 r/min 上升到1 200 r/min，而后又降到600 r/min 时的加减速实验波形.图15（a）和图15（b）分别表示二阶广义积分器、五阶广义积分器使能后的结果，各图自上而下依次为转速观测值ω′e、转速观测误差Δω′e、位置观测误差Δθ′r.对比实验结果可知，在五阶广义积分器使能后，转速波形波动幅度减小，波形变得更加平滑，位置观测误差最大值由0.035π rad 减至0.016π rad.

图16 为在600 r/min 的恒定转速下，负载值由50%额定负载上升至100%额定负载，而后又降至50%的加卸载实验波形.图16（a）和图16（b）分别表示二阶广义积分器、五阶广义积分器使能后的结果，各图自上而下依次为转速观测值ω′e、转速观测误差Δω′e、位置观测误差Δθ′r.对比实验结果可知，在五阶广义积分器使能后，转速观测误差最大值由16 r/min降至7 r/min，转速波动幅度、位置观测误差均得到明显减小.

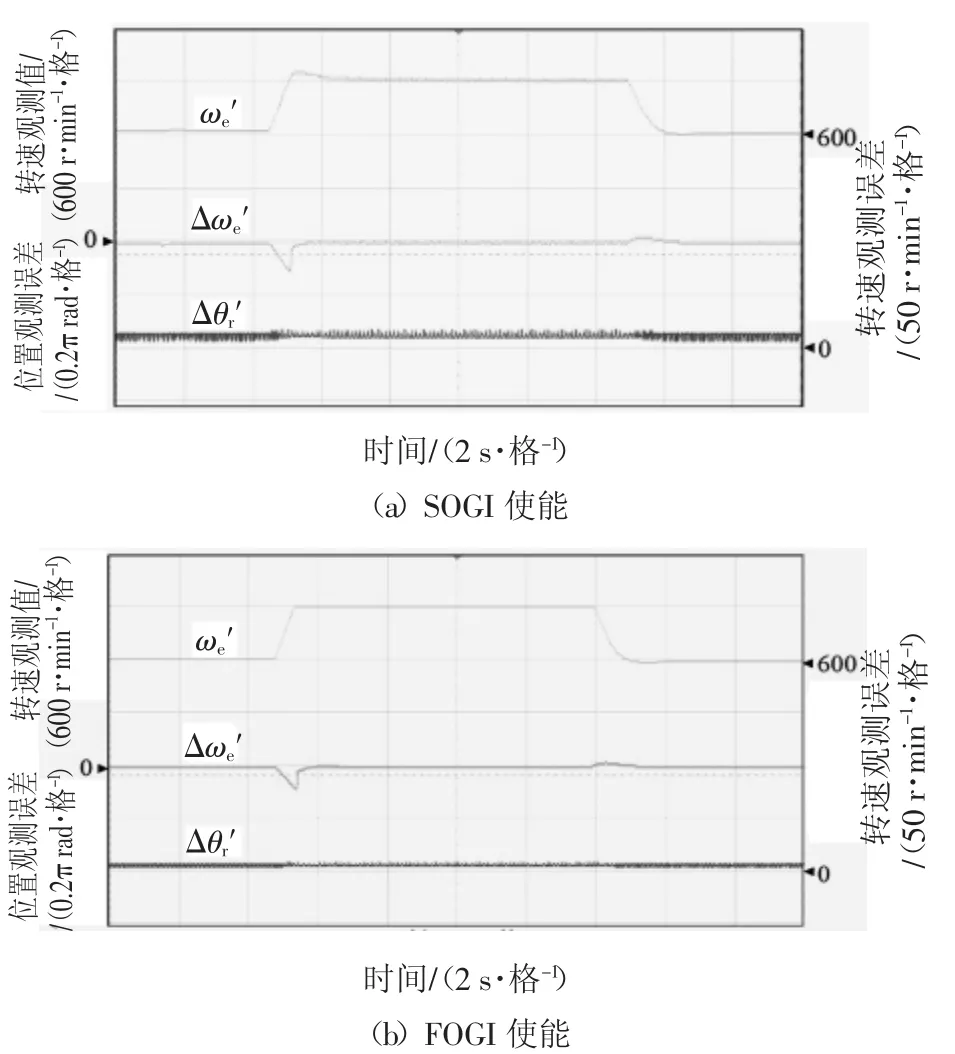
图15 加减速实验波形Fig.15 Experimental waveforms with speed variation

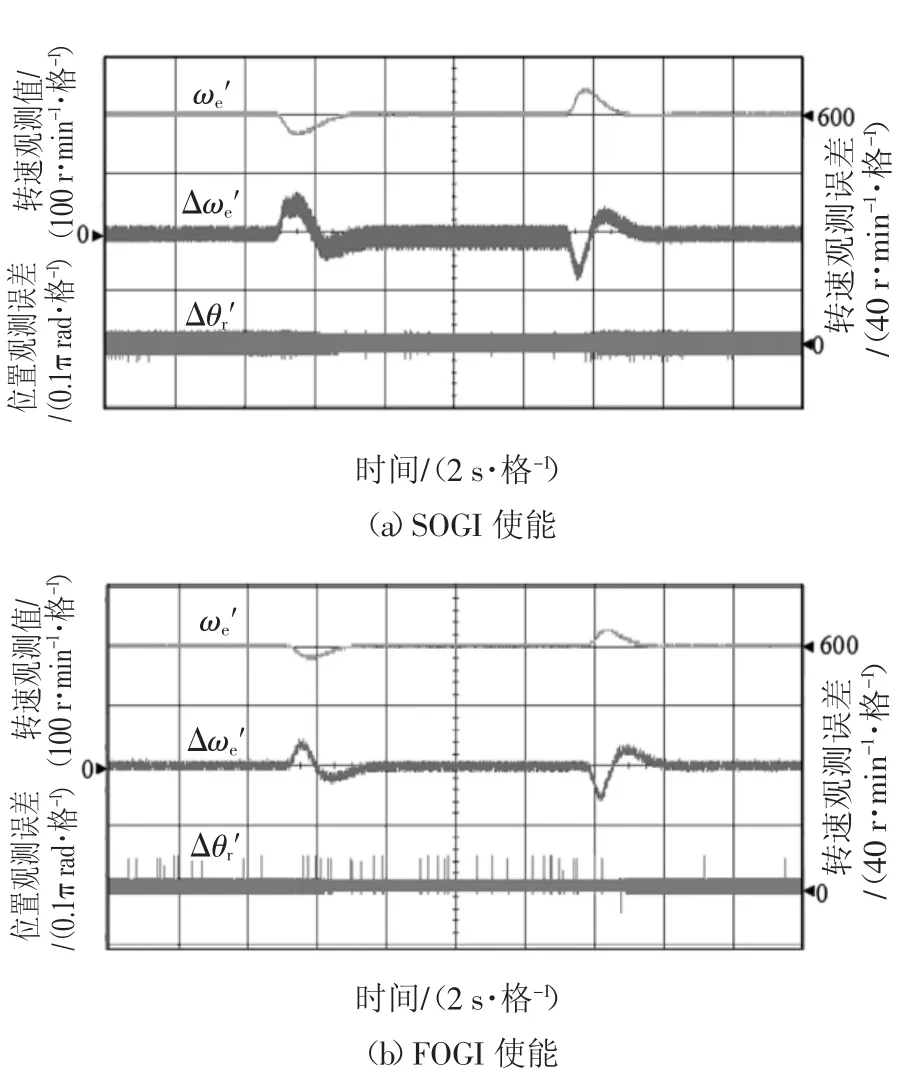
图16 加卸载实验波形Fig.16 Experimental waveforms with step load disturbance

4 结论

本文介绍了一种基于五阶广义积分器的IPMSM转子位置观测法，采用扩展反电动势模型的滑模观测器获取反电动势，通过锁相环计算转速、转子位置信息.考虑到逆变器非线性、磁场空间谐波、测量误差、积分初值不定等的影响，引入了五阶广义积分器抑制反电动势观测值中的直流分量和谐波误差，进而滤除转子位置信息中的谐波分量.仿真和实验结果证明：根据实际情况对五阶广义积分器进行合理的参数设置后，该方法能够有效抑制中转子位置观测中的谐波脉动误差，提高无传感器系统控制精度；在转速突变、负载加卸等动态过程中，五阶广义积分器都能呈现出比传统二阶广义积分器更好的控制效果.