基于凸轮机构驱动的无级变速器设计与仿真
马秋成,肖江,张魁,孙宁,陈强,尹谷林
(湘潭大学 机械工程学院,湖南 湘潭 411105)
无级变速器(Continuously Variable Transmission,CVT)是指可以连续获得变速范围内任何传动比的变速系统[1].近年来,随着车辆油耗及排放法规的日趋严苛,无级变速器得到了迅猛的普及和发展[2-3].相比于有级变速系统,无级变速器优点在于结构简单、传动效率高、能耗低[4-6],可获得传动系与发动机工况的最佳匹配,提高燃油的经济性并降低排放[7-8].
现有无级变速方式大多数是通过改变主、从动轮传动半径比来实现,如:金原茂[9]研制了一种金属带式无级变速器,该无级变速器主要由驱动带轮、从动带轮以及金属带组成,驱动带轮和从动带轮分别包括成对的固定滑轮和移动滑轮,通过调整移动滑轮位置,改变驱动带轮与从动带轮的槽宽进而改变与金属带的接触半径来变更传动速比,实现无级变速;金红光[10]研制出了一种液轮式无级变速器,该无级变速器包括主动轮、从动轮以及将主、从传动轮连接的传动带等部件,其中的主、从传动轮由具有封闭内腔的外壳以及填充其中的流体组成,外壳通过沿轴向的拉伸或压缩来改变传动轮的直径,实现无级变速,从本质上来说,该变速方式也是通过改变主、从传动半径来实现无级变速的.对于通过改变主、从传动半径比值的无级变速方式,由于其最大与最小半径是有限的,其最大速比也是有限的,因此变速范围较小,且因采用摩擦方式传递转矩,其传动损失较高,效率较低,直接影响到CVT 的应用效能[11-12].
此外,还有其他无级变速实现方式,如小林庸浩[13]研制出了一种采用调节旋转半径方法的无级变速器,其核心为旋转半径调节机构,通过自由调节旋转部的旋转半径改变传动比,实现无级变速.F·A·托马西[14]研制出了一种具有围绕主动轴线成角度布置的多个牵引行星轮的无级变速器,每个牵引行星轮具有可倾斜的旋转轴线,每个倾斜的位置构成不同的传动比,从而实现无级变速的目的.上述机构都能较好地实现无级变速,但存在结构复杂、变速范围窄、最大传动比小等不足.
针对上述问题,本文提出一种基于凸轮机构驱动的无级变速器.该无级变速器利用杠杆原理,通过调整杠杆支点位置,改变力臂,从而调节从动件的旋转速度,实现无级变速.基于凸轮机构驱动的无级变速器其优点在于结构紧凑、可靠性高、制造成本低,可获得较大的调速范围和大的传动比.本文通过对凸轮以及摆臂轮廓曲线的设计和仿真,分析不同传动比状态下摇臂的转速-时间曲线,验证该无级变速器运动的连续性以及工作输出的平稳性,较大程度上克服了前述无级变速器存在的不足.
1 变速原理
基于凸轮机构驱动的无级变速器,其结构简图如图1 所示,主要包括传动机构、变速机构、复位机构.传动机构主要由输入轴、凸轮、摆臂、摇臂、单向离合器以及输出轴组成.工作时(传动比固定,调速盘静止),输入轴驱动凸轮旋转,凸轮推动摆臂以中间轴为支点摆动,摆臂外轮廓曲线带动摇臂运动,摇臂与输出轴采用单向离合器连接,单向离合器将摇臂的往复摇摆运动,转化为单向旋转运动传递给输出轴,实现运动单向旋转输出.为实现运动连续输出,传动机构共有4 组,相对于调速盘中心对称布置,如图2 所示.4 组凸轮成一定相位角布置在输入轴上,单个凸轮上有四段推程曲线,4 组凸轮运动时,交替推动摆臂,使得传动机构在运动时,至少有一组凸轮处于推程状态,最终实现输出轴单向连续运动输出.
变速机构主要由调速杆和调速盘组成,调速盘通过滚动轴承安装在输入轴上,两者独立运动.摆臂通过中间轴安装在调速盘上,并可绕中间轴支点O2转动.当无级变速器变速时,调速杆带动调速盘旋转,摆臂支点O2随调速盘旋转而位置变化,并改变摆臂支点O2到摆臂与摇臂接触点B 之间的距离O2B,从而改变摆臂与摇臂接触点B 的运动速度,并通过摇臂改变输出轴的转速,实现变速运动.当调速盘顺时针旋转时,O2到接触点B 之间的距离增大,摇臂的角位移增大,传动机构输出较高的转速;当调速盘逆时针旋转时,O2到接触点B 之间距离减小,摇臂的角位移减小,传动机构输出较低的转速;当调速盘逆时针旋转到摆臂休止弧段(下端圆弧)与摇臂接触时,摇臂的角位移为0,此时从动件摇臂的输出转速为0,传动比趋近于无穷大.

图1 无级变速器结构简图Fig.1 Structure diagram of CVT

图2 传动机构Fig.2 Transmission mechanism
该机构的运动传递是通过输入轴带动凸轮、凸轮推动摆臂、摆臂推动摇臂来实现的,为保证运动连续输出,在凸轮的回程段,需要对摆臂和摇臂设计复位机构.复位机构包括摆臂复位机构和摇臂复位机构,分别实现摆臂滚轮与凸轮轮廓曲线、摇臂滚轮与摆臂轮廓曲线始终保持接触.摆臂复位机构主要由弹簧补偿器、复位索、支架、滑轮等组成,如图3 所示.支架固定在调速盘上,复位索通过弹簧补偿器分别与调速盘同侧的两组摆臂相连接,同时,两组摆臂对应的凸轮错位一定角度,使当凸轮1 处于推程状态时,凸轮2 处于回程状态,保证在一个推程时间内,复位索两端的拉伸距离和回缩距离相等.由于凸轮推程曲线和回程曲线不完全对称,只是回程距离和推程距离相等,因此复位机构在复位过程中,复位索两端会产生位移差.该位移差通过弹簧补偿器内的弹簧拉伸和压缩来补偿,使摆臂与凸轮始终保持接触.摇臂复位机构与摆臂复位机构原理相同.
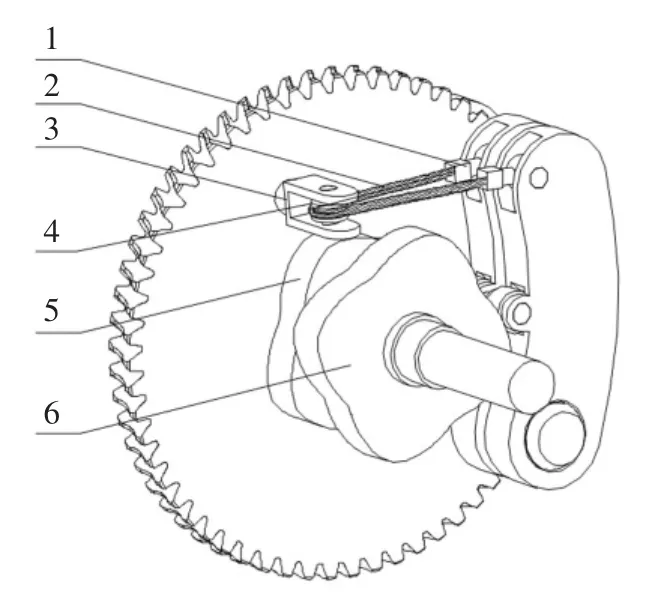
图3 摆臂复位机构Fig.3 Swing arm reset mechanism
2 传动比分析
传动比是指变速机构输入角速度与输出角速度的比值,是反映变速装置变速大小的一个重要参数,因此,在无级变速器设计前,需要对无级变速器的传动比特性进行分析.
根据前述变速原理,本无级变速器的单组传动机构运动简图如图4 所示,其总的传动比为:

式中:i12、i23分别为凸轮-摆臂、摆臂-摇臂之间的传动比.
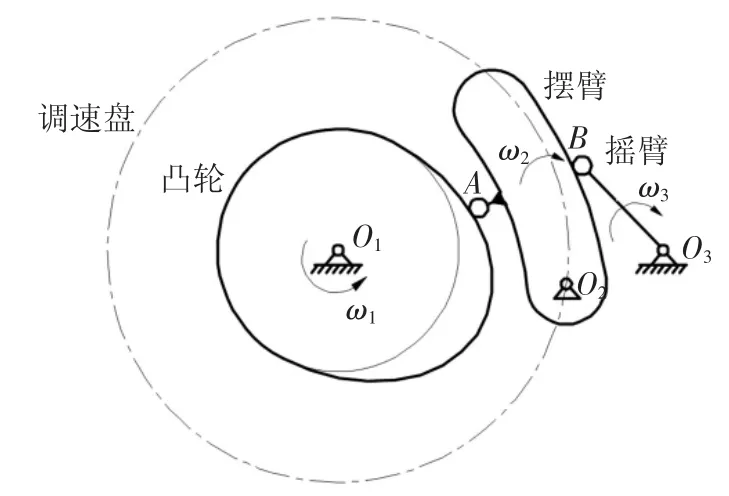
图4 传动机构运动简图Fig.4 Schematic diagram of transmission mechanism
2.1 凸轮-摆臂机构传动比计算
凸轮-摆臂机构为摆动从动件凸轮机构,其机构运动简图如图5 所示.图5 所示位置为推程状态下的一个位置,摆臂的瞬时速度为v2,凸轮转动的角速度为ω1.根据压力角定义,可作出凸轮机构的压力角α1,由瞬心知识可知,P1为凸轮和从动件摆臂的速度瞬心,故有:v2=,由此可得凸轮-摆臂的传动比为:
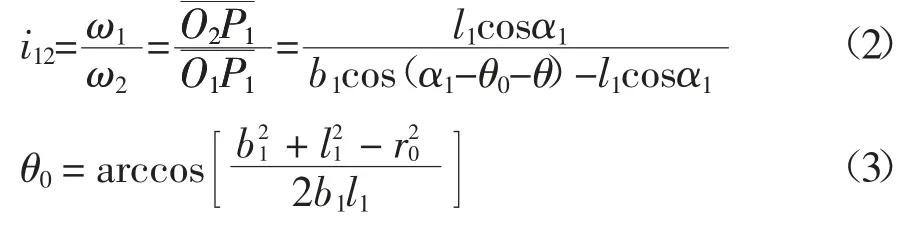
式中:l1为凸轮-摆臂机构中摆臂的传动半径;b1为凸轮与摆臂的中心距;r0为凸轮基圆半径;θ 为摆臂的运动摆角;α1为凸轮-摆臂机构压力角.
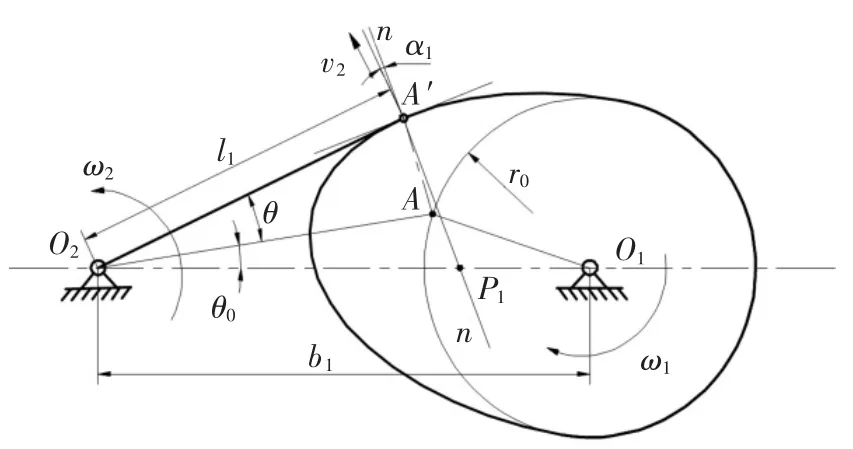
图5 凸轮-摆臂机构运动简图Fig.5 Motion diagram of cam-swing arm mechanism
2.2 摆臂-摇臂机构传动比计算
摆臂-摇臂机构也可看作摆动从动件凸轮机构,摆臂看作是凸轮,其机构运动简图如图6 所示.用前述凸轮-摆臂机构的传动比推导方法,可推出摆臂-摇臂机构传动比为:

式中:l2为摆臂-摇臂机构中摇臂的传动半径;b2为摆臂与摇臂的中心距;R 为摆臂轮廓曲线推程的起始点到旋转中心的距离;φ 为摇臂的运动摆角;α2为摆臂-摇臂机构压力角.
根据图6,当调速盘逆时针旋转到摆臂休止弧段(下端圆弧)与摇臂接触时,摆臂与摇臂的瞬心P2与摆臂旋转中心O2重合,O2P2=0,由式(4)可知,此时传动比i23接近无穷大,这是本文无级变速器传动比大的理论依据.
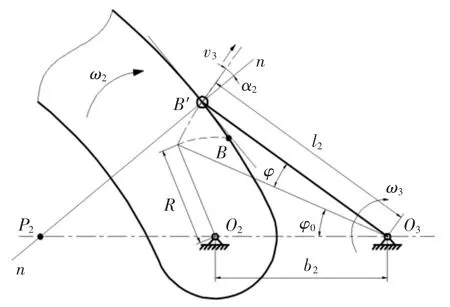
图6 摆臂-摇臂机构运动简图Fig.6 Motion diagram of swing arm-rocker arm mechanism
2.3 凸轮机构总传动比分析
将i12、i23代入式(1)可以得到无级变速器总的传动比为:

由式(9)可以看出,当调速盘处于某一调速位置时,b1、b2、l1、l2、r0、R 均为定值,此时摇臂的输出转速只与α1、α2、θ、φ 有关,即瞬时传动比的变化主要受α1、α2、θ、φ 的影响.而θ、φ与摆臂和摇臂的运动规律有关,α1(α2)与凸轮(摆臂)轮廓曲线在接触点A(B)处的曲率有关,即压力角大小与轮廓曲线形状有关.因此,要实现摇臂输出速度平稳,需要对凸轮(摆臂)轮廓曲线进行设计,使得压力角α1(α2)按一定规律变化,补偿θ、φ值变化对摇臂输出转速的影响,获得摇臂转速的平稳输出.
3 摆臂轮廓曲线设计
无级变速器是指可在变速范围内连续获得任何传动比的变速系统.为使任意传动比条件下,无级变速器都具有平稳的转速输出,摆臂轮廓曲线设计时,需先求得不同传动比时的摆臂曲线,然后对其优化拟合,最终得到整体轮廓曲线.
具体设计方法为:从摆臂-摇臂机构输出转速为零,即传动比无穷大时开始,调速盘逐次顺时针旋转δ 角度,如图7 所示,调速盘旋转n 次后,摇臂与摆臂轮廓曲线的初始接触位置由B 到达点B′,记δn为调速角,δn=nδ,n 为调速盘递增角度的次数,记传动比无穷大时,n=0;为使摆臂-摇臂机构的传动比与调速角成线性变化,实现无级变速,在摆臂轮廓曲线设计之前,需将调速盘的旋转角与传动比关联,在不同调速角时得到的摆臂曲线即为不同传动比时获得的摆臂轮廓曲线,构建线性关联函数:i23=f(δn).
在整体摆臂轮廓曲线设计时,先求出δ0时摆臂曲线,随后依次求出δ1、δ2、…、δn时摆臂轮廓曲线,最后将不同传动比时的摆臂轮廓曲线拟合,得到整体摆臂轮廓曲线.
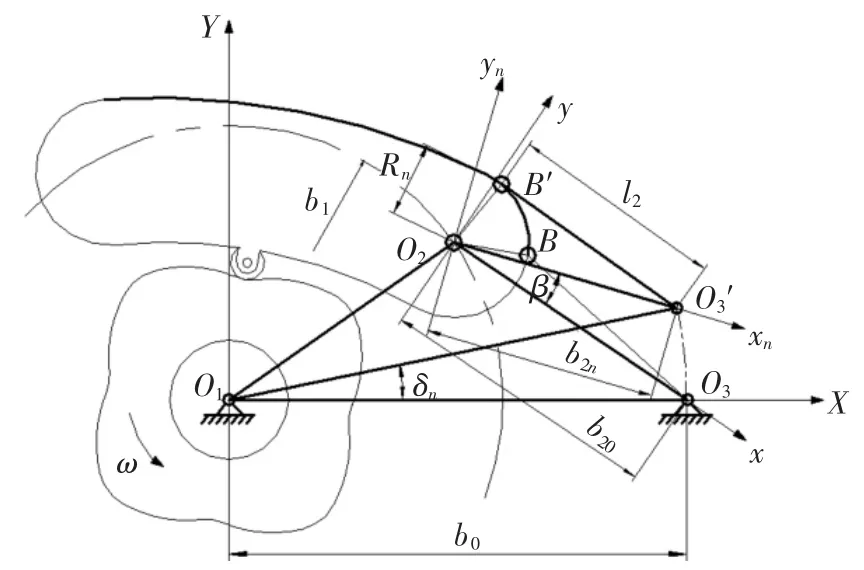
图7 调速角δn 时摆臂位置Fig.7 Position of swing arm when speed regulating angle δn
3.1 任意传动比时摆臂曲线设计
以摆臂旋转中心和摇臂旋转中心连线为X 轴,设定当n=0 时坐标系为原始坐标系O2xy,图8 为调速盘递增n 次后,摆臂-摇臂相对位置,此时坐标系为O2xnyn.点B 为摆臂轮廓上推程的起始点,当摆臂转过θ 角时,从动件接触点从初始位置B 旋转φ 角后到达点B′.根据反转法原理,可以得到摆臂轮廓线上点B′,在O2xnyn坐标系中的方程为:

其中:φn为调速盘旋转第n 次时的摆臂初始角,其值为φn=];Rn为调速盘旋转第n次时摆臂的基圆半径,Rn的值通过作图法得到,其长度为调速角δn时,摇臂滚轮与δn-1时摆臂轮廓曲线的交点B 到O2的距离,R0为初始设定值,其大小为摆臂休止弧段圆弧半径,为方便后续曲线拟合优化,Rn的取值一般略小于测量值;l2为摇臂对摆臂的传动半径;b2n为调速盘旋转第n 次后,摆臂与摇臂中心距.由图7 可得到b2n的关系式为:
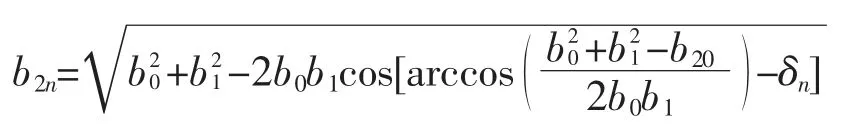
式中:b0为凸轮与摇臂中心距;b1为凸轮与摆臂中心距;b20为摆臂与摇臂起始中心距.
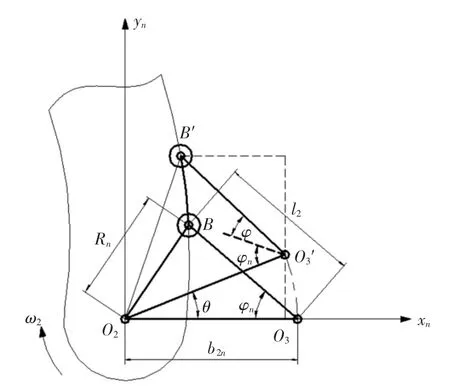
图8 调速角δn 时摆臂曲线设计Fig.8 Curve design of swing arm when the speed regulation angle δn
调速盘旋转第n 次后,如图7 所示,直角坐标系O2xy 旋转β 角度后变为O2xnyn,旋转角β 值为:
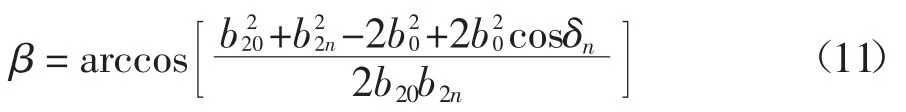
进行坐标变换,可得到任意传动比时的摆臂轮廓曲线,在初始坐标O2xy(i=∞)中的投影坐标方程为:

3.2 传动平稳性仿真优化
本节以一组摆臂参数为例,用式(12)计算不同传动比对应的摆臂曲线,并对所得曲线进行拟合得到摆臂轮廓曲线.用NX10 软件对摆臂-摇臂传动过程进行运动学仿真,验证上述设计方法得到的摆臂轮廓曲线,是否能在任意传动比时无级变速器都具有平稳的运动输出.
基于式(4),一组摆臂-摇臂机构设计参数为:b20=110 mm;l2=100 mm;b0=185 mm;b1=110 mm;R0=30 mm;摆臂-摇臂最小传动比i23=0.5,摆臂最大摆角θ=10°;i23与δn关联函数,i23=50/δn,即调速盘最大调速角δn=100°时,i23为最小值,且最小值为0.5;此外,定义摆臂轮廊曲线设计时的单次旋转角度δ=5°.基于上述设计参数,在NX10 中拟合建立摆臂轮廓曲线,并建立如图9 所示的运动学仿真模型.仿真时,摇臂与摆臂之间的运行副选用NX10 仿真模块中的线在线上副,使摆臂滚轮与摆臂曲线始终保持接触,仿真时摆臂输入ω2=5 r/s,仿真时间为0.005 s,即当摆臂摆角θ=10°时,摆臂达到极限位置.
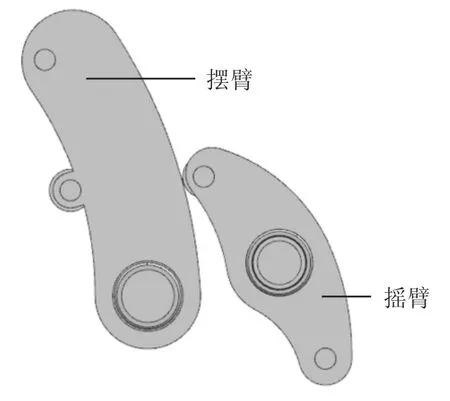
图9 摆臂-摇臂仿真模型Fig.9 Simulation model of swing arm and rocker arm
不同调速角时摇臂输出转速的仿真结果如表1所示.

表1 摆臂转速恒定时摇臂输出转速Tab.1 Output speed of rocker arm when the speed of swing arm is constant
由表1 可以看出,在某固定调速角时,摇臂输出转速是变化的,并呈线性增长趋势,说明传动过程不平稳.为定量评价无级变速器传动的平稳性,以波动率ε 为评价指标:

式中:ωmax为一个周期内速度波动的最大值;ωmin为一个周期内速度波动的最小值;为一个周期内速度平均值.
因摇臂输出端转速随时间线性增长,因此有:

式中:ω3(t0)为摇臂起始时间的旋转速度;ω3(t1)为摇臂终止时间的旋转速度.波动率ε 与调速角的关系曲线如图10 所示.
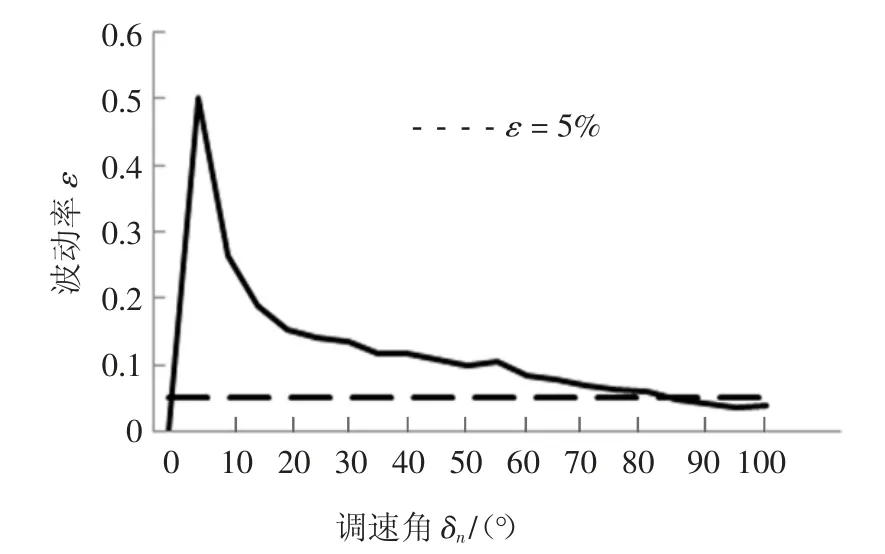
图10 不同δn 时摇臂输出的波动率Fig.10 Fluctuation rate of rocker arm output under different δn
从图10 可看出,当调速角比较小时,波动率ε较大,传动平稳性差.随着调速角的增大,波动率ε整体呈递减的趋势,当δn大于80°时,波动率ε 小于5%,此时传动比i23的范围为0.58~0.72,由于变速范围较窄,工程应用价值不高.
为降低输出转速的波动率,提高运动的平稳性,根据摇臂输出端转速随时间线性增长的变化规律,拟通过控制摆臂转速,使其按一定规律变化,实现对输出速度的反向补偿,达到减小波动率的目的.

根据摆臂-摇臂机构传动比定义,可得到摇臂转速变化规律为:

联合式(15)(16)可得:

式中:i23(t0)、i23(t1)分别为摆臂-摇臂机构的起始传动比和终止传动比;ω2(t0)为摆臂推程起始转速;ω2(t1)为摆臂推程终止转速;ω3(t0)和ω3(t1)分别为ω2为恒定值时,摇臂起始旋转速度与摇臂终止旋转速度.

为方便运算,ω2(t)选取一次规律函数,可推算出摆臂转速规律方程为:式中:θ 为摆臂最大位移摆角;g 为摆臂-摇臂机构推程过程中,终止旋转速度与起始旋转速度的比值.
根据表1 速度变化规律,可得图11 所示的δn-g曲线图.从图11 可以看出,g 值大小主要集中在0.8~1.0 内;通过仿真分析,发现当g 取值越接近0.915时,摇臂平稳输出的调速范围越大,因此选取g 值为0.915.根据无级变速器选取的设计参数θ=10°、t=0.005 s、ω2=5 r/s,可得摇臂运动规律为:

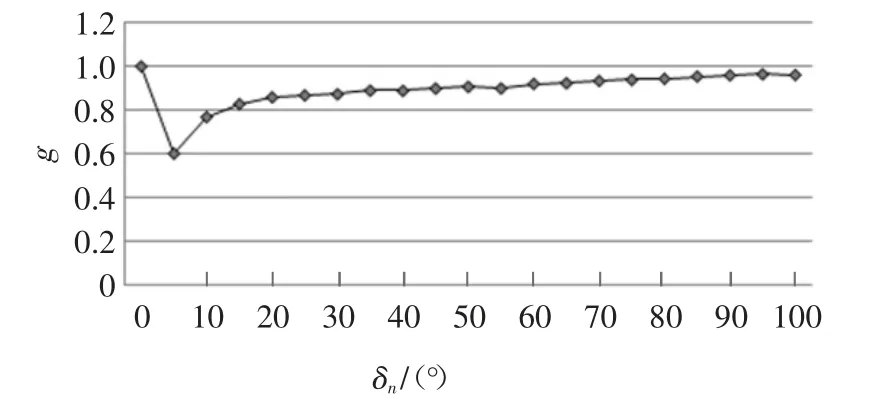
图11 δn-g 曲线图Fig.11 δn-g relation curve
4 凸轮组件设计
4.1 凸轮曲线设计
以凸轮旋转中心和摆臂旋转中心连线为X 轴建立直角坐标系O1XY,如图12 所示.B 点为凸轮轮廓上推程的起点,利用反转法原理,凸轮转过γ 角时,B运动到B′点,B′点即为凸轮轮廓曲线上的点.

图12 凸轮轮廓曲线设计图Fig.12 Cam profile design drawing
建立B 点封闭矢量方程:

投影得凸轮轮廓线B 点坐标:
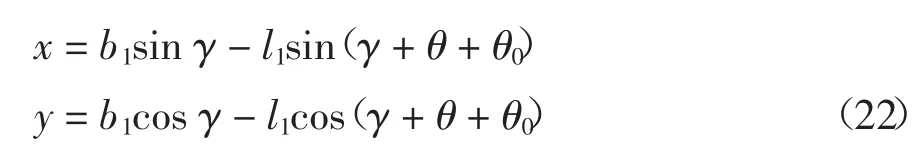
式中:l1为凸轮-摆臂机构中摆臂的传动半径;b1为凸轮与摆臂的中心距;θ0为摆臂的运动摆角;γ 为凸轮推程角.θ0由式(3)可得.
4.2 凸轮组设计
基于3.2 节摆臂仿真实例的参数,对凸轮轮廓曲线进行设计,根据式(2)得到一组凸轮-摆臂设计参数为:r0=50 mm;l1=80 mm;b1=110 mm;凸轮-摆臂最小传动比为i12=3,在NX10 中建模,可得到凸轮轮廓曲线.
图13 为摆臂的角位移曲线图,图中0~1 为提速阶段,摆臂转速从0 增加到5 r/s;1~2 为凸轮有效推程阶段,此时摇臂获得平稳输出,摆臂运动规律为ω2(t)=5-85t;2~3 为降速阶段,摆臂转速下降到0;3~4 为回程阶段.
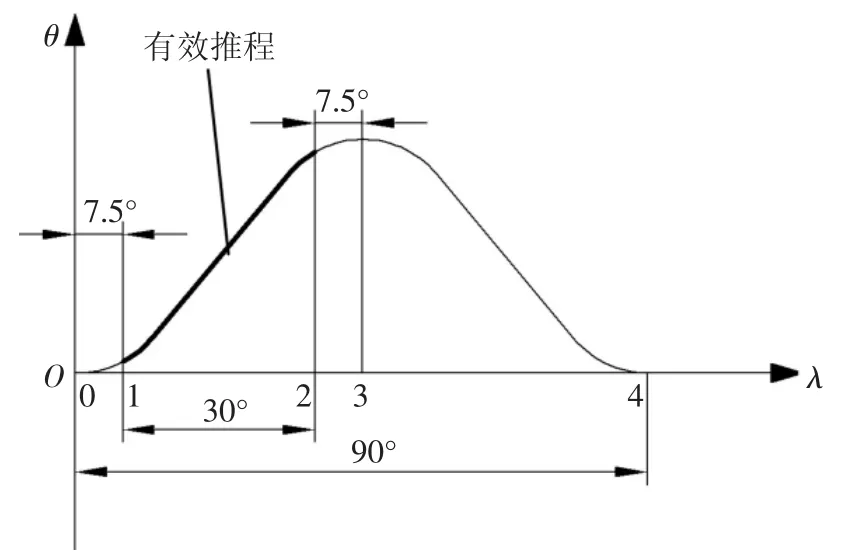
图13 单组摆臂角位移曲线Fig.13 Single swing arm angle displacement curve
由图13 可知,单组凸轮只有1/3 的时间处于有效推程状态,因此,为使机构获得连续输出,将4 组凸轮均匀错开,错位角为22.5°,考虑到机构复位,凸轮1 处于推程状态时凸轮2 需处于回程状态;凸轮组布置时,将第1 组凸轮与第2 组凸轮错位45°,第2 组凸轮与第3 组凸轮错位-22.5°,第3 组凸轮与第4 组凸轮错位45°.
4 组凸轮错位后,4 组摆臂的叠加角位移曲线如图14 所示.由图14 可知,在凸轮组传动过程中,其中1/2 时间有两组凸轮始终处于有效推程状态,剩余1/2 时间有一组凸轮处于有效推程状态,这种设计可以保证在机构运动过程中,至少有一组凸轮处于有效推程状态,实现运动连续输出.

图14 摆臂角位移曲线Fig.14 Swing arm angle displacement curve
5 传动机构运动学仿真
为验证本文无级变速器在任意传动比状态下都具有连续平稳的运动输出,本节利用NX10 软件对上述实例进行运动学仿真,传动机构三维仿真模型如图15 所示.输入轴输入转速ω1=15 r/s,仿真时间为0.02 s.
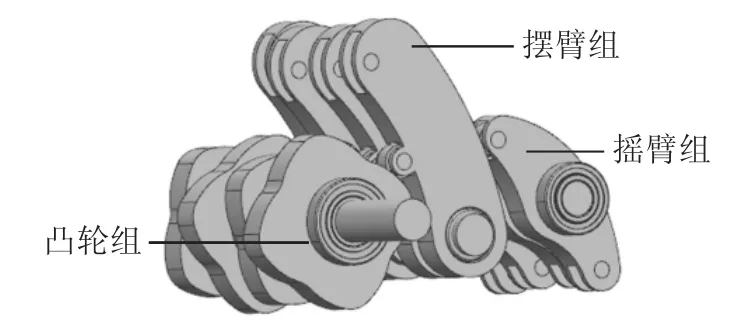
图15 传动机构仿真模型Fig.15 Simulation model of transmission mechanism
将NX10 的仿真结果导入Origin 中,绘制出4组传动机构摇臂输出角位移-时间曲线图,如图16所示.由图16 可以看出,4 组摇臂曲线先后重叠,证明传动机构在运动过程中,至少有一组摇臂处于推程状态,无级变速器可实现运动连续输出.

图16 摇臂输出角位移-时间曲线图Fig.16 Curves of rocker arm output angular displacement-time
提取NX10 仿真结果中的摇臂输出转速,得到不同调速角时,摇臂的最大转速、最小转速和平均转速如表2 所示.根据表2 中的摇臂平均转速,得到摇臂平均转速与调速角的关系图,如图17 所示.由图17 可以看出,摇臂的平均转速与无级变速器调速角δn成线性关系,且随着调速角增大平均转速线性增大.说明本文所提出的无级变速器,可通过改变调速角的大小调节输出转速,实现无级变速.
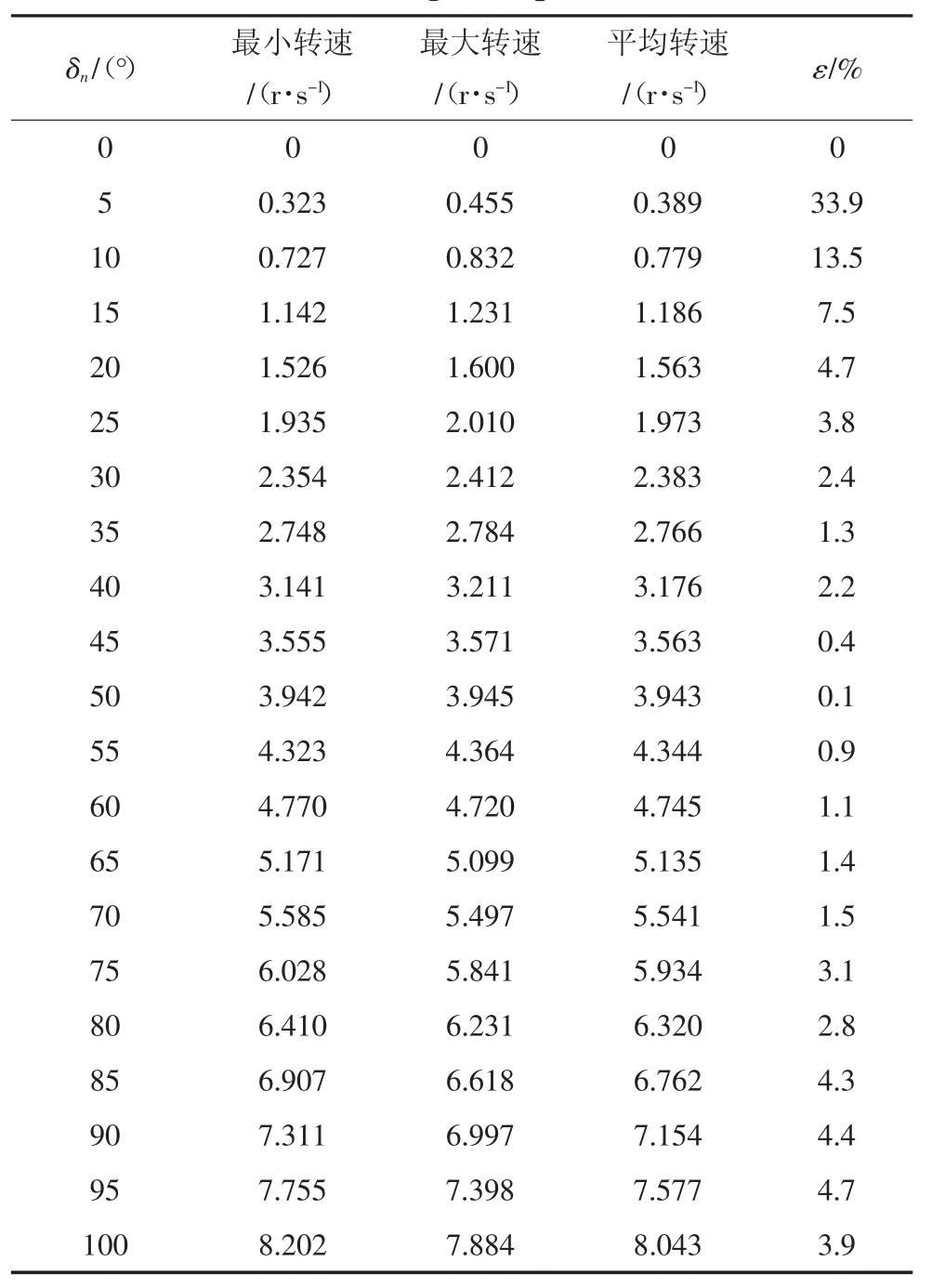
表2 摆臂转速优化后摇臂输出转速Tab.2 Output speed of rocker arm after optimization of swing arm speed
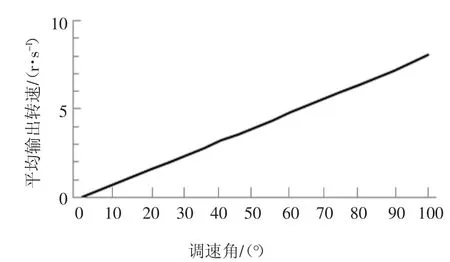
图17 不同调速角时摇臂平均输出转速Fig.17 Average output speed of rocker arm at different speed control angles
根据表2 中的波动率ε,得到无级变速器δn-ε曲线如图18 所示.由图18 可以看出,当δn≥20°时,输出转速的波动率ε 均小于5%,可实现摇臂转速平稳输出.
综上所述,本文无级变速器的总传动比在一定调速角范围内,可实现运动连续平稳输出.
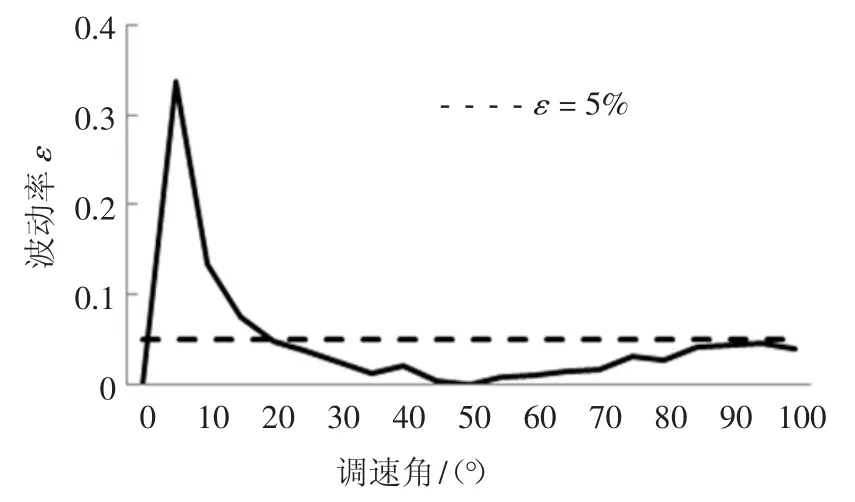
图18 摆臂转速优化后无级变速器输出波动率Fig.18 Output fluctuation rate of CVT after optimization of swing arm speed
6 结论
1)本文提出了一种基于凸轮机构驱动的无级变速器,该无级变速器通过变速装置,调整中间杠杆支点位置,改变力臂,从而调节从动件旋转速度,可获得较宽的变速范围和较大的传动比.并对无级变速器传动比进行了分析,从原理上验证了该机构无级变速的可行性.
2)为降低输出转速的波动率,根据摇臂输出端转速随时间线性增长的变化规律,通过控制摆臂转速,使其按一定规律变化,实现了对输出速度的反向补偿,提高了运动输出的平稳性.
3)为使无级变速器输出转速稳定,利用反转法对摆臂轮廓曲线以及凸轮轮廓曲线进行设计,并将凸轮组中凸轮均匀错开22.5°,保证机构在运行的过程中,至少有一组凸轮处于有效推程状态.最后用NX10 软件对无级变速器整体进行了运动学仿真,验证了该无级变速器可实现无级变速,并在一定调速角范围内实现运动的连续平稳输出.

