铁基超导涡旋演生马约拉纳零能模*

孔令元 丁洪3)†

1) (中国科学院物理研究所， 北京凝聚态物理国家研究中心， 北京 100190)2) (中国科学院大学物理科学学院， 北京 100049)3) (中国科学院大学， 中国科学院拓扑量子计算卓越中心， 北京 100049)(2020 年5 月12日收到; 2020 年5 月30日收到修改稿)

作为马约拉纳零能模(MZM)的一种全新载体， 具有拓扑能带结构的铁基超导块材——拓扑铁基超导体——近年来引起了学术界的广泛关注. 由于同时具备单一材料、高温超导、强电子关联、拓扑能带等特质，拓扑铁基超导体成功规避了本征拓扑超导体和近邻异质结体系在实现MZM上的困难， 为马约拉纳物理开辟了自赋性拓扑超导的新方向. 时至今日， 人们已经在多种拓扑铁基超导体的磁通涡旋中测量到了纯净的MZM. 实验发现， 铁基超导体系中演生的涡旋MZM信号明确、物理清晰， 具有很好的应用前景. 拓扑铁基超导体有望成长为研究马约拉纳物理和制备拓扑量子比特最重要的材料体系之一. 本文以Fe(Te，Se)为主要对象详细介绍了铁基超导马约拉纳载体的思想起源和研究进展. 在阐明Fe(Te，Se)拓扑能带结构和零能涡旋束缚态基本实验事实的基础上， 本文将逻辑清晰地系统总结铁基超导涡旋演生MZM的主要实验观测和基本物理行为; 借助波函数、准粒子中毒等实验， 解析Fe(Te，Se)单晶中的涡旋MZM演生机制; 结合现有马约拉纳理论， 深入探讨铁基超导体中的马约拉纳对称性和准粒子拓扑本质的实验测量. 最后， 本文采用“从量子物理到量子工程”的视角， 综合分析涡旋MZM在真实材料和实际实验中的鲁棒性， 为未来潜在的工程应用提供有益指导. 本文以物理原理为线， 注重理论与实验结合， 旨在搭建经典马约拉纳理论与新兴拓扑铁基超导体系之间的桥梁， 帮助读者理解铁基超导涡旋中演生的MZM.

1 引 言

凝聚态物理系统中的马约拉纳零能模(MZM)是束缚在超导体缺陷上的零能拓扑准粒子[1-5]， 它具有三个基本性质: 其一， 具有马约拉纳(Majorana)对称性. 这要求空穴和粒子成分等价混合， MZM的产生/湮灭算符在共轭变化下保持不变， 准粒子呈现电中性. 与标准模型中“反粒子是其自身”的Majorana费米子十分类似， 只有孤立的MZM才能稳定存在， 两个MZM相遇会融合成一个普通的费米子; 其二， 具有拓扑非平庸性， MZM是等效拓扑超导体的边界态， 它的出现伴随着非平庸的全局拓扑不变量; 其三， 具有非阿贝尔任意子性质(non-Abelian anyon). MZM是费米子的“一半”，它的量子维度为. MZM在交换操作下遵守非阿贝尔任意子统计规律， 编织MZM可以构筑量子比特， 实现容错拓扑量子计算[6-9]， 鉴于此， 最近十年来MZM基本物理及潜在应用的研究是凝聚态物理和量子物理领域最前沿和最活跃的方向之一.

超导电性具有本征的粒子-空穴冗余， 超导准粒子是空穴和电子的量子叠加态， 这一性质为MZM的出现提供了便利. 人们可以通过妥善设计超导体， 使得MZM以拓扑准粒子激发的形式出现在超导缺陷上. 由于受到Majorana对称性和超导体粒子-空穴对称性的双重限制， 超导体中的MZM一定是零能准粒子. 超导磁通涡旋是第二类超导体在磁场下自发形成的量子化拓扑缺陷[10-12]. 涡旋中心的超导序参量为零， 随着远离涡旋中心超导序参量恢复到正常值. 同时超导相位随着以涡旋中心定义的极角变化而变化， 超导相位变化与极角变化的比值可以定义超导涡旋的涡旋数(vorticity). 超导磁通涡旋可以看作是超导准粒子的量子阱. 在这种量子阱中， 超导准粒子以涡旋束缚态的形式存在， 其行为可以通过求解涡旋Bogoliubov-de Genne (BdG)方程获得:

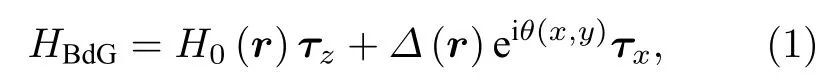
在超导磁通涡旋中创造MZM需要满足两个必要条件: 其一， 产生零能模， 这需要在BdG方程中额外引入大小为π的奇数倍的几何相位， 使得涡旋束缚态的能级满足 En≈ nΔ2/EF; 其二， 稳定单个零能模， 这需要通过某种方式破除自旋简并. 在20年前的世纪之交， 人们意识到手性p波超导体(px+ ipy)的超导准粒子携带大小为π的本征几何相位， 这可以抵消零点能导致的反周期性涡旋边界条件， 使涡旋束缚态存在零能解[16-20]. 拓扑理论分析进一步证明， 弱耦合手性p波超导体是本征拓扑超导体， 它的准粒子谱具有非平庸的拓扑不变量[16].理论证明， 无自旋手性p波超导体的常规量子化磁通涡旋(φ = h/(2e))中存在稳定的单个MZM. 而有自旋手性p波超导体的常规磁通涡旋中存在两个MZM， 它们融合成一个普通费米子. 理论研究进一步发现， 有自旋手性p波超导体中的自旋自由度可以通过半整数磁通涡旋(φ = h/(4e))的方法破除. 在半整数磁通涡旋中， 涡旋只与一个自旋分量耦合， 涡旋中心存在稳定的单个MZM[17，18]. 手性p波超导体的思想可以追溯到5/2分数量子霍尔效应[21]. 5/2分数量子霍尔效应的Paffian态(也被称为Moore-Read态)将强磁场中的自旋极化电子映射为零场下发生无自旋手性p波配对的复合费米子， Majorana模式出现在其边界、涡旋等拓扑缺陷上[22]. 尽管本征拓扑超导体中的MZM理论十分清晰， 但是手性p波超导体和半整数磁通涡旋在实验上都很难实现[23]， 这极大地限制了MZM的研究.

这一僵局直到2008年Fu-Kane模型[24]问世才得以打破. Fu-Kane模型研究了二维无简并超导狄拉克(Dirac)表面态的准粒子行为， 开创性地证明s波超导配对的Dirac表面态具有和无自旋手性p波超导体等价的低能超导准粒子谱， MZM可以存在于s波超导体/拓扑绝缘体异质结界面的超导磁通涡旋中. Fu-Kane哈密顿量为

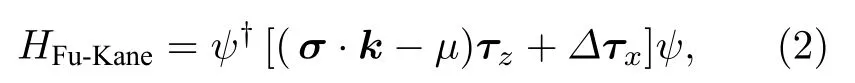
这恰恰描写了各向同性能带发生无自旋手性p波配对. 因此其超导准粒子谱与无自旋手性p波超导体等价， 稳定的单个MZM存在于Fu-Kane模型的常规超导磁通涡旋中.

由于成功规避了p波超导电性的困难， Fu-Kane模型将Majorana物理从理论假想带入了实验现实， 开启了MZM研究的新时代. 在这一思想的启迪下， 近十年来理论物理学家们在凝聚态物理体系中设计了多种方案可以实现Majorana准粒子. 通过进一步实验测量， 人们也发现了诸多MZM存在的迹象. 这些凝聚态体系按照物理机理大致可以分为以下几类: 1)打开Zeeman能隙的Rashba纳米线[28-30]， 包括半导体纳米线[31-34]、Au纳米线[35-37];2)具有强交换相互作用的螺旋自旋链， 包括磁性原子链[38-41]、磁性碳纳米管[42]; 3) Yu-Shiba晶格上的手性拓扑超导[43-48]; 4)超导近邻反常量子霍尔效应[49-54]; 5) Fu-Kane 磁性边界态[24]， 包括一维系统末端的MZM[55]以及二维系统边界上的手性Majorana模[56，57]; 6) Fu-Kane 约瑟夫森结中的螺旋Majarana模[24，58]; 7) Fu-Kane 磁通涡旋中的MZM[24，59-62]. 然而这些体系都使用常规s波超导体作为衬底， 通过异质结合其他具有拓扑能带结构的材料来实现MZM. 受限于s波超导体临界温度低(Tc)、超导能隙小的特点， 这些体系中出现的MZM往往具有极小的拓扑能隙， 需要在极低实验温度(Texp＜ 100 mK)下进行测量. 这不仅增加了实验成本， 也使得MZM更易被平庸束缚态干扰， 妨碍了人们从实验上深入研究MZM的行为. 另外， 异质结结构带来了难以控制的无序和制造复杂性[63]. 这些问题让平庸机制带来的类Majorana信号在实验中难以被排除， 使得MZM的确切证实变得扑朔迷离[34，54].Majorana领域的新飞跃有待MZM材料载体的范式革新.

本文系统回顾了先前MZM载体的困难， 对它们进行逐条分析找出了对症方案(图1(a))， 这为探索更优的MZM载体材料提供了重要启示. 首先，稀有的p波超导电性难以实现. Fu-Kane模型用拓扑能带的自旋贝里(Berry)相位代替本征拓扑超导体的超导相位缠绕(phase winding)， 规避了本征p波超导体的困难. 因此， 新的MZM材料载体应同时具有拓扑能带结构和自身超导电性， 这往往需要多能带结构， 便于分别实现拓扑和超导性质. 第二， 极低温实验条件的困难. MZM是超导准粒子， 它的存活温度与超导临界温度正相关. 利用更高临界温度的超导体替换常规s波超导体作为超导衬底可以有效提高MZM的存活温度. 考虑到涡旋束缚态的存在条件， 新的MZM材料载体应该是全能隙(full gap)非常规超导体， 比如s±波超导[64-67]， nodeless-d波超导等[68-71]. 第三， 拓扑能隙过小导致MZM易被污染. 拓扑能隙是MZM与第一激发态之间的能级间隔. 在涡旋中拓扑能隙正比于Δ2/EF. 可见费米能越小， MZM的拓扑能隙就越大. 一般而言， 小的能带带宽(band width)有利于EF的减小， 这表明强电子-电子相互作用带来的能带重整化有利于实现涡旋MZM. 第四， 异质结引入的困难. 去除异质结最直接的方法是利用单一材料聚合上述所有性质. 综上可知， 潜在更优的MZM材料载体应该是具有拓扑非平庸能带结构的多能带强关联高温超导材料.

结合长期研究经验， 我们意识到铁基超导体是有力候选者之一. 首先， 铁基超导体[72，73]的低能电子态主要由Fe的t2g轨道(分别为dxz， dyz， dxy轨道)和硫族元素的p轨道构成. 铁基超导体在费米能级附近分别有三条空穴型能带出现在布里渊区中心， 两条电子型能带出现在布里渊区边角(图1(b)).这些能带穿过费米能级， 产生多费米面结构， 实验发现铁基超导体的费米面在Tc以下通常打开全能隙[74]. 尽管目前对铁基超导机理尚未达成共识， 但是已有大量理论和实验结果支持自旋涨落导致的s ±配对机制(图1(c))[74-80]. 其次， 理论计算和实验测量都表明铁基超导体具有较强的电子-电子关联[81]，这使得铁基超导体能带具有可观的有效质量重整化. 例如Fe(Te， Se)的质量重整化因子与铜氧化物超导体中的数值接近(约为7)， 是铁基超导家族中关联性最强的材料(图1(d)). 因此， Fe(Te， Se)体能带具有非常小的费米能 (约10 meV) (图1(e))[82]，这一现象也被角分辨光电子能谱(ARPES)实验观测到. 最后， 一些早期理论表明， 铁基超导体具有拓扑非平庸的能带结构[83，84]. 理论预言在单层FeSe/STO[85]、单层Fe(Te， Se)[86]、Fe(Te， Se)单晶[87]、具有As链夹层的CaFeAs2[88]等体系中存在拓扑非平庸的能带反转， 在适当的参数空间内存在Dirac表面态. 另外也有理论预言铁基超导体中的有序态可以改变电子结构[89-97]从而创造拓扑能带， 例如人们在BaFe2As2的SDW态[89-92]以及FeSe单晶的电子向列态[94-97]等电子有序体系中发现了拓扑能带的迹象. 最重要的是， 一些早期实验表明Fe(Te， Se)单晶能带极有可能是拓扑非平庸的[87，98，99]. 2014年， 通过使用常规ARPES和表面原位电子掺杂方法， 我们发现FeTe0.55Se0.45单晶的原始费米能级以上存在电子型能带[98]， 随后我们又通过变光子能量和偏振的ARPES技术， 观测到了体态能带反转的证据[87]. 同时， 一项早期的扫描隧道显微镜/谱(STM/S)实验发现FeTe0.55Se0.45单晶的间隙Fe原子上存在鲁棒的零能束缚态[99]，这些证据都暗示FeTe0.55Se0.45单晶具有拓扑非平庸的能带结构. 这些线索将我们的注意力吸引到FeTe0.55Se0.45单晶上， 启发我们通过后续实验在铁基超导体表面清晰地观测到了超导拓扑表面态[100，101]和涡旋MZM[102-106].

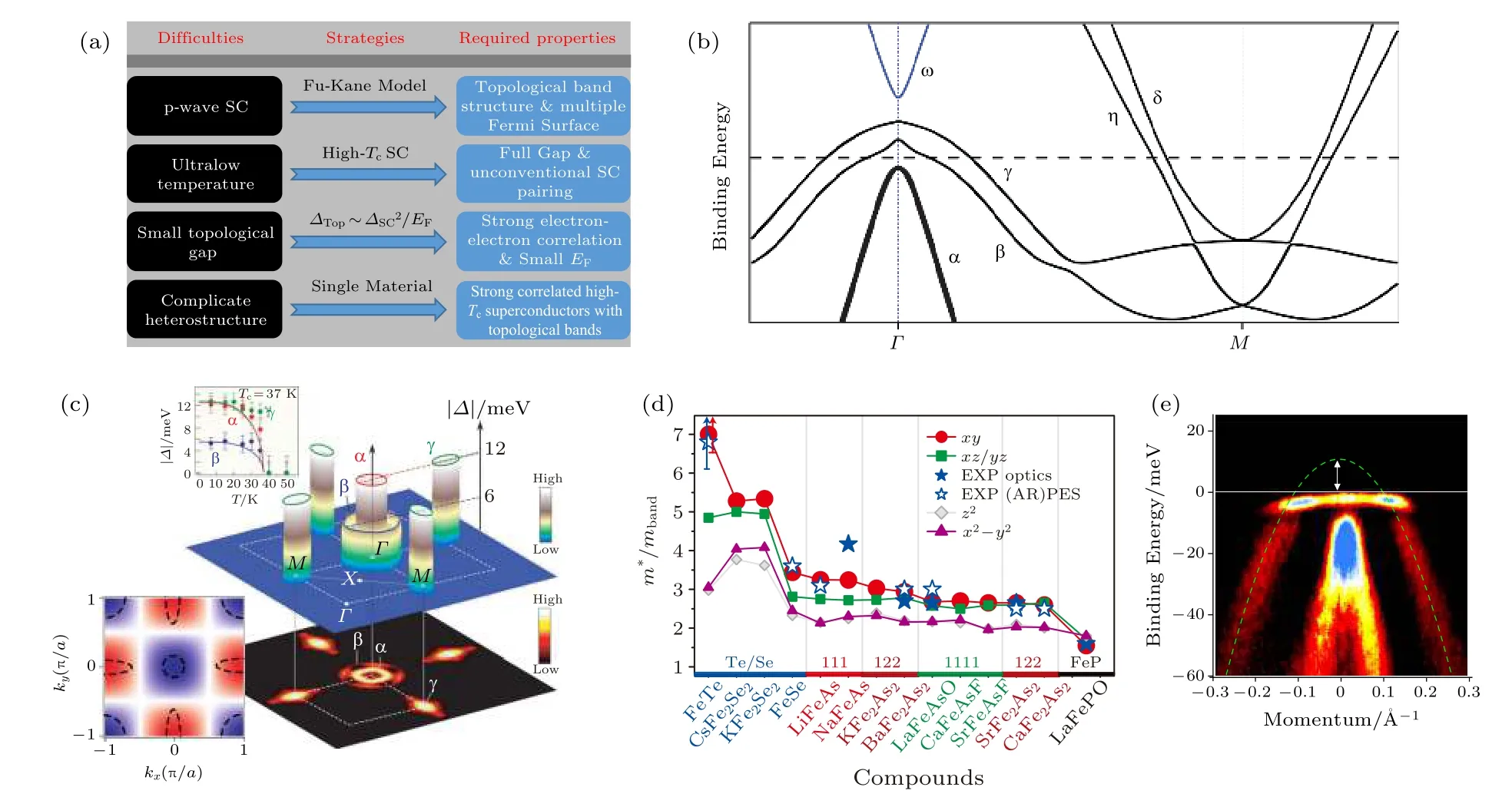
图 1 铁基超导体是更优的MZM载体材料 (a)在铁基超导体中寻找MZM的原始思路; (b)铁基超导的能带结构， 其中各能带的轨道成分分别为: α (dxz); β (dyz); γ (dxy); η (dxy); δ (dxz); ω (pz); (c)铁基超导的费米面以及超导配对对称性[74，76]; (d)铁基超导体的电子-电子关联[81]; (e)ARPES测量的Fe(Te， Se)单晶G点的能带结构[82]Fig. 1. Fe-based superconductors (FeSCs) as a better Majorana platform: (a) The original idea for searching Majorana zero mode(MZM) in FeSCs; (b) the typical band structure of FeSCs， the orbital characters of each band are as follows: α (dxz); β (dyz); γ (dxy);η (dxy); δ (dxz); ω (pz); (c) the typical Fermi surface and superconducting order parameters of FeSCs[74，76]; (d) the mass renormalization among different compounds， indicating strong electron-electron interactions in FeSCs[81]; (e) band structure near the G point of Fe(Te， Se) single crystals measured by ARPES[82].

本文旨在系统总结并详细介绍Fe(Te， Se)体系中演生涡旋MZM的思想起源和研究进展， 尝试搭建经典Majorana理论与新兴铁基超导载体之间的桥梁. 本文的结构安排如下， 第2节介绍拓扑能带理论以及表面态的实验观测[87，100，101]. 第3节讨论实验观测到的涡旋零偏压电导峰(ZBCP)究竟“是什么”. 将介绍检验实验， 从而确认ZBCP为涡旋MZM[102]. 第4节讨论涡旋MZM“为什么”在真实Fe(Te， Se)材料中演生. 将介绍涡旋MZM的波函数和准粒子中毒行为的仔细研究， 鉴别真实材料中的各种因素在演生涡旋MZM的作用[102]. 第5节讨论涡旋MZM的Majorana本质[105]. 将结合共振量子电导理论介绍涡旋MZM的粒子-空穴等价性的实验测量. 第6节讨论涡旋MZM的拓扑本质[104]. 结合全局涡旋束缚态的能量本征值及波函数分布特征， 详细介绍伴随涡旋MZM出现的涡旋束缚态半整数能级嬗移. 第7节转而关注“工程细节”. 实际测量发现Fe(Te， Se)的部分涡旋中没有MZM， 我们将综合分析可能的微观机制[104]， 这对铁基材料的未来应用具有一定指导意义. 第8节是总结和展望. 将简要综述新兴铁基超导载体的研究进展， 指出铁基超导涡旋走向拓扑量子计算亟须解决的问题.

2 Fe(Te， Se)单晶的拓扑能带

铁基超导体能带具有丰富的拓扑相[83，84，87，101].由于阴离子的pz轨道具有奇宇称， 原则上可以通过调节pz轨道能量和垂直色散程度， 使它在G-Z方向上与具有偶宇称的dxzdyzdxy铁离子能带发生交叉， 获得拓扑非平庸的能带反转. 根据交叉能带的角动量相同或不同， 可以分别定义拓扑绝缘体态和拓扑Dirac半金属态. 原理上， 铁基超导体中出现拓扑能带的核心要素是强层间耦合和强自旋轨道耦合(SOC). 这一机制并不是铁基超导体的专利， 本文注意到在1T相的过渡金属二硫化物类材料(比如 PtTe2， PdTe2， NiTe2等)中存在相似的拓扑能带形成机制[107-109]. 能带反转机理的复现性增加了铁基超导体拓扑能带理论的可信度. 原则上， 在理想的调控能力下所有铁基超导体都可以同时具有拓扑绝缘体态和拓扑Dirac半金属态. 第一性原理计算和ARPES实验观测发现铁基超导体家族中的某些组分天然满足能带反转要求. 本文下面以Fe(Te， Se)单晶为例， 介绍拓扑能带的形成机理以及相关实验进展.

2.1 拓扑能带形成机理

FeSe单晶的第一性原理计算如图2(a)所示[87].在不含SOC的情况下， 沿G-Z方向费米能级附近有三条能带， 它们的不可约表示分别记为: G2-(pz/dxy反键轨道)，G4+(dxy轨道)，G5+(dxz/dyz轨道). 在FeSe单晶中， 奇宇称的 G2-能带始终位于偶宇称能带上方， 没有拓扑能带反转发生. 理论上可以通过改变晶格参数的方法调控 G2-能带， 如图2(c)所示， 在Fe(Te， Se)单晶中， Fe原子dxy轨道平躺在Fe平面上(青色平面)， 电子云在c方向上延伸很小; 而Se原子pz轨道一头与Fe平面上的dxy轨道耦合， 另一头跨过范德瓦尔斯(vdW)间隙与相邻Se-Fe-Se层的pz轨道耦合. 通过改变阴离子与Fe平面的距离可以有效调控层内pd耦合和层间pp耦合的相对强度， 这两者的竞争将决定 G2-能带的行为. 对FeSe进行Te掺杂可以增加阴离子与Fe平面的距离， 这使得层内pd耦合变弱，pz/dxy反键轨道 G2-随即降低能量以适应这一变化.同时， Te掺杂使得层间pp耦合增强， 这导致 G2-能带获得更强的垂直色散. 在这两方面因素的共同作用下， 奇宇称的 G2-能带沿着G-Z方向穿越偶宇称的 G4+和 G5+能带， 在Z点发生拓扑能带反转(图2(d)). 在SOC作用下，G2-能带演化为 G6-， 主要由pz轨道组成; G4+能带演化为 G7+， 主要由dxy轨 道 组 成; G5+能 带 演 化 为 G6+和 G7+， 分 别 由dxz和dyz两条轨道组成.

DFT计算结果显示[87]， FeTe0.5Se0.5单晶中dxy能带( G7+)始终位于dyz能带( G7+)上方， 它们在G点都穿越费米能级， 因此奇宇称的pz能带沿着G-Z方向与偶宇称的铁离子能带有三个交点. 但是超高分辨率ARPES实验表明， FeTe0.55Se0.45单晶的G点只有一条体能带(dyz)穿越费米能级(图2(e))[101]， 这显然会影响G-Z能带反转的具体细节. 考虑到铁基超导体的能带具有轨道依赖的质量重整化特征[81]， dxy能带具有更大的重整化因子，这使得dxy能带展宽变小， 从而不跨越费米能级.dxy能带在G点附近与dyz能带相交， 由于它们属于相同的不可约表示， dxy与dyz能带的交叉点打开杂化能隙， 这一现象也被ARPES清晰地观测到(图2(e))[101]. 为了与实验保持一致， 理论学家利用k·p模型计算了FeTe0.55Se0.45单晶含SOC的准确能带结构(图2(f))[101]， 奇宇称的pz能带沿着G-Z方向与偶宇称能带有两个交点. 首先， pz能带和dxz能带具有相同的角动量， 同属相同不可约表示， 它们之间可以杂化从而在能带交叉点打开SOC能隙， 因此在费米能级附近可以定义非平庸的Z2拓扑不变量(强拓扑绝缘体态). Te原子掺杂增强了材料的SOC， 有利于稳定强拓扑绝缘体相.而pz能带和dyz能带角动量不同， 能带交叉点受晶体主轴旋转对称性保护， SOC不能使之打开能隙.受对称性保护的变宇称能带反转是非平庸拓扑Dirac半金属的典型特征， 因此在费米能级以上可以 定义拓扑Dirac半金属态.

2.2 拓扑绝缘体态的实验发现

使用超高分辨ARPES对FeTe0.55Se0.45单晶进行能带色散测量、光偏振极化测量、自旋分辨测量以及极低温测量， 实验证实了位于费米能级附近的拓扑绝缘体态[100]. 实验清晰地观测到了线性色散的Dirac表面态; 利用ARPES的矩阵元分析[76，110]，鉴定出了Dirac表面态的轨道信息; 通过自旋分辨实验直接观测到了Dirac表面态的自旋轨道锁定性质[25-27]; 最振奋人心的是， 在Dirac表面态费米波矢(kF)处测量的变温能量分布曲线表明Dirac表面态在超导转变温度(Tc≈ 14.5 K)以下打开各向同性超导能隙. 这表明FeTe0.55Se0.45单晶天然满足Fu-Kane模型的要求[24]， 从而可以规避构造异质结带来的困难(图1(a)). 实验还发现Dirac表面态具有非常小的EF， 暗示FeTe0.55Se0.45单晶演生的涡旋MZM具有很大的拓扑能隙.

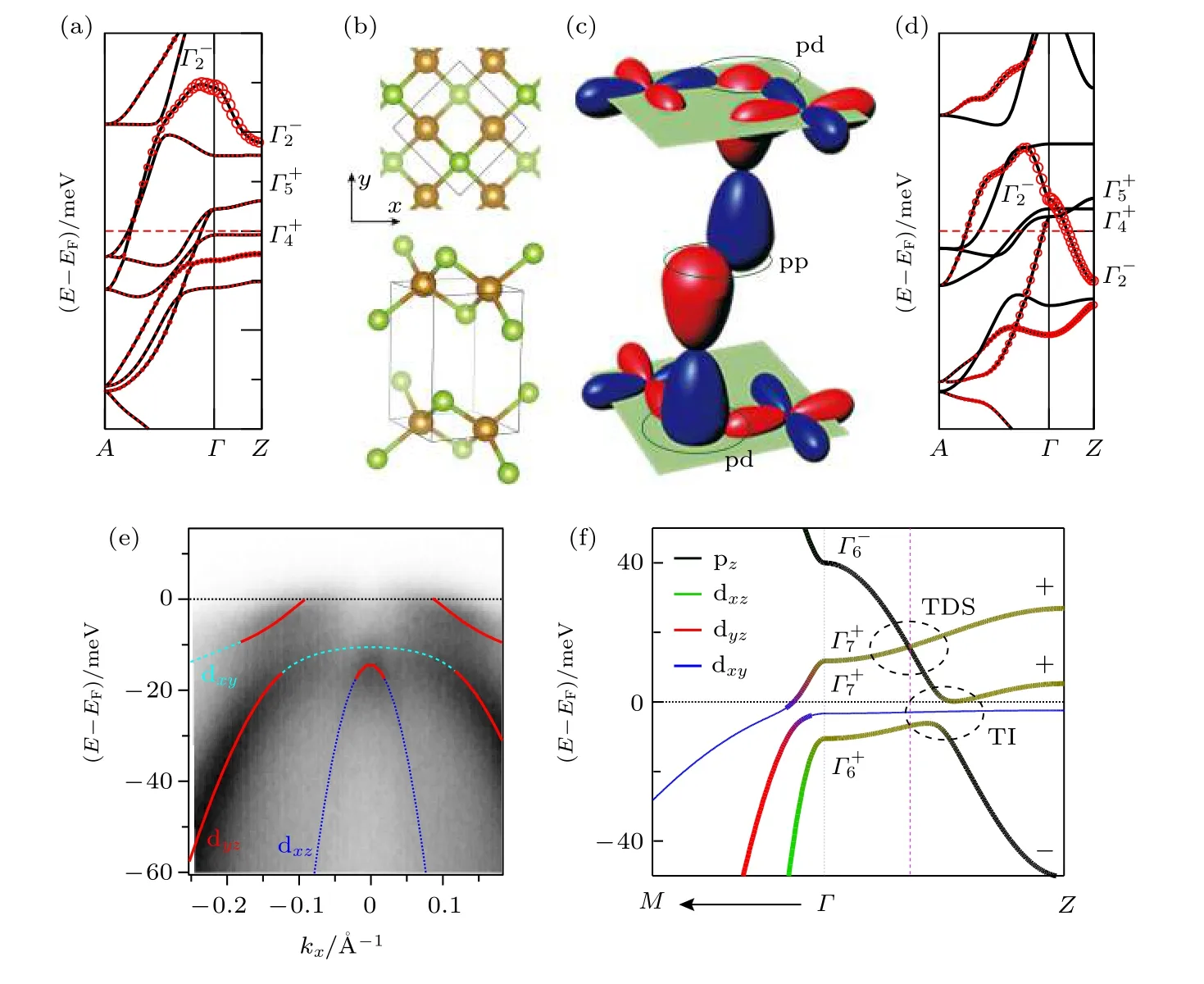
图 2 Fe(Te， Se)的拓扑能带结构与能带反转机制 (a) FeSe单晶的第一性原理计算(不含SOC)， 其中红圈的尺寸表示pz轨道的成分[87]; (b) Fe(Te， Se)的晶体结构[87]; (c)拓扑能带的形成机制[87]; (d) FeTe0.5Se0.5单晶的第一性原理计算(不含SOC)[87]; (e)超高分辨率激光ARPES测得的FeTe0.55Se0.45布里渊区中心的体态能带结构[101]; (f) Fe(Te， Se)能带的拓扑相(含SOC)， 其中TDS代表拓扑Dirac半金属， TI代表拓扑绝缘体[101]Fig. 2. The mechanism of topological band structure and band inversion of Fe(Te， Se): (a) First-principle calculation of band structure of FeSe (without SOC)， the size of red circles represents the components of pz orbital[87]; (b) crystal structure of Fe(Te， Se)[87];(c) band inversion mechanism and orbital overlapping in Fe(Te， Se)[87]; (d) first-principle calculation of band structure of FeTe0.5Se0.5 (without SOC)[87]; (e) experimental band structure around G in FeTe0.55Se0.45 measured by ultra-high resolution laser ARPES[101]; (f) realistic topological band structure in FeTe0.55Se0.45 (with SOC). TDS stands for topological Dirac semimetal， TI stands for topological insulator[101].

ARPES能够同时分辨电子的动量和能量信息， 直接获得能带结构， 因此被广泛应用在拓扑材料的表征中[111]. 众所周知[112，113]， ARPES的谱强度为

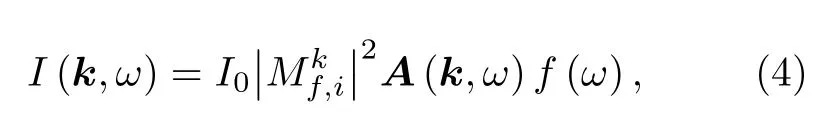
其 中 f (ω) 是费米-狄拉克函数，

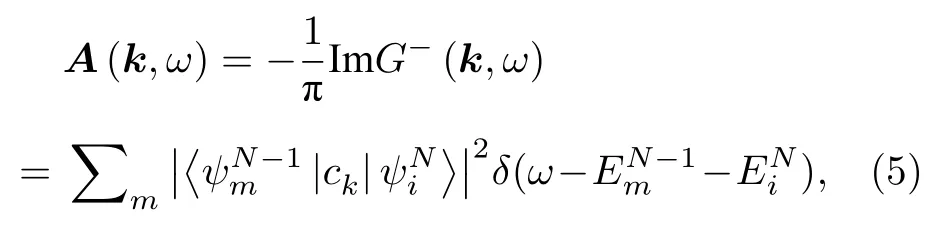
是材料的谱函数， 表示材料中电子被光子激发的概率;

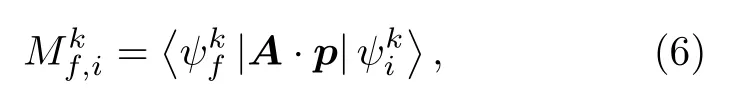
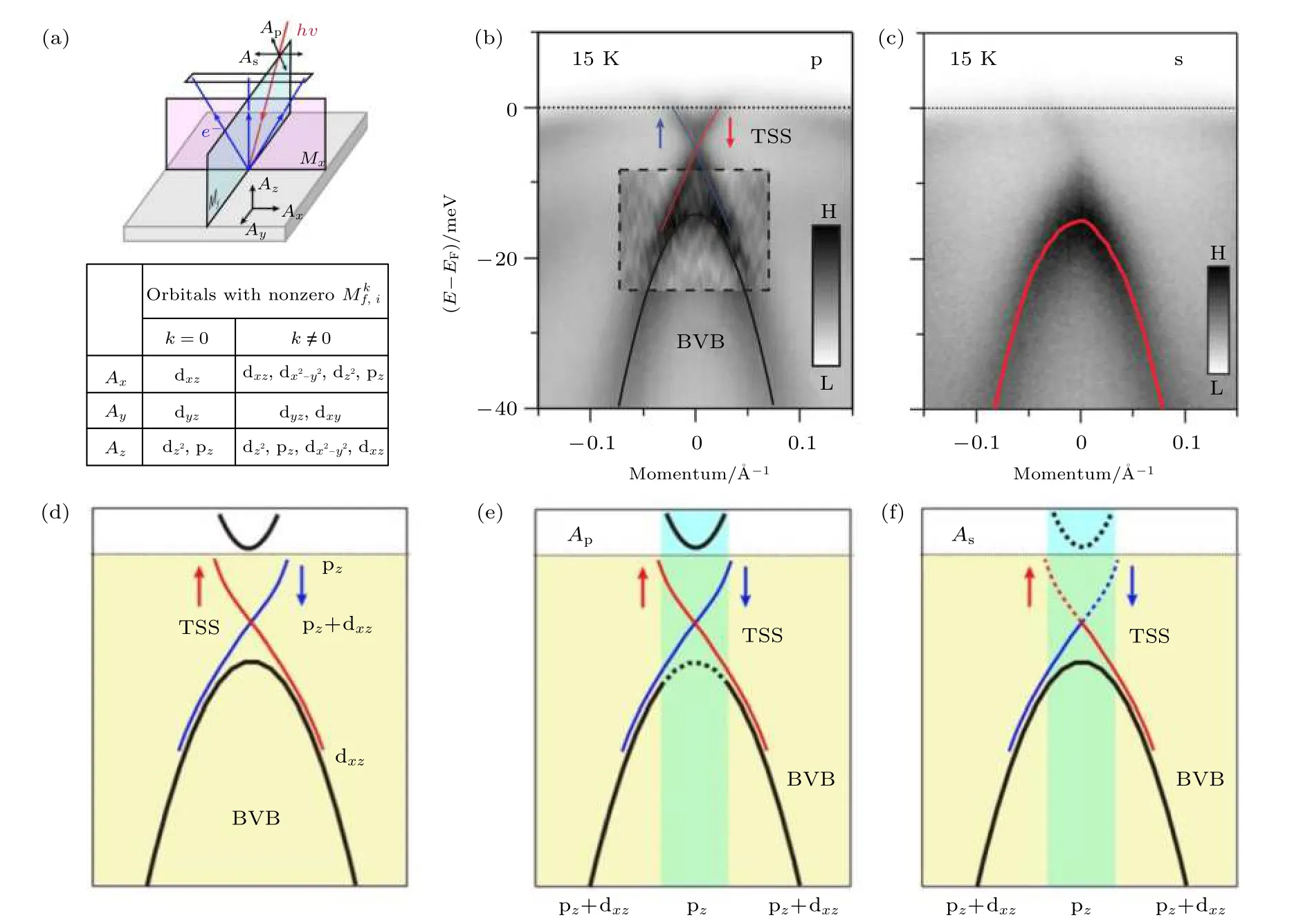
图 3 FeTe0.55Se0.45单晶中线性色散的Dirac表面态的实验观测[100] (a) ARPES光子偏振与轨道的选择性; (b) p偏振下观测到的Dirac表面态; (c) s偏振观测到的体态dxz能带; (d)G点能带的轨道特性分析; (e)， (f)两种偏振下轨道选择性分析， 其中底部的轨道标记代表当前条件下具有ARPES选择活性的轨道， 能带示意图中的虚线部分表示被矩阵元效应禁闭掉的能带Fig. 3. Experimental observation of the linear dispersion of Dirac surface states in FeTe0.55Se0.45[100]: (a) The matrix element effect which defines the selection rule of ARPES intensity， depending on relationship between photon polarization and electron orbitals;(b) the Dirac surface states observed under p-polarization; (c) the dxz bulk bands observed under s-polarization; (d) orbital characters around G in FeTe0.55Se0.45; (e)， (f) orbital character determined by the matrix element analysis under p- and s-polarization， respectively. The orbital characters marked at the bottom represent the active orbitals under certain polarization and momentum.The dashed parts in the band structure represent the intensity suppressed by the selection rule.

是光电效应矩阵元， 决定了ARPES实验的轨道选择性定则. 只有当 Mfk，i不为零时， 才有可观测的ARPES信号. 由于ARPES的出射光电子一般为平面波， 其波函数 ψfk相对于ARPES信号采集平面(即ARPES能量分析器的slit平面， 如图3(a)中的粉色平面所示)总是偶函数， 为了使ARPES信号强度不为零， 光子偏振 A ·p 和材料中电子轨道波函数 ψik相对于ARPES信号采集平面的对称性必须同奇同偶. 当光电子垂直发射时， 即测量G点时，ψfk相对于信号采集平面的垂直平面(如图3(a)中的蓝色平面)也为偶函数， 这时 A ·p 和 ψik相对于垂直平面的对称性也会影响选择定则. 图3(a)的表格总结了不同实验条件下的轨道选择性定则[100].Fe(Te， Se)单晶中的拓扑绝缘体态主要由pz能带和dxz能带的拓扑能带反转产生， 在自旋轨道耦合的作用下， 拓扑表面态的轨道特性主要由这两种轨道组成. 在G点附近， 预期的能带轨道组成如图3(d)所示. 在p偏振实验几何下， 光子极化方向同时包含Ay和Az， 这有利于pz轨道成分的观测， 但会压制G点dxz轨道的信号(图3(e)). p偏振下的实验结果如图3(b)所示， 可以清晰地观测到线性色散的Dirac锥能带结构， 而dxz能带顶比较模糊， 只能通过二次微分的方法加以分辨， 这一实验观测与矩阵元理论分析的预期结果一致. 而s偏振实验几何只含有Ax极化光子， 这使得G点附近的pz轨道的信号被强烈压制， 拓扑表面态几乎不可见， 与此同时， 由于s偏振对dxz轨道具有很好的选择性，在这一实验条件下可以很好地观测体态的空穴型dxz能带. s偏振下的实验观测与理论预期一致(图3(c)， 图2(e)). 超高分辨ARPES实验清晰地观测到了拓扑表面态的Dirac锥结构， 通过光子偏振测量发现SOC能隙下方的体态空穴型能带主要由dxz轨道构成， Dirac表面态的上半支主要由pz轨道构成， 而下半支混有pz和dxz两种轨道成分， 进而可以推测SOC能隙上方的体态电子型能带主要由pz轨道构成(图3(d)).

Dirac表面态( HTSIurface=σxky-σykx-μ) 具有本征的自旋轨道锁定性质， Dirac电子绕费米面一圈产生大小为π的自旋Berry相位(图4(a)). 这一行为也被当作鉴别拓扑绝缘体态的决定性证据之一. 如图4(a)所示， 实验选取Dirac表面态的一对费米点分别测量自旋极化能量分布曲线Cut 1和Cut 2 (图4(b)， 图4(c))， 在费米能级附近它们的自旋信号均发生了反转， 这表明相同动量位置上， 上下半支Dirac表面态自旋极化不同， 另外在相同的能量上Cut 1与Cut 2的自旋也相反， 这些结果表明超高分辨ARPES观测到的线性能带具有自旋轨道锁定性质， 这是Dirac表面态的重要特征.

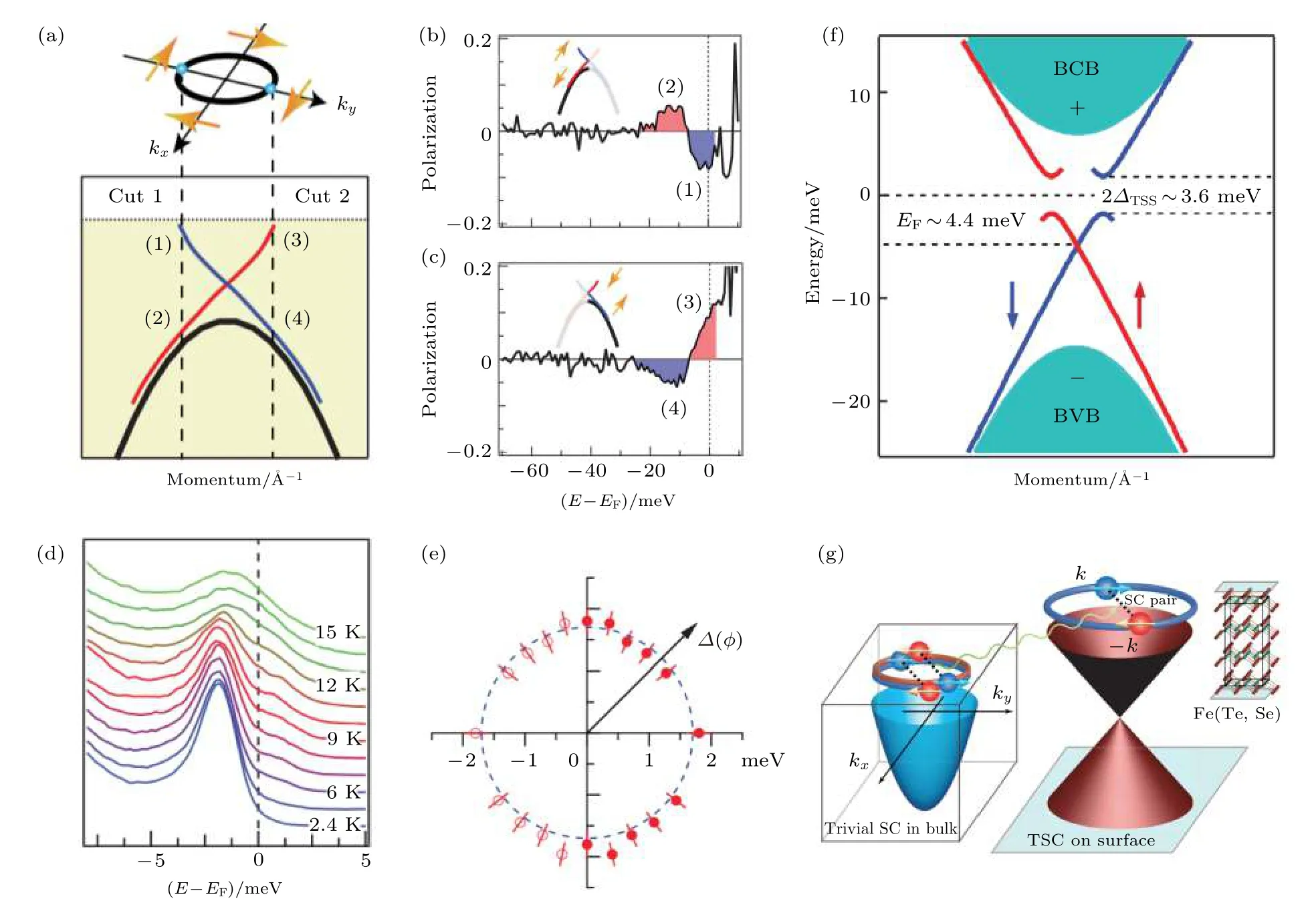
图 4 自旋轨道锁定的Dirac表面态发生各向同性超导配对 (a) FeTe0.55Se0.45中Dirac表面态的自旋轨道锁定性质[100]; (b)自旋分辨的ARPES实验结果: 测量的动量位置为(a)图标注的Cut 1[100]; (c)自旋分辨的ARPES实验结果， 测量的动量位置为(a)图标注的Cut 2[100]; (d) Dirac表面态kF处的能谱变温实验， 数据表明Dirac表面态在低温下打开超导能隙， 且该能隙关闭的温度大致与体态超导临界温度相同[100]; (e) Dirac表面态的超导能隙是各向同性的[100]; (f)总结FeTe0.5Se0.5单晶的拓扑绝缘体态能带的主要观测， 其中有拓扑能带反转、线性Dirac色散、自旋轨道锁定、大超导能隙、小费米能[102]; (g) FeTe0.55Se0.45单晶中的 Dirac表面态感受到来自体态的s ±波超导近邻效应， 满足Fu-Kane模型的要求[100]Fig. 4. Spin-momentum locking and isotropic superconducting gap on the Dirac surface state: (a) The spin-momentum locking feature in FeTe0.55Se0.45 single crystal[100]; (b)， (c) spin-resolved ARPES data measured along Cut 1 and Cut 2 in panel (a)，respectively[100]; (d) temperature dependent energy distribution curves measured at kF of the Dirac surface state indicating a superconducting gap of the Dirac surface state opens below 14.5 K， which is the bulk Tc[100]; (e) isotropic superconducting gap on the Dirac surface state[100]; (f) summary of the main observations of the Dirac surface state on FeTe0.55Se0.45 single crystal， i.e. topological band inversion， linear dispersion， spin-momentum locking， large superconducting gap， small Fermi energy[102]; (g) the Dirac surface state of FeTe0.55Se0.45 single crystal acquires an effective spinless pairing due to the proximity effective from s ±-wave bulk superconductivity， which satisfies all of the requirements of Fu-Kane model[100].

为了研究Dirac表面态与体态超导电性的耦合， 实验进一步测量了Dirac表面态kF处的超导能隙. 早期实验表明， FeTe0.55Se0.45单晶的超导配对机制为s ± 波[77，114]， 其超导序参量在动量空间的分布如图1(c)所示. 由于Dirac表面态主要集中在布里渊区中心(kF≈ 0.02 Å—1)， 表面Dirac电子感受到的体态超导电性可以近似看作常规s波超导. 理论预期FeTe0.55Se0.45单晶的体态超导通过k空间的超导近邻效应赋予Dirac表面态s波超导配对. 早期极低温ARPES实验观测发现Fe(Te，Se)单晶的G点附近存在两个超导能隙(Δ1=1.7 meV， Δ2= 2.5 meV)， 在M点附近存在一个超导能隙(Δ3= 4.2 meV)[115]. 实验分析发现， 考虑第三近邻反铁磁交换关联(J3)的强耦合自旋交换模型[66]给出的能隙方程，Δ=|J2cos(kx)cos(ky)-J3[cos(2kx)+cos(2ky)]/2| ， 可以很好地描述并拟合实验观测到的Δ2和Δ3， 拟合得到的 J2/ J3值与中子散射测量的结果接近[116]. 然而Δ1同时具有最小能隙值和最小的kF， 这大大偏离了J1-J2-J3模型的预期[115]. 这些早期结果暗示Δ2和Δ3遵循s ± 超导配对， 而Δ1可能具有不同的来源. 得益于ARPES动量能量分辨率的提升， FeTe0.55Se0.45单晶的超导能隙如今获得了更加清晰的实验观测[100]. 如图4(d)所示， 新的实验数据显示Dirac表面态在低温下打开1.8 meV的超导能隙(ΔSurface= 1.8 meV). 变温实验显示， 表面态超导能隙的关闭温度约为14.5 K. 进一步实验发现， Dirac表面态的超导能隙呈现各向同性分布(图4(e)). 具有最小kF的Dirac表面态上打开的超导能隙小于所有的体态超导能隙， 这一现象显然与s ± 超导配对相左， 但符合k-近邻效应导致Dirac电子配对的图像. 新观测到的ΔDirac与早期实验得到的Δ1行为高度符合，这也合理解释了Δ1不能被J1-J2-J3模型标度的问题. 综合其他文献的结果[77，82，99-102，115-119]， 本文总结了FeTe0.55Se0.45单晶超导能隙的情况如下:G点 附 近，ΔSurface=1.8meV，ΔdByuzlk=2.5meV ;M点附近，ΔMBulk=4meV . 另外值得一提的是， 表面态的超导能隙更容易被表面敏感的实验手段(如ARPES， STM)观测到[119].

图4(f)总结了ARPES观测到的FeTe0.55Se0.45单晶中拓扑绝缘体态的主要参数， 除去基本特征外， 有两个细节值得注意: 其一， 拓扑绝缘体态的SOC能隙约为20 meV， 远远小于经典强拓扑绝缘体的SOC能隙(在Bi2Se3中约为300 meV)[25]; 其二， 拓扑表面态的Dirac点恰好出现在费米能级附近， 免除了精细调节化学势(chemical potentail)的麻烦. FeTe0.55Se0.45单晶Dirac表面态的费米能仅为约4.4 meV， 这使得Fe(Te， Se)的拓扑表面态具有很大的Δ/EF比值(约0.5)， 与之相比， 在Bi2Se3中这一比值极小， 约为10-3—10-2. Fe(Te，Se)中Dirac表面态的这一特征为实现大拓扑能隙MZM带来了初次曙光.

Fe(Te， Se)单晶表面自旋轨道锁定的Dirac电子受到体态自旋简并电子的s ± 超导电性的超导近邻效应产生s波超导配对， 这等价于二维的无自旋手性p波拓扑超导体(图4(g)). Fe(Te， Se)单一材料自然实现了Fu-Kane模型的所有要求，在常规超导涡旋里将会有理论预期的单个MZM(图6(a)). 正如Lee[120]评价， Fe(Te， Se)单晶是大自 然的礼物!

2.3 Dirac半金属态的实验证据

如图2(f)所示， Fe(Te， Se)中的Dirac半金属态由pz轨道和dyz轨道构成， Dirac点位于费米能级以上， 无法利用ARPES直接测量体态Dirac锥能带结构. 然而对于主轴旋转对称性保护的Dirac半金属[121]， 表面费米弧和体态Dirac能带在(001)表面重叠在一起， 自旋简并的体态Dirac能带上也可以观测到自旋极化信号(图5(c))[122-124]，因此ARPES实验可以通过反常的体能带自旋极化信号证明Dirac半金属态的存在. 前面提到， 由于dxy能带具有很大有效质量， 它与dyz能带在G点附近交叉并打开杂化能隙(图5(a))， dyz能带的上半支向上延伸参与形成Dirac半金属态. 如图5(b)所示， 自旋分辨ARPES实验在dyz能带的上半支观测到了自旋极化信号， 且在G点两侧自旋极化方向相反. 通过分别测量kx和ky方向dyz能带的自旋极化， 实验发现该费米面上的自旋织构呈螺旋分布(图5(d)， 图5(e)). 这一行为是由于Dirac半金属体能带和表面费米弧投影到(001)面相互重叠导致的. 另外， 实验发现dyz能带的下半支不存在自旋极化现象(图5(a)和图5(b))，如图5(d)和图5(e)所示， 在—20 meV以下不存在自旋极化信号， 这在一定程度上可以排除dyz能带上半支中观察到的自旋极化现象来源于其他效应的可能. 这些证据支持Fe(Te， Se)本征费米能级以上存在Dirac半金属态.

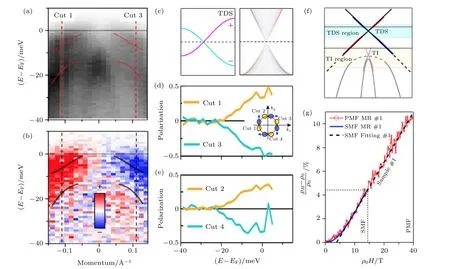
图 5 FeTe0.55Se0.45单晶中Dirac半金属态的实验观测[101] (a)， (b)G点附近能带自旋积分和自旋分辨信号; (c)主轴对称性保护的Dirac半金属(001)面的能带结构， 自旋极化的表面态与体态混合; (d)， (e)体态Dirac能带(dyz)四个代表性kF上的自旋极化ARPES信号， 实验发现体态Dirac能带具有螺旋自旋特征; (f) FeTe0.55Se0.45单晶中的拓扑非平庸能带结构， 费米能级附近为拓扑绝缘体态， 费米能级以上有Dirac半金属态; (g)Dirac半金属态的输运证据. 在高磁场下， 磁阻随磁场呈线性变化， 表明材料达到量子极限， 这是拓扑能带的证据. 磁阻测量在16 K下进行. 图中PMF和SMF分别代表在脉冲磁场和恒稳磁场实验条件下测量的结果Fig. 5. Evidence of Dirac semimetal phase in FeTe0.55Se0.45 single crystal[101]: (a)， (b) The spin-integrated and spin-resolved ARPES spectrum around G respectively; (c) the projected band structure on the (001) surface of a C4 symmetry protected Dirac semimetal.The spin polarized surface states are mixing with the bulk bands; (d)， (e) spin polarization of the dyz bulk band measured on four representative kF around the Fermi surface (as indicates in the insert). It is clear that the dyz bulk band has the helical spin texture;(f) summary of the topological band structure along the in-plane momentum. There are a strong topological insulator phase around the Fermi level and a topological Dirac semimetal phase above it; (g) the transport evidence of Dirac semimetal phase in FeTe0.55Se0.45 single crystal. The linear transverse magnetoresistance indicates the incorporation of bulk Dirac electrons. The transport experiments were carried at 16 K. The PMF and SMF represent pulse and static magnetic field respectively.

由于dxy能带沉到费米能级以下， 费米能级附近的输运行为主要由Dirac能带决定， 这有利于观测Dirac体能带带来的奇异磁阻输运行为. 如图5(g)所示， 实验发现FeTe0.55Se0.45单晶的霍尔磁阻出现反常. 在6 T以下， 磁阻随磁场呈半经典的二次型关系变化， 而在6—40 T的区间里出现了奇异的线性磁阻行为. 奇异的线性磁阻行为有多种解释，比如在存在平均效应的多晶材料[125]、强无序系统[126]中都观测到了线性磁阻， 然而这些情况显然不适用FeTe0.55Se0.45单晶. 朗道能级量子极限下的磁阻输运也呈线性[125，127]. 朗道能级的简并度随着磁场强度增加而上升(单位面积内的简并数密度g=eB/h)， 当所有电子只占据最低朗道能级时，称为朗道能级的量子极限. 实现量子极限不仅需要很强的磁场(以至于最低朗道能级可以容纳所有电子)， 而且最低朗道能级与第一激发态之间的能量间距ΔELL需要大于EF和温度涨落kBT[128]. 对于常规的二次型能带， 朗道能级满足谐振子分布， 即， 其中 m*为有效质量， μ为二次型能带的化学势. 为了实现量子极限， 需要， 利用Fe(Te， Se)的实验参数本文估计出常规抛物线能带的量子极限临界磁场约为 60 T (估算参数为 T = 16 K，m*=5me)[81，100，101].显然， 常规抛物线能带不足以在有限的实验条件下实现量子极限. 然而对于具有线性色散的Dirac能带， 朗道能级满足其中 ED为Dirac点的能量，νF为Dirac表面态的费米速度.， 本文通过简单估算得出Dirac能带情况下量子极限临界磁场约为2.8 T (估算参数为T = 16 K， kF= 0.1 Å—1)， 这与实验事实相匹配. 值得一提的是， 在早前的FeTe0.6Se0.4单晶磁阻测量中[128]， 线性磁阻行为在磁场高于2 T后出现， 这与我们的估计值更为接近. 因此图5(g)所示的磁阻行为可以用Dirac半金属态很好地解释.

Fe(Te， Se)单晶的拓扑能带随后被其他实验组验证[129，130]. 最后， 本文将Fe(Te， Se)单晶能带的拓扑相总结在图5(f)中. Fe(Te， Se)单晶丰富的拓扑能带为MZM的出现提供了新的舞台. 由于铁基超导正常态电子迁移率较高， 其化学势一般很难通过电场栅压等常规方式进行调控[131]， 通常情况下实验上只能研究Fe(Te， Se)单晶处于本征费米能级附近时的性质. 本文下面将主要介绍拓扑绝缘体态(位于费米能级附近)演生的涡旋MZM.

3 Fe(Te， Se)单晶中涡旋MZM的实现

结合前面的介绍可知， MZM会以束缚态的形式出现在FeTe0.55Se0.45单晶的超导磁通涡旋中[24，100]， 在态密度谱上表现为超导能隙内的零能峰(图6(a)). 由于FeTe0.55Se0.45单晶的体态能带和Dirac表面态都具有很大的Δ2/EF， 因此我们预期在磁通涡旋中MZM与最低能CdGM束缚态之间会有很大的拓扑能隙， 这有利于实验实现纯的单个MZM.

STM具有亚Å的空间分辨率[132，133]， 在真空单粒子隧穿条件下， 针尖与样品之间的隧穿电流为

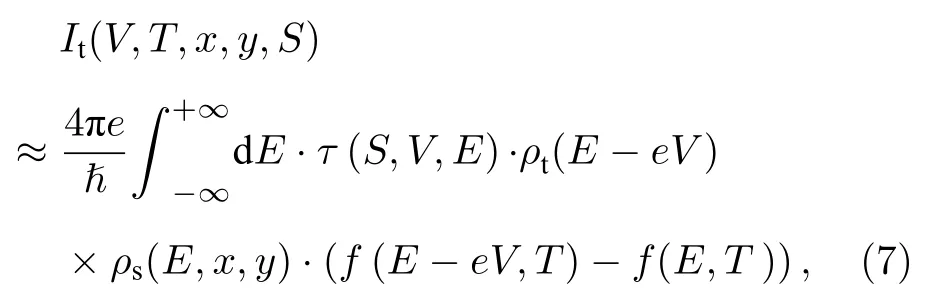
其中V是隧道结偏压; T是温度; x， y是样品的面内位置; S是针尖与样品的间距; τ 是隧穿矩阵元，当针尖波函数为各向同性的s波时， 隧穿矩阵元可以写成

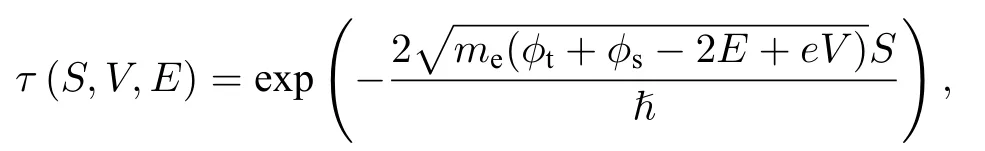
φt和 φs分别是针尖和样品的功函数; ρt是针尖态密度; ρs是空间分辨的样品局域态密度; f(E， T)是费米-狄拉克函数. τ 在小偏压范围内可以近似认为与偏压V无关， 当针尖位置固定且针尖态密度为常数的条件下， 样品的局域态密度可以通过STM的微分电导谱进行直接测量， 这时容易证明，. 因此STM非常适合用来检验磁通涡旋中是否存在MZM， MZM会以ZBCP的形式出现在dI/dV谱上.

实验上使用极低温强磁场STM系统测量了超高真空原位解理的FeTe0.55Se0.45单晶[102]， 如图6(b)所示， 在FeTe0.55Se0.45表面上可以观测到非常好的原子晶格像. 由于Se-Fe-Se“三明治”基块之间的间隙由vdW力连接， 相互作用很弱，FeTe0.55Se0.45单晶将从vdW间隙解理， STM观测到的表面为Se/Te原子面. 具有大原子半径的Te原子高度较大， 在STM图上表现为亮点， 而原子半径相对较小的Se原子高度小， 在STM图上表现为暗点. 这表明实验具有很好的空间分辨能力， 有利于测量涡旋MZM束缚态并分辨其波函数特征. 如图6(c)所示， 在0.5 T垂直磁场作用下，在STM零偏压电导绘图数据上可以观测到磁通涡旋晶格， 这是第二类超导体的重要特征[10].STM微分电导谱直接测量的是局域态密度， 因此STM观测到的磁通涡旋尺寸被超导相干长度(ζ)定义. 这与扫描磁力显微镜、扫描霍尔显微镜等磁学测量手段不同， 它们测量到的涡旋尺寸被超导磁穿透深度()所定义. 在图6(c)红框所标记的磁通涡旋中心测量的dI/dV谱上出现了非常尖锐的ZBCP， 且该ZBCP孤立在超导能隙中间， 看起来很像是单个零能束缚态; 而在远离涡旋中心的位置， dI/dV谱又恢复到正常的超导能隙谱形. 在超导体拓扑缺陷上观测到零能束缚态是MZM存在的重要标志[24]， STM实验的空间分辨能力使得该零能峰相较于在纳米线等体系中依赖输运手段观测到的ZBCP具有更优的空间测量精度和更好的Majorana可信度[33，134].

3.1 涡旋零能束缚态的真实性检验

考虑到Fu-Kane模型的要求， 为了验证观测到的ZBCP为MZM， 实验上需要确定观测信号是真实的单个涡旋零能束缚态， 我们做了如下检验.

第一， 实验上确保观测到的能隙内束缚态是真正的涡旋束缚态， 而不是由于杂质、不均或无序等因素导致的超导准粒子束缚态. 在进行磁通涡旋测量之前， 实验上首先对材料进行零场表征， 通过测量形貌图、零场dI/dV谱和零场零偏压电导绘图，选择超导能隙谱学特征好、零偏压电导几乎为零的干净区域施加磁场进行进一步实验. 如图6(e)所示， 左侧为2 T下观测到的磁通涡旋， 在涡旋中心存在ZBCP(图6(d))， 右侧为在相同空间位置测量的零场零偏压电导绘图， 数据显示该区域零场零偏压态密度几乎为零， 不存在其他缺陷导致的超导准粒子束缚态， 因此在图6(d)中观测到的态密度全部由磁通涡旋导致. 为了进一步验证这一推论， 在含有ZBCP的涡旋中心位置进行了改变隧道结电阻的dI/dV谱测量(图6(f))， 其中隧道结电导由GN≡It/Vs定义， 由于STM针尖的自反馈调节， 越大的隧道结电导对应越小的针尖-样品间距和越大的隧穿耦合强度. 实验发现， 在隧道结电导改变三个数量级(以Majorana量子电导2e2/h为单位)的幅度下， 零能峰始终稳定. 这一行为符合涡旋束缚态的预期， 然而对于杂质、不均或无序等缺陷导致的超导准粒子束缚态， 束缚态能量在多数情况下会随着隧穿耦合强度改变而改变. 例如， 杂质产生的束缚态可以等效看作是超导/半导体混合纳米线末端量子点中的安德烈夫(Andreev)束缚态，改变隧穿耦合强度等价于改变量子点的化学势， 这会导致束缚态能量改变[135].

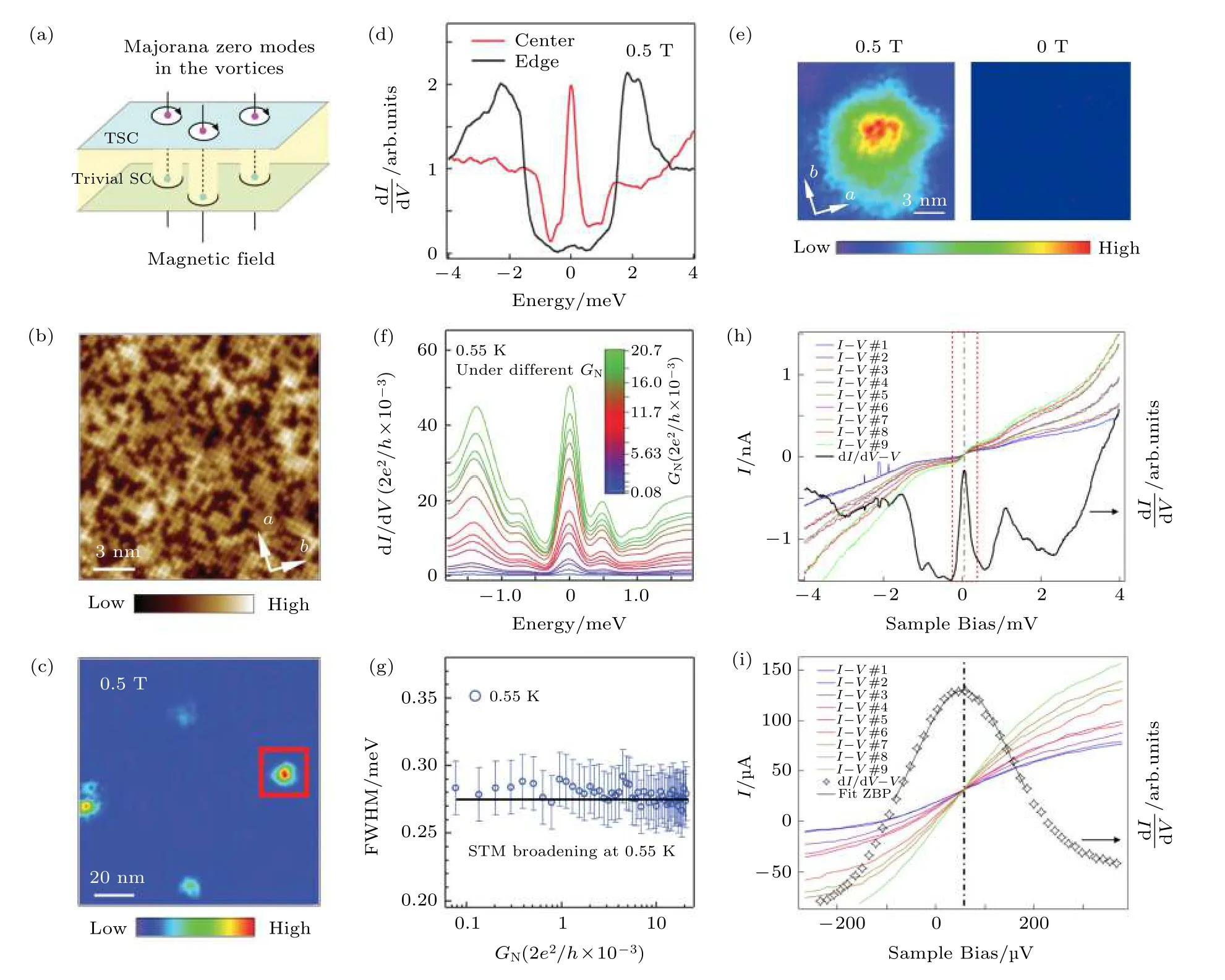
图 6 FeTe0.5Se0.5单晶超导磁通涡旋中MZM的发现 (a)理论预期MZM出现在 FeTe0.5Se0.5单晶的超导磁通涡旋中[100];(b) STM测量的FeTe0.5Se0.5单晶表面形貌图[102]; (c)零偏压电导绘图， 可以观察到涡旋晶格[102]; (d)部分涡旋中心存在尖锐的ZBCP[102]， 在(c)中红框选中的涡旋中心测量的dI/dV谱如红色曲线所示， 在该涡旋边缘测量的dI/dV谱如黑色曲线所示;(e)， (f)涡旋零能束缚态的真实性检验之一: 测量到的束缚态是纯净的涡旋束缚态; (e)加场测量前， 先在零磁场下利用dI/dV谱和零偏压电导绘图的方法检验所选区域， 选择无杂质的区域进行涡旋测量， 左图为2 T下零偏压电导绘图测到磁通涡旋， 右图为0 T下在与左图同样空间位置测量的零偏压电导绘图[102]; (f)ZBCP在不同隧道结电阻条件下稳定存在[102]; (g)涡旋零能束缚态的真实性检验之二: ZBCP的半峰全宽接近系统分辨率， 是真实的单峰[102]; (h)， (i)涡旋零能束缚态的真实性检验之三: 测量到的束缚态是真正的零能态， 其中(h)为STM直接测量到的I(V)曲线和lock-in输出的dI/dV(V)曲线未经校准过的原始数据[102]; (i)为(h)中红框区域的放大显示[102]Fig. 6. The discovery of vortex Majorana zero mode in FeTe0.55Se0.45 single crystal: (a) The theoretical prediction of vortex MZMs in FeTe0.55Se0.45 single crystal[100]; (b) STM topography of FeTe0.55Se0.45 single crystal[102]; (c) zero-bias conductance map which shows vortex lattice[102]; (d) a sharp zero-bias conductance peak measured at the center of a vortex. In order to make sure the observation is indeed a zero energy vortex bound state， three careful checks are listed as follows. First of all， to make sure that the signal measured is indeed from vortex bound state[102]: (e) ZBC map after and before applying a magnetic field. It shows the local environment of the vortex is clean and free of impurities[102]; (f) ZBCP is stable under different tunneling barriers. Secondly， to make sure that the observed ZBCP is truly a single peak[102]; (g) FWHM of ZBCP measured under different tunneling barriers; (h)， (i) the observed ZBCP is truly a zero mode[102]. (h) is the simultaneous measured I(V) curve and dI/dV curve on the center of a vortex core[102]， (i) is the enlarged display of red box area in Fig. (h).

第二， 实验上确保观测到的能隙内束缚态是真正的单个量子态， 而不是多个近零能峰的混合. 通过对图6(f)中的数据进行拟合， 实验上提取了零能峰的半峰全宽(FWHM)在不同隧道结条件下的行为. 实验发现测量到的FWHM小于0.29 meV， 且随着隧道结的改变基本不变(图6(g)). 通过校准系统分辨率， 实验确定相同条件下系统的总能量展宽约为0.28 meV[102]， 这不仅表明测量到的ZBCP的展宽主要由系统分辨率决定， 而且表明ZBCP的峰宽几乎达到了系统的综合分辨率极限， 强烈支持观测到的ZBCP是真正的单个量子态. 在图6(f)实验涵盖的隧道结范围内隧穿耦合强度依然很弱， 利用标度理论(详细介绍见第5节)对不同隧道结条件下的电导值进行拟合[102]， 可以估计由隧穿耦合强度( Gt)决定的Majorana本征展宽约为， 它的值远小于温度展宽(3.5kBT )和仪器分辨率. 因此图6(g)中显示的FWHM行为描述了弱耦合隧穿条件下单个量子态的峰宽变化. 另外值得一提的是， 在强耦合条件下FWHM将随隧穿耦合强度变大而增大， 其具体行为与隧穿耦合强度与温度以及耗散强度的匹配关系有关(详见5.1节).

第三， 实验上确保观测到的能隙内束缚态是真正的零能模. 众所周知， STM技术存在示读零点漂移的问题， 即仪器读到的电流电压零点并非物理真实值. 为了确保测量到的ZBCP是真正的零能模，需要对STM的零点漂移进行仔细校准. 在小偏压下电流和电压满足线性关系， 因此在不同隧道结条件下测量的I(V )曲线的交点就是真实的电流和电压零点. 利用这一方法， 在存在ZBCP的涡旋中心测量了不同隧道结条件下的I(V )曲线， 并将其与lock-in同步输出的dI/dV曲线进行对比(图6(h))，将图6(h)中红框部分的谱放大画在图6(i)中. 显然， dI/dV曲线的峰位与I(V )曲线的交点精确符合 ， 误差仅为dI/dV曲线的采点间隔(14 μeV).

3.2 甄辨零偏压电导峰的平庸解释

通过上述仔细检验可以确定， STM实验在具有超导拓扑表面态的材料上观察到了单个孤立的零能涡旋束缚态， 这就是Fu-Kane模型中的涡旋MZM. 然而， 零偏压电导峰时常存在于超导混合结构的凝聚态物理实验中， 这使得鉴定ZBCP为MZM变得十分困难. 虽然拓扑能带的观测和上述三个条件的确定已经强烈指向ZBCP为MZM， 为了严谨起见， 本文在这里罗列并讨论其他可能导致ZBCP的机理. 这些机理曾经在其他体系中对鉴定ZBCP为MZM造成困难.

1)相干Andreev反射导致ZBCP[136-138]. 其中最主要的机制是无反射Andreev隧穿， 这一机制的核心是在Andreev重反射过程中空穴和粒子准粒子的相位共轭. 在比较无序的超导界面上，Andreev反射产生的空穴可以沿着电子入射路径返回并与之相干， 从而导致电导增强. 这一效应会被磁场产生的额外相位破坏.

2)非相干Andreev反射的累积效应也可以产生ZBCP[139，140]. 处在弱耦合条件下的实验不利于非相干Andreev反射的发生.

3)近藤效应[141-144]. 传导电子在经过磁性杂质时发生自旋反转共振， 从而产生零能态密度. 近藤效应的发生需要有正常态的传导电子以及自旋双重态的磁性杂质， 且近藤共振ZBCP在磁场下劈裂[144].

4)约瑟夫森电流[145-148]. 超导库伯对隧穿过程在dI/dV曲线上表现为尖锐的ZBCP并伴有负电导出现， 这一现象可以被热涨落下的约瑟夫森模型很好地解释[147，148]. 使用非超导金属针尖的STM实验不能产生约瑟夫森电流.

5)无序导致的零能模[149-153]. 其中最主要的机制是Class-D弱反局域化. 当系统的尺寸L大于电子平均自由程l但小于电子相位相干长度lφ时，电子输运行为满足量子弥散输运. 在常规材料中，量子弥散输运导致弱局域化， 这也被看作是安德森局域化的前驱体[154]. 在拓扑材料中， 额外的π几何相位使得材料发生弱反局域化， 产生零偏压电导峰[155]. 通常情况下， 磁场会破坏弥散输运的电子相干， 从而抑制常规弱(反)局域化输运的发生. 但是在时间反演对称性破缺的Class-D超导体中，Andreev反射过程中的电子和空穴路径也可以满足量子弥散输运的相干条件， 从而产生弱反局域化零能电导峰[150，151]. 原则上， Fe(Te， Se)单晶中可能存在该机制， 但是得益于STM的空间分辨能力，实验上可以通过零场检验选择更加有序的区域进行测量， 规避这一机制的风险.

6)电荷势场起伏导致的零能Andreev束缚态[156-159]. 这一现象普遍存在于纳米线体系的末端量子点中[34，160]. 原则上Fe(Te， Se)单晶中可以存在这一机制， 但借助零场检验的方法选择更加有序的区域进行测量， 可以有效规避该机制带来的风险. 如果ZBCP是电荷势场起伏导致的， 那么在选定空间位置的零场测量下就应该出现.

7)单个磁性杂质的强耦合Yu-Shiba-Rusinov束缚态[161，162]. 实验上可以选择不存在磁性杂质的位置进行涡旋测量， 规避这一风险(3.1节).

8)非常规超导体的零能表面Andreev束缚态[163-174]. 当Andreev隧穿方向上存在水平超导能隙节线时， 粒子和空穴之间的π相位相干产生零能Andreev束缚态， 比如 〈110〉 隧穿测量下的d波高温超导体等. Fe(Te， Se)单晶垂直隧穿测量中不存在超导相位的变化.

9)当涡旋束缚态的能级间距很小时， 多个近零能束缚态挤在零偏压附近， 有限能量分辨率的条件下造成ZBCP的假象[13-15，175]. 这一现象常见于常规s波超导体(如NbSe2)的磁通涡旋中. 我们观测到的ZBCP的峰宽接近系统能量分辨极限， 不像是多个峰的卷积. 后面第6节会介绍Fe(Te，Se)单晶中观测到的分立涡旋束缚态能级， 可以安全排除这一可能.

综上所述， 利用极低温强磁场STM系统，STM实验在FeTe0.55Se0.45单晶中发现了涡旋MZM. STM技术具有优秀的能量和空间分辨率以及温度、磁场、隧穿条件等多维度的可调性， 这使得仔细研究涡旋MZM的性质和行为成为可能， 不仅有利于加深我们对MZM的理解， 也方便进一步证明FeTe0.55Se0.45单晶磁通涡旋中观测到的Z BCP是MZM.

4 演生涡旋MZM: Fe(Te， Se)单晶中的催生和破坏因素

由第1节的介绍可知， Fu-Kane模型是二维模型， 研究了只存在Dirac表面态的情况下， 二维平面上的零维磁通涡旋中MZM的演生[24]. Fu-Kane模型的简化处理敏锐地抓住了物理问题的核心， 避免引入次要因素干扰Majorana核心物理的阐述.然而在实际实验中使用的单晶样品(例如Fe(Te，Se))是三维材料(自赋性拓扑超导体)， 在施加垂直磁场时， 不仅在材料的二维表面上存在零维磁通涡旋(即STM观察到的， 图6(c))， 在材料体内也存在贯穿材料的一维磁通涡线[12]. 严格说来， 表面观察到的零维磁通涡旋并不孤立，而是一维磁通涡线的末端. 再者， FeTe0.55Se0.45单晶不是完美的拓扑绝缘体， Dirac表面态构成的费米面不是材料惟一的费米面[100]， Dirac表面态与体态能带在费米能级附近共存(图2(e))， 这是超导自近邻效应的内在要求， 无可避免. 最后， 由于真实材料存在无序、不均、缺陷等不完美因素， 准粒子束缚态会发生耗散.因此， 在多种因素共存的真实材料体系中， 从实验上研究各因素与演生MZM之间的关系， 可以帮助我们更清晰地认识Fe(Te， Se)单晶中涡旋MZM的演生机理， 厘清哪些因素对MZM的形成有直接贡献， 而哪些因素会破坏MZM.

本节将介绍涡旋MZM波函数的空间分布特征[102]以及MZM在不同空间位置和不同温度下的准粒子中毒效应[102]. 在真实的FeTe0.55Se0.45单晶中， MZM由Dirac表面态的超导准粒子产生， 而材料或实验不完美等因素带来的准粒子中毒效应会抑制MZM (基础准粒子中毒效应)， 体态能带提供了额外的费米子浴， 在高温下增强MZM准粒子中毒(额外准粒子中毒效应). 本节最后将对比二维Fu-Kane模型[24]和三维涡线模型[176-178]， 结合实验结果可以发现， 只考虑Dirac表面态的二维Fu-Kane模型可以很好地描述涡旋MZM的极低温行为， 而真实材料的三维特征在高温和空间强不均情况下影响涡旋MZM的存活和演生 .

4.1 涡旋MZM的波函数

MZM波函数具有一定的“空间体积”， 其分布范围由Majorana相干长度决定. 这意味着涡旋MZM的ZBCP不只出现在涡旋中心， 而是在绕涡旋中心一定的空间范围内都可以观测到. STM测量的ZBCP峰强由相应空间位置上的MZM波函数的模平方决定. 在Fu-Kane模型中[24，179]， 均匀超导体的涡旋MZM波函数模方为

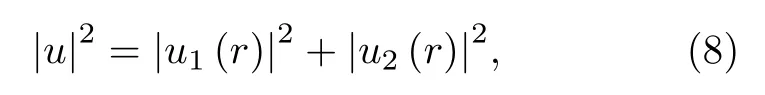
其中

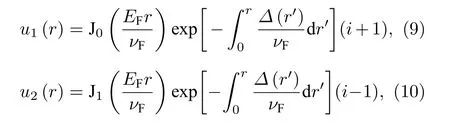
r是离开涡旋中心的距离，Ji(x) 是贝塞尔函数. 将Δ(r) 做阶跃函数近似[102]， 可求得MZM波函数强度的表达式为

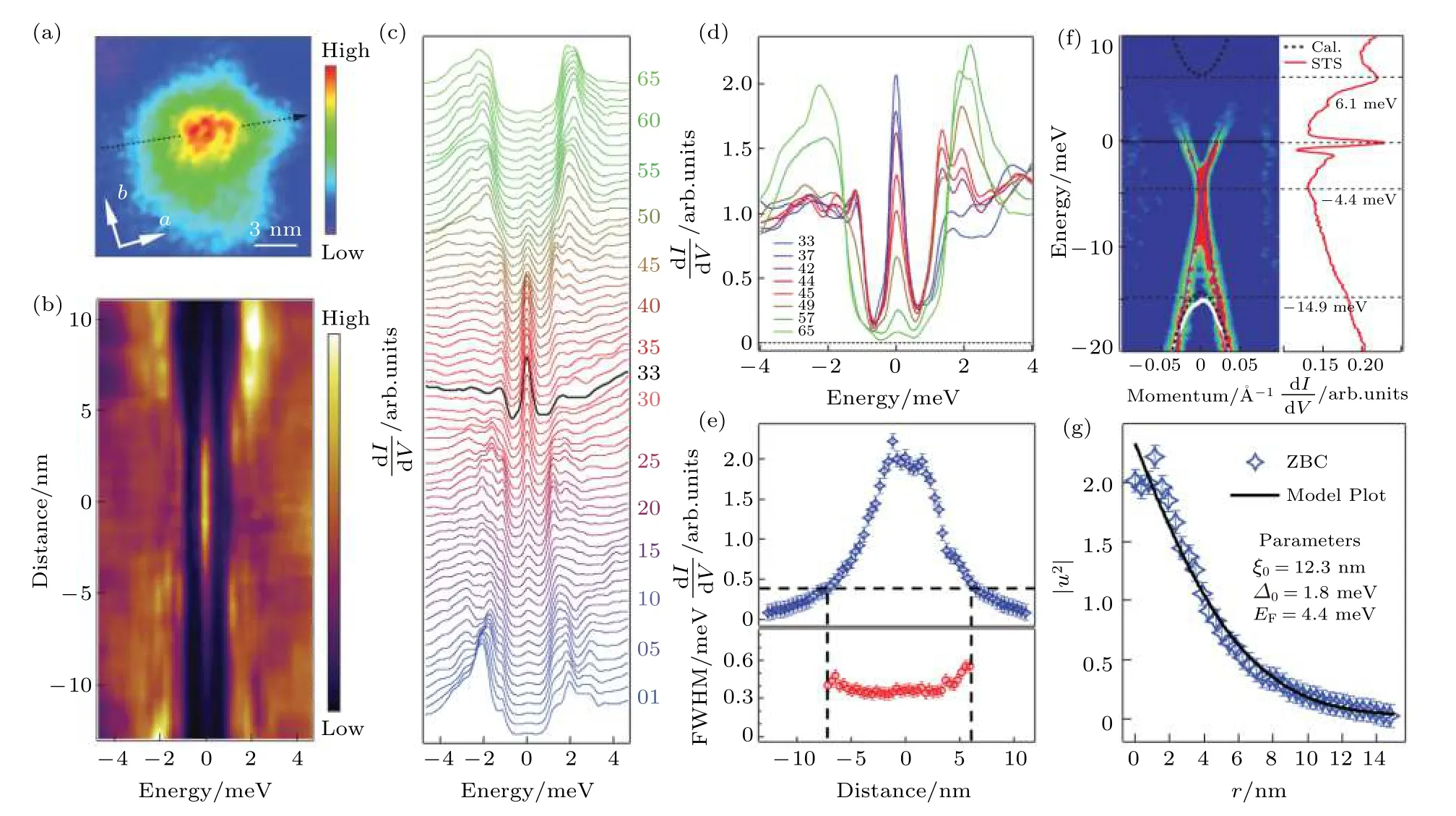
图 7 涡旋MZM的波函数[102] (a)磁通涡旋的零偏压电导绘图; (b)沿着(a)图中黑色点线所示位置测量的dI/dV(r， V)强度分布图; (c)与(b)图对应的dI/dV谱; (d)从(c)图中选取的dI/dV谱的重叠表示; (e)ZBCP的强度(上图)以及FWHM(下图)在空间上的分布; (f)ARPES和STS数据对比， 实验测得Dirac表面态Δ0 = 1.8 meV， EF = 4.4 meV， ξ = νF/Δ0 = 123 Å; (g)实验测量和模型计算的MZM强度空间分布， 参数为(f)图的参数.Fig. 7. The wavefunction of vortex Majorana zero mode[102]: (a) A zero bias conductance map of a topological vortex; (b) a dI/dV(r， V)line-cut intensity plot along the black dashed line indicated in (a); (c) a waterfall-like plot of (b) with 65 spectra; (d) an overlapping display of eight dI/dV spectra selected from (c); (e) spatial dependence of the height (top) and FWHM (bottom) of the ZBCP;(f) comparison between ARPES and STS results， Δ0 = 1.8 meV， EF = 4.4 meV， ξ = νF/Δ0 = 123 Å; (g) comparison between the measured ZBCP peak intensity with a theoretical calculation of MZM spatial profile with the parameters extracted from (f).

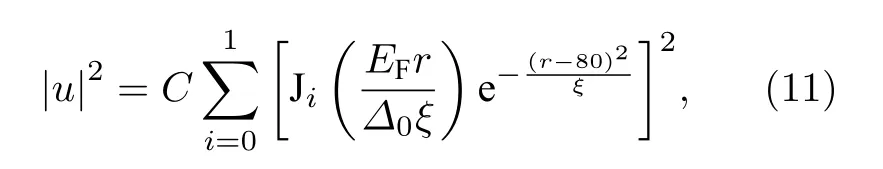
可以证明 Δ (r) 截断阈值的选取不影响结果， 其中C是归一化常数， Δ0是Dirac表面态的原始超导能隙，EF是Dirac表面态的费米能，ξ 是Majorana相干长度.

利用STM测量跨越磁通涡旋的dI/dV谱(图7(a))， 实验发现超导能隙内出现的ZBCP在不同的空间位置上一直保持在零能， 这完全符合MZM的理论预期(图7(b)). 这是目前人们在凝聚态物理系统中获得的最清晰的MZM空间波函数观测结果. 通过仔细分析不同空间位置的dI/dV谱发现， 随着STM测量位置远离涡旋中心， MZM强度逐渐减小(图7(d)). 理论上， MZM零能强度正比于MZM波函数的平方， 如图7(e)所示， 实验提取了MZM零能强度在空间上的分布. 为了确定Dirac表面态的真实参数， STM实验测量了磁通涡旋中心宽能量范围的dI/dV谱， 并将其与ARPES测量的Dirac表面态进行对比(图7(f)).STS谱在6.1和—14.9 meV处的特征分别与ARPES测得的导带底和价带顶的能量位置符合得很好. STS谱在—4.4 meV处呈现线性凹陷行为， 这是Dirac点的态密度特征[180]， 同时ARPES实验在—4.4 meV附近也观测到了拓扑表面态的Dirac点. 结合ARPES和STM的实验观测并作简单推算， 可以得到Dirac表面态的实验参数如下: Δ0=1.8 meV， EF= 4.4 meV， ξ = νF/Δ0= 123 Å. 将这些参数代入Fu-Kane模型导出的MZM波函数(11)式中， 经过必要的归一化处理， 研究发现使用Dirac表面态的真实实验参数， Fu-Kane模型可以完美重现STM实验观测到的MZM峰强空间分布特征(图7(g)).

图7的实验结果表明， FeTe0.55Se0.45单晶的Dirac表面态催生了涡旋MZM. 虽然在真实体系中磁通以一维涡线的形式穿过整个三维体材料(磁通涡线具有kz一维色散). 但是， 在涡旋MZM出现的前提下， 二维的Fu-Kane近似模型对于分析涡旋MZM的极低温行为依然有效， 这时可以把FeTe0.55Se0.45单晶样品中演生的涡旋MZM看作是二维超导拓扑表面态的涡旋点缺陷上的MZM.本文将在4.3节和第7节中介绍真实三维材料中的具有一维能谱色散的涡线， 涡线的参与会影响表面涡旋中MZM的演生.

4.2 涡旋MZM的准粒子中毒

在绝对零度， 完美s波超导体中的所有导电电子都组成库伯对， 超导准粒子浓度为零[181]， 随着温度升高， s波超导体能隙中出现热激发准粒子的占据. 在有限温度下， 其热平衡浓度为

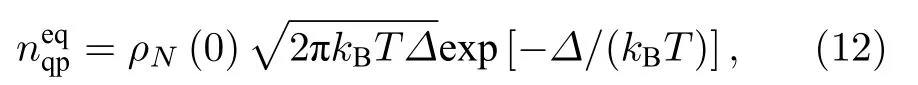
其 中 ρN(0) 为 正 常 态 费 米 能 级 处 的 态 密 度. neqqp对应的准粒子寿命可以按照下式估计:

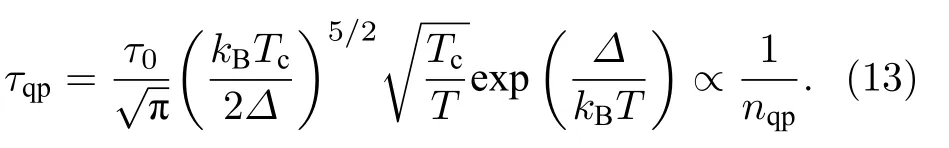
然而实验发现， 材料中的超导准粒子浓度往往远远超过(12)式所预期的热平衡值， 这造成了超导准粒子寿命缩短[182，183]. 这种来源尚不完全明确的非平衡超导准粒子占据对实验预期有严重干扰， 因此被称为准粒子中毒[182-190]. 超导体准粒子中毒效应的强弱可以由超导能隙的“软硬”来表征， 越“硬”的超导能隙在态密度谱上具有越陡峭的能隙边和更小的能隙内态密度， 这代表未配对的超导准粒子越少.

准粒子中毒效应本质上为相干量子态提供了一个可以耦合的费米子池， 超导能隙内的量子束缚态与费米子池的耦合是一个量子耗散的过程， 这使得量子束缚态寿命降低， 在态密度谱上表现为峰宽变大， 峰强减小[184-187]. 对于MZM构成的系统，量子比特由相同费米子宇称的量子态构成，Majorana量子比特只对保持费米子宇称的扰动免疫， 而准粒子中毒效应会改变MZM系统的费米子宇称， 破坏Majorana量子比特， 造成信息丢失， 因此， 所有的量子比特操作都必须在准粒子中毒定义的MZM寿命之内完成[184-190]. 同时， 从MZM实验观测的角度看， 准粒子中毒效应会降低MZM强度、增大能量展宽， 导致MZM实验信号消失. 准粒子中毒效应是MZM的主要破坏因素， 也是发展拓扑量子计算的主要障碍之一. 在FeTe0.55Se0.45单晶中研究涡旋MZM的准粒子中毒效应， 可以为铁基超导体中MZM的演生机理以及潜在应用提供宝贵信息.

首先， 低温(0.55 K)实验研究了涡旋MZM在不同空间位置上的基础准粒子中毒效应. 如图8(a)所示， 实验选取三个磁通涡旋， 分别测量了涡旋中心(红色曲线)和涡旋边缘(黑色曲线)的dI/dV谱. dI/dV谱在涡旋中心都存在尖锐的ZBCP， 在涡旋边缘谱形恢复超导能隙特征. 涡旋附近准粒子中毒效应的强弱可以用涡旋边缘谱的能隙内态密度来表征， 定义涡旋边缘谱—1—1 meV范围内的微分电导积分值为涡旋位置的准粒子背景，作为准粒子中毒效应的定量衡量. 通过同时分析涡旋中心ZBCP的FWHM和涡旋边缘的准粒子背景， 实验发现超导准粒子中毒效应越强的空间位置上出现的MZM具有越大的能量展宽， 即具有更短的准粒子寿命(图8(a)右下图). 准粒子中毒效应导致实验观测到某些涡旋MZM具有远大于系统能量分辨率的ZBCP展宽. 在准粒子中毒效应很弱的空间位置出现的涡旋MZM的能量展宽接近系统能量分辨率极限. 涡旋MZM的准粒子中毒强度存在明显的空间不均性， 这应该与FeTe0.55Se0.45单晶样品的本征不均性有关(详见6.3节、第7节).

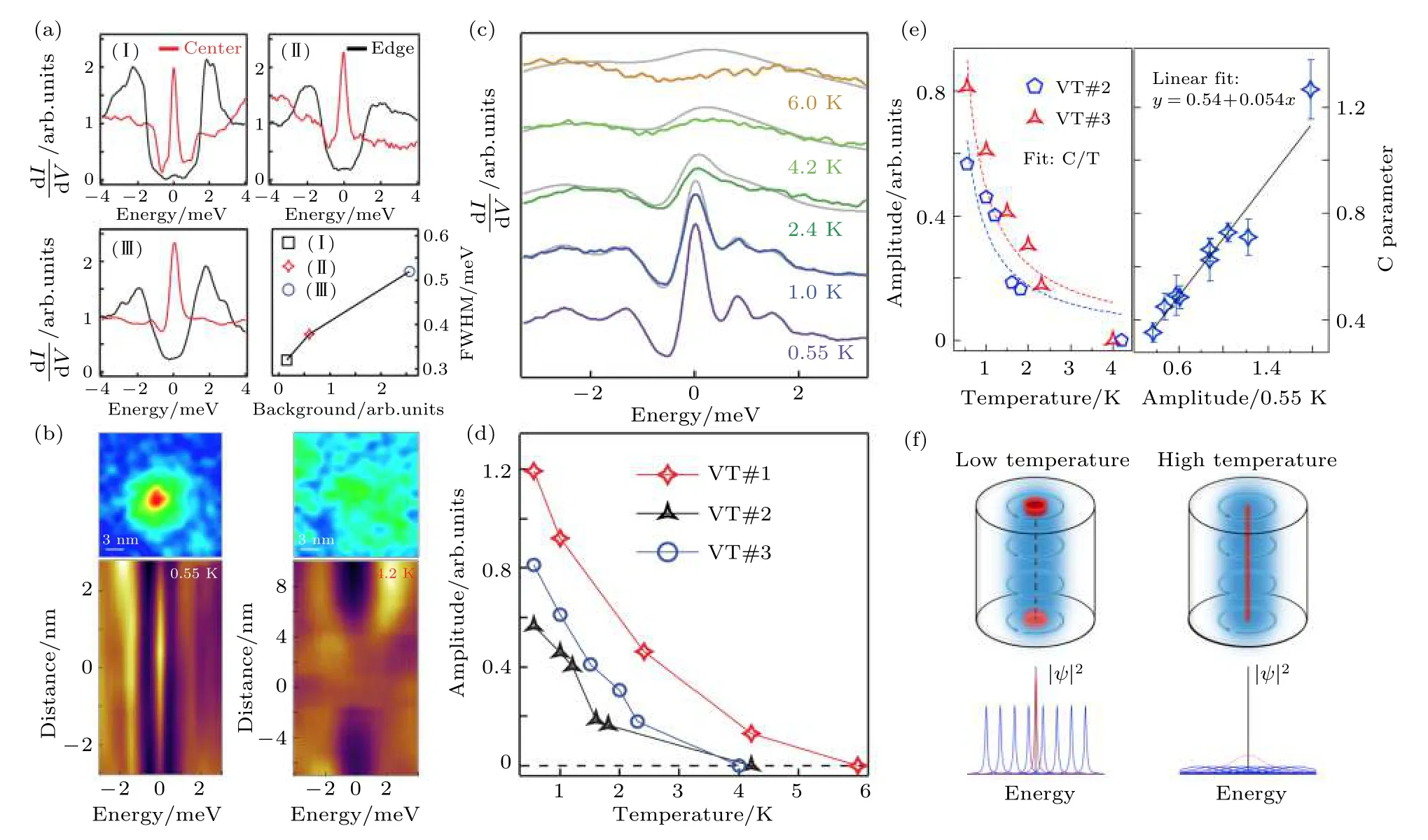
图 8 涡旋MZM的准粒子中毒效应[102] (a)三个不同磁通涡旋中测量的涡旋中心谱和边缘谱， Background定义为涡旋边缘谱—1—1 meV的积分值， 显然， 超导能隙越“软”， 涡旋中心的ZBCP峰宽越大; (b) 0.55 K (左侧)和4.2 K (右侧)下测量的涡旋束缚态; (c)涡旋MZM的变温实验， 其中灰色曲线为最低温曲线的数值温度卷积; (d)涡旋MZM振幅随温度的变化， 振幅定义为ZBCP的峰谷差; (e)降低准粒子中毒有望提高MZM的存活温度， 左图: 使用C/T拟合MZM振幅随温度的变化关系， C与涡旋MZM的存活温度正相关; 右图: 对9个涡旋MZM变温实验的总结， 0.55 K下振幅越大的MZM可以在更高的温度下存活; (f)涡旋MZM随温度变化行为的合理机制， 红色曲线为涡旋MZM， 蓝色曲线为体能带催生的体态涡旋束缚态的示意图Fig. 8. Quasiparticle poisoning of vortex Majorana zero modes[102]: (a) Three vortex Majorana zero modes measured on different locations， the FWHM of ZBCP at the center of the vortex core is larger when the SC gap around the vortex core is softer; (b) a zero bias conductance map of vortex and line-cut intensity plot of Majorana zero modes measured under 0.55 K (left) and 4.2 K (right)，respectively; (c) temperature evolution of ZBCPs in a vortex core. The gray curves are numerically broadened 0.55 K data at each temperature; (d) amplitude of the ZBCPs of three vortex MZMs under different temperatures. The amplitude is defined as the peak-valley difference of the ZBCP; (e) left panel: C/T fitting of amplitude of Majorana ZBCPs under different temperatures. Right panel: summary on several temperature evolution measurements; (f) schematic explanation of the temperature effect on Majorana ZBCPs. The red line is the vortex MZM and the blue line is the bound state of body votex.

接下来， 实验关注选定的涡旋MZM， 研究了升高温度引入的额外准粒子中毒效应. 为了最大程度减小涡旋蠕变带来的影响[191，192]， 实验上采取缓慢升温的方式， 使得磁通涡旋不随变温而移动， 确保变温实验研究的是同一个涡旋MZM. 图8(b)左右两侧分别是在0.55和4.20 K下测量的涡旋零偏压电导绘图以及跨越涡旋中心的dI/dV(r， V)强度分布图. 出人意料的是涡旋MZM特征在4.2 K下便完全消失了， 在2.2节中， ARPES实验表明Dirac表面态的超导能隙在14.5 K左右关闭， 而这里STM实验观测到的涡旋MZM消失温度远低于Dirac表面态能隙关闭温度， 这一行为不能用Fu-Kane近似模型进行解释. 结合我们在4.1节中利用Fu-Kane模型导出的涡旋MZM波函数((11)式)可以看到， 涡旋MZM的强度只通过超导能隙接受温度的调制. 由于常规超导体的能隙在Tc/2 (约8 K)以下基本保持不变[181]， 因此理论预期在8 K以下， FeTe0.55Se0.45单晶中涡旋MZM的温度演化应该遵循费米-狄拉克函数卷积规律. 然而图8(b)的数据显示MZM在4.2 K时就过早消失， 这表明材料中存在其他抑制机制加速了MZM的升温破坏. 为了深入研究MZM温度演化行为的微观机制， 图8(c)绘制了涡旋中心ZBCP的变温曲线. MZM的峰宽由隧穿耦合强度、温度展宽、仪器分辨率以及基础准粒子中毒效应共同决定. 改变实验温度并保持其他实验条件不变时， 隧穿耦合强度和仪器分辨率保持稳定， 如果准粒子中毒效应也保持恒定， 那么在 Tc/2 以下MZM的dI/dV谱可以由最低温dI/dV谱卷积费米-狄拉克函数得到(图8(c)中灰色曲线). 然而数值卷积显示， 在升高温度的情况下MZM的峰强被过度压制， 峰强随温度的衰减超越了费米-狄拉克函数的影响程度. 这一现象在9个不同的涡旋MZM上得到了很好的重复. 实验提取了不同温度下的ZBCP振幅， 并将其中三个涡旋MZM的情况绘制在图8(d)中. 其中ZBCP振幅定义为ZBCP的峰-谷强度差， 非零的ZBCP振幅是观测MZM的必要条件. 显然， 大多数涡旋MZM的ZBCP振幅在3 K左右消失， 这远远低于Dirac表面态超导能隙的关闭温度. 仔细考察体能带的参数可以发现， MZM的消失温度与体能带相关的一维涡线束缚态能隙(δ)接近[99]， δ = (Δ2/EF)Bulk≈(kBT)|T=3K. 这一结果表明， 涡旋MZM随着温度升高表现出的过度压制行为与体态能带密切相关， 这是FeTe0.55Se0.45单晶的三维性导致的.在实际实验中， 磁通涡线沿着晶格c轴方向贯穿整个材料， 一维涡线体内的束缚态由体态能带演生(涡线末端的涡旋束缚态与表面态有关).FeTe0.55Se0.45单晶的能带参数测量表明Dirac表面态比体态能带具有更大的Δ2/EF， 温度效应将主要激发体态超导准粒子. 在极低温度下(kBT≪δ)，一维涡线对于超导准粒子绝缘， 涡线末端由表面Dirac电子产生的涡旋MZM可以近似看作是孤立二维拓扑超导系统点缺陷上的MZM， 这时可以忽略材料的三维特征. 但是严格地讲， 样品表面的涡旋MZM是一维涡线的末端束缚态， 在样品垂直方向上被一维涡线体内的准粒子能隙(δ)保护. 可以证明， MZM波函数沿着c方向的特征局域长度反比于δ (图8(f)左图)[176]. 随着温度升高， 一维涡线体内的热平衡超导准粒子遵循指数增加规律(活化行为). 这些由热激发产生的体内超导准粒子与束缚在材料表面的涡旋MZM混合， 扮演了额外费米子池的角色， 提供了准粒子中毒的额外来源， 这使得准粒子中毒效应随着温度上升而加重， 造成涡旋MZM的过度压制行为(图8(f)右图). 当kBT ≈δ时， 从体内产生的热激发准粒子会与表面的涡旋MZM强烈混合， 涡旋MZM的波函数被拉入体内，甚至与涡线另外一端的MZM相遇湮灭.

最后， 图8(e)总结了9次涡旋MZM变温实验，将测量得到的ZBCP振幅用 C/T 进行拟合(理论依据详见第5节)， 提取出的C参量与MZM的最高存活温度正相关. 研究发现， 0.55 K下具有较大ZBCP振幅的涡旋MZM有较大的C参量，这暗示升温导致的额外准粒子中毒效应可能在空间上分布均匀， 而空间分布不均的基础准粒子中毒效应(图8(a))改变了准粒子中毒效应的起始点，从而影响了MZM的最高存活温度. 减小基础准粒子 中毒效应有助于实现高温MZM.

4.3 二维Fu-Kane模型与三维涡线模型中的MZM

从前面的介绍已经知道， 在FeTe0.55Se0.45单晶中， Dirac表面态是演生涡旋MZM的直接贡献者， 而准粒子中毒效应会破坏MZM. 体能带在高温下提供额外准粒子中毒效应， 是MZM的“毁灭者”. 在极低温下， 对于已知存在MZM的涡旋， 真实材料的三维特征可以被忽略， MZM的低温行为可以被二维Fu-Kane模型很好地描述. 然而， 真实材料的三维特征， 特别是Dirac表面态与体态能带在费米能级附近共存的事实， 确实会对FeTe0.55Se0.45单晶表面上的涡旋MZM演生机制产生影响， 因此， 研究更为细节的三维理论模型不仅可以拓展Fu-Kane模型， 而且可以为真实材料中演生的涡旋MZM提供更多信息.

实际上， 在Fu-Kane模型提出不久人们就意识到多数拓扑绝缘体的本征化学势并不位于体态的绝缘体能隙内， 拓扑绝缘体的体态不再是绝缘态， 而是金属态[25]. 这自然带来一个问题——当体态导电的拓扑绝缘体引入超导配对时， 表面磁通涡旋中是否仍然存在MZM[176，193]? 很快， 理论物理学家以电子掺杂的Bi2Se3为载体建立了三维模型[176-178]， 研究了体态不绝缘时沿c方向贯穿体材料的一维磁通涡线的拓扑相变行为. 三维涡线模型将体态能带放入涡旋BdG方程中， 通过求解BdG方程可以得到体态能带导致的、具有一维色散的涡线束缚态[176]. 如图9所示， 当化学势位于体态能带的绝缘体能隙中时(μ ＜ |mG|)， 一维涡线对准粒子完全绝缘， 不存在涡线束缚态. 当化学势升高并触及体态能带时(μ = |mG|)， 具有一维色散的涡线束缚态出现， 它们的不同能级之间具有极小的能量间隔(δ ≈ (Δ2/EF)Bulk). 这时涡线内部在极低温下仍然绝缘. 随着化学势继续升高， 涡线束缚态能级间隔持续变小， 可以证明， 当体态能带Berry相位达到π时， 体态涡线束缚态移动到零能，在kz一维方向上呈无能隙线性色散分布(μ = μc)，这时磁通涡旋发生拓扑相变. 如果继续增加化学势， 涡线束缚态将重新打开能隙， 磁通涡线进入不同的拓扑相.

通过计算体能带的Berry相位或者直接计算高对称点的涡线束缚态， 三维涡线模型可以有效确定涡线拓扑相变发生的位置[176]， 然而三维涡线模型本身并不能确定相变前后哪一侧是拓扑非平庸的， 这一鉴定的实现需要利用体态能带重新计算相变前后的拓扑不变量. 换句话说， Dirac表面态的存在与否决定了相变前后的哪个相是拓扑非平庸的， 这恰恰是二维Fu-Kane模型告诉我们的信息.为了将这一点阐述得更加明确， 本文下面利用这两种模型分别讨论涡旋MZM在超导的三维拓扑绝缘体和超导的普通绝缘体中的行为. 1)正常态是拓扑绝缘体的情况. Fu-Kane模型中的涡旋MZM可以在任意化学势下存在. 改变Dirac表面态的化学势会减小束缚态的拓扑能隙但不能使涡旋MZM消失. 而在三维涡线模型中， 化学势位于Dirac点时涡旋中存在MZM. 随着化学势的升高，体态能带参与进来， 涡线体内出现能隙微小的束缚态， 这使得材料表面上的涡旋MZM波函数向体内延伸， 直至化学势跨越拓扑相变点， 涡旋MZM消失. 在三维涡线模型中， 涡旋MZM只能在Dirac点附近的有限化学势范围内存在. 2)正常态是普通绝缘体的情况. 这时Fu-Kane模型是真空模型，任何化学势下都不存在涡旋MZM. 在三维涡线模型中， 零化学势附近不存在MZM， 但是升高化学势会发生涡线束缚态的拓扑相变. 随着化学势的改变， 体态能带的Berry相位跨越π， 涡旋MZM出现在样品表面[176].

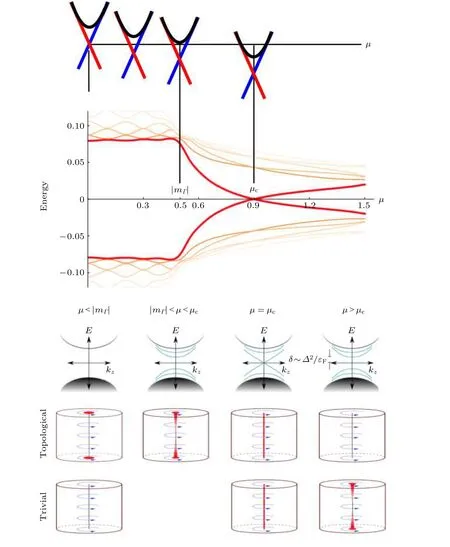
图 9 三维涡线模型中的涡线拓扑相变. 第一行: 拓扑材料费米面随化学势的变化. 第二行: kz = 0处的低能涡线束缚态随化学势的变化， 其中红色曲线代表最低能的涡线束缚态. μ ＜ |mG|时， 费米能级位于体态能隙内， μ = |mG|时费米能级位于导带底／价带顶. μ = μc时， kz = 0处的涡线束缚态发生拓扑能带反转， 涡线拓扑相变发生. 第三行: 不同化学势下涡线束缚态的kz 色散. 第四行: 当材料为拓扑绝缘体时， 表面MZM随化学势的演化. 第五行: 当材料为普通绝缘体时， 表面MZM随化学势的演化. 本图改编自文献[176]， 部分内容为原创Fig. 9. Topological vortex phase transition in the three-dimensional vortex line model. The first line: Evolution of the band structure of a topological material by tuning the chemical potentials. The second line: Evolution of the low energy vortex bound state at kz = 0 under different chemical potentials. The third line: The kz dispersion of low energy vortex bound states. The fourth and fifth line: evolution of vortex Majorana zero modes under different chemical potentials in topological insulator and normal insulators， respectively. This figure is adapeted from Ref. [176]， some features are added by us.

可见， Fu-Kane模型是研究涡旋MZM的核心模型， 三维涡线模型是对Fu-Kane模型的拓展. 真实材料的三维特征不仅引入了额外准粒子中毒效应， 而且在改变化学势的条件下引入了涡线拓扑相变， 相变前后涡旋MZM产生或消失. 三维涡线模型中处于拓扑相的磁通涡线可以看作是一维的Class-D拓扑超导体[194-197]. 三维涡线模型对理解束缚态拓扑相变具有深刻意义， 现已被推广到更具体的情况， 比如Fe(Te， Se)单晶中的涡线拓扑相变[198]， 拓扑体能带与平庸体能带耦合时的涡线相变(拓扑非平庸相区变形但仍需包括表面态的Dirac点)[199]， 塞曼(Zeeman)耦合驱动的涡线拓扑相变[200]， 正常态是弱拓扑绝缘体[201]以及Dirac半金属[202，203]时的涡线拓扑相变等等.

本节介绍了真实三维材料中涡旋MZM的演生机制， 详细解答了为什么Fe(Te， Se)单晶样品中存在涡旋MZM. 可以看到， Dirac表面态是演生涡旋MZM的主要贡献者， 在MZM出现的前提下， Fu-Kane模型可以很好地描述涡旋MZM的极低温行为， 这时材料的三维特性可以被忽略. 准粒子中毒效应会破坏涡旋MZM， 高温下体态能带会引入额外准粒子中毒效应， 加速涡旋MZM的消失. 体态能带的存在还会影响涡旋MZM的演生，当化学势存在很强的空间涨落时， 部分空间位置可以跨越相变点， 此处的磁通涡旋中不能演生MZM.在理解了FeTe0.55Se0.45单晶演生涡旋MZM的机理之后， 本文下面将聚焦涡旋MZM的基本性质.

5 测量涡旋MZM的Majorana本质:粒子-空穴等价性

产生湮灭算符的自共轭性质( γ†=γ )是MZM的本质性质， 也是MZM获得“Majorana”命名的原因. MZM可以用复费米子算符( c†， c)写成 Bogoliubov准粒子的形式， 即

MZM的本质性质(Majorana对称性)使得MZM的电子部分和空穴部分波函数等价(u*= v)，电子-空穴等价性是MZM的Majorana本质的直接体现[1-8]. 本节将结合Law-Lee-Ng理论[204]介绍 Majorana准粒子电子-空穴等价性导致的共振Andreev反射， 这使得Majorana准粒子获得本征共振量子电导(2e2/h)， 在理想实验状况下MZM的电导值对隧穿耦合强度的变化免疫. 文献[105]通过变耦合强度STM谱的方法， 在FeTe0.55Se0.45单晶的涡旋MZM上观测到对隧道结变化免疫的电导平台， 实验发现电导平台行为是MZM所独有的， 在有限能量CdGM态、零场零偏压以及超导能隙外的连续态上都不存在电导平台行为， 最重要的是， STM实验在其中一个涡旋MZM上测量到了2e2/h量子化的Majorana电导平台， 这一结果强烈暗示实验成功观测到了MZM导致的共振Andreev反射(MIRAR)， 这是涡旋MZM的Majorana本质的直接体现.

5.1 Majorana量子电导理论: 共振Andreev反射

MIRAR可以看作是经典共振隧穿[205-207]的超导版本. 在半导体异质结中， 通过能带工程的方法可以构造双势垒隧穿结构. 如图10(a)所示， 利用AlGaAs导带底双势垒构造的量子阱中存在量子化的准束缚态， 当电子从左向右跨越量子阱隧穿时， 如果左右两侧的势垒相同， 则电子隧穿透射系数为

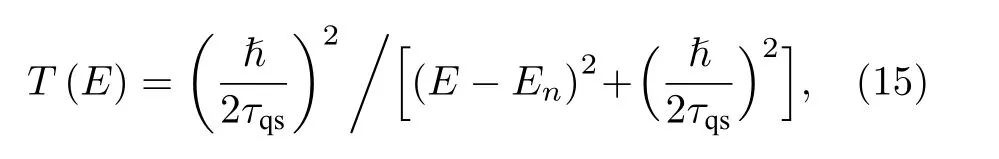
其中 τqs为准束缚态的准粒子寿命，En为准束缚态的能量. 可见当入射电子能量恰好与准束缚态能级对齐时， 电子发生无损耗完美透射. 这一现象与光学Fabry-Perot腔的共振透射具有类似的机理， 电子波在量子阱的两个势垒之间发生多重反射并相互干涉， 当电子能量与 En对齐时， 电子波发生相长干涉使得反射电子波被抵消， 透射系数为1， 且透射系数不受势垒大小的影响. 经典共振隧穿的波函数如图10(b)所示. 经典共振隧穿还可以通过两个相同针尖的跨越隧穿来实现(图10(c))， 当两针尖与准束缚态之间的电子跃迁几率幅相等时(t1= t2)，共振隧穿发生. 值得注意的是， 隧穿耦合强度( Gt)与跃迁几率幅(t )之间的关系为 Gt= 2πρ0|t|2， 其中ρ0是与耦合相关的态密度. 对于相同针尖的跨越隧穿， t相等时 Gt也相等.

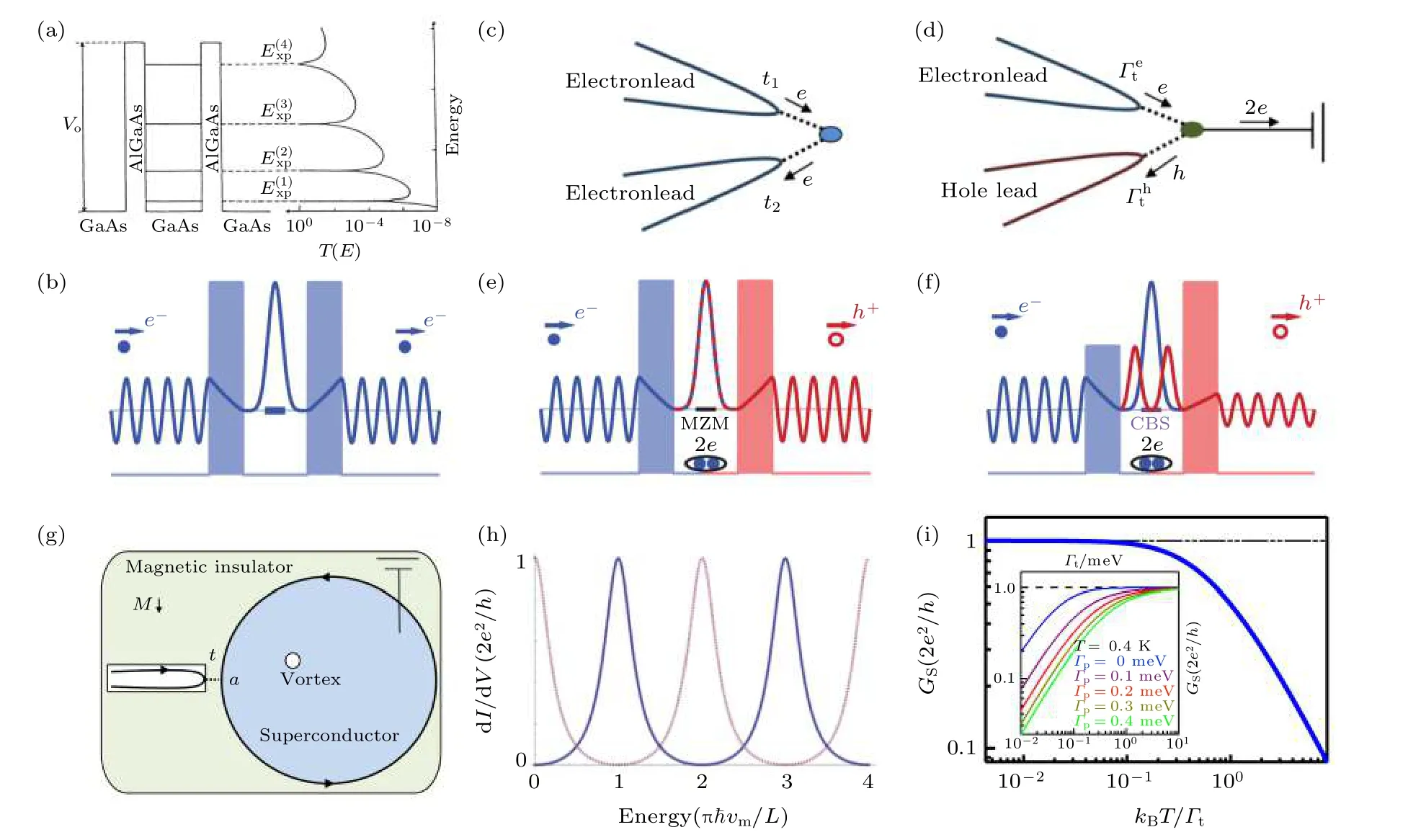
图 10 共振Andreev反射与MZM本征量子电导 (a)半导体异质结中的经典共振隧穿[207]， 隧穿电子能量与双势垒准束缚态能量一致时透射系数为1; (b)经典共振隧穿的电子波函数[105]; (c)经典共振隧穿的替代实验构型: 两针尖跨越隧穿[204]， 实现经典共振隧穿的必要条件是两针尖与准束缚态之间的跃迁几率幅相等(t1 = t2); (d) MZM导致的MIRAR[204]. 与经典共振隧穿不同，MIRAR是电子和空穴希尔伯特空间的跨越共振隧穿， 因为入射电子和反射空穴在同一个物理针尖上完成， 因此空穴和电子的跃迁几率幅相等(th = te)， MZM对称性保证入射和反射的隧穿耦合强度相等 ( Γte=Γth; Gt = 2πρ0|t|2， 其中 ρ0是有关的态密度)，实现共振条件; (e) MZM参与的Andreev反射的空间波函数， 其中蓝色代表电子部分， 红色代表空穴部分[105]; (f) CdGM束缚态参与的Andreev反射的空间波函数[105]; (g) Law-Lee-Ng理论揭示Majorana模式的本征共振电导[204]; (h)理论计算的Majorana量子电导为2e2/h， 其中蓝色曲线对应(g)中超导体中存在偶数个涡旋的情况， 红色曲线是存在奇数个涡旋的情况[204]; (i)Majorana量子电导的有限温标度行为以及准粒子中毒效应对量子电导的影响Fig. 10. Resonance Andreev reflection induced Majorana quantum conductance: (a) Conventional electron resonance tunneling in a semiconductor heterostructure[207]; (b) the wavefucntion of conventional resonance tunneling[105]; (c) two tips cross-tunneling can be regarded as a replacement of semiconductor heterostructure for realizing semiconductor heterostructure under the condition of equal hopping amplitude around the two tips (t1 = t2)[204]; (d) the Majorana induced resonance Andreev reflection (MIRAR) can be regarded as a superconducting version of the conventional resonance tunneling in the particle-hole Hilbert space. Here a single electrode plays both roles of electron and hole electrode[204]. Due to the particle-hole equivalence property， Majorana modes couple to the incident electron and reflected hole with equal tunneling coupling strength， which satisfies the resonant condition ( Γte=Γth ; Gt =2πρ0|t|2， ρ0 being the related density of states); (e)， (f) the wavefucntion of Andreev reflection mediated by MZM and a conventional Andreev bound states， respectively[105]; (g) the material setup used in Law-Lee-Ng model[204]; (h) the theoretical calculated resonance quantum conductance of Majorana modes[204]; (i) theoretical calculated Majorana conductance under finite temperature and poisoning rate.

如果将经典共振隧穿出射部分的电子换成空穴， 出射部分的电子势垒也换成空穴势垒， 那么这一过程就变为共振Andreev反射(图10(d))[204].单个针尖既可以充当入射电子极又可以充当反射空穴极， 这自然保证了Andreev反射过程中te= th.为了满足电子-空穴隧穿共振条件( Gte=Gth)， 还需要使Andreev过程的电子和空穴部分波函数相等(ρe= ρh). MZM的Majorana对称性自然满足了共振Andreev反射的这一需求(图10(e)). 在绝对零温和无耗散的情况下， 单针尖与MZM隧穿耦合， 电子通过MZM发生的Andreev反射是共振过程， Majorana电导与隧穿耦合强度无关. 而普通Andreev束缚态(比如磁通涡旋中有限能量的CdGM束缚态)的波函数电子和空穴部分不相等，导致电子和空穴极的隧穿耦合强度不等( Gte／=Gth)，不满足共振Andreev反射的条件(图10(f)).

Law-Lee-Ng理论利用Fu-Kane模型中的Majorana磁性边界态[56，57]详细计算了MIRAR的量子电导. 如图10(g)所示， 在拓扑绝缘体表面上覆盖超导体岛， 岛外的区域则被垂直自发磁化的磁性绝缘体覆盖， 因此在超导岛下方， Dirac表面态打开等效无自旋手性p波超导能隙， 而在岛外， Dirac表面态打开磁性Zeeman能隙(EZ=gμBM)， 其中g是朗德因子， μB是玻尔磁矩， M是有效磁化强度. 当时， 一维手性Majorana磁性边界态出现在超导岛的边界上. 利用简单的固体物理知识可知， 一维手性Majorana磁性边界态的量子化Majorana能级为

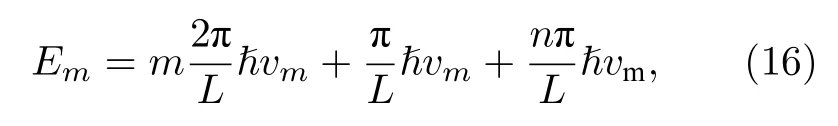
对应的Majorana量子化动量为

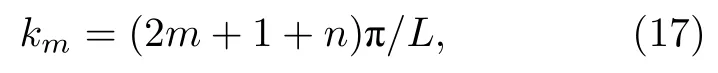
其中m是任意整数， L是超导岛的周长，vm是Majorana磁性边界态的费米速度，n 是超导岛内量子化磁通涡旋的个数. (16)式和(17)式中的第一项来源于周期性边界条件， 第二项是Dirac表面态自旋Berry相位的贡献， 第三项来源于超导磁通涡旋. Law-Lee-Ng理论将单个金属电极与Majorana磁性边界态在a点进行隧穿耦合(图10(g))， 耦合几率幅为t. 系统的总哈密顿量为 HLLN=HL+HM+HT， 式中金属电极部分哈密顿量写为

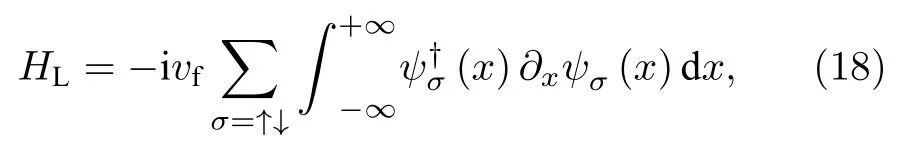
其中 vf是电子的费米速度，ψσ(x) 是费米子场算符.M ajorana部分哈密顿量写为

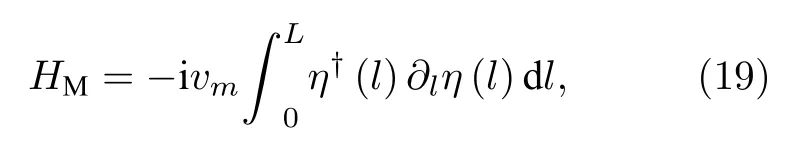
耦合部分哈密顿量写为

其中 η (a) 是在耦合点的Majorana场算符， f和g 是模为1的复数. 对费米子场做如下变换:

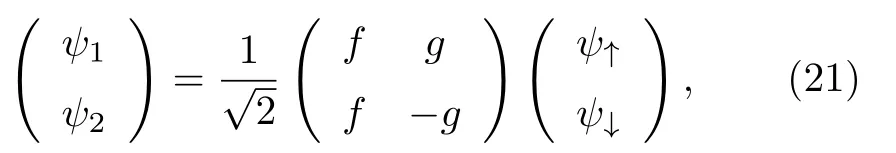
系统哈密顿量可以简化为 HL′LN=HL′+HM+HT′，其 中

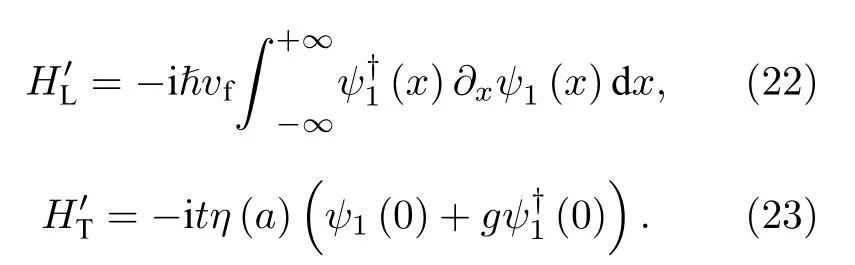
可见， 变换后的费米子场只有一种自旋( ψ1)参与MZM的Andreev反射， 而另外一种自旋( ψ2)与MZM完全脱耦[204，208-211]. 参与Andreev过程的入射电子和反射空穴自旋相同， 分别将其记为.

电子-空穴散射过程可以写成S-矩阵的形式，

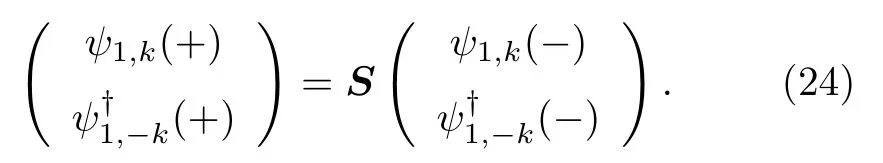
利用 HL′LN计算得到的Majorana系统的S-矩阵为

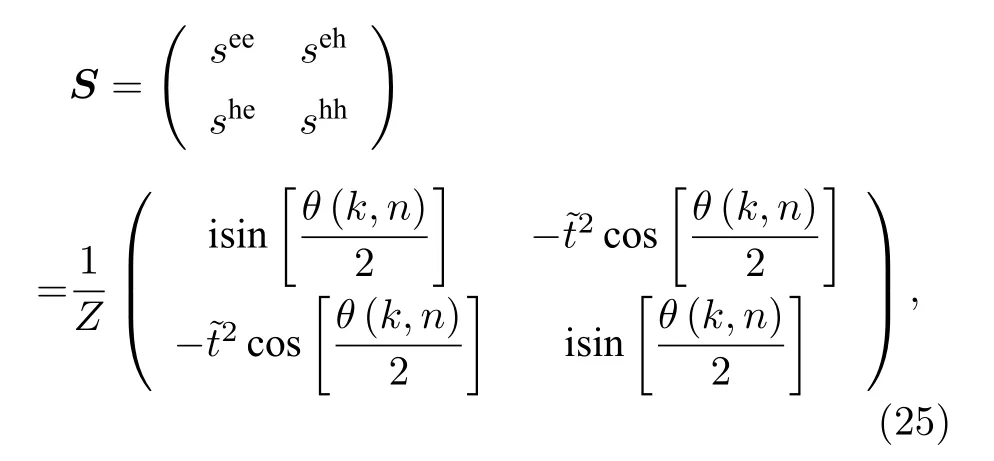
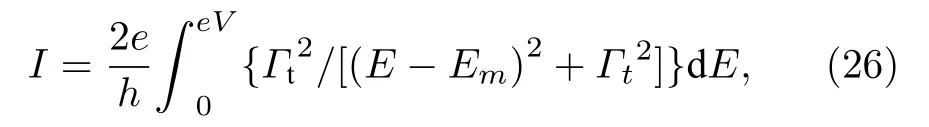
其中 Gt=2t2ℏvm/L ， 是隧穿耦合强度. 对应的微分电 导为

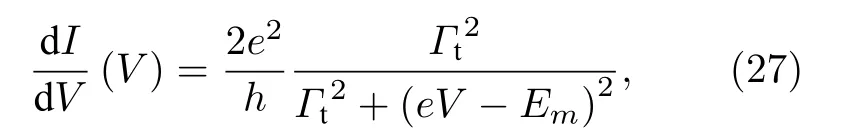
于是Law-Lee-Ng理论导出了Majorana共振量子电导， 其大小为 2 e2/h (图10(h)). 需要指出的是，MIRAR和Majorana共振量子电导根植于粒子-空穴等价性， 是Majorana准粒子拥有的普遍性质，这一结果的导出不依赖于模型中Majorana准粒子的形式(边缘模[204]或零能模[212-214])、理论方法(S矩阵[204，214]或格林函数[212])、以及耦合程度(隧穿[204，212]或量子弹道[213])的选择， 因此可以被当作Majorana本质性质的直接体现， 领域内一些物理学家甚至将其看作鉴定Majorana准粒子的决定性证据.

Law-Lee-Ng理论考虑了系统在绝对零温和无耗散情况下的Majorana电导， 这时涡旋MZM的零偏压电导在任意的隧穿耦合强度下都为共振量子值(2e2/h)， 在变隧穿耦合强度条件下测量涡旋MZM电导， 呈现量子化电导平台行为. 然而现实总是不完美的， 通常实验测量到的MZM零偏压电导往往远小于2e2/h[33]， 因此研究非完美情况下(有限温度、存在耗散)的Majorana电导行为显得十分必要[212-218]. 本节下面将讨论涡旋MZM在有限温度和存在耗散(考虑准粒子中毒效应)的情况下的零偏压(共振能量)电导行为. 首先考察无耗散有限温系统的Majorana电导. 利用Law-Lee-Ng理论的结果可以导出有限温度下MZM零偏压电导为

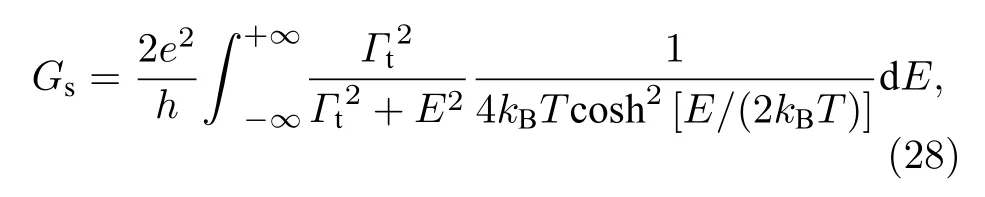
利用数值计算可以发现MZM零偏压电导满足kBT/Gt的 通 用 标 度 行 为(图10(i))[215-217]， 即， 其中 f (x) 为标度函数. 这表明在无耗散系统中只有当隧穿耦合强度远大于温度展宽时， Majorana共振量子电导才可以被观测到.

下面讨论存在准粒子中毒时的Majorana电导行为. 本文在4.2节中已经详细介绍了准粒子中毒效应减小MZM电导信号的现象. 在零温下， 考虑准粒子中毒的MZM电导变为

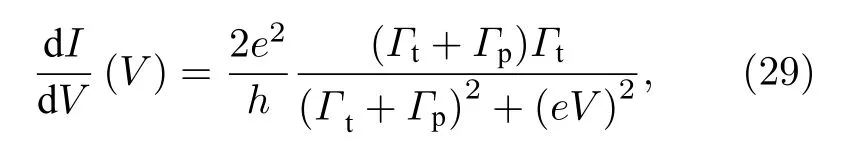
其中Gp= 2πρp|tp|2是费米子池与MZM的耦合强度[186]. 可见在准粒子中毒效应的作用下， MZM的零偏压电导变为量子电导的 Gt/(Gt+Gp) . 与无耗散系统中使用的方法相同， 有耗散系统MZM电导在有限温下的行为可以通过零温MZM电导卷积费米-狄拉克函数的导数( d fFD/dE )获得. 通过数值计算不难发现， MZM零偏压电导在耗散系统中不再遵循 kBT/Gt标度行为. 本文在图10(i)的插图中计算了0.4 K、不同耗散条件下的零偏压电导随隧穿耦合强度的变化， 不难发现耗散导致GS减小，但在 Gt≫Gp时GS仍趋于量子电导. 综上所述，MZM的峰宽主要由温度展宽(3.5 kBT )、耗散以及Majorana本征隧穿耦合展宽(2(Gp+ Gt))决定. 只有当 Gt远大于 kBT和 Gp时才能观测到MZM量子化电导平台.

5.2 涡旋MZM零能电导平台的实验观测

FeTe0.55Se0.45单晶具有很大的拓扑能隙(Δ2/EF)， 当下STM的能量分辨率足以将涡旋MZM与其他平庸束缚态进行清晰分辨， 在实验上获得孤立的涡旋MZM， 这有利于MZM电导行为的观测. STM技术具有亚Å的空间分辨率， 使用STM探针探测到的MZM电导信号更加局域， 具有更强的可信性. 在STM针尖反馈工作时， 针尖高度会随着隧穿电流(It)以及扫描偏压(Vs)的变化上下移动， 这个过程调节了隧道结大小(GN≡It/Vs)， 改变了针尖与样品的隧穿耦合强度( Gt，GN与 Gt正相关). 实验上可以通过这一技术连续增加隧穿耦合强度， 在 Gt远大于 kBT和 Gp时有希望观测到MZM的共振量子电导!

将STM探针定位于FeTe0.55Se0.45单晶涡旋MZM的正上方， 通过改变STM针尖高度的方法，实验上可以原位连续地测量MZM零偏压电导随隧穿耦合强度的变化(图11(a))[105]. 如图11(b)所示， STM实验在涡旋中心测量的dI/dV谱随隧道结的变化显示， MZM的零偏压电导在隧穿耦合足够强(GN≈ 0.3G0， G0= 2e2/h)时趋于饱和， 随着隧穿耦合进一步增加， MZM的零偏压电导出现平台行为. 与此同时， 超导能隙以外的电子连续态电导随着隧穿耦合的增加持续上升， 这一结果暗示针尖与涡旋MZM具有非平庸的隧穿耦合规律. 为了排除零偏压电导平台的可能平庸来源， 实验还测量了有限能量CdGM束缚态(图11(h))、零场超导能隙外连续态(图11(i))、零场零偏压(图11(j))电导随隧穿耦合强度的变化曲线， 研究表明这些实验条件下都不存在电导平台行为， 其中零场下的电导测量排除了量子弹道输运的可能性[219-224]. 本文5.1节介绍了CdGM束缚态波函数不满足电子-空穴等价性(图10(f))， 故而它与电子和空穴极的隧穿耦合强度不相等， 共振Andreev反射不能发生.一系列实验表明电导平台行为是涡旋MZM所特有的.

文献[105]对60个涡旋MZM进行了变隧道耦合强度的电导测量， 其中29个涡旋MZM在压低针尖的过程中变得不稳定， 涡旋蠕变逃逸导致实验失败. 而其余的31个涡旋MZM随着隧穿耦合超过某一阈值， MZM零偏压电导呈现平台行为.图11(g)总结了这31个涡旋MZM的电导平台值(Gp)， 实验发现大多数的涡旋MZM的零偏压电导平台为非量子化的任意值(0.2G0—1.0G0)， Gp分布的中心值约为0.6G0. 图11(c)和图11(d)中表示了一个典型的具有非量子化电导平台的涡旋MZM. 但是在总共的31次测量中， 实验发现了1个涡旋MZM其零偏压电导随着隧穿耦合强度增加持续上升， 在GN约为0.7G0时零偏压电导进入稳定的量子化平台(图11(e)和图11(f))， 这一行为与MIRAR的理论预期一致， 反映了MZM的Majorana本质性质.

非量子化的零偏压电导平台是FeTe0.55Se0.45单晶涡旋MZM的常见行为. 进一步实验发现[105]，对于具有非量子化电导平台特征的涡旋MZM， 人为增加STM能量展宽(增大lock-in激发电压)会降低涡旋MZM的平台电导值. 再者， 通过比较不同位置上的涡旋MZM行为， 实验发现增强基础准粒子中毒效应也会抑制其平台电导值. 本文在这里需要指出， 涡旋MZM的非量子化电导平台行为不能被5.1节中介绍的Majorana量子电导理论所解释， 虽然实验发现电导平台行为是MZM所特有的， 强烈地暗示MIRAR在这里发挥了重要作用，但是严格来讲， 并没有直接的实验证据表明非量子化的电导平台一定来自于非平庸的Majorana物理机理. 为了完全理解FeTe0.55Se0.45单晶涡旋MZM上观察到的非量子化电导平台特征， 还需要后续开展更多的理论和实验研究.

涡旋MZM零偏压电导平台(特别是量子化的电导平台(图11(e)和图11(f)))的发现， 首次从实验上提供了空间分辨的MIRAR证据， 这不仅是对MZM的Majorana本质(粒子-空穴等价性)的直接测量， 也为证明FeTe0.55Se0.45单晶涡旋中的ZBCP是MZM提供了进一步的支持证据.

6 测量涡旋MZM的拓扑本质: 全局束缚态半整数能级嬗移

MZM是拓扑非平庸的超导准粒子， MZM的出现总是伴随着非平庸的拓扑不变量[194-197]. 比如在本征拓扑超导体中(弱耦合的二维手性p波超导体[16]和一维p波超导Kitaev链[225])超导电性的非平庸拓扑性质可以通过由动量空间到准粒子旋量空间的映射体现， MZM是拓扑超导体边缘上激发的非平庸准粒子; 再比如在自赋性拓扑超导材料中， 涡旋MZM既可以看作是三维涡线模型中的一维拓扑超导体(涡线)对应的边界态， 也可以看作是二维Fu-Kane模型中拓扑非平庸的涡旋点缺陷上的束缚态(4.3节). 然而严格地讲， 存在MZM和存在拓扑超导电性两个命题之间互为非必要非充分条件[226]. MZM的出现既不要求超导电性一定是拓扑非平庸的， 也不要求正常态的能带一定是拓扑非平庸的， 但是MZM的出现一定伴随着明确的非平庸拓扑不变量. 对于有N个费米面的体系， 定义涡旋MZM拓扑不变量， 其中 wi是第i个费米面上的HBdG缠绕数， 需要同时考虑超导能隙和正常态能带的缠绕; mi是第i个费米面的超导所对应的涡旋数. 一般说来， 当 Z2=1 时存在涡旋MZM. 值得一提的是，Z2是演生拓扑不变量， 不依赖于超导体的体态拓扑结构， 拓扑平庸材料体系中也可以演生涡旋MZM[226，227，229]， 比如多分量超导体(例如自旋三重态超导、配对密度波超导、向列超导等)的分数磁通涡旋中可以存在涡旋MZM[227，230].

在Fu-Kane模型中， 涡旋MZM的出现可以通 过 Z2很 自 然 地 看 到( Z2=1×1 )， 这 里 涡 旋MZM的拓扑非平庸性主要得益于Dirac表面态自旋Berry相位的贡献( w =1 )[24]. 因此， 想要从实验上检验FeTe0.55Se0.45单晶涡旋MZM的拓扑本质， 需要测量Dirac表面态对涡旋束缚态产生的影响. 本文发现， 在超导涡旋准粒子激发的过程中，与常规s波超导体相比， Dirac表面态的参与赋予了涡旋束缚态额外的半整数角动量， 使得全局涡旋束缚态能级序列发生半整数能级嬗移， 这不仅产生了零能的MZM， 而且伴随着涡旋束缚态态密度空间图样序列的变化， 这些特征是对涡旋MZM拓扑本质的直接反映. 本节将详细讨论超导Dirac表面态演生涡旋束缚态的物理性质， 并介绍F eTe0.55Se0.45单晶全局涡旋束缚态的实验观测.

6.1 超导Dirac电子演生拓扑涡旋束缚态

首先， 本文介绍普通s波超导的磁通涡旋束缚态与束缚态量子极限的概念. 从第1节的介绍中知道普通s波超导的涡旋束缚态可以通过求解BdG方程获得[13，15]. 当参与演生涡旋束缚态的相关能带为抛物线能带时， 涡旋束缚态可以写成Eν≈ νΔ2/EF， 其中ν = n + 1/2 是涡旋束缚态的总角动量， 其取值为半整数(ν = ± 1/2， ± 3/2， ± 5/2，···). 当涡旋束缚态能级间距不太大时， 涡旋束缚态遵守半整数能级序列(图12(a))， 不存在零能束缚态， 这是常规s波超导体的普遍行为. 然而， 早期STM实验发现在常规s波超导体(如NbSe2)的涡旋中心存在巨大的ZBCP， ZBCP随着远离涡旋中心劈裂成两个对称的峰并呈现出空间色散分布(图12(b))[14，175，231]， 这一现象与BdG方程给出的半整数能级序列、空间分立解不符[13]. 另外， 当超导存在能隙节点时(比如d波超导体)， 超导磁通涡旋中将不再存在定义明确的“涡旋束缚态”， 超导准粒子与能隙外的连续态混合， 涡旋内超导准粒子的能量呈现空间连续色散分布[232-235]. 早期涡旋束缚态的STM观测反而与有能隙节点超导体的理论预期更吻合， 但这显然不符合实验事实， s波超导体不存在能隙节点.

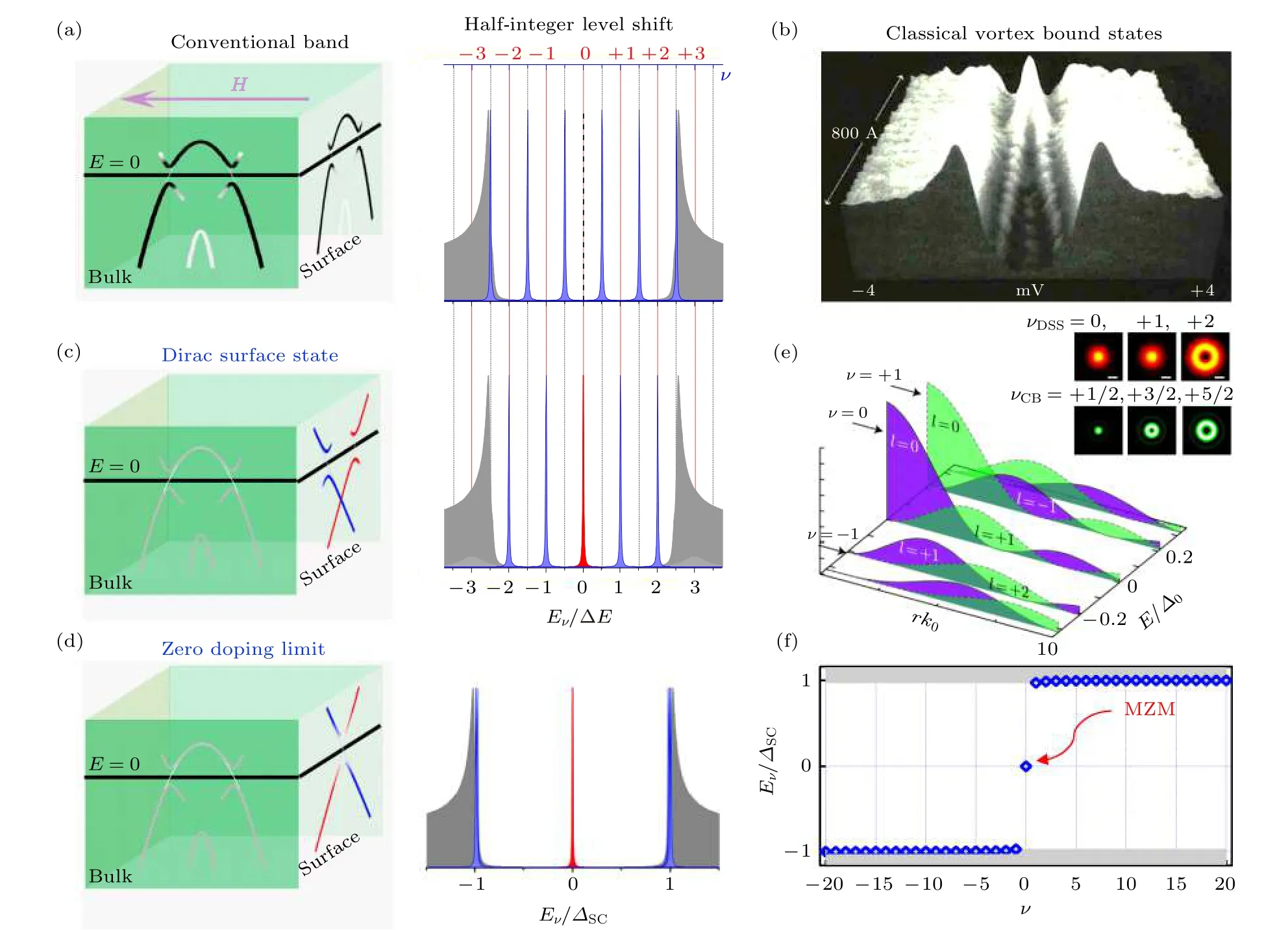
图 12 Dirac表面态导致涡旋束缚态半整数能级嬗移 (a)普通s波超导体的涡旋束缚态呈半整数能级序列分布， 其相关能带为常规的抛物线体能带[104]; (b)普通s波超导体的磁通涡旋未达到量子极限时(Texp ＜ TQL = TcΔ/EF)， 各级涡旋束缚态卷积在一起， 在空间上呈色散分布， 涡旋中心出现的巨大ZBCP， 为多个非零能束缚态的卷积[231]; (c) Fu-Kane模型的涡旋束缚态呈整数能级序列分布， 其相关能带为Dirac表面态， Dirac表面态引入了磁通涡旋束缚态的半整数能级嬗移[104]; (d)当Dirac表面态的化学势恰好位于Dirac点时称为零掺杂极限， 此时MZM是超导能隙内惟一允许的涡旋束缚态[104]; (e)磁通涡旋的相关能带为图(c)左图时， 涡旋束缚态的态密度径向空间分布， 紫色为准粒子自旋向下的组分， 绿色为准粒子自旋向上的组分[210]， 插图: Fu-Kane模型(红色)和普通s波超导体(绿色)磁通涡旋束缚态最低三能级的二维自旋积分态密度. Fu-Kane模型的磁通涡旋束缚态的最低两级波函数呈实心球分布， 而普通s波超导体中只有最低能级为实心球分布， 这一态密度空间图样的差别是涡旋束缚态半整数能级嬗移的强证据[104]; (f)理论计算的趋近零掺杂极限时的涡旋束缚态， 超导能隙中允许的束缚态只有MZM， 数值模拟中磁场方向选择为垂直样品表面向下(图(a)所示为实验中实际使用的磁场方向)Fig. 12. Surface Dirac electron induced half-integer level shift of vortex bound states: (a) Half-odd-integer quantized level sequences of vortex bound states in a conventional s-wave superconductor. There are only parabolic bulk bands involved[104]; (b) the quantum limit is difficult to reach in conventional s-wave superconductors， so that a large ZBCP observed in the center of vortex core is generally due to multiple overlapping of densely packed non-zero peaks[231]; (c) integer quantized level sequences of the vortex bound state in Fu-Kane model. The intrinsic spin Berry phase carried by Dirac surface states induces the half-integer level shift[104]; (d) the zero-doping limit is defined as the chemical potential is approaching the energy of the Dirac point. In this case， a vortex MZM is the only allowed subgap bound state[104]; (e) the theoretical calculated angular momentum resolved wavefunction of BdG eigenstate， the blue and green curves are spin down and up components， respectively[210]. Insert: The calculated spin-integrated 2 D local density of states of three lowest levels of vortex bound states in the case of (c) and (a)， respectively[104]; (f) theoretical calculated eigenvalue of BdG Hamiltonian near the zero chemical potential limit.

为了理解这一矛盾， 人们通过理论研究发现实验观测到的常规s波超导体涡旋束缚态的反常行为是由于实验温度未能达到涡旋束缚态的量子极限导致的[15]. 当温度展宽效应的影响小于涡旋束缚态的能级差时涡旋束缚态达到量子极限[236]， 这时才可以在实验中观测到量子化分立的束缚态. 当实验温度高于量子极限温度(TQL)时， 各涡旋束缚态能级重叠在一起表现为反常的连续色散行为. 量子极限温度可以按照如下方法估算: TQL= TcΔ/EF.常规s波超导体通常具有很大的费米能(EF≈2—10 eV)以及极小的超导能隙(Δ ≈ 1 meV)， 这导致涡旋束缚态能级差非常小， 量子极限温度极低， 实验上很难到达量子极限. 在这种情况下， 不同角动量的涡旋束缚态重叠在一起， 无法对束缚态能级序列行为进行仔细研究， 因此， 实现涡旋束缚态的量子极限是测量Dirac表面态对涡旋束缚态能级序列的影响的先决条件， 这需要材料具有高温超导和小费米能特征， 从第1节的讨论可知， 很多铁基超导体满足这些要求(图1(a))[237-242].

在介绍Dirac表面态演生涡旋束缚态的基本特征之前， 本节先介绍超导磁通涡旋的一般表达.超导磁通涡旋是第二类超导体在磁场下激发的拓扑缺陷， 超导能隙的幅值沿着径向趋近超导磁通涡旋中心时幅值逐渐减小并在涡旋中心变成零; 超导相位环绕涡旋中心变化， 在超导涡旋的边界(London穿透深度)上存在超导电流. 超导涡旋通常可以写成

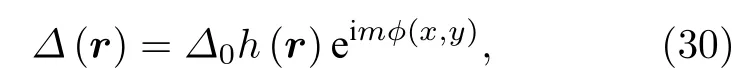
其中 Δ0是超导在正常区域的能隙幅值;h(r) 是以涡旋中心为原点的能隙幅值径向分布函数， 一般写成 h (r)=tanh(r/ξ) 或 者; m 是涡旋数， 取值为任意整数， 代表每绕涡旋一圈超导相位变化的圈数. φ (x，y) 是超导相位的空间分布， 对于最简单的情况， 单个磁通涡旋写为φ(x，y)=arctan(y/x) ; 涡旋-反涡旋对可以表示为φ(x，y)=arctan[2ay/(x2+ y2-a2)] ， 其中涡旋和反涡旋分别位于(a， 0)和(—a， 0)[243]. 涡旋和反涡旋按照涡旋缠绕数Zv的正负分别定义， Zv=， 其中c是绕涡旋中心的闭合环路[244].

超导Dirac表面态演生的涡旋束缚态可以通过求解实空间单个磁通涡旋的BdG方程获得[24，207，208]，

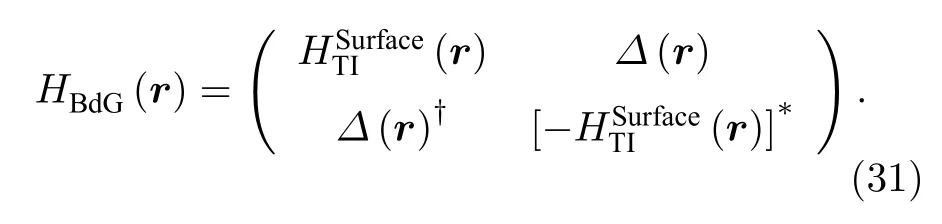
由于磁通涡旋具有旋转对称性， 涡旋束缚态的总角动量的垂直分量( Kz)是好的量子数， 即 [Kz，HBdG]=0 ， 因此涡旋束缚态的能量本征值可以用Kz的本征值(ν)来表示. 当Δ/EF不太大时， 涡旋束 缚态的能级序列可以近似写作:

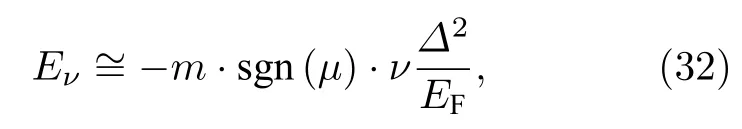
其中 m 是涡旋数; s gn(μ) 是Dirac表面态化学势的符号; ν 是总的垂直角动量. 可以证明， 在Dirac电子参与时，

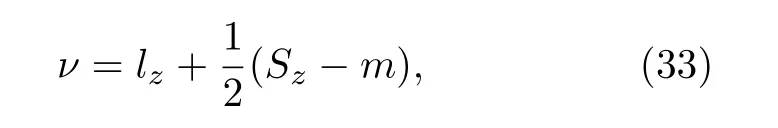
其中 lz是涡旋束缚态的轨道角动量， 取值为整数;Sz是自旋角动量， 对于自旋向上(向下)的成分取值为+1 (—1)[18，210，211]. 可见， 与常规s波超导体不同， 超导Dirac表面态演生的涡旋束缚态角动量 ν取值为任意整数(ν = 0， ± 1， ± 2， ± 3， ···)， 涡旋束缚态能级序列呈整数量子化分布， 其中ν = 0的束缚态就是涡旋MZM (图12(c)). 涡旋束缚态的这一特征是Dirac表面态额外引入的 Sz导致的[104]，对于常规s波超导体，

涡旋束缚态能级序列呈半整数量子化分布.Dirac表面态导致的涡旋束缚态能级序列的半整数嬗移是涡旋MZM拓扑本质的直接体现.

涡旋束缚态半整数能级嬗移也同时伴随着态密度空间图样序列的变化. 从4.1节的介绍可知，Fu-Kane模型导出的涡旋MZM的波函数正比于贝塞尔函数 Ji(x) . 本文在这里更清楚地指出，MZM波函数中贝塞尔函数的阶数由涡旋束缚态的轨道角动量决定， 即 i =lz. 由贝塞尔函数的性质可知，lz=0 分量的态密度最大值出现在磁通涡旋中心， 随着 lz增大态密度出现最大值的位置逐渐远离涡旋中心， 从态密度最大处向涡旋中心移动， 态密度逐渐减小. 结合涡旋束缚态能级序列的角动量分析， 不难得到束缚态各能级的角动量( ν，lz，Sz)以及各分量波函数的分布特征. 图12(e)理论计算了 m =-1 和μ ＞ 0时， 涡旋束缚态的态密度分布，其中紫色为自旋向下的成分， 绿色为自旋向上的成分[210]. 将同一能级所有成分的态密度求和即可得到各能级的总态密度特征， 这一信号可以利用STM恒能电导绘图直接观测. 可以发现， 在Dirac表面态参与的涡旋束缚态态密度空间图样序列中， 最低能的两个能级(ν = 0， +1 或—1)都为“实心分布” (图12(e)插图上排)， 与之相反， 在常规s波超导体的涡旋束缚态态密度空间图样序列中， 只有最低能级(ν = +1/2 或 —1/2)为“实心分布” (图12(e)插图下排)， 这是Dirac表面态诱导涡旋束缚态发生半整数能级嬗移的重要特征[104].此外， 使用(32)式—(34)式的波函数和能级角动量分析， 本文得到了Dirac表面态演生的涡旋束缚态的相关结论， 在这里不加推导罗列如下: 1)反转磁场方向改变涡旋数的符号， 同时改变 ν 与 Eν的正负关系， 但不改变第二实心分布能级的能量[106];2)改变化学势的符号会改变第二实心分布能级能量的符号， 也就是说，μ＞0 时第二实心分布能级出现在正能量，μ＜0 时第二实心分布能级出现在负能量; 3)涡旋中心的零能波函数的自旋总与磁场方向平行， 而涡旋中心第二实心分布能级波函数的自旋总与磁场方向反平行， 这一特征就是涡旋MZM的自旋分辨性质[62，208-211].

最后， 本节介绍超导Dirac表面态演生涡旋束缚态的零化学势极限行为. 我们在前面介绍的涡旋束缚态能级序列方程是只在小能级间隔条件下成立的近似方程. 而当Δ/EF很大时， 最低能非零涡旋束缚态能量将十分接近于超导能隙边， 由于量子限域效应的影响， 高阶涡旋束缚态只能位于超导能隙边和最低能非零涡旋束缚态能量之间， 这自然会打破涡旋束缚态能级序列的整数量子化分布. 实际上BdG方程的能量本征值在某些特定情况下具有严格解， 例如当选择时， 可以证明单量子化磁通涡旋 (|m|=1) 的束缚态能级存在严 格的解析表达式:

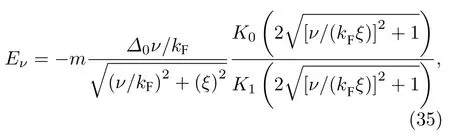
其中 Ki是McDonald函数[245]. 当化学势趋近于Dirac点时， 即 EF→0 ， MZM是超导能隙中惟一允许的涡旋束缚态(图12(d))[246，247]. 如图12(f)所示， 本文数值计算了 m = —1，μ→0+时的涡旋束缚态能级谱， 可见超导能隙中只有孤立的涡旋MZM， 其他非零能涡旋束缚态都被排斥到了超导能隙边缘， 这时涡旋MZM具有最大的拓扑能隙.

这里值得一提的是， 在 μ 严格为零时Fu-Kane模型演生出额外的赝手性对称性， 涡旋的拓扑分类相应发生变化(从Class-D变为Class-BDI， 拓扑不变量由Z2变为Z)[196]， 这使得涡旋MZM之间的两体杂化(Majorana hybridization)[248-250]被禁止， 导致通过编织MZM构建拓扑量子比特的方案失效. 但是赝手性对称性保护的简并涡旋MZM晶格具有绝对平坦的Majorana能带， 在这种平带体系中MZM四体相互作用(Majorana interaction)占据主导[251，252]， 这会演生出更多新奇的物理现象[253]， 如SYK模型、Majorana分数量子霍尔效应等. MZM相互作用超出了本文的讨论范围， 此处不再展开， 感兴趣的读者可以参考相关文献[253].

6.2 测量涡旋束缚态整数量子化能级序列

FeTe0.55Se0.45单晶具有很高的涡旋量子临界温度， 人们在早期实验中成功观测到了量子化涡旋束缚态[239]， 这为测量Dirac表面态演生的整数量子化能级序列， 检验涡旋MZM的拓扑本质提供了基础. 本文在第4节和第5节中只关心位于零能的涡旋MZM的性质， 因此实验中忽视了伴随MZM出现的其他涡旋束缚态的行为[102，105]. 随着对涡旋MZM拓扑本质的理解加深， 包含MZM的全局涡旋束缚态能级序列的特征被进一步深入研究， 本文下面将系统介绍相关实验进展.

在前面工作的基础上， 实验上利用极低温超高分辨率STM系统， 对FeTe0.55Se0.45单晶表面的磁通涡旋进行了更加深入的研究. 在把注意力转移到涡旋束缚态全局行为后(而不是仅关注零能模)， 实验研究很快发现在大多数含有涡旋MZM的磁通涡旋中涡旋MZM并非惟一的束缚态. 在极低温下， 不只是涡旋MZM， 其他有限能量束缚态也呈现量子化的空间分立分布， 这标志着FeTe0.55Se0.45单晶的涡旋束缚态达到了量子极限(图13(a)). 图13(b)将涡旋(#1)束缚态的能量/空间位置提取出来， 量子化束缚态的分立特征变得更加明显. 通过拟合可以发现各涡旋束缚态能级之间近似为等间距分布. 图13(c)将各级束缚态能量(EL)按照能级间隔(ΔE1)进行归一化， 可以发现涡旋束缚态遵循整数量子化的能级序列. 与此同时， 使用Fu-Kane模型可以以角动量为自变量数值计算涡旋#1涡旋束缚态的能量本征值. 理论计算的结果很好地重复了实验观测. 实验一共测量了35个具有整数量子化行为的磁通涡旋， 将这些磁通涡旋的归一化束缚态能量进行直方图统计分析(图13(i))， 可以看到明显的整数量子化特征.

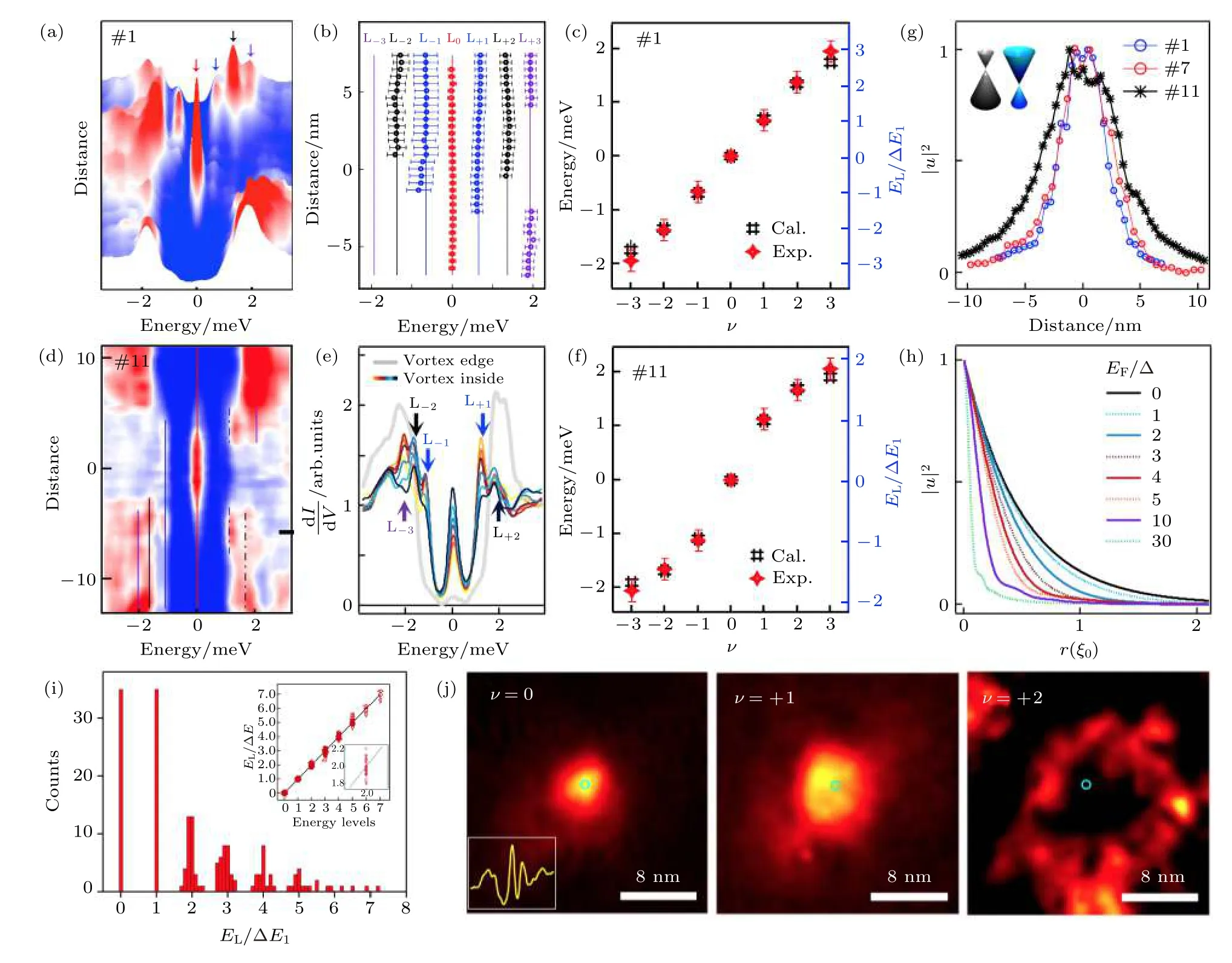
图 13 实验观测Dirac表面态导致的整数量子化涡旋束缚态[104] (a)拓扑涡旋#1的dI/dV(r， V)强度分布图， 整数量子化的涡旋束缚态能量呈分立分布， 且不随空间位置改变; (b)采用简单高斯拟合提取(a)中实验数据的束缚态峰位; (c)数值计算的#1磁通涡旋的束缚态能量与实验观测值的比较. 右侧坐标轴为使用束缚态能级间距归一化的束缚态能量， 能级序列具有明显的整数量子化特征; (d)拓扑涡旋#11的dI/dV(r， V)强度分布图， 这个涡旋靠近零掺杂极限; (e)图(d)的dI/dV谱， 在超导能隙附近具有量子化的高能涡旋涡旋束缚态; (f)与(c)相同， 是#11的情况; (g)整数量子化(红蓝圆圈)和近零掺杂极限下(黑星)的MZM强度空间分布; (h) Fu-Kane模型计算的不同化学势下的MZM波函数， 化学势越小MZM波函数空间分布越长; (i) 35个具有整数量子化行为的拓扑涡旋的直方图统计， 涡旋束缚态能量被能级间距归一化. 插图: 这35个涡旋所有涡旋束缚态归一化能量的分布图， 涡旋束缚态能量呈整数能级序列; (j)实验测量的整数量子化的拓扑涡旋最低能的三个涡旋束缚态的态密度空间分布， 与图12(e)中Dirac表面态演生涡旋束缚态的理论计算一致. 实验中磁场垂直样品表面向下Fig. 13. Observation of integer quantized vortex bound states[104]: (a) A dI/dV(r， V) line-cut intensity plot measured on a topological vortex #1. Integer quantized vortex bound states are clearly observed; (b) peak positions extracted from (a); (c) the comparison between experimental observed and theoretical calculated level energy in topological vortex #1; (d) same as (a)， but measured on vortex #11， which is close to the zero chemical potential limit; (e) overlapping display of dI/dV spectra selected from (d); (f) same as (c)， but shows the case of vortex #11; (g) the comparison of observed MZM line profile in topological vortices under integer quantization (open circles) and near the zero chemical potential limit (dark stars); (h) the calculated MZM wavefuction under different chemical potential by Fu-Kane model; (i) a histogram of averaged level energies normalized by the first level spacing， i.e. the ratio EL/ΔE. The statistical analysis is performed among all the 35 topological vortices which show integer quantized CdGMs levels; (j) experimentally observed spatial pattern of the lowest three levels of vortex bound state in a topological vortex.

本文在6.1节中已经介绍， 涡旋束缚态的整数量子化能级序列得益于Dirac表面态额外提供的半整数自旋角动量. 在产生整数量子化能级序列的同时， 也使态密度空间分布序列出现双“实心”能级， 考虑到FeTe0.55Se0.45单晶的Dirac表面态具有正化学势， 第二实心能级应该出现在正偏压一侧[207]. 为了确保图13(a)—图13(c)中测量到的整数化能级序列的确来自于Dirac表面态的贡献(而不是其他因素造成的巧合)， 实验测量了整数量子化磁通涡旋的第0， +1和+2级涡旋束缚态能量位置的恒能电导绘图(图13(j))， 这是对选定能量局域态密度的直接测量. 实验结果与理论预期一致(图12(e)). 值得指出的是， ν = +2级圆环图样的清晰观测得益于FeTe0.55Se0.45单晶Dirac表面态具有很小的kF(约 0.02 Å—1) (图3). 仔细研究图12(e)中的理论计算可以发现， 涡旋束缚态的高轨道角动量波函数出现最大值的空间位置正比于Dirac表面态费米波矢的倒数(正比于1/kF)，Dirac表面态的kF越小， 束缚态态密度的空间震荡周期越大， 越便于使用STM恒能电导绘图的方法进行观测. 而FeTe0.55Se0.45单晶的体态kF大约为0.1 Å—1， 涡旋束缚态态密度的空间震荡周期过小，很容易被材料本身的电子不均性掩盖， 不利于空间图样的观测. 这些结果表明， 对FeTe0.55Se0.45单晶涡旋束缚态的系统性实验研究成功观测到了超导Dirac表面态演生的整数量子化涡旋束缚态.

在FeTe0.55Se0.45单晶上的部分磁通涡旋中，超导能隙以内只有醒目的MZM， 而其他涡旋束缚态明显打破了整数量子化能级序列， 实验发现在超导能隙沿上有难以辨认的态密度峰， 这其实来源于高能涡旋束缚态. 这种行为是近零化学势极限的表现. 在掺杂拓扑绝缘体等体系中， 实验确切地发现化学势存在空间不均匀性[254-257]， FeTe0.55Se0.45单晶具有阴离子位掺杂， 我们可以相信这里同样存在化学势的空间起伏， 这使得材料表面的某些位置十分接近零掺杂极限， 造成了涡旋MZM在STS谱上的孤立行为. 图13(d)—图13(f)是对图7中测量到的涡旋束缚态数据的再分析， 本文在第4节中只关注零能模的行为而忽视超导能隙内的其他特征，然而在这里通过仔细分析可以发现在超导能隙边沿上存在3个量子化分立的涡旋束缚态， 他们的归一化能级分布如图13(f)所示， 显然， 这种情况下的涡旋束缚态不符合整数量子化特征. 使用图13(c)中的理论模型并减小模拟所用的化学势的值， 数值计算的结果很好地重复了实验观测， 这支持近零化学势极限的解释. 为了使结论更可信， 实验还分析了整数量子化和MZM孤立行为的磁通涡旋中MZM强度的空间分布曲线(图13(g))， 实验发现与整数量子化行为的涡旋MZM相比， 图13(d)的涡旋MZM具有更宽的空间分布. 结合第4节介绍的涡旋MZM波函数表达式， 理论计算了不同EF条件下的|u|2， 理论结果表明减小EF可以增加涡旋MZM波函数的空间分布(图13(h))[24，210]， 这进一步支持图13(d)中的涡旋处于近零化学势极限的结论.

伴随涡旋MZM出现的整数量子化和近零化学势极限行为的涡旋束缚态都是Dirac表面态导致的整数角动量量子数的体现.

6.3 样品不均性带来的意外收获: 共存平庸涡旋中的半整数能级序列

伴随涡旋MZM出现的整数量子化能级序列的成功观测证明了Dirac表面态额外引入的半整数自旋角动量导致涡旋发生半整数能级嬗移， 演生出零级束缚态—涡旋MZM. 尽管材料中应该存在两种不同的涡旋束缚态能级序列(整数量子化的拓扑涡旋和半整数量子化平庸涡旋)， 然而通常情况下单一材料具有统一的拓扑性质， 这一限制使得同一块样品中的涡旋束缚态只能呈现一种能级分布， 妨碍了两种束缚态的直接比较， 以及半整数能级嬗移的直接观测. 由于阴离子位掺杂的缘故，FeTe0.55Se0.45单晶具有本质不均性[258-261]， 这一现实因素一定程度上降低了表面涡旋中出现MZM的概率， 一直以来被视为演生涡旋MZM的不利因素(第4节)， 但是FeTe0.55Se0.45单晶的本征不均性在这里反而成为了一道曙光， 不均性使得样品性质更加丰富， 两种涡旋可以在同一块样品的同一片区域出现. 这使得在相同的实验参数下直接对比拓扑涡旋和平庸涡旋成为了可能， 也为直接鉴定表现涡旋MZM拓扑本质的半整数能级嬗移提供了稀有机会.

FeTe0.55Se0.45类似合金， 具有多维度的本征不均性， 实验研究发现它的表面存在化学组分、化学势、无序和散射势以及超导能隙的空间不均匀. 本文在前面已经介绍了超导能隙和化学势的空间涨落导致部分拓扑涡旋表现出近零化学势极限特征(6.2节)， 较大的化学势涨落还有可能引发涡线拓扑相变(4.3节)， 而基础准粒子中毒效应的空间不均性可能来源于无序和散射强度的不均匀(4.2节). 在上述现象中， 材料的不均性直接影响了低能超导准粒子的行为， 因此本文暂且将导致这些现象的不均性命名为“弱不均”. 与此相反，FeTe0.55Se0.45单晶中的“强不均”效应可以直接杀死强拓扑绝缘体态， 使得样品(001)外表面的某些区域上不存在Dirac表面态， 在这里， 材料内部出现新的拓扑/非拓扑边界， 原本出现在材料外表面的Dirac表面态进入材料内部(图16(a))分布在新边界上， 而在这一区域的外表面上出现的平庸涡旋遵循半整数量子化特征. 在低温和低磁场条件下，实验观测到FeTe0.55Se0.45单晶表面的拓扑涡旋和平庸涡旋总是成群出现， 这支持Dirac表面态在表面某些区域消失(图15)的推论. 本文下面介绍两种可能的“强不均”机制， 它们破坏了表面附近部分体材料的强拓扑绝缘体态.

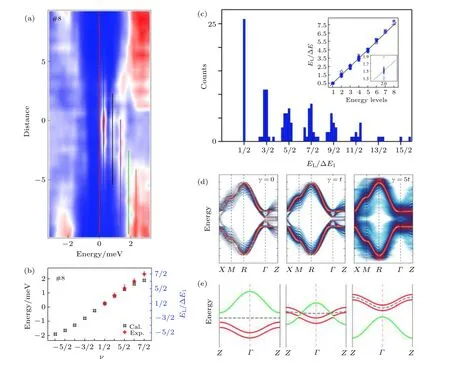
图 14 材料不均性帮助平庸涡旋共存 (a)平庸涡旋#8的dI/dV(r， V)强度分布图， 半整数量子化的涡旋束缚态能量呈分立分布， 且不随空间位置改变[104]; (b)数值计算的#8磁通涡旋的束缚态能量与实验观测值的比较， 右侧坐标轴为使用束缚态能级间距归一化的束缚态能量， 能级序列具有明显的半整数量子化特征[104]; (c) 26个具有半整数量子化行为的平庸涡旋的直方图统计，涡旋束缚态能量被能级间距归一化， 插图: 26个涡旋所有涡旋束缚态归一化能量的分布图， 涡旋束缚态能量呈半整数能级序列[104];(d)无序可以将强拓扑绝缘体变为普通绝缘体， 从左到右非磁性散射势逐渐增强[262]; (e)掺杂可以将强拓扑绝缘体变为弱拓扑绝缘体， 从左到右Te含量依此变大， 三个状态分别为普通绝缘体、强拓扑绝缘体、弱拓扑绝缘体. 绿色能带为奇宇称的pz轨道， 红色能带为偶宇称的dyz和dxz[201]Fig. 14. The inhomogeneity of material helps coexisting ordinary and topological vortices: (a) A dI/dV(r， V) line-cut intensity plot measured on ordinary vortex #8. Half-odd-integer quantized vortex bound states are clearly observed[104]; (b) the comparison between experimental observed and theoretical calculated level energy in ordinary vortex #8[104]; (c) a histogram of averaged level energies normalized by the first level spacing， i.e. the ratio EL/ΔE. The statistical analysis is performed among all the 26 ordinary vortices which show half-odd-integer quantized CdGM levels[104]; (d) surface disorder transforms the strong topological insulator to a normal insulator. The scattering potentials are gradually larger from left to right[262]; (e) concentration of the dopants could drive a strong topological insulator to be a normal insulator or weak topological insulator in Fe(Te， Se). The bands in green (red) represent pz (dxz/dyz) orbital with odd (even) parity[201].

1)强无序带来的非磁性散射会将强拓扑绝缘体态变为普通绝缘体态. 通常来说， 强拓扑绝缘体态受时间反演对称性保护， 非磁性杂质不能破坏Dirac拓扑表面态[25]. 但是这种拓扑保护只在弱杂质散射条件下成立， 当杂质或无序引入的非磁性散射势与体能带的拓扑能隙相近时， 强拓扑绝缘体态被破坏， 理论计算也证实了Dirac表面态在强散射势条件下消失(图14(d)). 在2.2节中， 本文通过超高分辨ARPES测量推算出FeTe0.55Se0.45单晶的体态能带的SOC能隙约为20 meV (图4(f))， 这远远小于经典拓扑绝缘体Bi2Se3的拓扑能隙(约300 meV). 因此， 虽然受拓扑性质保护的Dirac表面态应该是鲁棒且普遍的， 但是FeTe0.55Se0.45单晶能带的小拓扑能隙使得拓扑性质本身并不鲁棒，在材料“强不均”作用下， 某些区域变成普通绝缘体， 导致了平庸涡旋的出现[262-264].

2)阴离子化学成分的强起伏会将强拓扑绝缘体态变为普通绝缘体或弱拓扑绝缘体态[265，266](图14(e)). 本文2.1节中介绍了Fe(Te， Se)单晶的拓扑能带理论， 在富Se的样品中不存在拓扑能带， 随着Te原子的掺杂， Z点发生能带反转， 材料进入强拓扑绝缘体态. 然而我们注意到， 如果继续进行Te原子掺杂， 奇宇称的pz能带在G点也会发生反转， 这时材料进入弱拓扑绝缘体态， 自旋轨道锁定的拓扑表面态只存在于侧表面[265，266]. 因此，无论是过度富Se还是过度富Te都会使(001)表面上的Dirac表面态消失， 从而导致半整数量子化的平庸涡旋在某些区域出现[201，267，268].

在上述理论的启发下， 极低温超高分辨STM实验在FeTe0.55Se0.45单晶表面测量到了共存的平庸涡旋(图14(a)—图14(c)). 在对测量到的26个平庸涡旋使用6.2节中相同的分析方法之后，实验发现它们的涡旋束缚态呈很好的半整数量子化能级序列， 同样， 数值模拟可以重现实验观测.得益于FeTe0.55Se0.45单晶的“强不均”效应， 这些不含有零能模的半整数量子化平庸涡旋出现在(001)表面没有Dirac电子的区域上， 并在同一块样品中与含有涡旋MZM的整数量子化拓扑涡旋共存. 这样在相同实验条件下实现了具有不同拓扑性质的Dirac表面态和常规能带所演生的两种涡旋束缚态的直接对比， 鉴定出了超导Dirac电子诱发的半整数能级嬗移(图12(a)和图12(c))， 这是涡旋MZM拓扑本质的直接体现.

这项工作开创性地将涡旋MZM的拓扑本质与涡旋束缚态的全局行为建立联系， 不仅研究了涡旋MZM的拓扑性质， 而且进一步证明了铁基超导体超导涡旋中观测到的鲁棒ZBCP是MZM.

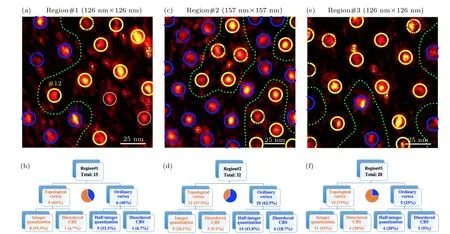
图 15 两种涡旋的空间分布[104] (a)， (c)， (e)在极低温(40 mK)和弱磁场(2 T)条件下测量的零偏压电导绘图. 随机挑选的三个区域相隔很远. 对这三个区域出现的磁通涡旋进行无差别dI/dV(r， V)测量， 用来鉴别各涡旋的束缚态行为. 其中黄色圆圈标记的涡旋代表存在涡旋MZM的拓扑涡旋， 蓝色圆圈标记的为不存在涡旋MZM的平庸涡旋， 实(虚)线圆圈代表(不)符合整数/半整数量子化行为， 绿色点线将同类涡旋围在一起， 可见同类涡旋总是成群出现， 这表明不均性导致样品表面某些区域Dirac表面态消失， 而在其他区域Dirac表面态保持完好; (b)， (d)， (f)三个区域中不同类型涡旋的统计数据， 数据测量条件为40 mK， 2.0 TFig. 15. Spatial distribution of the two classes of vortices[104]: (a)， (c)， (e) Zero-bias conductance maps of three well-separated regions. The yellow solid circles mark the vortices with ZBCPs and integer quantized CdGM levels， yellow dashed circles mark the vortices with ZBCPs but its CdGM level sequences can not be fitted to integer quantization， blue solid circles mark the vortices without ZBCPs and half-integer quantized CdGM levels， and blue dashed circles mark the vortices without ZBCPs or half-integer quantized CBS levels. The green dashed lines encircle the same class of vortices. Topological vortices and ordinary vortices usually group together， which indicates topological region and trivial region coexist on the sample surface due to spatial inhomogeneity; (b)，(d)， (f) summary of the ratio of different types of vortices in the three regions， respectively. The data in the three regions are measured under 40 mK and 2.0 T.

7 从量子物理到量子工程: 超导涡旋中MZM存在与否的机理讨论

本文在上节详细介绍了FeTe0.55Se0.45单晶样品表面两种涡旋的共存， 这同时也间接指出在实验观测中不是所有磁通涡旋都存在涡旋 MZM这一问题， 真实样品的三维特性(第4节)以及本征不均性导致了复杂的涡旋形态和分布特征. 从研究涡旋MZM物理性质的角度考虑， 真实样品的不完美是大自然的馈赠， 这使得在同一块样品中直接比较束缚态的两种拓扑成为可能. 但这就像是一枚硬币的正反面， 从发展拓扑量子计算的角度考虑， 真实样品的不完美却是一场噩梦. 本文前面的6节结合简洁的理论模型详细介绍了铁基超导体涡旋MZM的基本性质和实验观测， 这些只考虑完美情况的简单模型却往往最深刻地抓住了奇异现象的物理本质(第4节)——这是物理学研究的思路. 然而真实材料不是简单的物理模型， 材料或环境的不完美引入了其他影响因素， 这干扰了目标物理现象的实现， 但却是发展工程应用(例如拓扑量子计算)必须解决的问题——这是量子工程的任务. 因此， 为了在铁基超导体上实现拓扑量子计算这一终极目标， 实验研究涡旋MZM在材料表面的宏观分布特征， 并理论探讨影响涡旋MZM出现或不出现的物理机理具有深远的意义.

在讨论机理之前， 本节先介绍实验观测到的FeTe0.55Se0.45单晶表面涡旋MZM的宏观分布特征[104]. 早期实验在较高温度(约450 mK)下进行，这一条件下只有不到20%的磁通涡旋中存在涡旋MZM， 很难进行有效统计[102]. 得益于对额外准粒子中毒效应(4.2节)的深入研究， 本研究团队意识到更低温的实验条件有利于获得涡旋MZM的真实分布情况. 如图15所示， 在低温(40 mK)和低场(2 T)实验条件下随机选择了三个相距很远的区域， 无差别地测量了出现的76个磁通涡旋的束缚态空间分布信息. 通过利用图13和图14相同的数据分析方法， 实验鉴别出了每一个磁通涡旋的种类， 其中黄色圆圈标记的是有涡旋MZM的拓扑涡旋， 蓝色圆圈标记的是不存在涡旋MZM的平庸涡旋， 圆圈为实(虚)线的代表涡旋束缚态(不)遵循整数或半整数量子化能级序列. 这三个区域中涡旋种类的统计情况列在图15(b)， 图15(d)和图15(f)中. 从这些数据中可以得到三个结论:1)涡旋MZM的出现率在空间中具有很大的波动. 数据显示， 各区域涡旋MZM的出现概率为37%—75%不等. 由于这三个区域都是随机挑选的， 这表明FeTe0.55Se0.45单晶大尺度不均性对涡旋MZM的出现概率具有重要影响， 这暗示单晶质量的重要性; 2)实验发现76%的磁通涡旋束缚态遵循整数或半整数量子化能级序列; 3)同种涡旋往往成群出现， 图15中用绿色点线将同种涡旋圈在一起， 这一现象支持材料表面某些区域Dirac表面态消失而在其他区域Dirac表面态仍然保持完好的设想.

本文在前面零散地涉及了材料的三维特性和不完美性对涡旋中是否存在MZM的影响， 同时也指出理想情况下涡旋MZM的行为可以由Fu-Kane模型很好地描述. 为了回答真实材料和实际实验中并非每个涡旋中都存在MZM的问题， 本节下面将系统整理总结影响涡旋MZM是否出现的可能微观机制[104].

首先， 材料的“强不均”机制使得样品(001)表面的某些区域上Dirac表面态消失， 材料表面拓扑区域(有Dirac表面态)和常规区域(无Dirac表面态)共存， 在这两个区域上分别出现有涡旋MZM的拓扑涡旋和无涡旋MZM的平庸涡旋.

其次， 在确定的空间位置上以下因素会影响涡旋MZM的存否.

1）涡线拓扑相变会改变MZM的拓扑不变量[176]. 本文在 4.3节中仔细讨论了涡线拓扑相变的影响， 对于拓扑区域上的涡旋来讲， 发生涡线拓扑相变会导致涡旋MZM消失， 对于常规区域上的涡旋来讲相变导致MZM产生.

2）准粒子中毒效应会抑制涡旋MZM. 此项有三个方面: 第一， 当体态能带参与涡旋束缚态激发时， 一维涡线体内的微小能隙(δ)保护了末端的涡旋MZM， MZM沿垂直方向的波函数局域长度正比与1/δ， 当改变涡线的量子参数， 趋近于量子相变点时， MZM波函数将深入材料体内从而变得实验不可见. 继续改变量子参数直到达到相变点时，一维涡线的能隙关闭， 上下表面的两个MZM杂化消失; 第二， 高温下存在额外准粒子中毒效应(4.2节). 这导致了涡旋MZM在高温下消失; 第三， 基础准粒子中毒效应的空间不均性改变了MZM的有效温度， 这导致在同一实验温度条件下测量到的涡旋MZM具有不同的强度.

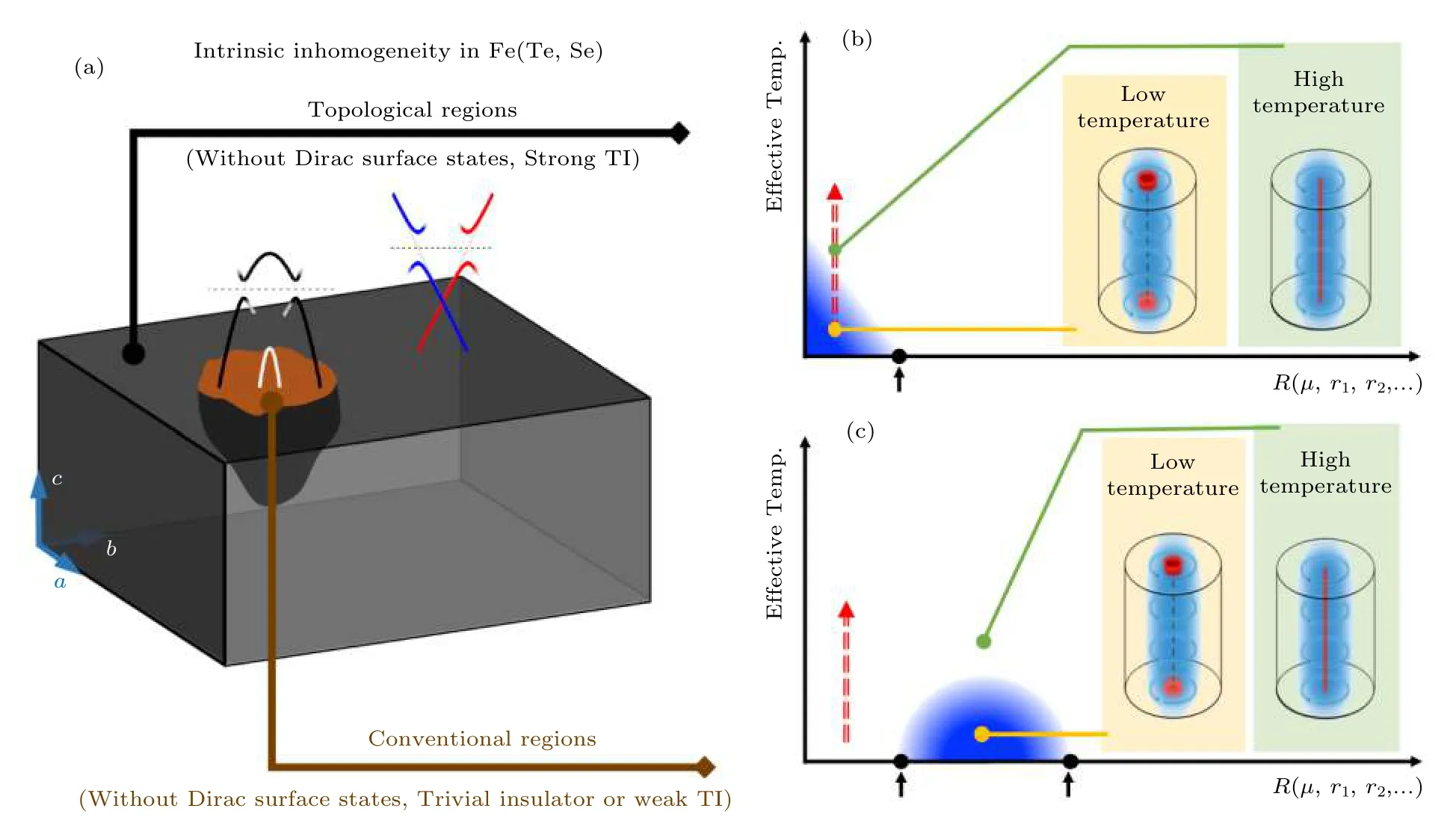
图 16 Fe(Te， Se)涡旋中有无MZM的微观机制[104] (a)材料不均性导致的两种表面共存， 其中棕色表面无Dirac表面态， 对应的体态为普通绝缘体或弱拓扑态; (b)在有Dirac表面态的表面区域上涡旋MZM的经验相图; (c)在没有Dirac表面态的表面区域上涡旋MZM的经验相图， 其中相图中蓝色越深的区域代表涡旋MZM越强， 更易被STM实验观测; 颜色越淡代表涡旋MZM强度越弱， 不易被观测; 横轴代表驱动涡线量子相变的量子参数， 比如化学势、Zeeman能等; 纵轴是MZM的有效温度， 包括温度展宽、仪器展宽、基础准粒子中毒展宽等; 红色点线表示估计的目前实验可以覆盖的相区Fig. 16. Mechanism of the presence or absence of MZMs in Fe(Te， Se)[104]: (a) Fe(Te， Se) single crystals are intrinsically inhomogeneous.Disappearance of Dirac surface states is possible in some regions of the (001) surface (brown color). In the conventional regions， the corresponding bulk states can be normal insulators or weak topological insulators. Consequently， the Dirac surface state moves deeper into the bulk and go around the conventional region， as indicated by the gray boundary inside the crystal. In other topological regions (gray color)， where Dirac surface states remain intact， the corresponding bulk states are still in the strong topological insulating phase; (b) a schematic phase diagram of vortex MZMs appearing in topological regions (topological vortices). The gradient blue areas in (b) and (c) indicate the phase sector that MZMs can be detected by STM/S experiments. In the dark blue sector，the Majorana wave function is more localized on the sample surface， while in brighter positions， the Majorana wave function strongly hybridizes with bulk quasiparticles and moves deeper beneath the surface， leading to weak ZBCP signal measured by STM/S. The vertical axis demonstrates MZMs evolution as a function of effective temperature which can be represented by extrinsic broadening of the observed ZBCPs. The horizontal axis demonstrates the MZMs evolution as a function of quantum parameters，e.g.， chemical potential (μ) measured from the Dirac point. The black dots with an arrow indicate the quantum critical points in which a vortex phase transition happens. Across the critical point， the vortex line turns to be topological trivial and MZMs disappear in the topological region. The red dashed line indicates the achievable region in experiments; (c) a schematic phase diagram of vortex MZMs appearing in conventional regions (ordinary vortices). There are no MZMs in our measurements in those vortices. The observable MZMs can only exist above the critical points when the vortex phase transition turns the trivial vortex line into a 1D topological superconductor in the conventional region.

如图16所示， 本文将上述因素总结成弱磁场下的涡旋MZM的经验相图， 其中红色点线是估计的目前实验可以涵盖的相区.

最后我们特别指出， 涡旋间距随着磁场升高而减小， 在强磁场下涡旋MZM面内杂化将成为控制涡旋MZM有无的主要因素. 多个STM实验观测到涡旋MZM的出现概率随磁场增加而减少[269，270]，随后不久， 这一现象被无序晶格涡旋MZM波函数杂化理论所解释[271].

8 总结与展望

从起源到发展， 从理论到实验， 从能带到准粒子， 从物理大局到工程细节， 本文循着一以贯之的逻辑线， 系统全面地介绍了Fe(Te， Se)单晶中演生涡旋MZM的研究进展， 旨在搭建经典Majorana理论和新兴铁基超导实验之间的桥梁，帮助读者对铁基超导材料中演生的涡旋MZM产生深刻理解和合理评价.

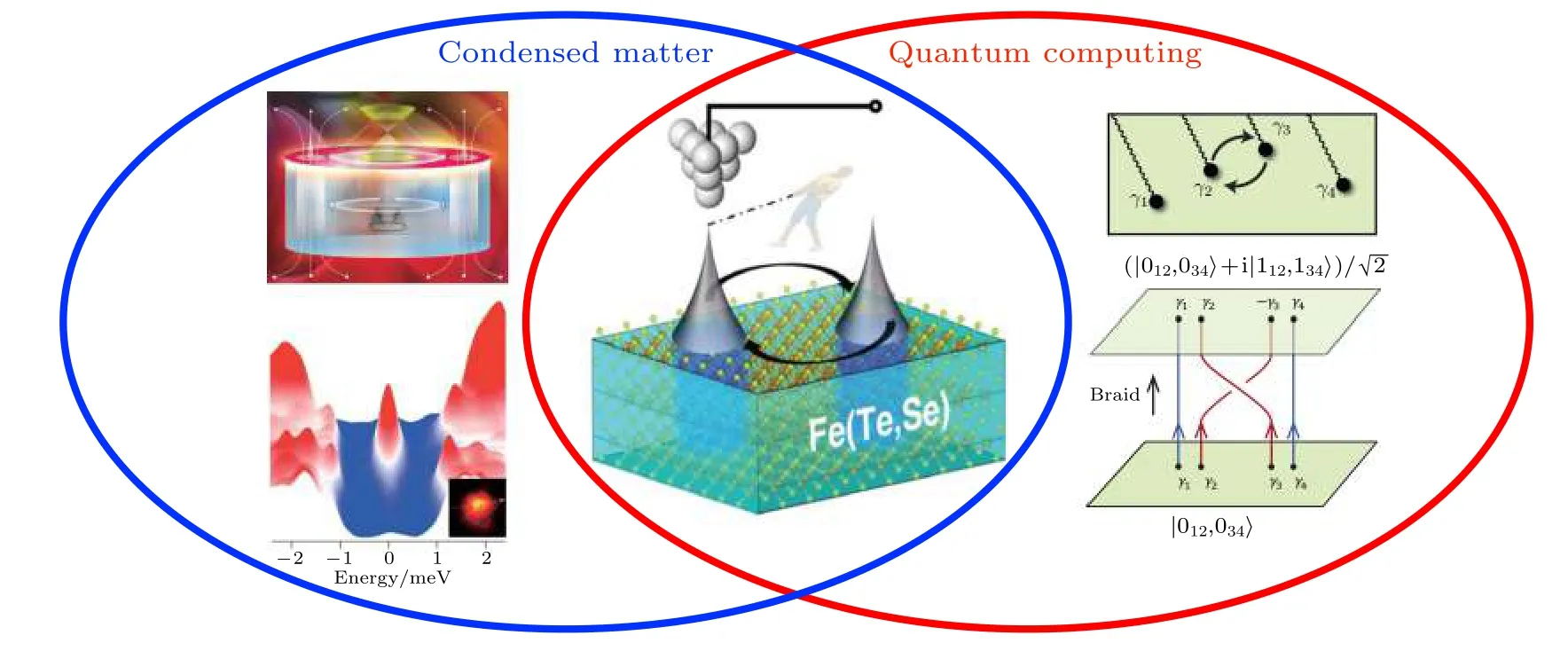
图 17 编织涡旋MZM， 探索拓扑量子计算. 左上: 拓扑铁基超导体中体超导k-近邻效应诱导的表面等效无自旋手性p波配对[84];左下: Fe(Te， Se)单晶中纯净的涡旋MZM[103]; 中间: 利用STM针尖操纵铁基超导表面的涡旋MZM[102]; 右图: 涡旋MZM编织操作与拓扑量子比特[3] (本图部分为原创)Fig. 17. Braiding vortex MZMs and topological quantum computing. Left-top panel: Surface effective spinless p-wave pairing induce by k-proximity effect from bulk bands in Fe(Te， Se)[84]. Left-bottom panel: The pristine vortex MZM observed in Fe(Te，Se)[103]. Middle panel: It is possible to use a STM tip to manipulate vortex MZMs on the surface of Fe(Te， Se)[102]. Right panel: Topological qubit built by braiding four vortex MZMs[3].

自从Fe(Te， Se)单晶作为新兴的Majorana准粒子载体被大家所认识， 铁基超导家族的拓扑性质迅速激起了学界的广泛关注. 在过去的几年里，大量新奇的理论和实验相继出现， 本文在这里尝试将其总结如下: 1)涡旋MZM的独立验证[269-272]，Fe(Te， Se)单晶中的涡旋MZM已经被多个研究团队独立验证; 2)铁基体系涡线拓扑相变理论的发展[200-203]; 3)发现铁基超导体拓扑性质的普遍性. 人们不仅发现铁基超导体拓扑非平庸的能带结构具有普遍性[101]， 还在铁基超导家族的多个其他材料中先后证实了涡旋MZM的存在， 比如(Li， Fe)OHFeSe[273，274]， CaKFe4As4[106]等; 4)探索潜在的更高温材料. 实验证明单层铁基超导Fe(Te， Se)薄膜具有非平庸的拓扑能带[267，268]， 单层Fe(Te， Se)薄膜同时还具有很高的超导转变温度， 这暗示单层铁基超导材料有可能成为液氦温度以上的高温Majorana载体[71]; 5)缺陷态理论和实验蓬勃发展.人们在铁基超导体磁性点杂质[99，275-278]、台阶边[279]、畴界[272]及原子线缺位[280-282]上观察到了Majorana模式的迹象， 这有待进一步验证; 6)表面态潜在的竞争超导序[283-285]; 7)潜在的表面和体态本征拓扑超导[286，287]; 8) 以Fe(Te， Se)为超导衬底的异质结表面的奇异行为[288-292]; 9)尝试优化样品质量[293];10)对表面态超导考虑完整的体态超导配对(s±)时， 在样品边界上获得保持时间反演对称性的Majorana模[294，295]; 11)巧妙设计结构， 实现单个的高阶MZM[296-299]; 12)探索可行的编织方案[300-302];13)铁基Majorana载体的发展也在一定程度上启发并促进了物理学家们在其他自赋性拓扑超导材料中研究Majorana准粒子[303-305]. 这一领域的蓬勃发展不仅为Majorana物理打开了新天地， 也为高温超导研究注入了一剂强心剂.

拓扑铁基超导体是当下最为可信的Majorana载体之一. 在现有工作的基础上继续深入研究涡旋MZM的性质， 尝试实现涡旋MZM的杂化、编织、融合以及费米宇称读取， 是拓扑铁基超导体系未来工作的重要方向. 这些目标的实现需要理论、材料和技术等多个方面的共同努力. 理论方面， 需要考虑涡旋MZM的真实情景， 设计出切实可行的编织方案[306]; 材料方面， 需要进一步提升样品质量，把材料的体和表面都做得更均一， 同时更要兼顾准粒子的拓扑能隙(能带工程视角)， 实现液氦温区的涡旋MZM; 技术方面， 需要探索可控的涡旋操纵手段， 实现操纵效率与准粒子寿命的匹配. 在此前提下， 我们将有机会构造拓扑量子比特， 让凝聚态物理和量子计算在拓扑铁基超导体上交融(图17).

本文介绍的系统性工作标志着拓扑铁基超导体系迈出了探索拓扑量子计算的“万里长征第一步”. 行远者必自迩， 经之营之， 未来可期.