特征γ射线谱分析的蒙特卡罗模拟技术*

邓力 李瑞 王鑫 付元光

1) (北京应用物理与计算数学研究所， 北京 100094)2) (中物院高性能数值模拟软件中心， 北京 100088)(2020 年2 月24日收到; 2020 年3 月23日收到修改稿)

蒙特卡罗方法(MC)是模拟核探测问题的理想方法， 用中子照射客体， 中子诱发产生非弹γ和俘获γ， 通过特征γ射线能谱和时间谱分析， 确定客体核素组成和重量百分比. 本文基于非弹γ和俘获γ时间门测量技术， 给出了脉冲源发射下探测器响应计数公式. 在中子与核作用产生次级光子方面， 采用期望值估计(expect value estimator， EVE)产光. 为了避免大量小权光子模拟带来的计算存储量增加， 设计了EVE产光与直接估计(direct estimator， DE)产光耦合. 仅增加少量计算时间， 便实现了特征γ射线解谱. 数值模拟在自主MC软件JMCT上开展， 计算结果初步验证了方法的正确有效性.

1 引 言

蒙特卡罗方法(Monte Carlo， MC)具有模拟核探测问题的天然优势， 近年已广泛用于X-射线荧光分析， 在线中子俘获瞬发γ射线分析，基于γ射线光谱的脉冲中子孔隙度测井， 隐藏爆炸物探测等. 相比X光常规探测， 中子诱发γ射线探测具有穿透能力强， 容易穿透包括钢、常规/化学武器包壳、核武器内部结构， 可用于确定客体的化学变化等， 这是核探测的优势所在.

目前核探测的主要手段是利用高能中子照射客体， 产生次级光子， 通过特征γ射线能谱、时间谱测量， 确定客体核素组成及份额. 在中子作用下，绝大部分元素都可以发射可辨认的特征γ谱线， 慢中子可以引起除氮以外所有元素的非弹性散射反应， 并发射特征γ谱线. 利用特征γ射线原级线光子不随入射中子能量变化这一特点， 通过特征γ射线的能峰特征， 确定客体内所含核素， 通过特征γ射线直穿贡献， 确定客体核素份额. 方法可用于化学/常规武器甄别、隐藏爆炸物/毒品探测、放射性石油测井和探测器灵敏度优化设计等.

由于核探测环境复杂， 涉及空间r、能量E、方向Ω、时间t七维变量的Boltzmann方程求解， 一般采用连续能量MC求解. 目前包括著名的MCNP[1]程序， 特征γ射线解谱还存在一定困难，虽然F8计数理论上能够算出探测器响应-脉冲高度谱， 但代价大， 解很难收敛. 另外， 中子产生次级光子采用直接估计， 存在随机因素的影响， 无法保证不漏掉某些重要核素的贡献. 文献[2-6]在这方面开展了大量研究， 针对特征γ射线解谱， 发展了多项技巧. 我们参考了其部分研究成果， 近期在自主MC粒子输运软件JMCT[7-12]上开发了特征γ射线分类标识计算及非弹γ射线和俘获γ射线时间箱计数方法. 特别在中子与核作用产生次级光子处理上， 先采用期望值估计(expect value estimator， EVE)产光， 分别统计原级线光子和原级连续光子对探测器的直穿贡献. 为了避免EVE产生的大量小权光子模拟带来的计算量和存储量的增加， 做完直穿贡献后， 光子历史结束， 立即回到原来的直接估计(direct estimator， DE)产光模式， 每次最多产生一个光子， 对其进行跟踪，只记录散射贡献， 这样在不增加计算存储量下， 实现了特征γ射线解谱.

2 问题描述

高能中子与核发生非弹(用(n， n' )表示)和俘获(用(n， γ)表示)反应时， 将产生次级光子， 用次级光子的特征γ射线来确定客体的核素组成和份额， 这是核探测相对X光探测的优势所在. 辐射俘获是吸收反应中最重要的反应之一， 其反应产物之一就是γ射线， 产生次级光子的主要反应道有(n， γ)和裂变(用(n， f )表示). 如果中子源的能量和强度较高， 则中子与核发生(n， n' )反应的概率增大， 并产生非弹γ射线. 表1给出H， C， N等11种核素发射非弹γ谱线和俘获γ谱线的能量[13]，表2给出烈性炸药(TNT)和某些化学武器中所含元素的重量百分比[13].

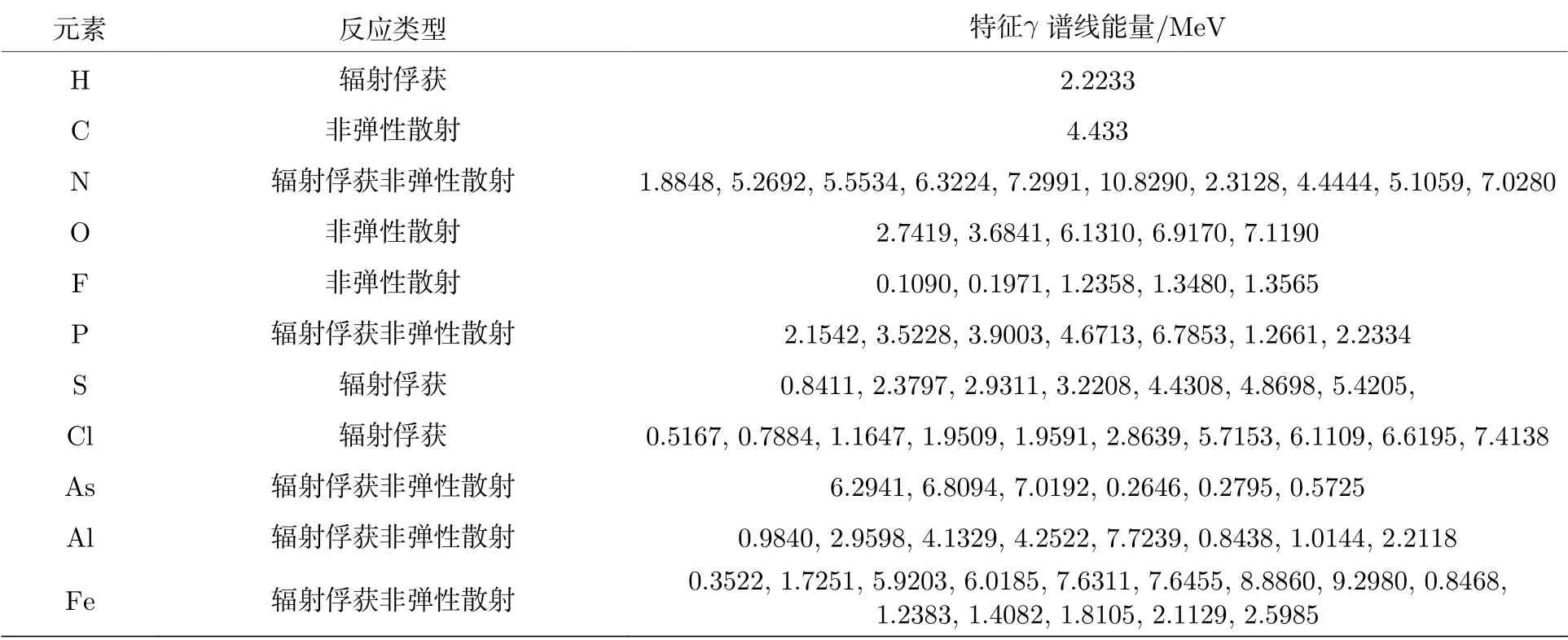
表 1 H， C， N， O等核素发射俘获γ谱线和非弹性散射γ谱线能量Table 1. Energy of spectrum line from inelastic γ and capture γ about H， C， N， O， etc.

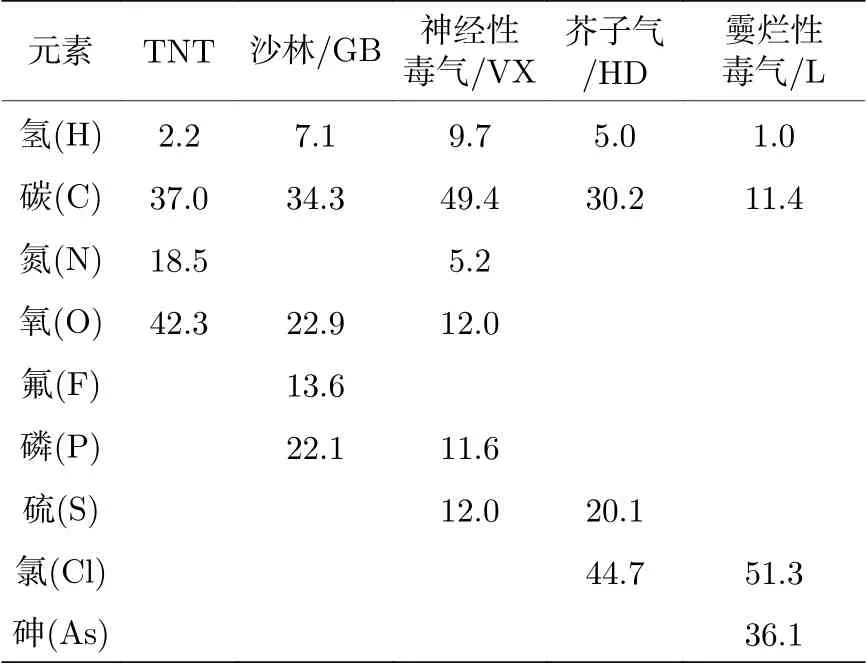
表 2 烈性炸药(TNT)和某些化学武器中所含元素的重量百分比Table 2. Weight percentage of elements in some spirited detonators (TNT) and chemical weapons.

2.1 非弹γ和俘获γ时间门测量方法

对于某些问题， 需要通过发射脉冲源， 通过时间箱计数来区别非弹γ射线和俘获γ射线， 图1给出放射性石油测井中， 碳氧比(C/O)能谱测井的定时测量图[14-16]. 用脉冲方式发射中子， 通常0—10 μs为脉冲门发射时间间隔， 10—20 μs为本底门时间间隔， 20—90 μs为晚俘获门时间间隔，依据这种逻辑关系， 可以得到: 净非弹γ计数=脉冲门谱计数—本底谱计数; 俘获γ计数=晚俘获门计数. 这个时间门测量过程同样适合其他含时核探测问题的模拟.

对应图1给出不同时间门下探测器脉冲高度谱计算公式. 设Nδ(E， t)为以δ(t)脉冲方式发射的E0= 14.1 MeV氘氚中子源探测器中测到的γ能谱的时间响应. 根据中子-光子输运方程的线性性质， 对应于任意时间分布S(t)的中子源， 探测仪中测到的γ能谱时间响应为

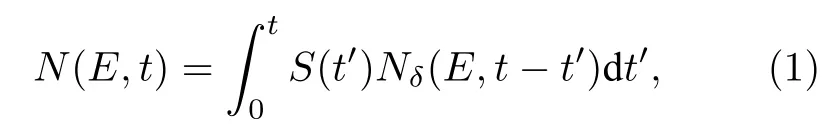
其中E表示能量， 单位MeV; t表示时间， 单位μs.

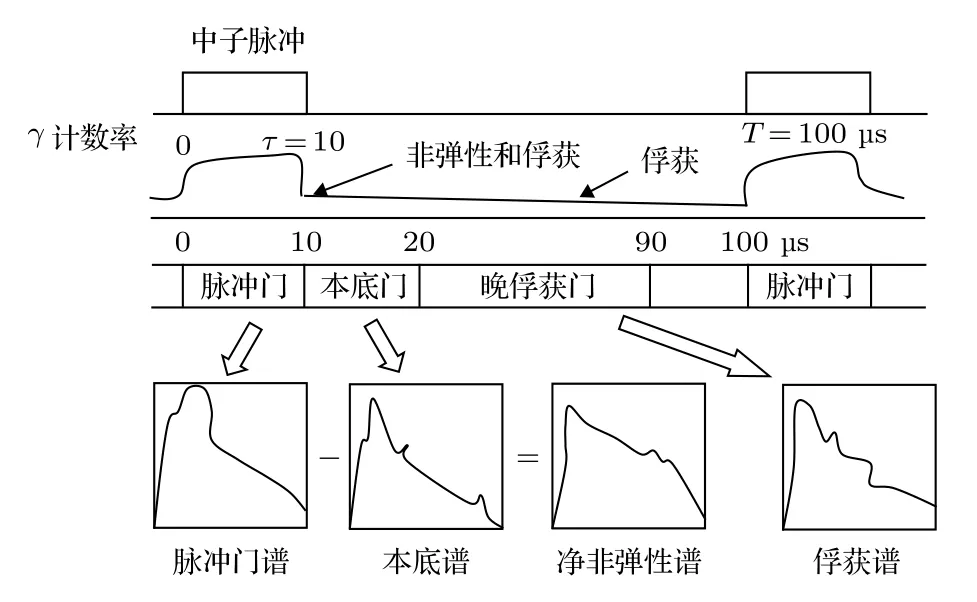
图 1 碳氧比测井中子引发非弹性散射γ与俘获γ定时逻辑图Fig. 1. The timing diagram of neutron induced inelastic γ and capture γ in C/O well-logging.

在任意测量门[ta， tb]内记录的γ能谱为

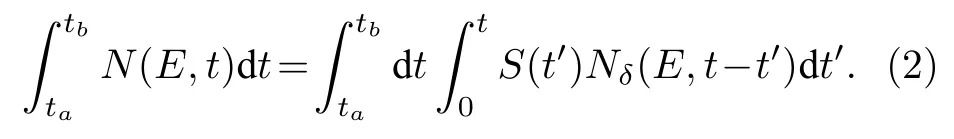
令中子脉冲时间分布函数S(t)为周期函数，其周期为τ， 有

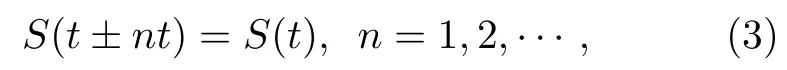
其中t∈[0， τ]. 又假定S(t)为宽度为τ的函数

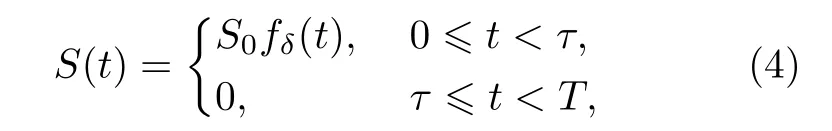
其中S0为一个脉冲内释放的中子总数; T为终态时间; fδ(t) 为脉冲时间分布函数， 满足归一条件. 则有

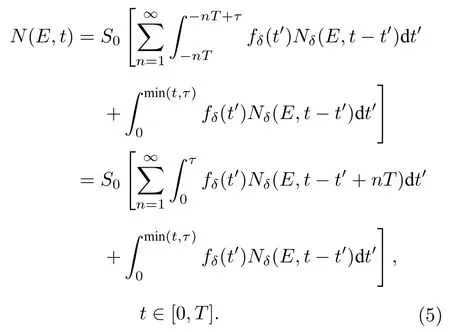
将(5)式代入(2)式， 对t积分便得任意时间门内的γ能谱强度.

脉冲门内的测量值为

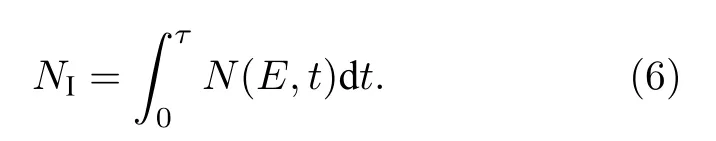
本底门内测量值为

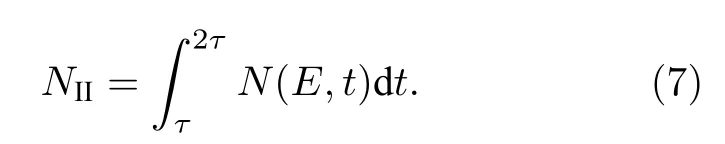
根据中子进入客体诱发的各种γ射线的时间特点， 将(5)式中的Nδ(E， t)分解为4个部分， 即

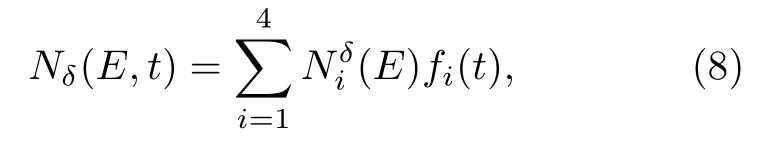
其中 Niδ(E)，i=1，2，3，4 分别为单位强度δ(t)脉冲中子源引起的非弹性γ射线、慢化过程中的俘获γ射线、热中子俘获γ射线和活化反应γ射线的γ能谱强度; fi(t)， i = 1， 2， 3， 4分别为上述4种γ射线的时间谱， 满足归一条件1， 2， 3， 4).

经过一系列公式推导， 得到脉冲门能谱

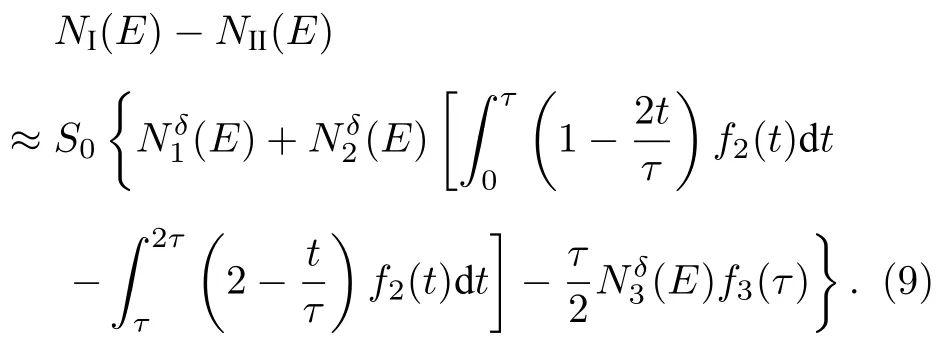
可见脉冲门与本底门测量值之差除了非弹性γ能谱， 还受到少量慢化过程俘获γ射线和少量未扣除干净的热中子俘获γ谱的“污染”. 考虑到活化γ射线的发射时刻很晚， 加之活化γ射线的发射寿命≫T . 因此， 在脉冲门与本底门谱之差中， 活化γ射线的污染是很小的. 另外， 由于慢化过程中的中子俘获数目远远小于热中子俘获的数目， 所以，N3δ(E)≫N2δ(E) ， 可以认为污染源主要来自热中子俘获γ射线， 其中污染量大小除与中子源的特征及客体物理性质有关， 探测仪器材料的适当选择也起一定的作用.

要准确算出探测器响应的测量能谱N(E， t)，首先应设法算出Nδ(E， t)， 然后与中子源脉冲时间谱形fδ(t)卷积， 并分别对两个测量门的时间间隔积分， 相减后得到. 因此， MC模拟的关键是算出t时刻单位强度δ-脉冲源相应的探测器计数Nδ(E， t)， 然后与给定的中子脉冲谱形函数fδ(t)卷积，再对指定的时间门积分， 得到任意时间门内的测量 值.

2.2 N(E， t)的MC模拟

快中子非弹性散射， 它所要测量的是非弹性γ射线. 理论上通过解中子-光子-电子耦合输运求出N(E， t). 由于探测器相对整个问题系统很小， 尽管从源发出了大量的中子， 但能够进入探测器的次级光子数还是非常有限的， 依据少量的次级光子要算准探测器响应几乎是不可能的. 因此， 探测器响应-脉冲高度谱计算通常分三步进行.

第一步: 解中子-光子耦合输运方程， 求出进入探测器表面的次级γ流，

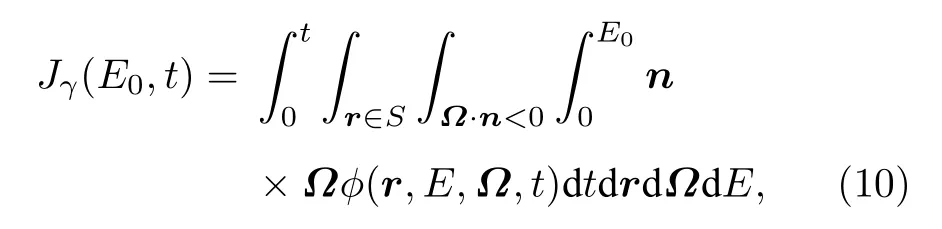
其中S为探测器表面， n为探测器表面外法向矢量， E0为入射光子能量.

第二步: 解光子-电子耦合输运方程， 求出探测器响应函数R(E0， h). 以碘化钠闪烁探测器为例，其响应函数形式为

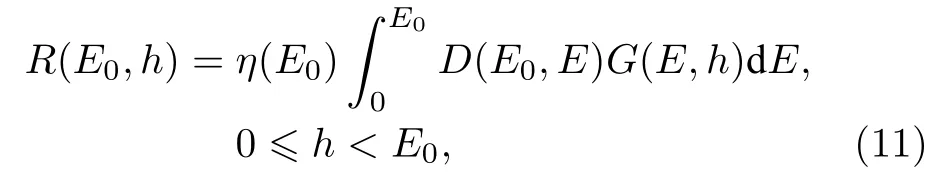
其中 G (E，h) 为 高斯函数; D (E0，E) 为能量沉积谱;η(E0) 为探测器效率; h为能量道， 单位MeV. 由于响应函数中含有高斯函数G， 为了保证求积精度，分点要足够多， 通常在全能区[0， Emax]分256道.根据Berger等[17]和Jin等[18]的研究， 不同入射方向的光子对探测器响应影响很小， 因此， 方向可近似为各向同性， 当探测器形状及材料一定后，响应函数R(E0， h)(矩阵形式)只需计算一次.

第三步: 卷积积分得到探测器响应脉冲高度谱

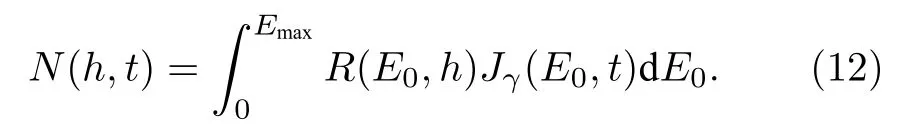
N(h，t) 求解涉及瞬态中子-光子-电子耦合输运计算， 计数包括时间-能量联合谱， 是MC粒子输运计算 中难度最大， 模拟最复杂的过程.

2.3 特征γ射线标识计数

中子发生非弹(n， n')或俘获(n， γ)， (n， f )反应时， 将产生次级光子， 这些光子统称为特征γ射线. 根据次级光子能量特征， 特征γ射线分为原级线光子和原级连续光子， 其定义如下:

其中i为核; j为反应道; En为中子发生非弹或俘获反应时的能量; 通常取Eline= 0.001 MeV作为原级线光子和原级连续光子的分界能量; LP为ENDF数据库反应律序号；Ai为碰撞核i的原子序数；EG(i)为特征γ能量.

LP ≠ 2对应的γ原级线光子， 它不随入射中子能量变化， 是甄别客体核素组成的核心关键. 在表1中给出了主要核素γ谱线能量峰位置， 表2给出烈性炸药(TNT)和某些化学武器中所含元素的重量百分比[13]， 依据表1和表2所列参考值， 可以快速识别出客体是否为危禁品. MCNP程序模拟次级光子时， 没有把这两类光子区别开来， 因此，次级光子能谱中的一些特征γ峰会被散射能谱磨平， 无法确定客体的核素组成.

当前ENDF最新评价核数据库提供了两种中子产光子模式: 1) 30 × 20产光模式， 中子从10—5eV到20 MeV分30个能群， 每个中子群对应20个等高度谱线， 次级光子的发射方向按各项同性处理;2)按碰撞核对应反应道的产光概率产光子. 模拟采用第2)种产光模式.

2.4 EVE产光

设中子与i核发生j种反应的产光概率为pi，j(j = 1， 2， ···， J )， 满足归一条件， 这里J为i核对应的反应道总数.

DE方法已知i， 抽随机数ξ， 求出满足不等式的j， 则j反应道产光， 光子权重为wγ.

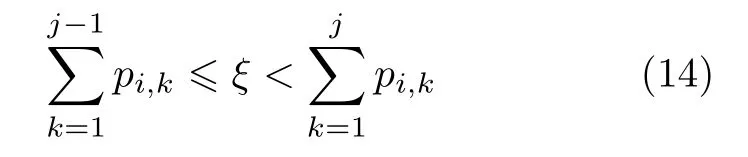
EVE方法已知i， 按概率pi，j(j = 1， 2， ···，J )全部产光， 相应光子权重为

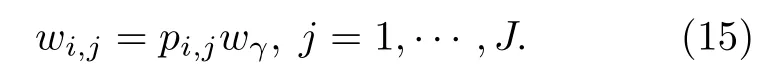
不难证明两种估计方法的数学期望是一致的.DE存在随机因素， 某些小概率大贡献事件会因为随机因素少抽或漏抽， 这对隐藏爆炸物探测这类问题是不允许的. 故采用EVE是必要的. 我们早期开发研制的MCCO程序， 对EVE产出的光子进行全部跟踪， 用统计估计计数[19]， 增加了大量计算存储量. 考虑到特征γ射线探测主要关心的是次级光子的直穿贡献， 实际上跟踪所有小权次级光子的散射过程没必要. 为此， 我们设计了现在的组合产光模式.

组合产光模式对EVE产生的大量小权光子， 仅做直穿估计， 之后回到原来的DE产光， 每次最多产生一个次级光子， 对该光子进行全程跟踪， 只统计散射贡献， 最后的数值模拟解由两部分组成， 即

由于直穿估计可以解析计算， 所花时间可以忽略不计. 因此， 采用组合产光模式后， 实现了特征γ射线能量-时间解谱， 而总计算时间和存储量增加很少.

3 数值实验

炸药球模型几何单位为cm， 对行李箱进行安检. 如图2所示， 设行李箱长、宽、高分别为80， 30，50， 内放一半径为3.51， 密度为ρ = 1.654 g/cm3的RDX炸药小球(分子式为C2.63H4.69N0.658O0.85);探测器位于行李箱上方， 为3'' × 3''碘化钠闪烁晶体正圆柱探测器， 密度为ρ = 3.67 g/cm3， 柱中心坐标为(0， 0， 38.75); 采用14.1 MeV各项同性氘氚中子点源， 源位置为(0， 45， 0)， 计算进入探测器的次级γ流Jγ(E， t). 采用源方向偏倚发射， 偏倚立体张角覆盖行李箱. 对比程序选择MCNP[1]， 采用相同的数据库、样本数和源方向偏倚技巧.

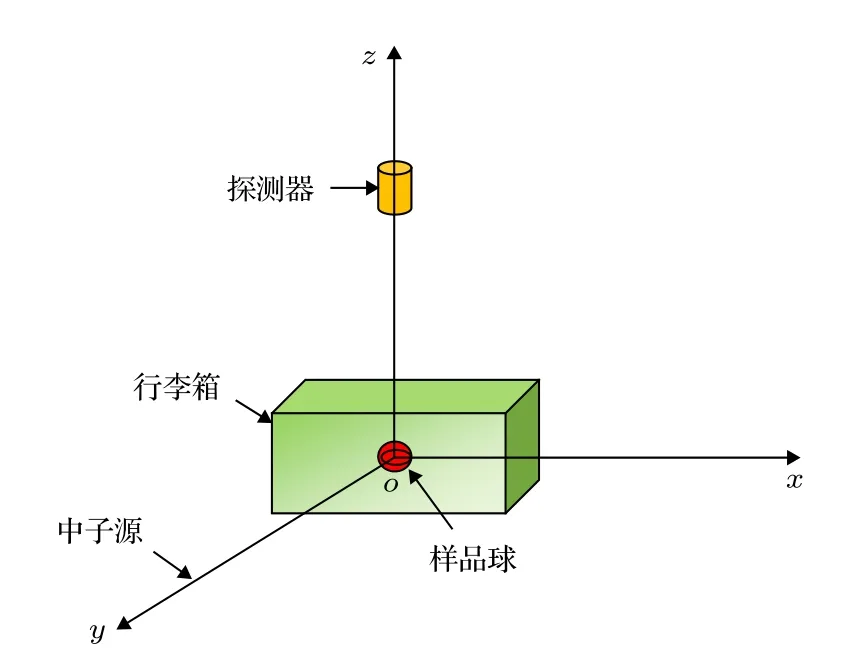
图 2 行李箱模型示意图Fig. 2. Sketch of luggage model.

表3给出JMCT与MCNP探测器次级光子流Jγ结果比较; 表4给出JMCT统计的箱子内的核素组成及份额， 与表1给出的TNT炸药H， C，N， O核素百分比基本相符(炸药类型不同); 图3(a)和图3(b)分别给出原级线光子和康普顿散射光子能谱; 图3(c)和图3(d)给出JMCT与MCNP次级γ流的能谱比较， 可以看出次级γ总流JMCT与MCNP结果符合良好， 能谱差异很小; 图4给出次级γ流时间谱， JMCT与MCNP时间谱总计数相符， 时间谱细节上有些差异， 分析原因是由于时间箱分得过细， 某些时间箱计数的统计误差偏大.

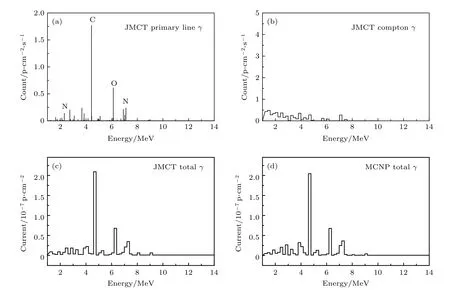
图 3 次级γ射线能谱计算结果比较 (a)次级γ原级线光子能谱; (b)原级连续光子与Compton散射能谱; (c) JMCT次级γ总能谱; (d) MCNP次级γ总能谱Fig. 3. Comparison of calculated result about energy spectra of secondary γ: (a) JMCT primary line γ; (b) JMCT Compton γ;(c) JMCT total γ; (d) MCNP total γ.

表 3 JMCT与MCNP次级γ流计算结果比较Table 3. Comparison of calculated results about secondary γ between JMCT and MCNP.

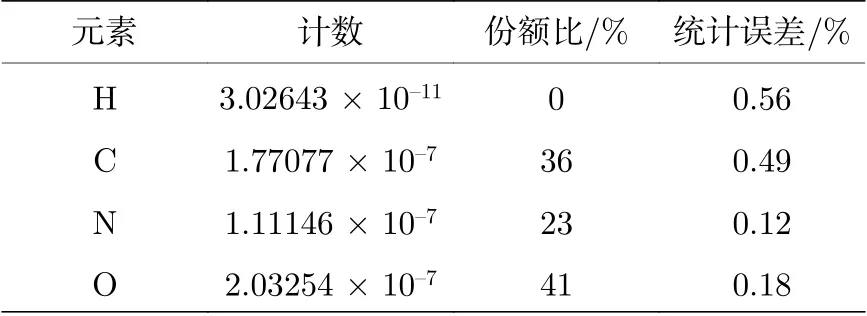
表 4 H， C， N， O瞬发γ计数及份额Table 4. Count and percentage of prompt γ from H， C， N and O.

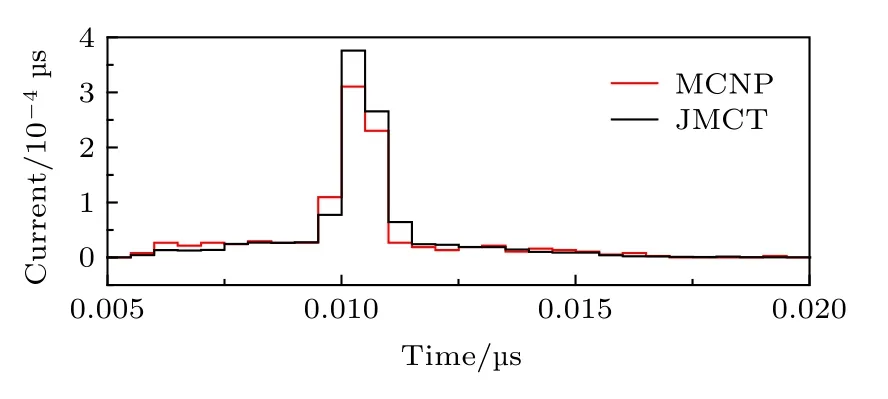
图 4 JMCT与MCNP次级γ流时间谱比较Fig. 4. Comparison of secondary γ-fluent tine spectrum between JMCT and MCNP.

4 结 论

基于JMCT程序开发了特征γ射线能量-时间联合谱计算功能， 数值实验初步验证了软件计算的正确高效性. 目前已开展了数十种炸药模型的计算， 构建了相应的数据库， 为反演计算做准备. 后续将配合实验样机的研制， 对测量仪器进行刻度工作， 形成能快速做出判断的计算机软件正演/反演系统， 为在线检测提供理论技术支持.