柱形汇聚几何中内爆驱动金属界面不稳定性*

王 涛，汪 兵，林健宇，钟 敏，柏劲松，李 平，陶 钢

（1. 中国工程物理研究院流体物理研究所，四川 绵阳 621999；2. 南京理工大学能源与动力工程学院，江苏 南京 210094）

当冲击波或惯性力加载不同物质间的扰动界面时，界面会失稳并发生扰动增长的现象，前者称为Richtmyer-Meshkov（RM）不稳定性[1-2]，后者称为Rayleigh-Taylor（RT）不稳定性[3-4]。其中RT 不稳定性与加载方向有关，只有当轻介质加速重介质时才会发生。界面不稳定性在诸多领域有重要的应用背景，如惯性约束聚变[5-6]、超新星爆炸[7]、小行星撞击[8-9]、地球内核运动及板块构造[10-11]等，因此具有重要的研究意义。

Wang 等[12-18]、Bai 等[19-21]、Xiao 等[22]长期研究流体介质界面不稳定性及湍流混合演化规律和统计特性。Liu 等[23]通过直接数值模拟，研究了RM 不稳定性和湍流混合中的能量传递过程和机制。李俊涛等[24-25]也通过数值模拟，研究了弱冲击波加载V 形界面导致的RM 不稳定性中的涡动力学行为特性及作用机制。Luo 等[26-27]、Si 等[28]、Ding 等[29]、Lei 等[30]在汇聚冲击波诱导下的气体界面不稳定性实验研究方面成绩卓越，特别是首次测得了柱形单模态air/SF6界面的扰动振幅。在我国，有关界面不稳定性的研究主要集中在流体介质方面，很少涉及金属材料界面不稳定性，而界面不稳定性也会在金属材料中发生。而且，金属材料的复杂物性，如强度、相变、损伤、微结构等，使金属材料界面不稳定性比流体界面不稳定性更复杂，因此，金属材料界面不稳定性是一种跨尺度多物理耦合的复杂流动问题。

金属材料界面不稳定性的理论研究，主要基于能量平衡[31-33]或力平衡[34-36]，推导扰动增长所满足的色散关系，但是，这些线性理论分析均采用了理想塑性本构关系，预测扰动增长受到较大限制。我们也基于能量平衡，但采用了Steinberg-Guinan（SG）和Johnson-Cook（JC）本构模型及变压力加载历程，针对有限厚度金属平板问题，推导了相应的扰动增长方程，将线性分析方法进行了拓展，可用于平面几何金属不稳定性线性和非线性段增长的预测[37]。并且，对爆轰驱动和激光等离子体驱动的金属界面不稳定性实验进行了分析，结果和实验吻合较好，但是，这种线性分析方法依然有较大的局限性，如它还无法考虑加载过程等。

金属材料界面不稳定性实验研究始于20 世纪70 年代。首先，由Barnes 等[38-39]通过爆轰驱动铝平板实现，并采用高能X 射线装置观察界面扰动增长。后来，平面爆轰驱动金属材料界面不稳定性实验[40-42]均采用相似的装置。在美国、俄罗斯，开展了大量有关金属材料界面不稳定性的研究工作，包括界面扰动增长规律及影响因素的研究等。何长江等[43]通过数值模拟，研究了初始扰动波长对平面爆轰驱动金属铝RT 不稳定性发展的影响。郝鹏程等[44]、刘军等[45]通过对内爆加载金属钢壳的数值模拟，研究了材料强度和初始波长对界面扰动增长的影响。Olson 等[46]在爆轰实验中，研究了铜材料的微结构和加工对RT 扰动增长的影响，发现单晶晶向和材料加工导致的应变硬化会影响扰动增长，而多晶材料的晶粒尺寸和晶界强化在所研究的加载条件下对扰动增长无影响。Jensen 等[47]采用高分辨率的原位诊断技术，研究了冲击条件下铈的RM 不稳定性问题。Cherne 等[48]采用分子动力学模拟方法，研究了铜样品自由面上不同形状的二维沟槽扰动对铜/真空界面RM 不稳定性发展的影响。

金属材料界面不稳定性增长是一种高压高应变率条件下的大变形行为，与材料强度密切相关，宏观表现就是材料强度可以抑制扰动增长。近几年，基于这个思想，利用金属材料界面不稳定性增长，研究高压高应变率条件下的材料强度[42,49-53]，进而发展了适用性更强的材料强度模型[54]。

由以上分析，目前对于金属材料界面不稳定性问题，虽然已经开展了较多的研究，但是还不充分不深入，仍然有很多问题有待解决。比如，理论研究很不完备，实验研究缺乏对物理细节的直接认识，而且高分辨率诊断设备和极端加载装置限制了实验工作的全面开展。因此，数值模拟成为一种有效便捷的研究手段。我们长期致力于流体界面不稳定性及湍流混合问题的数值模拟研究[12-22]。在此基础上，我们发展了适用于金属材料大变形行为数值模拟的高保真度爆轰与冲击动力学欧拉程序。本文中，利用自研的数值模拟欧拉程序，研究柱形汇聚几何中内爆驱动下金属材料界面不稳定性的动力学行为。

1 计算方法

针对考虑爆轰和材料弹塑性行为的多物质、大变形及强冲击波物理问题，发展了高保真度的爆轰与冲击动力学欧拉有限体积计算程序。其守恒型控制方程组为：

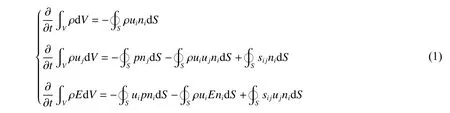
式中：下标i、j 分别代表x、y、z 三个方向，遵循张量运算法则，V 为控制体体积，S 为控制体表面积，ni为其外法向单位矢量分量，ρ、uk(k=i, j)、p、E 分别为密度、速度、压强和质量总能量，sij为偏应力张量分量。

采用维数分裂技术，将方程组（1）描述的物理问题分解为多个一维问题，对于每个一维问题，采用PPM 方法，对单元内物理量的分布进行插值和重构；然后，通过欧拉型两步算法进行计算，即物理量的Lagrange 推进求解，再将拉氏网格上的物理量映射到静止的欧拉网格上。材料强度效应、炸药爆轰过程和人工黏性在Lagrange 步中实现。多物质界面采用体积分数方法进行捕捉。

1.1 状态方程

数值模拟中，炸药用JWL 状态方程描述：

E=ρ0E′E′

式中：相对比容V=ρ0/ρ，A、B、R1、R2、ω 为常数， 为体积内能， 为比内能，cV为比热。

金属材料用Mie-Grüneisen 状态方程描述：

式中：相对压缩度 µ =ρ/ρ0−1 ，ρ0为初始密度，c 为零压声速，γ0为Grüneisen 系数，a、S1、S2、S3为常数。

硅橡胶采用凝聚介质实用状态方程：

式中：c0为正常态的声速，γ 为材料参数。

1.2 本构方程

金属材料采用SG 本构模型，它可以很好地描述高压高应变率下的材料强度特性。SG 本构模型在弹塑性本构方程中引入压力、温度和应变率项，同时压力与应变率对流动应力的耦合效应具有可分离变量特性。因为SG 本构模型中流动应力依赖于压力，所以材料的本构方程与状态方程之间存在某种耦合关系。这个耦合关系反映了高压下金属材料的压力硬化特性。SG 本构模型的动态屈服强度和剪切模量分别为：

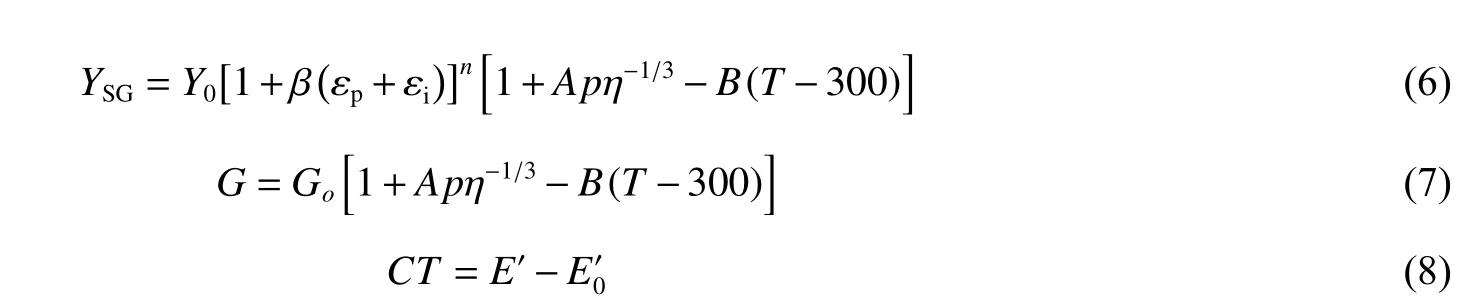
式中：Y0和G0分别为初始屈服强度和剪切模量，β 和n 分别为材料应变硬化系数和硬化指数，A 为压力硬化系数，η=ρ/ρ0为材料压缩比，B 为温度软化系数，为零温下的比内能，C 为材料常数。

2 结果与分析

在进行柱面内爆驱动不锈钢金属材料界面不稳定性计算和分析前，先通过对文献[40]中的爆轰驱动T-6061 铝的RT 不稳定性实验的模拟，确认本计算程序的可靠性。该实验采用HMX 炸药爆轰加载1.5 mm 厚的铝样品，加载压力峰值为30 GPa。初始扰动波长λ0=2 mm，初始扰动振幅a0=0.15，0.11 mm。图1 为用自研的欧拉程序计算得到的扰动振幅和文献[40]中采用ARES 程序计算的结果，及实验结果（横轴是自由面运动位移）。可以看出，数据吻合较好，说明自研的欧拉程序模拟这类爆轰驱动金属材料界面不稳定性是准确的。

图 1 爆轰驱动铝实验的扰动振幅Fig. 1 Perturbation amplitudes of experiments driven by explosion

2.1 柱面内爆计算模型和参数

以Frachet 等[55]的柱面内爆驱动不锈钢金属材料的双模态扰动界面不稳定性实验为基础，开展柱面内爆驱动下金属材料界面不稳定性发展演化的动力学行为特性数值模拟。

计算模型如图2 所示：外层为炸药，其外直径和厚度分别为200 和50 mm，由于文献[55]中没有说明何种炸药，本文中采用TNT；中心物质为直径92 mm 的硅橡胶；中间不锈钢壳外直径为100 mm，厚度为4 mm，且内界面上预置有振幅0.5 mm、模数为13 和29 mm−1的双模态初始扰动。

T N T 炸药J W L 状态方程参数分别为：ρ0=1.63 g/cm3，pcj=21.0 GPa，Dcj=6.93 km/s，A=371.2 GPa，B=3.231 GPa，R1=4.15，R2=0.95，ω=0.3。不锈钢Mie-Grüneisen 状态方程参数分别为：ρ0=7.896 g/cm3，c=4.569 km/s，γ0=2.17，a=0.47，S1=1.49，S2=S3=0；不锈钢SG 本构模型参数分别为：Y0=0.34 GPa，Ymax=2.5 GPa，G0=77.0 GPa，β=43.0，n=0.35，A=0.022 6 GPa−1，B=0.455 kK−1。硅橡胶凝聚介质实用状态方程参数分别为：ρ0=1.15 g/cm3，c0=1.343 km/s，γ=1.6。

图 2 柱面内爆驱动金属材料界面不稳定性计算模型Fig. 2 Computational model of metal interface instability driven by cylindrical implosion

2.2 加载和界面运动特性

冲击波(SW)由低阻抗介质向高阻抗介质方向加载物质界面时，会产生一个透射冲击波和一个反射冲击波；冲击波由高阻抗介质向低阻抗介质方向加载物质界面时，会产生一个透射冲击波和一个反射稀疏波(RW)。炸药起爆后，产生的柱形爆轰波向内聚心运动，到达钢壳外界面并作用后，向内产生透射冲击波，钢壳也开始聚心运动，由于质量守恒，钢壳径向厚度逐渐增大（见图3）；该透射冲击波约在7.8 µs时到达钢壳内界面，形成由高阻抗介质向低阻抗介质方向的冲击波加载，内界面加载压力瞬间达到10 GPa（见图4），同时向硅橡胶内产生透射冲击波和钢壳内的反射稀疏波；钢壳内的反射稀疏波向外运动并加载外界面后又向内反射压缩波(CW)，压缩波和稀疏波会在钢壳内多次反射，并在内外界面上分解而交替产生稀疏波和压缩波，进而交替加载钢壳界面，可见于钢壳内三角形的胞格结构（见图3）、加载压力和内界面速度振荡区域（冲击波加载和稀疏波卸载效应）（见图4、5，界面运动速度以径向向外为正）；硅橡胶内的透射冲击波聚心反弹后，在约20.5 µs 时到达并冲击(RS)钢壳内界面，内界面加载压力瞬间达到约50 GPa，钢壳聚心运动停止，开始向外反弹运动，其径向厚度之后又逐渐减小，并向硅橡胶内反射冲击波和向钢壳内透射冲击波，该反射冲击波会再次聚心反弹加载，但已不在本算例时间内，而钢壳内的透射冲击波也会在内外界面上分解而交替产生压缩波和稀疏波。

由从钢壳内界面运动速度（见图5）和加速度剖面（见图6）看出，内界面首次受到冲击加载后扰动开始反相（峰谷转换），发生RM 不稳定性，接着又受到三次有效的向心反射压缩波加载，在约12 µs 前，虽然有轻介质加速度重介质的RT 不稳定性，但以RM 不稳定性为主导。在12 µs 到冲击波聚心反弹加载前，由于中心区域压力的升高，界面聚心运动加速减速，扰动发展由轻介质加速重介质的RT 不稳定性主导。冲击波聚心反弹加载后及之后内界面受到四次有效的向心反射稀疏波加载，扰动发展由RM 不稳定性主导。

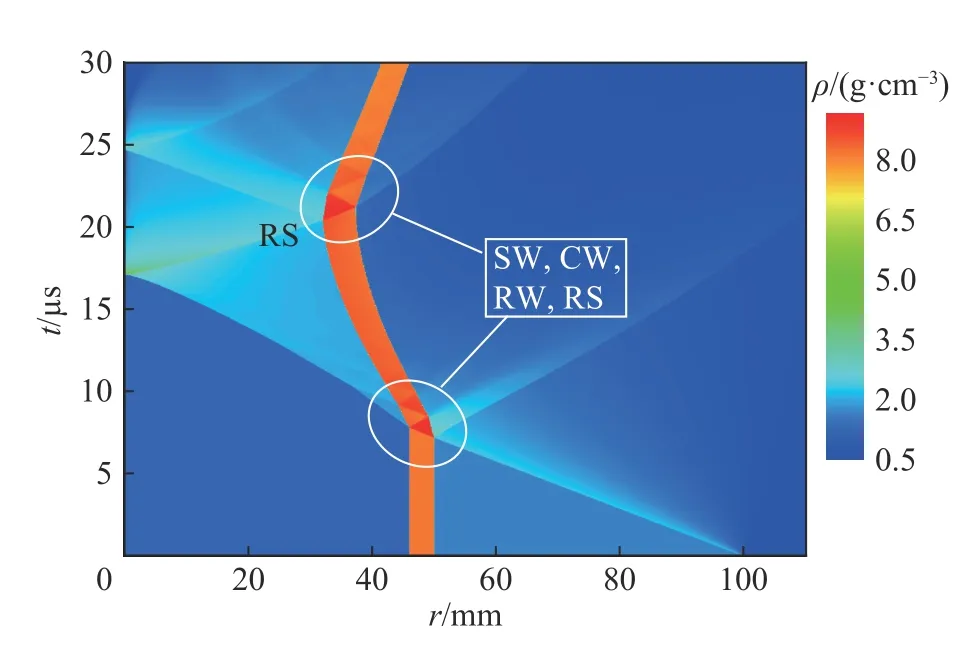
图 3 密度显示的一维波谱图Fig. 3 One dimensional wave diagram displayed by density

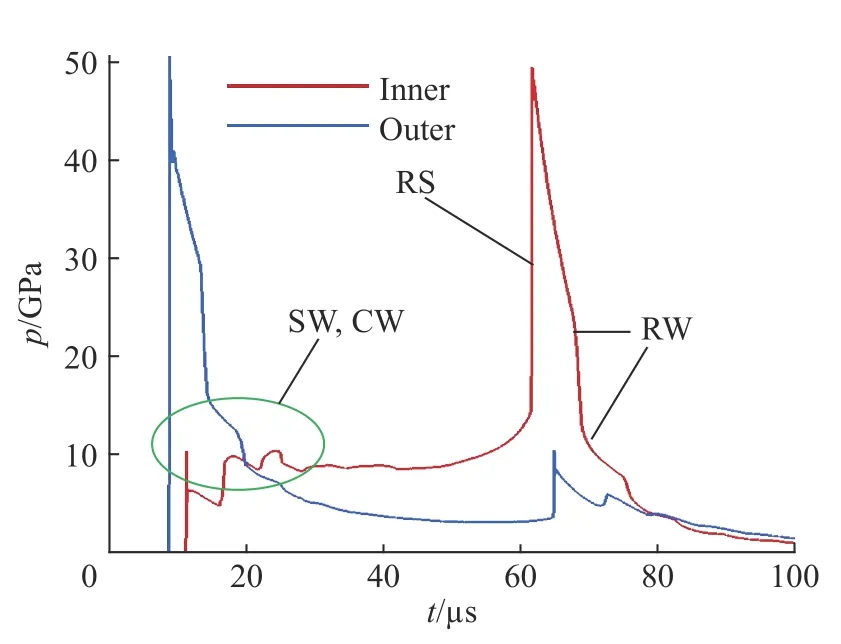
图 4 不锈钢壳内外界面加载压力Fig. 4 Loading pressures on inner and outer interface

图 5 不锈钢壳内界面运动速度Fig. 5 Velocity of inner interface

图 6 不锈钢壳内界面加速度Fig. 6 Acceleration of inner interface

2.3 扰动界面演化

图7 为不同网格分辨率（146、73、36 µm）下钢壳内界面双模态扰动各模态（模数13 和29 mm−1）振幅增长过程，粗网格与中等网格、中等网格与细网格结果的最大相对误差分别为3%、1.5%，满足收敛要求，所以计算中采用36 µm 的网格。
图8 为5、10、15、20、25 µs 时密度场图像，显示了钢壳在内爆冲击波和聚心反弹等加载下的运动过程和内界面扰动演化过程。图9 为17.8、22.8 和25.3 µs 时钢壳内界面扰动演化的实验图像和数值模拟图像。图10 为对双模态扰动演化做谱分析得到的0、10、15、20、25 和30 µs时各模态的扰动振幅，在多次冲击加载下，所有模态都被激发，但主导界面演化的还是模数13 和29 mm−1两个模态。图11 为双模态扰动振幅增长历史，数值模拟结果和实验差别较大，原因是文献[55]中并没有说明内爆采用的是何种炸药，而本模拟中采用TNT，TNT 爆炸后加载在钢壳上的压力和文献[55]中的压力有较大差别。由图11 还可看出：低模数扰动增长比高模数扰动增长速度快，这与纯流体情况刚好相反，是由金属材料弹塑性机制导致；而且，对于低模数扰动，在扰动反相后至冲击波聚心反弹加载前，扰动振幅以近似线性规律增长，而高模数扰动由于较强的非线性作用，非线性增长规律明显。

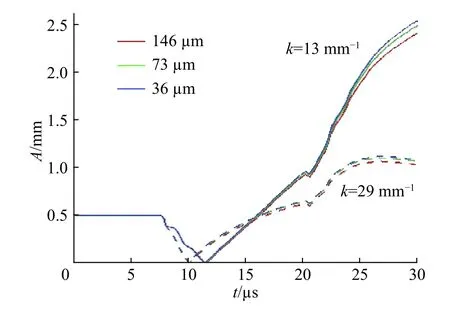
图 7 网格收敛性分析Fig. 7 Grid convergence

图 8 密度场Fig. 8 Images of density fields

图 9 钢壳内界面的扰动Fig. 9 Inner perturbed interface of steel shell

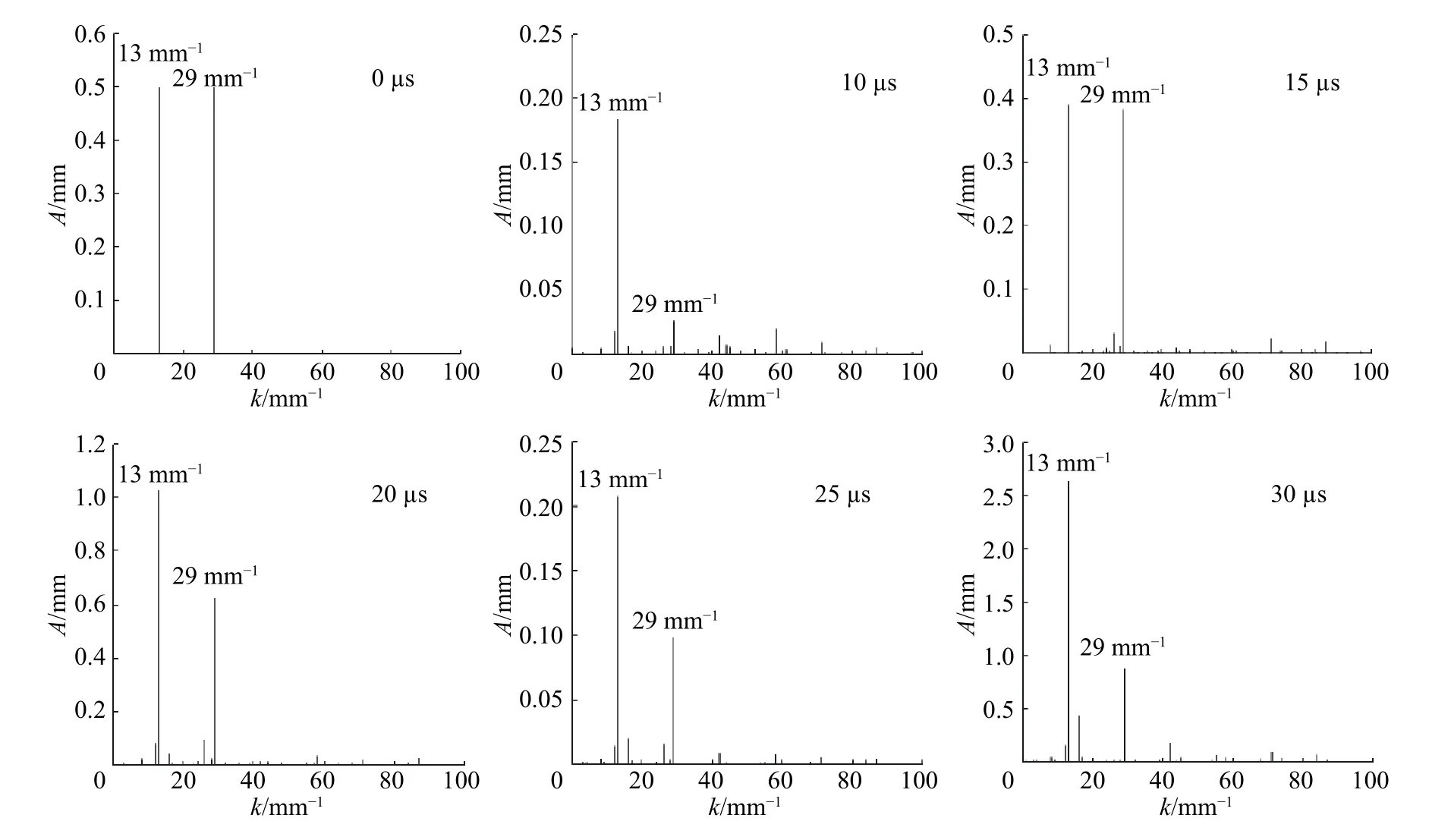
图 10 双模态扰动演化的谱分析Fig. 10 Spectral analysis of dual mode perturbation evolution

图 11 双模态扰动的振幅增长曲线Fig. 11 Amplitude growth curves of dual mode perturbation

2.4 初始扰动振幅、波长、钢壳厚度和几何特性的影响

本节主要研究初始扰动振幅、波长、钢壳厚度和几何特性对柱形内爆驱动下钢壳内界面扰动增长的影响。

首先，研究初始扰动振幅的影响。保持初始扰动模数为13 mm−1，初始振幅分别为0.05、0.10、0.25、0.50、0.75 和1.00 mm。图12 为不同初始扰动振幅时的振幅增长，较大的初始振幅意味着较大的振幅增长，而且扰动反相的时间与初始振幅无关。

其次，研究初始扰动波长的影响。保持初始振幅为0.5 mm，初始扰动的模数(波长的倒数)分别为13、16、20、24、29、35、40、45、50、56、60 mm−1。图13 为不同初始扰动模数时的振幅增长，高模数（小波长）扰动反相时间明显比低模数（大波长）扰动反相时间短，即扰动反相时间与扰动模数相关。反相后高模数扰动振幅增长速度比低模数扰动振幅增长速度快，但是低模数扰动振幅会以该速度近似线性增长，直至聚心反弹冲击波加载时截止；而高模数扰动振幅增长速度会逐渐减小，其振幅及增长速度会小于低模数扰动；而且，随着初始扰动模数的增大，振幅增长在后期会停止，说明柱形内爆驱动金属材料界面不稳定性增长存在截止波长。

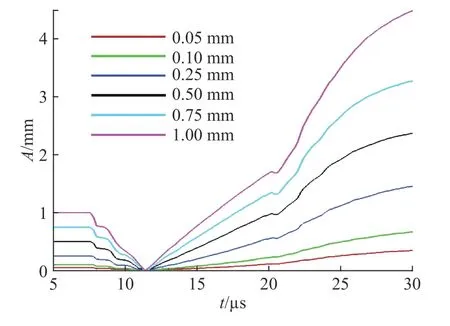
图 12 不同初始扰动振幅时的振幅增长曲线Fig. 12 Amplitude growth curves for different initial perturbation amplitude

图 13 不同初始扰动模数时的振幅增长曲线Fig. 13 Amplitude growth curves for different initial perturbation mode number

接着，研究钢壳初始厚度的影响。初始扰动模数分13 和60 mm−1两种，初始振幅均为0.5 mm，初始厚度分别为4、7 和10 mm。图14 为不同钢壳初始厚度时振幅增长情况：随着钢壳初始厚度的增大，扰动振幅增长速度逐渐减小；而且，对于模数为60 mm−1的初始扰动，不同厚度时的扰动振幅几乎相同，后期增长也趋于停止，即钢壳厚度会抑制扰动增长，而且存在一个截止厚度。

最后，研究几何特性对冲击驱动钢壳界面不稳定性增长的影响。保持初始时刻的炸药厚度、钢壳厚度、硅橡胶厚度、扰动振幅和模数均相同的情况下，分为柱形汇聚几何和平面几何构型。初始振幅为0.5 mm，模数为13 mm−1。图15 为不同几何构型下的振幅增长情况，汇聚几何构型下的扰动振幅比平面情况下大，这可以由两种情况下界面运动速度(见图16)和界面加速度(见图17、6)解释。首先，几何汇聚带来几何收缩效应（BP 效应），由于能量汇聚使加载压力较大，界面加速运动较快，因此扰动增长速度也较快；其次，当界面运动减速时，几何收缩会造成界面加速减速，而平面情况下界面是减速减速，因此减速运动阶段的RT 不稳定性发展在汇聚情况下更剧烈；再者，汇聚情况下冲击波聚心反弹加载时间早于平面情况，而且反弹加载强度也较大，因此之后的RM 不稳定性发展在汇聚情况下也更剧烈。所以，整体上汇聚几何中界面不稳定性发展速度快。

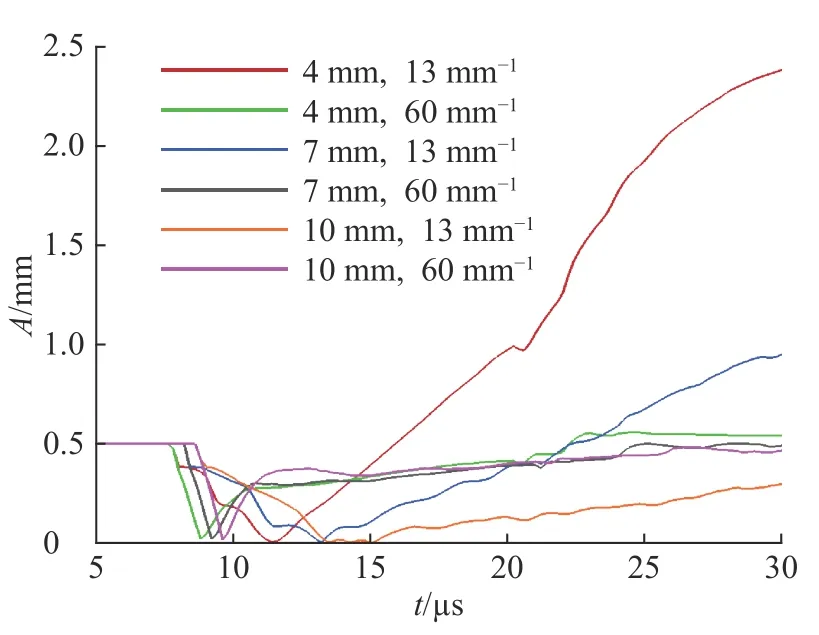
图 14 不同钢壳初始厚度时的振幅增长曲线Fig. 14 Amplitude growth curves for different initial thickness of steel shell

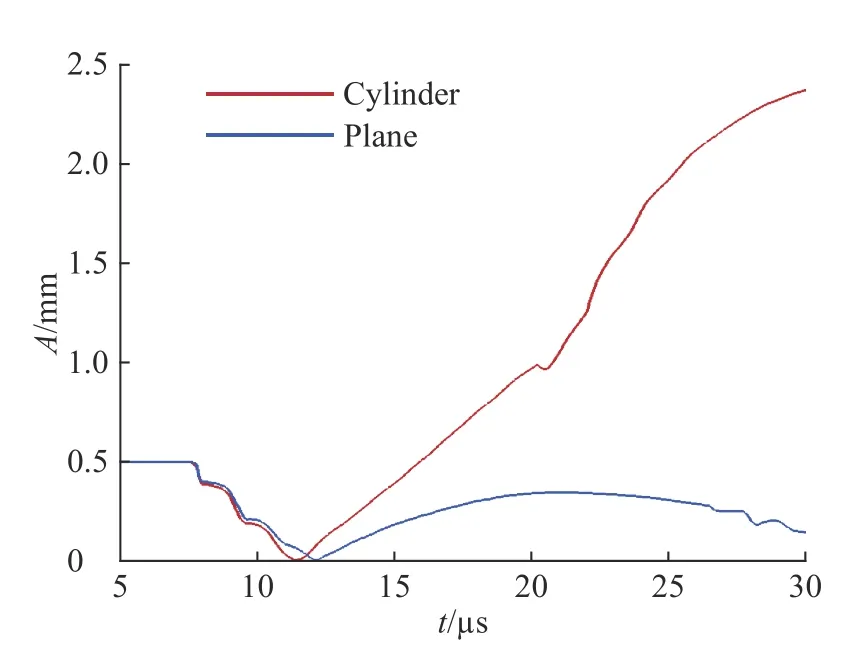
图 15 不同几何构型下的振幅增长曲线Fig. 15 Amplitude growth curves for different geometrical configuration

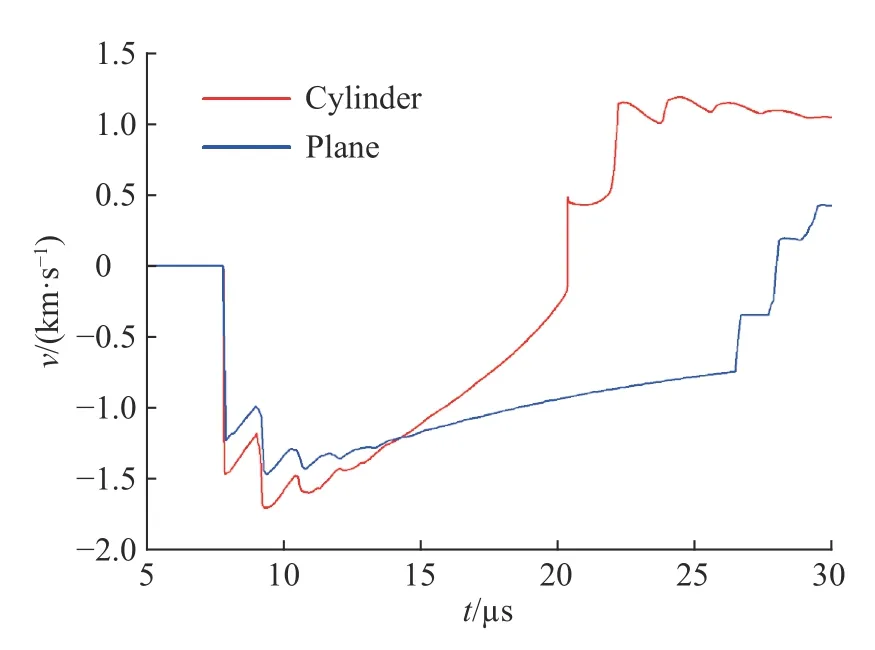
图 16 不同几何构型下的界面运动速度Fig. 16 Interface velocities for different geometrical configuration

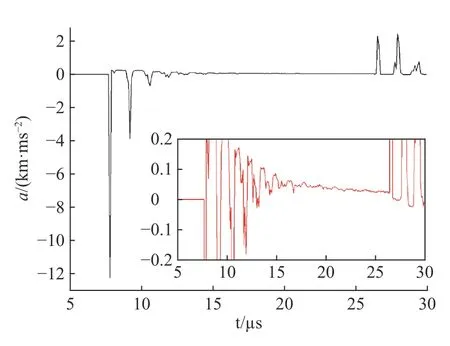
图 17 平面几何中的界面加速度Fig. 17 Accelerations of interface in planar geometry

3 结 论

基于欧拉有限体积法，发展了适用于多物质、大变形及强冲击波条件下流体弹塑性问题数值模拟的高保真度爆轰与冲击动力学计算程序。利用该数值模拟程序，研究了柱形汇聚几何中内爆驱动下金属材料界面不稳定性发展的动力学行为特征，得出以下结论。

（1）首次冲击后，钢壳开始聚心运动，在约12 µs 前，还受到了三次有效的向心反射压缩波加载，在此阶段，界面发展以RM 不稳定性为主；在12 µs 后到冲击波聚心反弹加载之前，界面聚心运动处于一种加速减速状态，界面发展由RT 不稳定性主导；在冲击波聚心反弹加载后，界面又受到四次有效的向心反射稀疏波加载，此时界面发展又由RM 不稳定性主导。

（2）初始扰动振幅较大，振幅增长较大；初始扰动模数较大，振幅增长较小，且存在一个截止模数（波长）；钢壳厚度会抑制扰动增长，也存在一个截止厚度；在相同初始条件下，相较于平面几何构型，汇聚几何结构中由于几何收缩效应和界面减速阶段较强的RT 不稳定性，使扰动增长速度更快。

金属材料和流体最大的区别在于金属材料的强度效应，而强度对扰动发展具有抑制作用。另外，由此带来的材料断裂破坏对扰动增长甚至混合都会产生影响，而且材料的断裂破坏机制也复杂多变，其他如金属材料的相变、微观结构特征等，都会影响金属材料界面不稳定性的发展，这都使金属材料界面不稳定性问题更加复杂。下一步，我们拟研究材料强度对金属材料界面不稳定性发展演化的影响，包括硬化、软化等机制。