空孔与运动裂纹相互作用的动焦散线实验研究*

杨仁树，肖成龙，丁晨曦，陈 程，赵 勇，郑昌达

（1. 中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室，北京 100083；2. 北京科技大学土木与资源学院，北京 100083；3. 中国矿业大学(北京)力学与建筑工程学院，北京 100083）

在井巷施工与城市地下工程等实际工程中，岩体通常存在大量的裂隙、孔洞等缺陷，当含缺陷的围岩受到工程活动等动载的影响，其内部缺陷附近产生应力集中现象，以致周围应力场发生改变，严重时会影响围岩的完整性，甚至造成岩体力学性质的削弱，最终导致围岩结构失稳。因此，对冲击荷载下含缺陷介质的动态断裂行为进行深入研究具有重要的工程意义。

近年来，对于在冲击荷载下介质的动态断裂破坏行为，国内外诸多专家学者进行了相关研究，取得了丰富的研究成果：Kalthoff 等[1]基于焦散线理论，测定了冲击荷载作用下裂纹尖端的动态断裂韧性；Rubinstein 等[2]研究了微观缺陷与裂纹的相互作用，分析了裂纹扩展过程中的动态断裂行为；姚学锋等[3]采用动态焦散线实验方法，设计冲击三点弯实验，研究了含偏置预裂纹有机玻璃(PMMA)试件的裂纹动态扩展行为；岳中文等[4]设计冲击三点弯实验，得到了不同倾角的层状岩体的动态断裂特征，裂纹的偏移距离随预制裂纹角度的增加而增大；李清等[5]对含不同倾角的预制裂纹的半圆盘试件受冲击荷载时的裂纹起裂时间、裂纹速度、断裂韧度等参数进行研究；杨仁树等[6]基于数字激光动态焦散系统，研究了含不同曲率缺陷的PMMA 试件受冲击荷载作用的时程与应力规律；杨立云等[7]设计双预制裂纹的三点弯实验，研究了在冲击荷载作用下次裂纹对主裂纹动态扩展行为的影响。以上研究成果丰富了冲击荷载下岩石的动态断裂理论，但在空孔与不同偏置距离裂纹的相互作用方面却鲜有研究。

本文采用动态焦散线实验系统，对不同预制裂纹偏移距离的含空孔PMMA 试件进行冲击三点弯实验，研究了预制裂纹不同偏移距离时运动裂纹与空孔的相互作用规律及试件的动态断裂特性；并通过MATLAB 程序计算试件裂纹轨迹的分形维数，从分形的角度分析不同偏移距离时空孔对裂纹轨迹的影响，以期为实际工程提供一定的理论支持。

1 动态焦散线实验

1.1 实验系统

实验系统为透射式数字激光焦散线系统[8]，如图1 所示，实验采用的高速相机型号为Fastcam-SA5(16G)，通过配备的PFV 软件可设置相机参数、采集数据，该相机最大拍摄频率可达1 000 000 s−1，本次实验拍摄频率设置为150 000 s−1（相邻照片间隔6.67 µs），焦散图片尺寸192×168 像素；实验光源为绿色光源激光器，该光源输出功率为0～200 mW，本次实验光源输出功率设定为50 mW。

图 1 数字激光动态焦散线实验系统Fig. 1 The system of digital laser dynamic caustics

1.2 实验原理及方法

实验采用动态焦散线方法[9]，该方法基于几何光学原理。实验时将试件置于两场镜间的平行光场，在落锤的冲击加载下，裂纹尖端应力集中，裂纹尖端附近的试件厚度发生改变，进而改变了材料的光学折射率，入射光通过试件后将偏离原传播方向，最终在参考平面上表现出界限分明的明暗区域，即焦散线与焦散斑[10-11]。

式中：deff为试件厚度，本次实验deff=5 mm；c 为材料的光学常数，本次实验c=0.85×10−10m2/N；z0为试件至参考平面距离，本次实验z0=0.9 m；F(v) 为动载作用下的修正系数，在具有实际意义的裂纹速度下，F(v)=1；g 为数值系数，g=3.17；Dmax为焦散斑的最大直径。本次实验中，deff、c、z0、F(v)、g 均为常数，因而通过对不同时刻的焦散图片中焦散斑最大直径的测量即可确定该时刻的裂纹尖端动态应力强度因子。

1.3 动焦散线实验设计

由于有机玻璃具有与岩石材料相似的动态断裂特性[14]，因而选用其作为本次模型实验的实验材料，该材料的动态力学参数如下[15]：膨胀波波速cp=2 320 m/s，剪切波波速cs=1 260 m/s，弹性模量Ed=6.1 GPa，泊松比µ=0.31，应力光学常数Ct=0.85×10−10m2/N。图2 为试件模型示意图，试件尺寸为220 mm×50 mm×5 mm（长×宽×厚），在试件几何中心通过激光切割预制半径R=3 mm 的空孔，试件底部垂直预制长10 mm 的裂纹。本次实验共5 组方案，5 组方案中预制裂纹偏移试件中心的距离L 分别为0、3、6、9、12 mm（0～4 倍空孔半径R），每组方案共3 组试件，共15 组，依次对应试件编号Sx−n(x=0，3，6，···，12，表示预制裂纹偏移距离为x mm；n=1，2，3，表示每种情况下的第n 组试件)。实验加载通过落锤自由下落冲击试件上表面的中心，即三点弯曲加载，本次实验的落锤质量为1 kg，落锤下落高度为300 mm，保证了每组实验中落锤对试件的冲击荷载一致，实验加载装置如图3 所示。

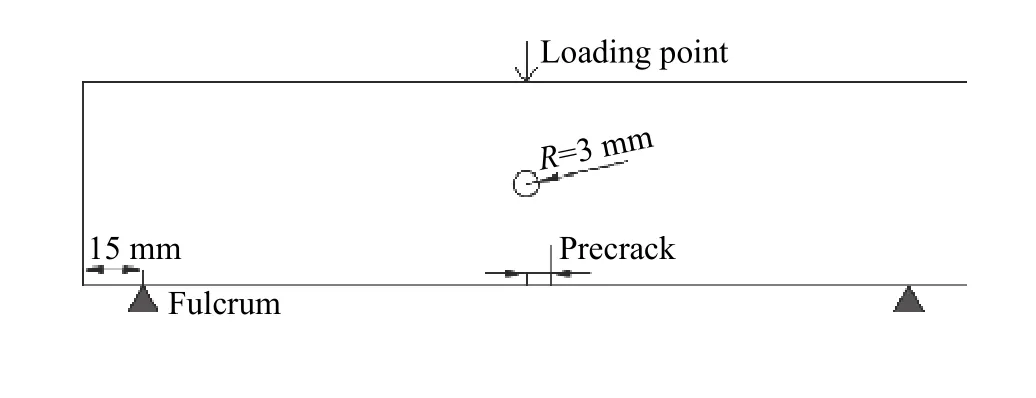
图 2 试件模型示意Fig. 2 Sketch map of the specimen

图 3 冲击加载装置Fig. 3 Impact loading system

2 动焦散线实验数据分析

2.1 试件断裂形态

5 组方案共15 组试件实验后，对各组实验数据处理分析，发现每组方案的各组试件实验结果基本一致，验证了本次实验结果的准确性与可靠性。图4 为每组方案中随机选取的一组试件S0-1～S12-1的裂纹扩展轨迹。由图4 可知，预制裂纹与空孔的相对位置对裂纹扩展轨迹产生显著影响，在冲击荷载的作用下，随着预制裂纹偏移试件中心距离由0 mm 增大至12 mm，试件共呈现三种破坏形态：当预制裂纹偏移距离不大于3 mm（试件S0-1、S3-1）时，裂纹起裂后贯穿空孔；预制裂纹的偏移距离增大至6 mm（试件S6-1），裂纹扩展至空孔附近时，空孔对运动裂纹呈现出显著的“吸引”作用，裂纹路径向空孔偏转，但未与空孔贯穿，随后裂纹远离空孔；预制裂纹偏移距离大于9 mm（试件S9-1、S12-1），裂纹起裂后即向落锤加载方向扩展，直至贯穿试件，空孔对裂纹的扩展轨迹无显著影响。

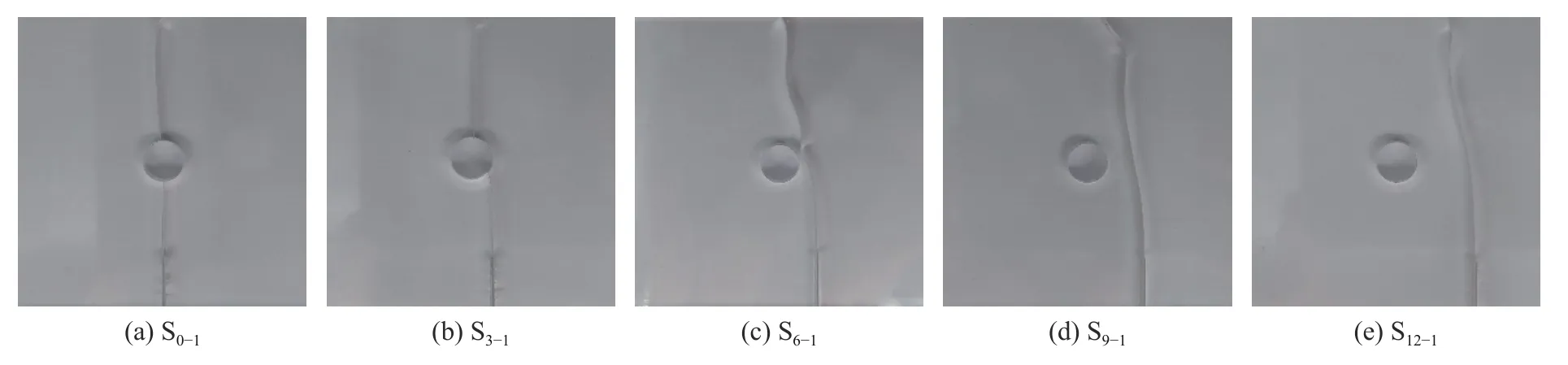
图 4 裂纹扩展轨迹Fig. 4 Crack propagation paths in different specimens

2.2 动态焦散斑图

由于篇幅所限，文中只给出试件S0-1、S6-1、S12-1各时刻裂纹与空孔作用的动态焦散斑图片，如图5 所示，记落锤与试件冲击接触的时刻为0 µs。

图 5 动态焦散斑系列图像Fig. 5 Dynamic caustic spots of specimens

试件S0-1裂纹尖端焦散斑的扩展可分为3 个阶段：第一阶段，落锤冲击试件时产生的应力波以加载点为圆心在试件传播，受应力波影响，预制裂纹尖端的焦散斑尺寸不断增大，即应力强度因子不断增大，在180.09 µs 时达到本次实验条件下的临界应力强度因子，试件起裂，226.78 µs 裂纹尖端焦散斑扩展至空孔下端；第二阶段，焦散斑融入空孔，空孔上方的阴影面积随时间不断增大，说明空孔上端发生能量积累，且能量的积累程度随时间加剧；第三阶段，当空孔上端能量累积到极值，600.30 µs 时空孔上端二次起裂，且焦散斑尺寸大于第一阶段，说明二次起裂所需能量大于一次起裂，起裂后裂纹向落锤加载处扩展，焦散斑尺寸减小，直至试件被裂纹贯穿。

试件S6-1裂纹尖端焦散斑的扩展可分为两阶段：第一阶段，在冲击荷载的作用下，预制裂纹尖端的焦散斑尺寸增大，试件于193.43 µs 起裂，起裂后裂纹快速扩展，并于246.79 µs 受空孔对运动裂纹的“吸引”作用显著向空孔偏转但未贯穿空孔，焦散斑尺寸逐渐减小；第二阶段，焦散斑于286.81 µs 开始远离空孔，并向落锤加载处不断扩展，焦散斑尺寸先增大后减小，直至贯穿试件。

试件S12-1在冲击荷载的作用下，预制裂纹尖端的焦散斑尺寸增大，试件于193.43 µs 时起裂，空孔对裂纹扩展未造成显著影响，裂纹向落锤加载方向不断扩展，直至试件被裂纹贯穿。

2.3 裂纹扩展速度

图6 为冲击荷载作用下5 组试件裂纹扩展速度与时间的关系曲线，由图可知，随着预制裂纹偏移试件中心距离由0 mm 增大至12 mm，裂纹扩展速度v 共呈现3 种变化规律。

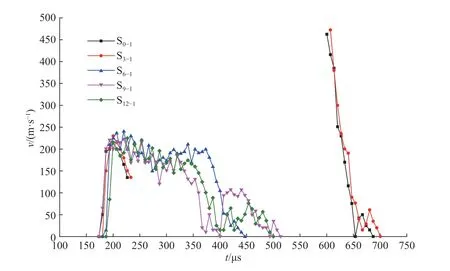
图 6 裂纹扩展速度随时间变化Fig. 6 Change of crack growth speed with time

试件S0-1、S3-1沿预制裂纹起裂后，裂纹速度迅速增大至214.89 m/s (200.10 µs)与229.88 m/s (200.10 µs)，随后速度减小，直至裂纹贯穿空孔。空孔上端能量积累，当能量累积到极值，空孔上端二次起裂，起裂速度分别达到462.48 m/s (600.30 µs)与472.42 m/s (606.97 µs)，该速度分别为一次起裂时速度峰值的2.15 倍与2.06 倍，说明二次起裂需要更多的能量，随后速度减小直至裂纹贯穿试件。

试件S6-1起裂后，裂纹速度迅速增大至240.7 m/s (226.78 µs)，随着裂纹靠近空孔，裂纹速度逐渐减小，并于280.14 µs 降低至谷值150.0 m/s，之后裂纹远离空孔，裂纹速度随之增大，由速度变化规律可知，空孔对裂纹扩展起显著抑制作用。最终裂纹速度不断减小直至裂纹贯穿试件。

试件S9-1、S12-1起裂后，裂纹速度迅速增大至222.66 m/s (220.11 µs)与224.89 m/s (226.78 µs)，随后速度振荡减小直至裂纹贯穿试件。由此可知，当预制裂纹偏移距离大于9 mm 时，空孔对裂纹速度的变化规律无显著影响。

2.4 动态应力强度因子规律

图7 为冲击荷载作用下5 组试件裂纹尖端动态应力强度因子与时间的关系曲线，由图可知，从落锤冲击接触试件到试件沿预制裂纹起裂的能量积累阶段(0～200.10 µs)，5 组试件动态应力强度因子随时间的变化规律基本一致，起裂时裂纹尖端基本相同，在0.93～1.00 MN/m3/2之间。起裂后裂纹尖端的能量释放，应力集中程度降低，随之减小，随着预制裂纹偏移试件中心距离由0 mm 增大至12 mm，试件起裂后共呈现三种变化规律。

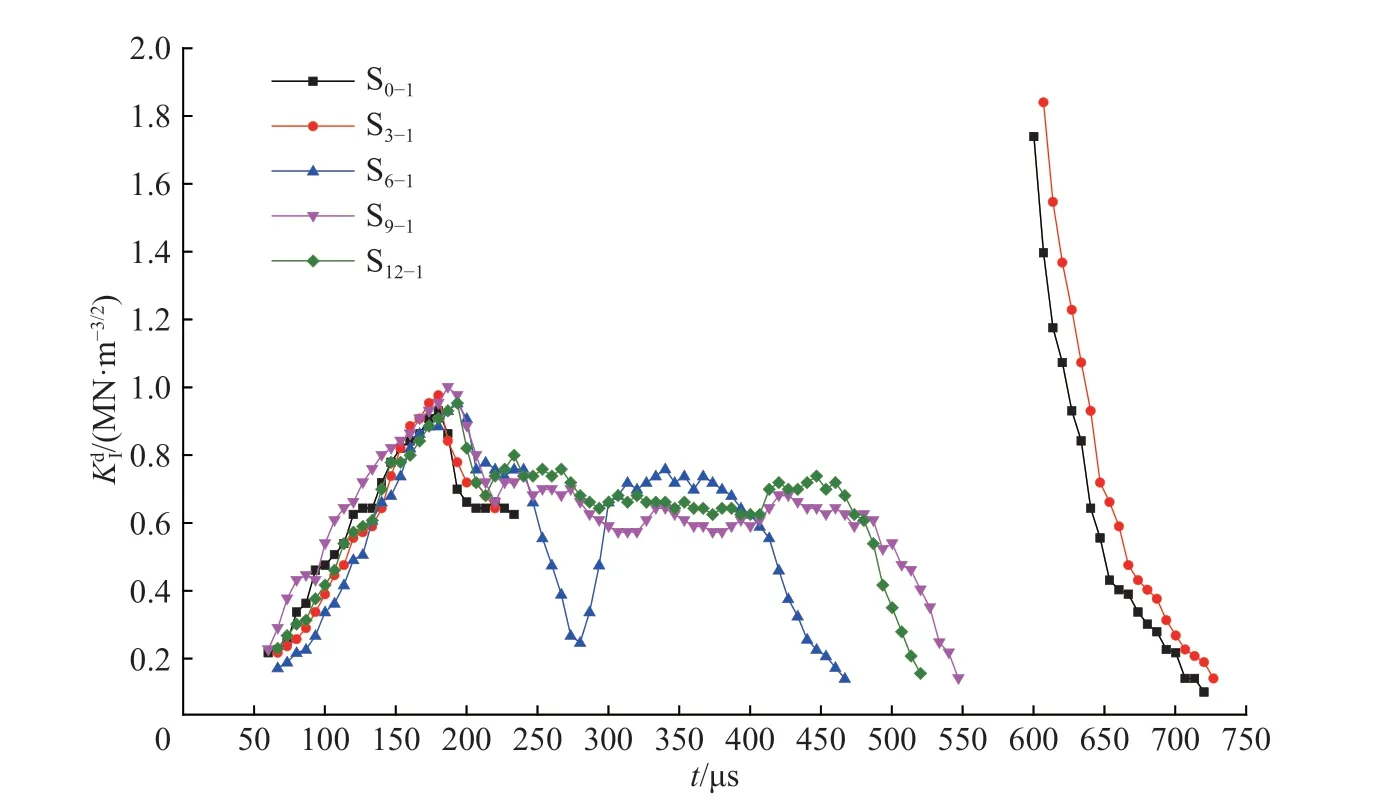
图 7 裂纹应力强度因子随时间的变化曲线Fig. 7 Change of crack stress intensity factor with time

(1) 试件S0-1、S3-1起裂后受空孔影响，分别减小至0.63 MN/m3/2(233.45 µs) 与0.64 MN/m3/2(220.11 µs)。裂纹贯穿空孔，空孔上端的能量不断积累，于空孔上端发生二次起裂，两组试件起裂时的分别为1.74 MN/m3/2(600.30 µs)与1.84 MN/m3/2(606.97 µs)，二次起裂的动态应力强度因子分别为一次起裂时峰值的2.76 倍与2.88 倍，说明二次起裂需要更多的能量，起裂难度更大。二次起裂后迅速减小直至裂纹贯穿试件。

(2) 试件S6-1起裂后受空孔的“吸引”作用，裂纹向空孔偏转，迅速减小，于273.47 µs 降低至谷值0.25 MN/m3/2，286.81 µs 裂纹开始远离空孔，随之增大，于333.50 µs 达到峰值0.76 MN/m3/2，由变化规律可知，空孔对裂纹扩展起显著的抑制作用。随后，逐渐减小直至裂纹贯穿试件。

(3) 试件S9-1、S12-1起裂后裂纹尖端能量释放，减小，并分别在0.57～0.74 MN/m3/2(220.11～426.88 µs)与0.63～0.80 MN/m3/2(213.44～446.89 µs)之间震荡，随后，逐渐减小直至试件贯穿。当预制裂纹偏移距离大于9 mm 时，空孔对裂纹尖端应力强度因子无显著影响。

3 裂纹轨迹的分形维数计算

分形理论由Mandelbrot 于1975 年创立，分形理论的出现为分析具有自相似性的不规则几何形体提供了定量刻画的方法[16]，且由谢和平[17]首次将该理论应用于岩石的损伤破环分析。其中，计盒维数由于其相对简单的计算方法，且能够准确表征裂纹空间分布[18-19]，因而在岩石断裂力学中得到了广泛应用。将分形体用边长为 δ 的盒子均匀覆盖，记 N (δ) 为所有与分形体相交的盒子个数，则计盒维数DB[20-22]的表达式为

图8 为5 组试件在冲击荷载作用下的裂纹轨迹进行二值化处理后的图片，图像尺寸为1 024×1 024像素，将二值图导入MATLAB 计盒维数计算程序进行计算。

图9 为5 组试件裂纹轨迹的计盒维数拟合直线，5 组拟合直线的相关系数均大于0.99，证明了试件在冲击荷载作用下的裂纹轨迹符合分形规律。试件S0-1～S12-1裂纹轨迹的分形维数D1～D5分别为1.222 0、1.308 8、1.319 2、1.292 1、1.279 0。当预制裂纹与试件中心无偏离时，裂纹轨迹的分形维数为五组试件中的最小值（1.222 0），说明该情况下裂纹轨迹复杂程度最低，裂纹的扩展轨迹最规则。当预制裂纹发生偏离时，裂纹轨迹的分形维数较试件S0-1增大，从分形的角度进一步验证了预制裂纹偏移距离与空孔对裂纹扩展的影响。预制裂纹与试件中心偏离6 mm 时，裂纹轨迹的分形维数为五组试件中的最大值（1.319 2），说明该情况下裂纹轨迹最复杂，裂纹的扩展轨迹规则程度最低。

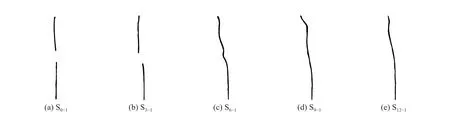
图 8 裂纹轨迹二值图Fig. 8 Binary diagrams of the crack trajectories in different specimens

图 9 裂纹轨迹的计盒维数拟合曲线Fig. 9 Box-counting dimension fitting curves of crack trajectories in different specimens

4 结 论

本次实验条件下，当预制裂纹偏移试件中心距离由0 mm 增大至12 mm（0～4 倍空孔半径R），存在2 个临界偏移距离6 mm (2R)、9 mm (3R)，在临界偏移距离裂纹的扩展轨迹、动态断裂特性发生显著变化，整体呈现为以下3 种规律：

（1）偏移距离不大于3 mm 时，裂纹贯穿空孔，空孔上端发生二次起裂，且二次起裂的速度与应力强度因子分别平均为一次起裂时峰值的2.1 倍与2.8 倍，二次起裂需要更多的能量，无偏移时裂纹轨迹的分形维数为最小值1.222 0。

（2）偏移距离由3 mm 增大至6 mm 时，裂纹不再贯穿空孔，裂纹扩展至空孔时首先向空孔偏转，随后裂纹远离空孔，空孔对裂纹先吸引后排斥，裂纹扩展速度与应力强度因子先减小后增大，裂纹轨迹的分形维数达到最大值1.319 2。

（3）偏移距离大于6 mm 时，空孔对裂纹的吸引作用逐渐减小；偏移距离大于9 mm 后，空孔对裂纹扩展无显著影响，裂纹起裂后即向落锤加载方向扩展，裂纹速度与应力强度因子振荡减小直至贯穿试件，裂纹轨迹的分形维数较6 mm 时有所减小。