设参建模 深度整合

胡嫚玲

各位评委大家好，我说我将从以下五个方面展开说题，一说题目，二说学情，三说教学，四说推广，五说价值。

1  说题目

如图1，△ABC是一块锐角三角形的材料，边BC=120mm，高AD=80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，正方形零件的边长是多少？

这道题出自于人教版九年级下册《相似三角形复习题》57页拓广探索第11题，本题涉及到的知识点有相似三角形的判定和性质，正方形的性质等。

该题目之所以出现在相似这一章的拓广探索复习题上，不仅是考察学生对本章所学能否应用于实践探索，更是对设参思想，建模思想的考察，也透露出数学与生活息息相关。

本题是设参，通过相似比例关系得到含有参数的方程，在解题时，通过以疑激趣，以疑启思，在精心设问下引发学生主动思考和探究，合理联想，突破解题思路，增强解题能力，提升数学思维，从而提高学生数学抽象、逻辑推理、数学建模、直观想象、数学运算等核心素养的发展。

2  说学情

学生对相似的性质和应用基本掌握，但在复杂情况下，对相似的模型识别能力欠缺，审题意识和能力不强，尤其对于隐含条件的挖掘比较欠缺，通过适时设参，转化为方程乃至函数，这种解决问题的经验缺乏，模型积累较少，因而造成学生对此题心生畏惧，容易回避。

3  说教学

受波利亚解题表中第一步弄清題意，第二步拟订计划，第三步实行计划，第四步回顾的启发，结合本题的实际背景，将本题的解题策略，分为以下5个环节1.思维铺垫，2.分析题目，3.关键点突破，4.解题过程，5.回顾梳理

3.1思维铺垫

首先以思维导图（图2）的形式来对本章的知识点进行回顾，在导图中，有意强调与本题相关联的点，为此题的解决做准备工作。

3.2分析题目

有研究显示，做一道题有70%的时间都应该在认真审题，所以此题的解题教学以问题驱动的方式帮助学生理解题意，进行审题分析;

3.3关键点突破

此题的关键点在于，一对应边的比等于对应高的比，二设参法，在学生由平行得到相似这一认知基础上，当学生分析到题中给的条件由底边BC，高AD，在图1中予以做标记，以此来提示学生，联想到对应底边的比等于对应高的比，在分析基本图形时，指出与正方形相等的边长KD恰好于大三角形的高AD重合，在对应边的比等于对应高的比的基础上，就可以用设参法列出关于边长的等量关系;

3.4解题过程

由学生到黑板上演示此题的解题过程，老师对其解题过程进行评价，以帮助其养成良好的解题习惯;

3.5回顾梳理

再由老师对本题的解题思路进行总结，为此题的变式做准备。

下面是我的教学实录

4  说推广

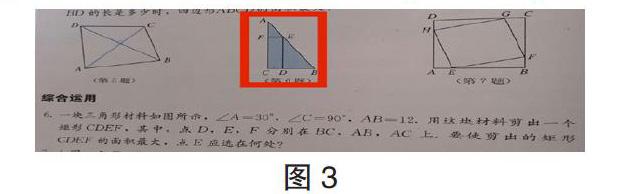
波利亚在《怎样解题中》指出：“变化问题使我们引进新的内容，从而产生新的接触，产生和我们问题有关的元素接触的新的可能性”，之所以选择这道题目，因为我发现在9上课本在实际问题与二次函数的复习巩固第六题习题中发现了类似的图形（图3）。

而这道题的考点是通过设参，建立二次函数模型，用二次函数性质来解决，从这里给了我灵感，大胆对第11题进行变式，新课标提出培养学生应用意识和模型思想，要求我们关注数学模型，从生活中来，到生活中去解决问题，我决定构设相似场景，把正方形变为矩形，解决在节约型社会下提倡物尽其用，如何截取才能使得矩形面积最大的问题。

变式1：如图4，△ABC是一块锐角三角形的材料，边BC=120mm，高AD=80mm，要把它加工成矩形零件，使矩形的一边在BC上，其余两个顶点分别在AB、AC上，如何裁剪，使矩形面积最大？最大面积是多少？

对变式1的教学流程

4.1自然过渡，将正方形变为矩形，如何截取，才能使得矩形面积最大？

4.2用动态图帮助学生分析题目，让学生在动态图的基础上理解面积变是由于长和宽在变，所以本题有三个变量;

4.3求面积最大值，要用二次函数，而二次函数是两个变量;

4.4本题的题眼就要借助上一题的思路利用相似模型在于找到长和宽的等量关系;

4.5三个变量减少为两个变量，就可以用二次函数模型来求最值。

设计意图：要想用二次函数解决矩形面积最大值，就要借助原题中的相似模型找到长和宽的等量关系，再用二次函数模型解决最值问题，在一道题中，对不同的数学模型，通过设参建模，进行整合，让学生在原有认知的基础上，对此题进行深度理解。

下面是我的教学实录

在变式1基础上，由特殊到一般，继续设参，底边a，高为h，类比变式1可得变式2的教学流程;

变式2：如图5，△ABC是一块锐角三角形的材料，边a，高h，要把它加工成矩形零件，使矩形的一边在BC上，其余两个顶点分别在AB、AC上，如何裁剪，使矩形面积最大？最大面积是多少？

1.将底和高换为字母;

2.类比上一题的解题思路即可求得题思路，师生共验证猜想。

设计意图：以变式1为原型，再次对一道题中不同数学模型通过设参进行深度整合，让学生体验攻坚克难的过程，树立其对数学的信心

下面是我的教学实录

5  说价值

义务教育数学课程标准（2011年版）旗帜性理念是培养学生的创新意识，提倡教学生学会思考，学会学习，通过原题的详细解决过程，变式1.2的适度延伸和探究，旨在让学生对问题有一个由浅入深的认识过程，在这个认识过程中对不同数学模型进行整合，让学生体会不同数学模型，在一道题目中存在时，能发现并提出新的问题，进而去分析和解决问题，这样的习题教学更是培养学生在遇到困难时攻坚困难，寻根问底，理性分析等良好数学品格的契机。

更重要的是能在不改变问题情境的状况下，自然过渡与切合，让学生意识到数学的“有用”，体会到解决问题帮助他人的愉悦感，为社会进步作出小贡献的成就感，会更增添学好数学，用好数学的决心。