论岩土施工企业生产效率预测与评估方法

廖辉辉

摘要：根据已知数据结构特点，进行回归分析形成线性的预测函数，对其显著性进行比较并进行优化处理，突破常规的用一次函数进行线性拟合的方法，最终建立起比线性预测函数精度更高的多元非线性关系的预测数学模型。对某岩土工程施工企业连续7个月在每个月的工程项目投入产出观测值与预测值进行比较，对其生产效率进行分析评估。这种分析方法也适用对其它领域的研究分析。

关键词：回归分析;拟合函数;显著;效率

Abstract： According to the known data structure characteristics， regression analysis is carried out to form a linear prediction function， and its significance is compared and optimized， which breaks through the conventional method of linear fitting with primary function， and finally establishes a prediction mathematical model of multi-element nonlinear relationship with higher accuracy than the linear prediction function. This paper compares the observed value and predicted value of the project input and output of a geotechnical engineering construction enterprise in each month for seven consecutive months， analyzes and evaluates its production efficiency. This method can also be applied to other fields.

Key words： regression analysis;fitting function;significance;efficiency

1  回归分析建立初步预测函数

1.1 已知数据结构特点

已知数据结构特点见表1。

1.2 回归分析

以Q为因变量，L和K为自变量进行回归分析，方差分析结果如表2、表3所示。

根据回归分析的结论得出回归方程即拟合函数：Q=-79.75+15.09×L+0.70×KF≥F1-α（m，n-m-1）时，回归效果显著，由方差分析有F=554.9319267>F0.95（2，4）=6.94，所以回归方程显著。

2  比较并优化预测函数

2.1 数据比较

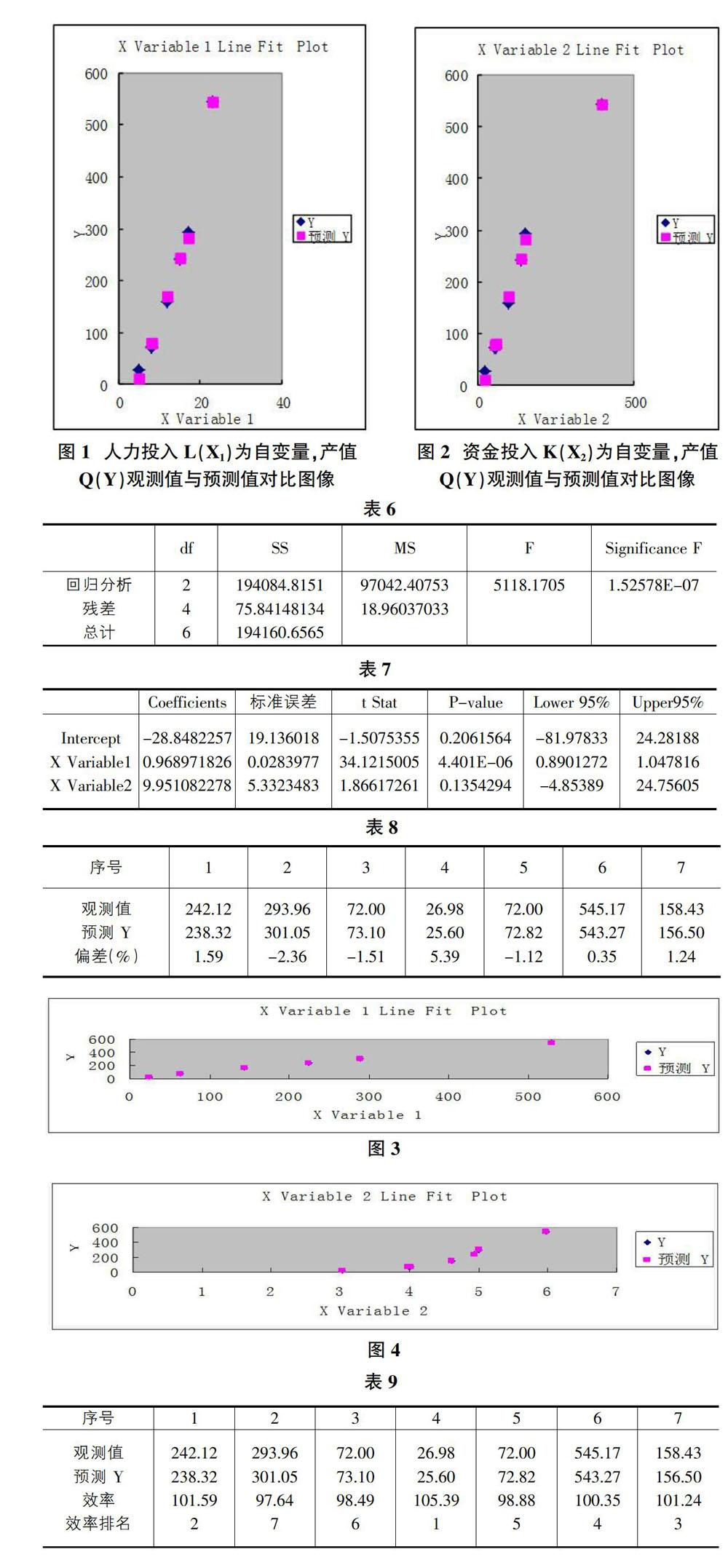
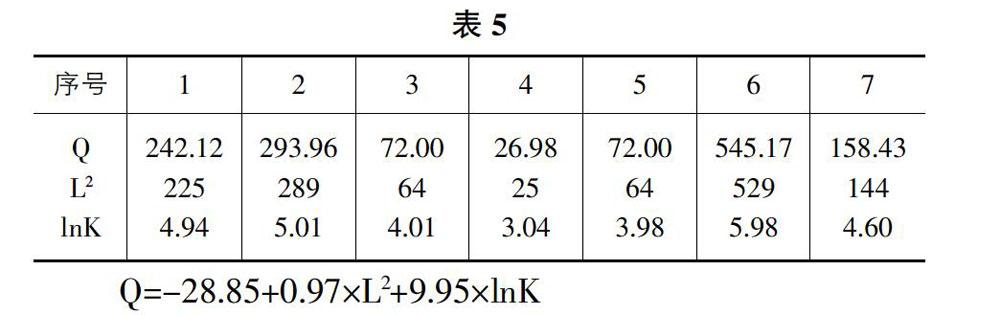
根据前面所求的拟合函数即回归方程Q=-79.75+15.09×L+0.70×K求出预测值与观测值的偏差率，数值及图像直观对比如表4、图1、图2所示。

2.2 数据优化

图可见，回归方程对总体的拟合效果显著，在序号为3、4、5、7项偏差较大，第4项偏差高达161.88%，可見拟合效果在局部范围存在较大缺陷，需进一步完善优化。

保持产值Q不变，对人力投入L和资金投入K进行数学转换，见表5。

以产值Q为因变量， L2和lnK为自变量进行回归分析，方差分析结果如表6、表7。

根据回归分析的结论得出回归方程即拟合函数：Q=-28.85+0.97×L2+9.95×lnKF≥F1-α（m，n-m-1）时，回归效果显著[1]，由方差分析有F=5118.1705>F0.95（2，4）=6.94，所以回归方程显著。

根据回归方程Q=-28.85+0.97×L2+9.95×lnK，求出预测值与观测值的偏差率，数值及图像直观对比如表8。

以L2（X1）为自变量时，产值Q（Y）的预测值与观测值对比图，图3。

以lnK（X2）为自变量时，产值Q（Y）的预测值与观测值对比图，图4。

从上方表格和图像明显可见预测值与实际值几乎重合，回归方程效果显著，最大偏差为第4项，相对偏差控制在5.39%以内，对总体及各点拟合均比前次所求回归方程显著。用Q=-28.85+0.97×L2+9.95×lnK进行预测效果更好，将此式作为投入产出预测函数。

特别指出，在进行优化处理时为何将多元一次线性回归方程即初次拟合的预测函数Q=-79.75+15.09×L+0.70×K转为含有幂函数和对数函数的多元非线性的预测函数关系式Q=-28.85+0.97×L2+9.95×lnK，以及如何在众多的函数关系中选定何种函数进行优化处理，需要另外进行专题讨论，本文中不做详细介绍。

3  分析评估

进行效率分析，效率=（观测值/预测值）*100%，结果如表9。

由此可知，某岩土工程施工企业7个月份中每个月生产效率均比较好，序号为4的月份最高。必须注意，这些效率值是根据该企业的预测函数计算得出，只是相对于预测值而言，效率值大于1者并不代表效率高于其他企业，也不代表没有改进的余地。随着生产力水平的提高，生产效率会不断提高，预测函数也会随之变化，原效率值会相对下降。

4  结语

此预测函数的实际意义是该企业在现有的技术水平条件下，如已知产值Q即签订的工程项目合同额，利用预测函数可预测资源投入情况，以便企业分析投入产出的效率。企业应不断挖掘提高效率的因素，提高其生产效率，促进企业向节能高效型发展。

参考文献：

[1]庄楚强，何春雄.应用数理统计基础[M].广州：华南理工大学出版社，2006.

[2]肖家祥，张健主编.三精管理[M].北京：中国建材集团有限公司企业管理部，2018.

[3]叶裕民.全国及各省市全要素生产率的计算和分析[J].经济学家，2002（3）.

[4]李小平，朱钟棣.中国工业行业全要素生产率的测算[J].管理世界，2005（4）.