环境标准样品均匀性检验数据漂移校正方法探讨
田衎, 贺岩涛, 张覃, 郭伟臣, 赵亚娴, 岳亚萍, 杨永
(生态环境部标准样品研究所, 国家环境保护污染物计量和标准样品研究重点实验室, 北京 100029)
环境标准样品作为环境监测量值传递与溯源的实物载体,主要用于环境监测过程中的质量控制和质量保证(QC/QA)、人员考核、分析方法验证、仪器校准等,是保证全国环境监测数据准确、可比的计量标准[1-3]。目前,随着国家对环境监测数据质量要求的提高,环境标准样品在环境监测领域的使用越来越受到重视[4-5]。均匀性是批量制备环境标准样品必须具备的基本属性之一,只有均匀性符合要求的标准样品,才能进行稳定性研究和协作定值[6]。对于土壤、沉积物等固体环境标准样品,均匀性不确定度分量更是其不确定度的主要来源之一[7-12]。因此,正确、合理地评价环境标准样品的均匀性及其不确定度对环境标准样品的研制具有重要意义。均匀性检验所用分析方法重点是保证具有不低于定值方法的精密度和足够的灵敏度(GB/T 15000.3—2008《标准样品工作导则》),但在实际均匀性分析测试过程中,在检验样品数量较大、样品基体较复杂等情况下,由于实验环境的变化或仪器性能本身的不稳定等,经常导致测量数据产生趋势性漂移,降低了标准样品均匀性判定结果的可靠性,甚至可能产生不合逻理的均匀性不确定度评定结果等,给环境标准样品的研制及使用带来不利影响。
影响分析数据漂移的因素较为复杂,相关校正方法报道不多,主要包括内标法、内插校正法等[13-16]。在标准样品均匀性检验过程中,为减少数据漂移的影响,一般推荐采用随机分析法(GB/T 15000.3—2008),该法不对漂移数据进行校正,仅通过随机分析的方法,使数据漂移对样品单元间和单元内的影响完全随机化,以达到减小数据漂移对标准样品均匀性评价的影响。国际标准化组织(ISO)最新发布的标准样品导则(ISO Guide 35:2017)推荐采用趋势分析校正法进行数据漂移校正,但主要以原则性描述为主,缺少技术环节的详细指导[17]。本文从实验方案和数理统计方法等方面,结合实例探讨了随机分析法、随机区组法、内插校正法、趋势分析校正法等方法应用于环境标准样品均匀性检验的技术细节,剖析了各方法的适用条件,以期为环境标准样品的均匀性评价提供借鉴。
1 实验部分
1.1 均匀性检验实验方案
对于批量制备的标准样品,依据样品总单元数和对标准样品均匀程度的了解,一般要求均匀性检验抽样的最小单元数在10~30之间,每个抽样单元应重复测量不少于2次(GB/T 15000.3—2008)。在均匀性检验分析结果存在趋势性漂移的情况下,可按照以下步骤进行均匀性检验:①采用随机分析法和随机区组分析等均匀性检验实验方案,这是目前均匀性检验样品分析常用方法,也是标准中推荐的方法;②在此基础上,如有必要,进行数据漂移趋势显著性判定,如果存在显著性漂移,采用内插校正法和趋势分析校正法等校正方法对数据漂移进行校正。
1.1.1随机分析法
将制备的均匀性检验样品编号后,按随机顺序进行分析测试。如30瓶均匀性检验样品,每瓶样品3个子样,按随机函数表将90个样品排序后进行分析测试。
1.1.2随机区组法
对抽取的多瓶均匀性检验样品,每瓶抽取一个子样分为1个区组,每次采用随机顺序完成1个区组样品的测试,通过多次独立分析完成全部区组样品的分析。
1.1.3内插校正法
在随机分析法的基础上,用漂移校正样品对数据漂移进行监控。漂移校正样品可以是实际样品,也可以是包含检验组分的其他样品。选定漂移校正样品测试频数后,先测试漂移校正样品,然后每测试几个样品(如5个、10个等)后重复测试漂移校正样品,为保证漂移校正结果的可靠性,漂移校正样品至少应平行分析2次以上。在整个测试过程中始终保持此频率对漂移校正样品进行分析测试。通过将漂移校正样品分析结果与其第1次分析结果进行t检验,或采用以下第1.1.4节趋势分析校正法中的直线模型等判定漂移趋势的显著性。如存在显著性漂移趋势,除第一个分析区间外,采用漂移校正样品的分析结果对每一个分析区间分别计算漂移校正系数,并对相应分析区间的结果进行校正,校正公式如下。
(1)
(2)
式中:y'i为校正后的数据,yi为分析测试的原始数据,Fk为第k个分析区间的漂移校正系数,Ck为漂移校正样品的第k个测试值。
1.1.4趋势分析校正法
将均匀性检验样品按随机分析法进行分析测试,检查数据是否有可观察的趋势,利用测试数据建立数学模型并对测试值进行校正。以最常见的线性漂移为例,即假定数据漂移量是时间的线性函数,测量值(y)与样品分析序号(分析时间,x)之间的线性方程为y=bx+a(式中a为直线的截距,b为直线的斜率)。用t检验法对直线斜率与零的差异进行显著性检验,直线斜率b的标准偏差(sb)计算公式如下:

(3)

(4)
tcal计算值为:
(5)
式中:se为剩余标准偏差,m为样品数量,其他各符号释义同上。在95%置信水平下,当tcal≤t0.95,n-2时,可认为检验组分的漂移是不显著的,可以忽略不计。当tcal﹥t0.95,n-2时,则认为检验组分的漂移是显著的,通过将原始测量值与漂移量进行叠加,实现测量值的漂移校正,校正的公式如下。
y'i=yi-b(x-1)
(6)
1.1.5均匀性检验评价方法
采用单因素方差分析法(ANOVA)评价标准样品均匀性的相关文献报道较多[18-21]。标准样品瓶间均匀性不确定度分量(ubb)的计算分为以下两种情况(GB/T 15000.3—2008)。
(1)当瓶间均方(MSb)远大于瓶内均方(MSw),则瓶间均匀性标准不确定度评定公式为:
(7)
(2)当均匀性检验分析方法的重复性欠佳时,则瓶间均匀性标准不确定度公式为:
(8)
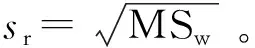
1.2 数据来源和分析方法
本文所用数据均为土壤中重金属元素标准样品均匀性检验数据。分析方法为电感耦合等离子体质谱法(ICP-MS)。
2 结果与讨论
2.1 随机分析法的适用条件及局限性
在均匀性检验样品数量较多、分析过程时间较长,或者样品基体较复杂等情况下,均匀性检验数据经常出现趋势性漂移,如果采用按单元间顺序依次重复测量,将会使数据漂移产生的系统误差更多统计在单元间测量方差中,使单因素方差分析法的统计量F值增大,这可能导致将本来均匀的标准样品判断为不均匀,产生误判,同时评定的瓶间均匀性不确定度分量也会偏大。为减小样品制备分装的趋势和数据漂移趋势可能存在的叠加效应,以及测量值趋势变化对均匀性检验统计分析结果的影响,普遍推荐采取随机分析法[22-24],从而使数据漂移对单元内方差和单元间方差的影响完全随机化,对统计量F和瓶间均匀性不确定度分量不致产生较大影响(GB/T 15000.3—2008)。这在趋势性漂移不显著的情况下适用,但在均匀性检验测试结果存在显著趋势性漂移的情况下,如果不对数据漂移进行必要的校正,由数据漂移产生的系统分析误差必将统计到单元内测量方差中,相当于降低了分析方法的精密度,这与均匀性检验必须选择不低于定值方法精密度的分析方法要求相悖。
均匀性是一个相对概念,与当前的分析测试水平紧密联系,由于数据漂移导致精密度不好的分析方法判断为均匀的样品,其实对于精密度良好的分析方法未必是均匀的,降低了均匀性结果判定的可靠性和严谨性。因此,在均匀性检验分析结果存在趋势性漂移的情况下,首先应采取措施降低漂移或者对分析结果进行必要的校正,否则会增加对标准样品均匀性产生误判的风险。
2.2 内插校正法和趋势分析校正法的示例及统计分析结果比较
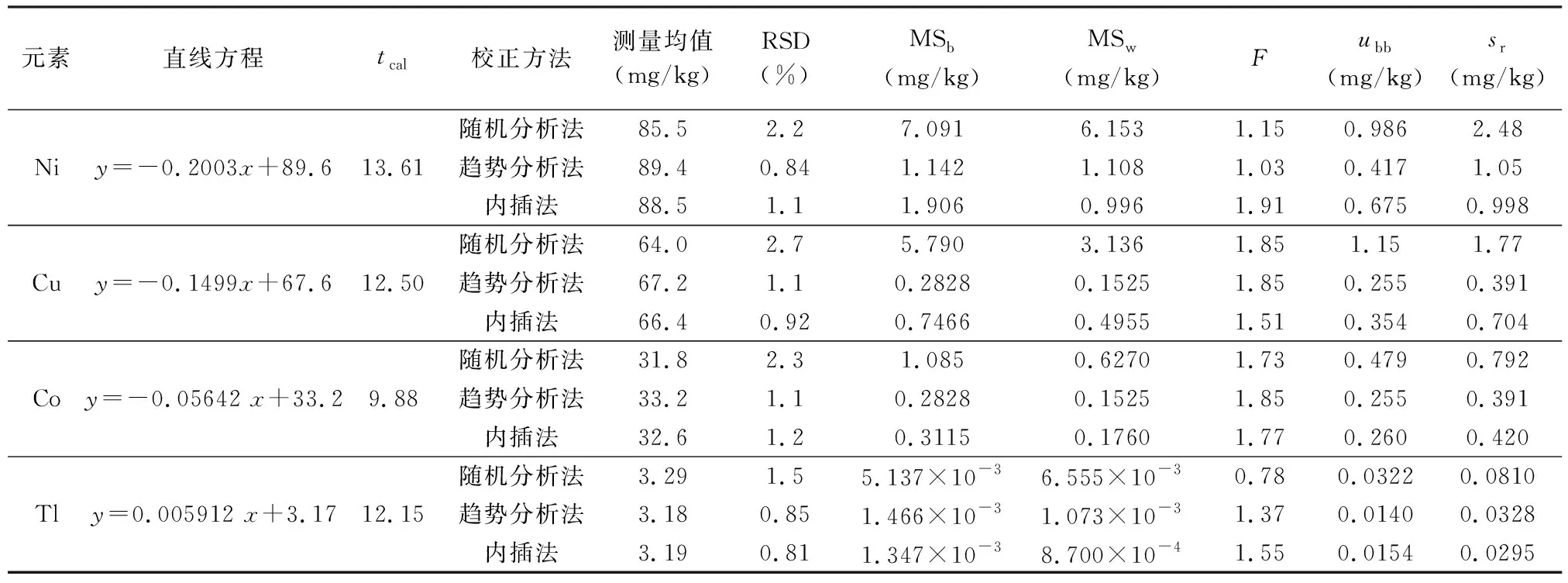
内插校正法应用于数据漂移的校正已有文献[13,25-26]报道,趋势分析法主要用于标准样品的稳定性研究[27-32],ISO发布的标准样品导则(ISO Guide 35:2017)推荐采用趋势分析校正法对均匀性检验中的数据漂移进行校正。表1为某土壤中Ni元素的均匀性检验分析结果,采用分层随机法抽取20瓶均匀性检验样品,每瓶样品平行分析测试2次,共计测试40次。由分析结果可见,随着测试时间的增加,测试值呈现逐渐降低的趋势,最后一个样品的测试值只有第一个样品的92%,测试值的相对标准偏差(RSD)高达3.0%。以分析序列号与测试值进行线性回归分析,回归方程为y=-0.2003x+89.6(y为土壤中Ni元素的测试值,x为分析序列号),回归方程斜率的标准偏差sb=0.01472mg/kg,tcal=0.2003/0.01472=13.6,tcal>t0.95,38(2.02),表明数据漂移是显著的。
分别采用内插校正法和趋势分析校正法对测试值进行校正,结果见表 1。校正前后均匀性检验分析结果的比较见图 1。由结果可见,测试值经采用内插校正法和趋势分析校正法校正后,RSD由3.0%分别下降为1.4%和1.2%,以分析序列号与校正后的测试值进行线性回归分析,并用t检验法检验斜率的显著性,结果表明直线的斜率与零无显著性差异,说明测量值的漂移趋势获得了很好的校正。
土壤中Ni、Cu、Co、Tl等4种重金属元素漂移校正前后均匀性检验数据分别采用单因素方差分析法进行统计分析,结果见表 2,其中趋势分析法和内插法均匀性评价结果均是在随机分析测试基础上的统计分析结果。由结果可见,在数据漂移趋势显著的情况下,采用内插校正法和趋势分析校正法,测量值的精密度和重复性标准偏差(sr)下降明显。与随机分析法相比,均匀性检验的4种重金属元素瓶间均匀性不确定分量均有不同程度的下降,最高下降幅度达78%。由此可见,数据漂移对标准样品均匀性不确定度的影响不容忽视,通过对数据漂移的校正,可有效避免对瓶间均匀性不确定度分量的不合理评定。
表1 土壤中Ni元素漂移校正前后均匀性检验分析结果
Table 1 Homogeneity data of Ni in soil before and after drift correction

分析序列样品编号①Ni含量(mg/kg)校正前内插法趋势分析法分析序列样品编号①Ni含量(mg/kg)校正前内插法趋势分析法监控样-1-26.4--监控样-4-25.30.9508②-112-287.587.587.5259-285.089.489.8214-188.388.388.52613-283.387.688.333-288.388.388.7274-184.889.290.047-187.887.888.4285-283.387.688.7516-188.388.389.12915-182.586.888.1620-288.088.089.0305-183.087.388.8711-188.888.890.0312-284.088.490.0819-188.388.389.73215-282.586.888.7监控样-2-26.00.9811②-监控样-5-24.90.9337②-920-189.090.790.6338-182.888.789.21019-286.888.588.63413-182.087.888.6119-189.090.791.0354-281.086.887.81217-188.590.290.73618-181.887.688.81314-288.089.790.43711-284.090.091.2148-288.390.090.9387-283.389.290.71517-287.589.290.3393-182.888.790.41618-288.089.791.04016-280.886.588.6监控样-3-25.80.9678②-监控样-6-24.4--172-185.588.388.71810-186.589.489.91912-186.088.989.62010-287.089.990.8216-287.089.991.0226-184.587.388.7231-183.586.387.9241-283.886.688.4
注:①样品编号规则为:横线前面数字为瓶号,横线后面为子样编号。如12-2,其中12为第12瓶样品,2为第12瓶第2个子样;
②为漂移校正系数。
表2 土壤中4种重金属元素漂移校正前后均匀性检验分析结果比较
Table 2 Comparison of homogeneity data of four heave metals in soil before and after drift correction
元素直线方程tcal校正方法测量均值(mg/kg)RSD(%)MSb(mg/kg)MSw(mg/kg)Fubb(mg/kg)sr(mg/kg)随机分析法85.52.27.0916.1531.150.9862.48Niy=-0.2003x+89.613.61趋势分析法89.40.841.1421.1081.030.4171.05内插法88.51.11.9060.9961.910.6750.998随机分析法64.02.75.7903.1361.851.151.77Cuy=-0.1499x+67.612.50趋势分析法67.21.10.28280.15251.850.2550.391内插法66.40.920.74660.49551.510.3540.704随机分析法31.82.31.0850.62701.730.4790.792Coy=-0.05642 x+33.29.88趋势分析法33.21.10.28280.15251.850.2550.391内插法32.61.20.31150.17601.770.2600.420随机分析法3.291.55.137×10-36.555×10-30.780.03220.0810Tly=0.005912 x+3.1712.15趋势分析法3.180.851.466×10-31.073×10-31.370.01400.0328内插法3.190.811.347×10-38.700×10-41.550.01540.0295

图1 土壤中Ni元素漂移校正前后均匀性检验分析结果比较Fig.1 Comparison of homogeneity data of Ni in soil before and after drift correction
2.3 内插校正法和趋势分析校正法的优缺点比较
内插校正法为每一个分析区间分别计算漂移校正系数,校正模型简单,校正准确度高,适用范围也比趋势分析校正法广泛。为进一步提高校正的准确度,可假设每一个分析区间数据漂移均呈线性变化,根据内插法的校正原理,可为每一个样品分别计算一个漂移校正系数,这与数据实际漂移过程是连续变化的过程更为相符。内插校正法的主要缺点是校正系数取决于分析区间前后两个漂移校正样品分析的准确度,因此对漂移校正样品的分析准确度要求较高。此外,在测量过程中需要插入漂移校正样品,无疑会增加分析测试的工作量。
趋势分析校正法充分利用了全部分析数据,校正系数稳健性较内插校正法好。趋势分析校正法的校正效果与拟合曲线的质量直接相关,虽然大部分数据漂移类似于线性,但影响数据漂移的原因复杂,多种因素共同作用的结果可能使数据漂移在一些情况下是非线性的,建立适合的漂移数据校正数学模型相对比较困难,导致趋势分析校正法适用范围没有内插校正法广泛。
2.4 随机区组法
随机区组设计在各种实验研究中被广泛应用[33-35],但我国应用随机区组法进行标准样品的均匀性检验鲜见报道。均匀性检验抽样的最小单元数在10~30之间,按每单元平行分析2~3次计,样品测试数量在20~90之间。在样品前处理复杂冗长,或者测试值漂移校正效果欠佳等情况下,一次不能完成全部样品的分析测试,可采取随机区组法均匀性检验方案,即通过将均匀性检验样品分为多个区组,每次采用随机顺序仅完成一个区组样品的分析测试,通过多次独立分析完成全部区组样品的分析。由于不是一次完成全部样品的分析测试,测试值受样品均匀性和分析方法再现性两个因素影响,因此均匀性检验分析结果宜采用双因素无重复方差分析法评价。
以土壤中Pb元素均匀性检验为例,分层随机抽取20瓶均匀性检验样品,每瓶样品分析测试3次,共测试60次。将样品分为3个区组,每次完成1个区组样品的分析测试,分析结果见表 3。
表3 随机区组法分析土壤中Pb元素分析结果
Table 3 Analytical results of Pb in soil using a randomized block design method

序号Pb平行测定结果(mg/kg)第1次测试第2次测试第3次测试测定平均值(mg/kg)120.520.419.220.0221.220.119.420.2320.420.319.720.1420.220.719.320.1520.220.319.119.9621.319.719.520.2720.719.119.219.7820.319.619.419.8919.819.419.219.51021.220.319.520.31119.920.419.419.91220.019.619.519.71319.619.219.519.41419.519.419.719.51520.719.619.519.91619.819.619.319.61721.220.019.420.21820.319.319.619.71920.419.219.619.72019.819.119.219.4均值20.419.819.419.8
为评价随机区组法评价结果的可靠性,本研究后续将开展随机区组法与随机分析法的比对工作。
表4 土壤中Pb元素的双因素无重复方差分析法统计分析结果
Table 4 Statistical results of Pb in soil by two-factor non-repetitive analysis of variance

变异来源离均差平方和(SS)自由度均方(MS)FPFcrit瓶间4.793190.25221.470.15311.87区组间9.01224.506126.266.89×10-83.24瓶内6.521380.1716---总计20.32659----
3 结论
本研究针对环境标准样品均匀性检验过程中测量数据产生趋势性漂移的问题,详细讨论了随机分析法、随机区组法、内插校正法、趋势分析校正法等方法在环境标准样品均匀性检验中的应用。结果表明:如果漂移趋势不显著,采用随机分析法有利于标准样品均匀性及不确定度的评价。在数据漂移显著的情况下,必须对测试数据进行校正。采用趋势分析校正法和内插校正法均可取得良好的校正结果。但在使用这两种校正方法时需要判断其校正能力,尤其是趋势分析校正法要判断漂移校正数学模型的合理性。在一次不能完成全部样品分析测试,或者在长时间分析测试过程中数据漂移校正效果欠佳的情况下,推荐采用随机区组法进行均匀性检验。
均匀性检验是标准样品研制中技术性较强、难度较大的环节。均匀性检验过程中产生数据漂移的原因复杂,且校正方法种类有限,对标准样品均匀性及其不确定度评价等相关工作还需深入开展研究。同时,需加快推进对最新ISO国际指南和标准的中文转换,以规范和指导我国环境标准样品研制工作。

