非稳态环境下行为调节对人体火用平衡的影响

范可新 王友群 张爽 刘升男

1 西安建筑科技大学建筑设备科学与工程学院

2 西部绿色建筑国家重点实验室（西安建筑科技大学）

0 引言

目前主要有平均预测投票（PMV），自适应模型和火用分析等3 种方法被用于研究室内人体的热舒适状况[1]。PMV-PPD 指标法是Fanger 在实验条件下建立人体能量平衡方程、并结合调查问卷分析而提出的，它建立起了室内热环境参数与人体热舒适感之间的关系，但并未考虑人体自身的行为调节。自适应模型是基于在自由运行建筑中的实测和调查问卷得出的，表明人体热舒适感与室外月平均温度密切相关，却不能反映室内环境参数的影响。火用分析方法综合了热力学第一和第二定律来对人体能量传递过程中不可逆因素所引起的损失进行分析，同时兼顾了室内、外环境参数的影响，可用于自然通风以及空调建筑的热环境评价。

目前，不少学者[2-6]提出了人体火用平衡模型用于人体热舒适状况，然而大多数是应用于稳态条件下。2011 年Shukuya 等[7]探究夏季动态环境下人体火用损失速率的变化规律，研究发现人员从室外环境进入空调房间时，人体火用损失速率突然减小。2012 年Shukuya等[8]探究冬季动态环境下人体火用损失速率的变化规律，研究发现人员从室外环境进入供暖房间时，人体火用损失速率突然增大。2016 年Shukuya 等[9]分析了冬季人体火用平衡与行为适应性的关系，结果表明适应性行为可以降低人体火用损失速率。

行为适应是指人们通过物理调节的手段来改变热交换条件以适应环境，如改变衣着、活动量等[10]。目前。火用分析方法在动态环境下的应用很少，主要的研究方法是给定一个人的活动水平和服装热阻，通过测量室内外环境参数数据，计算出人体火用损失速率，探究动态环境下人体火用损失速率的变化规律以及人体火用损失速率与热舒适评价指标的关系。然而目前人体火用分析方法在非稳态环境下的评价应用很少，主要研究关注于动态环境下，环境参数对人体火用损失速率的影响规律以及人体火用损失速率与主观热感觉评价的关系。且用人体火用分析方法与行为适应性关系的研究尚不充分。

因此，本文旨在已有的稳态模型[6]的基础上，考虑人体的火用蓄存速率，并引入风速对服装热阻和蒸发热阻的修正方程，提出新的一种新的非稳态人体火用模型，接着将模型计算得到的皮肤温度与已有的实验中皮肤温度测量值进行比较，以表明本文模型对预测皮肤温度的准确性，同时将模型计算得到的人体火用损失速率与已有的动态模型计算结果进行比较，以表明本文动态模型的合理性。最后用本文所建的动态模型探究非稳态环境下人体火用速率与行为适应性的关系。

1 非稳态人体火用模型

1.1 模型的建立

火用分析结合了热力学第一和第二定律，可以对人体与环境之间能量交换过程中的不可逆性强弱进行分析。人体作为开口热力系统，由正常状态可逆转变到与周围环境平衡所做的最大有用功可以用人体火用表示，但实际过程并非可逆，因此就存在人体火用损失速率。人体与环境之间换热过程的火用流图如图1 所示。

图1 非稳态人体火用流图

稳态条件下，王永杰等[6]厘清了新陈代谢热火用和湿火用，提出更合理的人体新陈代谢火用计算方法，建立了一种新的稳态模型，在模型中视火用蓄存速率为零。然而由于人体多数处于动态环境时，或者有时人员进行一些行为调整，使得人体的蓄热量是变化的，此时应该考虑火用蓄存速率项。本文在稳态模型的基础上，考虑到火用蓄存速率，进而建立一种非稳态人体火用模型。火用方程如下式所示。

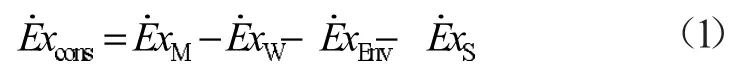
1.1.1 代谢火用速率

新陈代谢火用分为三部分：新陈代谢热火用，核心层湿代谢产生的湿代谢火用，皮肤层湿代谢产生的湿代谢火用。计算公式如下。

1.1.2 呼吸火用速率

人体核心层和周围环境直接通过呼吸的方式进行热交换，呼吸换热对应的火用率为呼出与吸入气体的火用值差。呼吸火用速率可由下式确定：

1.1.3 对流火用速率

对流换热产生的对流火用可通过下式确定

式中：hc,cl为人体着装表面对流换热系数，W/(m2·K)；Tcl和Ta分别为服装温度和空气温度，K。

1.1.4 辐射火用速率

辐射换热产生的辐射火用可通过下式确定

式中：feff为服装有效系数；ε 为发射率，取0.95；σ 为Stefan-Boltzmann 常数；Tr则为室内空气平均辐射温度，K。

1.5 蒸发火用速率

蒸发换热对应的蒸发火用可通过下式计算：

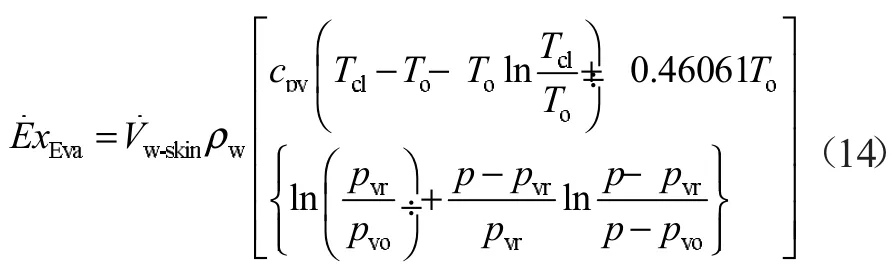
1.6 火用蓄存速率

人体火用蓄存速率等于皮肤层火用蓄存速率与核心层火用蓄存速率之和，即：

此外，由于外部风速以及身体运动又会使服装热阻以及蒸发热阻减小。因此，本文在建模时引入了ISO9920[12]中风速对服装热阻及服装蒸发热阻修正方程。当风速大于0.15 m/s 时，修正方程如下。

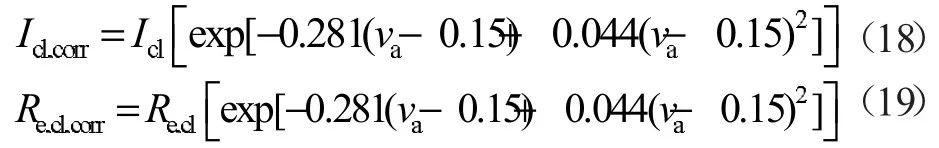
式中：Icl,corr为风速修正后的服装热阻clo；va为风速，m/s；Re,d,corr为风速修正后的服装蒸发热阻，m2·kPa/W。

从上述公式可以看出，人体火用损失速率不仅与环境参数有关，还与人体生理参数有关。将这些参数代入Gagge 的两节点人体热平衡模型中，通过MATLAB计算出人体皮肤温度，核心温度以及服装温度等，然后将这些人体温度带入火用平衡方程中，计算得到人体火用损失速率。

1.2 非稳态人体火用模型的验证

1.2.1 两种模型皮肤温度的比较

为了验证本文模型预测皮肤温度和核心温度的准确性，将计算出的皮肤温度和核心温度与Kakitsuba等[13]实验测得的数据进行比较。实验时，受试人员着棉衬衣和短裤，服装热阻约为0.5 clo，在温度为28 ℃，相对湿度为50%的房间停留30 min，然后进入温度为40 ℃，相对湿度为50%的房间停留60 min。图2 对比给出受试者暴露在40 ℃环境时的核心温度（直肠温度）及平均皮肤温度测量值以及本文模型的核心温度及皮肤温度计算值。结果表明本文模型对皮肤、核心温度的预测值与测量值吻合较好。皮肤温度之间最大的差异为0.26 ℃，核心温度之间最大差异为0.31 ℃。

图2 预测值与Kakitsuba[13]实验测量值的比较

1.2.2 两种模型人体火用损失速率的比较

为了进一步验证本文所建立的非稳态人体火用模型在动态条件下应用的正确性，将本文模型的火用损失速率计算值与Shukuya 等[9]中的两个case 的计算结果进行了比较。每个case 假设人员在室外活动1 h 后进入室内停留3 h。室外的计算的条件为：室外空气温度为5 ℃，代谢率为1.5 met，衣服热阻为2 clo。室内外相对湿度均为40%，室内外风速均为0.1 m/s。室内的计算条件为：case1 和case2 室内空气温度均为10 ℃，室内空气温度等于平均辐射服温度，case1 在室内期间的衣服热阻为0.9clo，case2 在室内期间的衣服热阻为2clo。相比之下，case1 和case2 相当于人员从室外进入一个正供暖的室内，而case1 相比case2，case1 相当于人员进入室内后脱掉了衣服。如图3 所示。

如图3 所示，通过本文所建立的非稳态火用模型计算出人员在室外期间人体火用损失速率值比Shukuya 模型的计算值小。这是由于Shukuya 模型中视新陈代谢的能量为新陈代谢热来计算热代谢火用，但其中包含了湿代谢的能量，因此所得新陈代谢火用比本文模型的计算结果大。两个模型的最大差异达到1 W/m2。本文非稳态火用模型计算出人员在室内期间的人体火用损失损率值比Shukuya 模型的计算值大。这主要是在室外期间由于本文计算代谢热火用时减去了湿代谢的能量，使得皮肤温度要比Shukuya 的低。为维持体温，身体开始颤抖，且比Shukuya 的要强烈，进入室内皮肤温度和核心温度要比Shukuya 计算的高，使得皮肤表面与室外之间的温差增大。

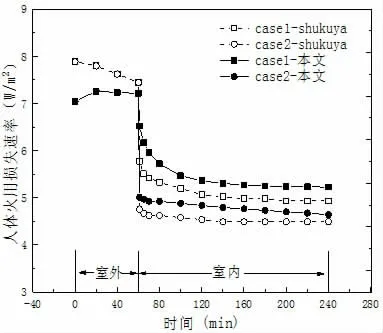
图3 突变条件下本文模型的人体火用损失速率与Shukuya[9]中数据的比较

综上，通过建立的非稳态火用模型与Shukuya 模型在突变条件下所计算出的人体火用损失速率的比较，在突变条件下，本文所建的非稳态火用模型与Shukuya 模型计算出的人体火用损失速率变化趋势一致，均在进入室内短暂时间内瞬间下降，并逐渐趋于稳定值。

2 模型计算结果与讨论

生活中，人们所处的环境大多数是动态的，有时人们为了达到舒适可能有时会进行一些行为调整，如脱衣服，启停空调，开关风扇等。因此，为探究夏季人员由室外进入室内的进行行为调整的过程中人体火用损失速率的变化规律。假定人员在室外行走30 min 后进去室内静坐办公60 min。在此期间空气温度等于平均辐射温度。固定条件如表1 所示。表2 为四个比较情况，是生活中常见的行为调整。case1 相当于人员进入室内后打开风扇，case2 相当于脱掉衣服，case3 相当于打开风扇并脱去外套，case4 相当于人员开启空调。

表1 固定条件

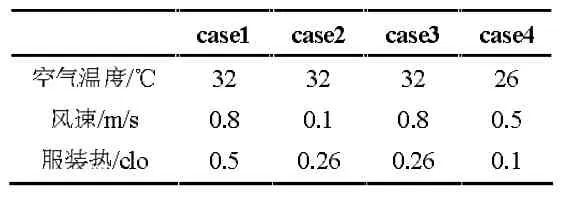
表2 比较条件

2.1 非稳态环境下的生理参数

图4 为生理参数如皮肤温度，核心温度，出汗量，皮肤层血流量随时间的变化曲线。

图4 生理参数

如图4 所示，当人员从室外走进室内时，四种情况的生理参数均随着时间推移而降低并趋于稳定。且case3 和case4 的生理参数减小幅度比case1 和case2的要大。图4（a）～（b）中显示，在室内期间，皮肤温度和核心温度的下降顺序是相同的，具体分别为case2＞case1＞case3=case4。图4（c）～（d）显示，在室内期间，出汗量和皮肤层血流量的下降顺序是相同的，分别为case2＞case1＞case3＞case4，且case4 的下降幅度明显比其他三种case 的要大。图4（e）显示，服装温度的下降顺序分别为case3＞case2＞case1＞case4。

2.2 非稳态环境下的火用速率

图5 为各项火用速率如代谢火用速率，火用交换速率，火用蓄存速率，火用损失速率随时间的变化曲线。

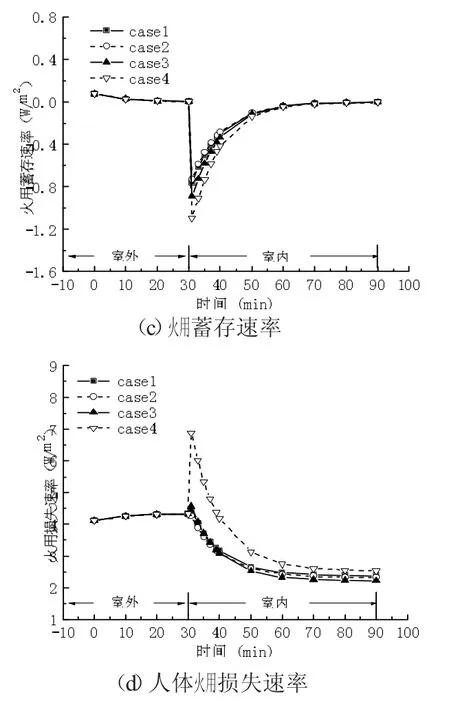
图5 人体火用速率

如图5 所示，当人员从室外走进室内后，四种case 的生理参数随着时间的变化呈不同的变化规律。且case4 的各项火用速率的下降幅度明显比其他三种的要大。这是由于case4 的生理参数的下降幅度较大，如图4 所示。

图5（a）显示，在室内期间，由于代谢率的突然降低，case1～case3 的代谢火用速率均随着时间以相同的下降速率逐渐下降并趋于几乎相同的稳定值。而case4却先急剧增大，然后逐渐减小并趋于稳定值。这说明代谢火用速率发生了“超越”现象。这主要是由于温度的突然降低，人体生理调节受到破坏，使得皮肤和核心层与室外之间的温差突然增大，但随着时间的推移，生理调节开始起作用，使得代谢火用速率趋于稳定状态，如图4 所示。

图5（b）显示，在室内期间，火用交换速率的下降顺序为case3＞case2＞case1＞case4。因为火用交换速率是对流火用速率，辐射火用速率，蒸发火用速率之和，受服装与空气温度和辐射温差以及汗液量的影响。虽然case3 的汗液量比case2 的要小，但case3 的服装温度与空气温度和辐射温度之间的温差比case2 的要大。

图5（c）显示，当人员从室外进入室内时，人体火用蓄存速率急剧下降，变为负值。逐渐升高趋于0。这说明人体火用蓄存速率也发生了“超越”现象，且在进入室内后的前几分钟内，人体火用蓄存速率的“超越”现象尤为明显。从图5（c）看出，case 4 的变化幅度比其他三种case 的要大。此外，case4 的火用蓄存速率再次达到稳定值所需的时间也最长，为50 min，其他case 所需的时间均为40 min。这是由于复杂的生理调节如出汗量与皮肤层血流量的减小共同作用引起的，如图4（c）～（d）所示。

图5（d）显示，当人员从室外进入室内后，四种case 的人体火用损失速率先增大，然后逐渐减小并趋于稳定值。这说明人体火用损失速率也发生了“超越”现象。从图5（c）看出，case4 的火用损失速率的“超越”现象尤为明显，变化幅度也是最大的，再次达到稳定值所需的时间也是最长的，为50 min，其他case 所需的时间均为40 min。此外，case4 的人体火用损失速率再次达到稳定值也是最大的，其次为case2 和case1，但case2 和case1 的作用相当，两种case 的人体火用损失速率非常接近。case3 的人体火用损失速率值最小，这与火用交换速率的降低顺序正好相反，如图5（b）所示。

综上所述，在夏季，人员的一些行为调整使人体火用损失速率出现“超越”现象，case3 即人员打开风扇并脱去衣服这种行为调整虽然出现了人体火用损失的“超越”现象，但没有人员开启空调情况下那么明显，且再次达到稳定的值也比其他三种情况要小。这样还可以减少空调运行时间，有利于节能。

3 结论

本文考虑到人体热蓄存率以及风速对服装热阻和蒸发热阻的修正，而建立了非稳态人体火用模型，探究了夏季人员一些行为适应下人体火用损失速率随时间的变化规律，本文的主要研究结论如下：

1）本文建立的非稳态人体火用模型对人体核心及皮肤温度的计算值与实验测量值有很好的吻合度。

2）在夏季时，人员的一些适应性行为使人体火用损失速率发生“超越”现象，尤其在开启空调情况下尤为明显。

3）从火用分析角度研究夏季人员的四种适应性行为，脱去衣服和打开风扇的作用是相当，此外，进入室内后开启空调情况下人体火用损失速率再次达到的稳定值最大，打开风扇并脱去衣服情况下最小。