排风隔热墙的二维频域模型研究

李辽 王劲柏 张冲 杜前洲 蒋诗宁

华中科技大学建筑环境与能源应用工程系

0 引言

排风隔热墙[1-2]属于新型的围护结构，其基本结构图如图1 所示。从室内侧到室外侧分别是多孔层，空腔层以及外结构层。其工作原理是通过机械排风或自然压差使室内排风通过多孔层至空腔，最终排出至室外。从而可以利用排风中的冷量减少墙体的冷负荷。

图1 排风隔热墙结构示意图

为了对排风隔热墙进行高效而准确的传热模拟及负荷计算，需要对排风隔热墙的传热计算模型进行研究。本文根据傅里叶变换[3]建立了排风隔热墙的二维频域有限差分（FDFD）模型，并将该模型和排风隔热墙已有数值模型[1-2]（二维时域有限差分（FDTD）模型）进行了对比，以说明FDFD 模型的精度特点与效率提升。最后，分析了FDFD 模型离散数对模型精度的影响。

1 排风隔热墙的二维FDFD 模型

1.1 物理模型

排风隔热墙由多孔层，空腔层，外结构层组成。其基本原理为：室内排风通过多孔层，空腔层排出，从而带出从室外传人室内的热量（或冷量），降低外墙体形成的空调负荷。为简化其数学模型，对于排风隔热墙作出如下物理假设：

1）不考虑多孔材料和外层墙体材料在垂直方向的导热。

2）不考虑空腔中的空气与两侧壁面发生的辐射换热，只考虑两侧壁面之间发生的辐射换热。

3）墙体，多孔材料和空气都作为均匀介质来处理，物性参数恒定为常数。

4）空腔中的空气作为不可压缩流体处理，并且不考虑浮升力。空气的渗透流速沿着多孔材料的厚度方向和高度方向是恒定的和均匀的，且假定气流在流动过程中的湿度保持不变。

5）多孔材料内的空气与骨料达到瞬时热平衡，两者温度相同。

其存在的物理过程主要有：室内空气和多孔层的对流换热，室外空气和外结构层的对流换热，空腔空气与两侧壁的对流换热。空腔两侧壁的辐射换热。多孔层和外结构层导热。多孔层和空腔的空气对流热。

1.2 二维FDFD 模型

根据物理假设可建立排风隔热墙的二维FDTD模型[1-2]。在此基础上引入温度波的傅里叶级数分解可以推导出排风隔热墙的二维FDFD 模型。

对于一个以时间τ0为周期的温度波t(τ)，可以分解为一系列频率的正弦波的加和[3]，其复数形式表示如式（1）：

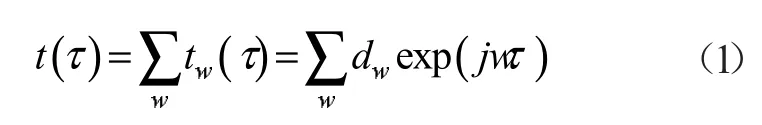
式中：dw称之为温度波的离散频谱，和频率w 有关的复数；，是虚数单位。

将式（1）应用到二维FDTD 模型中，可以得到式（2）～（8）组成的二维FDFD 模型的方程组。在此，为了书写方便，将式（1）中dw的下标w 略去。

1）多孔层水平方向上离散为n 个节点，式（2）为内节点方程。式（3）、（4）为边界节点方程。

2）空腔竖直方向上离散为y 个节点，式（5）为其节点方程。

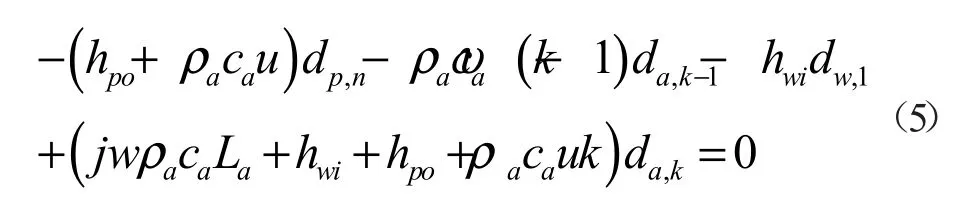
3）外结构层水平方向上离散为m 个节点，式（6）为内节点方程，式（7）、（8）为边界节点方程。

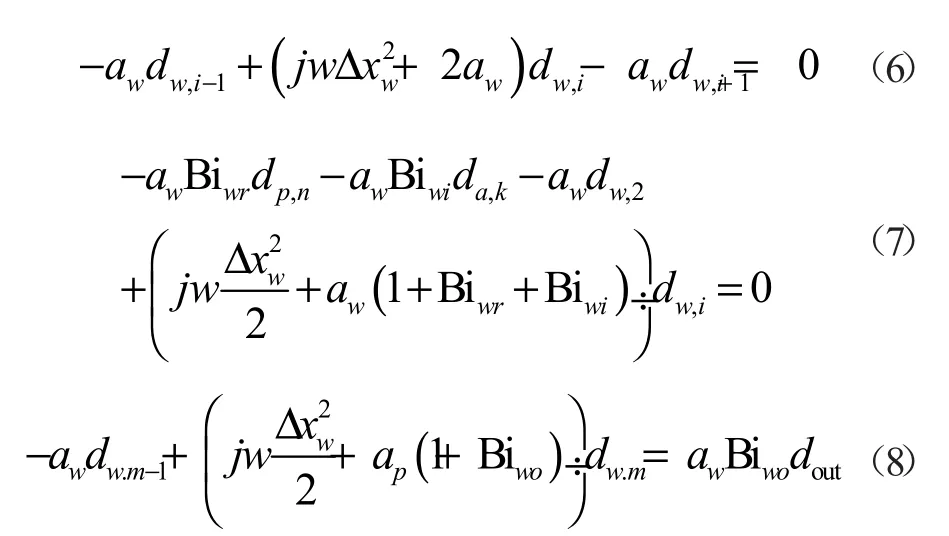
式（2）～（8）中，引入了导热系数和一些准则数；其中，a=λ/ρc，Pe=ρacauΔxp/λp，Bi=hΔx/λ；其余参数的说明：ρ代表密度，kg/m3；c 代表比热容，J/(kg·K)；λ 代表导热系数，W/(m·K)；h 代表对流换热系数，W/(m2·K)；Δx 代表水平方向相邻节点距离，m；Δy 代表竖直方向相邻节点距离，m；υ，υk分别为多孔层中空气的渗流速度和空腔中第k 个节点的空气流速，m/s。下标(p,i)，(a,k)，(w,i)分别代表多孔层，空腔层，外结构层各离散节点，下标in,out 分别代表室内温度点，室外空气综合温度点；下标a，p，w 分别代表空气，多孔材料，外层结构；下标pi，po，wi，wo，r 分别代表多孔层室内侧壁面及外侧壁面，外层结构内侧壁面及外侧壁面，多孔层外壁面和外结构层内壁面的辐射换热。

对于多孔层室内侧的对流换热系数hpi取为5.26 W/(m2·K)[4]，外结构层室外侧对流换热系数hwo取为23.26 W/(m2·K)[5]，空腔两侧的对流换热系数hpo，hwi相等，均按式（9）计算[6]：

式（2）～（9）共同构成了封闭的方程组，使某个频率w 下的din，dout作为输入，则通过二维FDFD 模型可以求出排风隔热墙各点对应频率w 下的温度波分量。如果要求出排风隔热墙各点的温度波响应，则只需要把所有频率下的温度波分量按式（1）进行加和即可，具体的求解过程可见图2。

图2 时域温度波响应的求解流程

1.3 离散傅里叶变换（DFT）

在实际问题中，一般处理的不是连续温度波，而是离散的温度时间序列，这时可采用DFT 将周期离散温度时间序列变为离散温度频率序列，采用tn(n=0,…,N-1)表示周期温度时间序列，dk(k=0,…,N-1)表示频率序列，DFT 与离散傅里叶逆变换（IDFT）如式（10），式（11）所示：

d0对应的频率分量为0 频，dk(1≤k≤N/2)对应的频率为正频率((2π/τ0)k)，而dk(k≥1+N/2)对应的频率为负频率((2π/τ0)(k-N))；当N 为偶数时，dk(k=N/2)对应频率代表着负频率；当N 为奇数时，dk(k=(N-1)/2)对应频率代表着最大的正频率，dk(k=(N+1)/2)对应频率代表着最大的负频率。

2 模型比较

将二维FDTD 模型和二维FDFD 模型（数值模型）进行比较，说明FDFD 模型的精度，计算效率以及其适用性。

2.1 模型参数条件说明

模型计算比较时取的物性参数如表1 所示，其中多孔层材料取的是玻璃纤维，外层结构取的是粘土砖。对于排风隔热墙的尺寸参数，具体如表2 所示。排风隔热墙的渗透风速取0.001 m/s。

表1 材料物性表

表2 尺寸参数表

取周期为24 h 的室内外温度波扰动，其具体如图3 所示。室外温度波的扰动参考了武汉夏季某一天的室外综合温度，室内温度波的扰动则为空调工况下的一天室内温度波动。

图3 室内外温度波扰动

2.2 FDFD 模型精度比较

以经过充分发展并且已得到验证的FDTD 模型为参考对象[1-2]，说明FDFD 模型的精度特性。

如图4 所示，表示的是根据上节所述条件，然后利用FDFD 模型和FDTD 模型计算出来的一天内的排风隔热墙室内热流密度变化，其中q 的计算式如式（12）所示。

图4 排风隔热墙热流密度变化

如图4 所示，可以看出，FDFD 模型和FDTD 模型的计算结果吻合非常好。进一步地可以汇出两者的差异曲线，如图5 所示。可以看到，最大差值也不超过0.1 W/m2，误差非常小，说明FDFD 模型计算结果是可靠的。

图5 两模型热流密度差异变化

值得说明的是，本次计算采用的节点离散数目分别是：多孔层内离散节点数n=20，外结构层离散节点数m=20，空腔竖直向离散节点数y=5。

2.3 FDFD 模型效率和计算输入

FDFD 模型为计算带来了效率上的巨大提升。以上面的计算为例，说明FDFD 模型和FDTD 模型计算时间上的差异。在处理器为Intel Core i5-7400 的计算机上，采用Python3 的编程环境进行计算，FDFD 模型相对于FDTD 模型在计算速度上快了约70 倍左右。

FDFD 模型相对于FDTD 模型的输入条件有所不同。FDFD 模型需要周期性的温度波输入条件，并且无需初始条件。而FDTD 模型需要给定初始条件，和任意的温度波边界条件。

3 FDFD 模型离散特性

FDFD 模型计算速度受到模型的空间离散程度的影响，即多孔层内离散节点数n，外结构层离散节点数m 和空腔竖直向离散节点数y。如何在保证模型精度的条件下，尽可能地减小离散节点数n，m，y。并且如果模型精度得到保证，y 降低到1，FDFD 模型从二维退化成一维，则FDFD 模型可以得到大大简化。

首先对多孔层离散节点数n 对模型结果的影响进行探究。这里，选取一天内热流密度变化的最大值作为模型结果进行比较。如图6 所示，显示的是n 分别取2，5，10，20，50，100 时的最大热流密度。此时的m=20，y=5。

可以看到n=20 时最大热流密度趋于稳定，n=20是较为理想的节点数。换算成相应的相邻节点距离表示，即多孔层内的相邻节点距离1.58 mm 左右时模型结果较为理想。

类似地对m 作如上的分析，如图7 所示，此时的n=20，y=5。可以看到m=10 时就可以保证足够的精度。相应的外结构层的相邻节点距离为22.22 mm 左右时，模型结果较为理想。

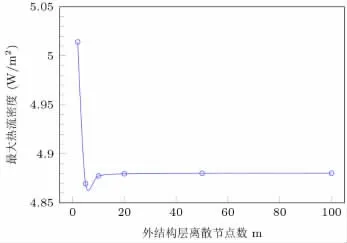
图7 不同节点数m 下的最大热流密度

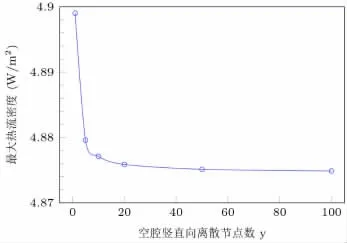
图8 不同节点数y 下的最大热流密度

对y 分别取1，5，10，20，50，100 时，结果如图8 所示。可以看到，即使y 取1，模型结果误差也不会超过0.03 W/m2。说明二维FDFD 模型即使简化成一维也不会对结果带来太大的影响。

另外，多孔层的取的节点数目n 对模型结果影响最大，应该多取一点。其次是外结构层的节点数目m。空腔竖直向的节点数目y 对结果影响最小，甚至可以简化为一个，从而将二维模型变为一维模型。

4 结论

本研究建立了排风隔热墙的二维FDFD 模型。然后将二维FDFD 模型和数值模型作了对比，说明其精度，计算效率和计算输入特点。最后分析了二维FDFD模型的离散特性，得到了如下结论：

1）二维FDFD 模型和二维FDTD 模型相比具有足够的精度，在本文的算例中，两模型计算得到的热流密度差异最大也不超过0.1 W/m2。

2）二维FDFD 模型相对于二维FDTD 模型计算速度得到了大幅度的提升。两模型的输入条件有所不同，FDFD 模型仅需要周期边界条件，而FDTD 模型需要初始条件以及任意边界条件。

3）多孔层的离散节点数目n 对二维FDFD 模型带来的结果影响较大。外结构层的离散节点数目m，空腔竖直向的离散节点数目y 对二维FDFD 模型的影响较小。

结果表明：本研究建立的排风隔热墙二维FDFD模型具有和传统的数值模型具有几乎一样的准确度，并且计算效率得到大幅度提升。