齿面形貌对齿轮系统动态特性的影响研究

李 直，王建梅，张 宏，刘 焜

(1.太原科技大学 山西 太原 030024；2.合肥工业大学 安徽 合肥 230009)

0 前言

齿轮系统作为重型机械重要的传动部件，其传动精度和使用寿命直接关系到设备的安全长效运行[1-2]。齿面啮合过程中的摩擦接触情况对于齿轮系统的传动效率和动态性能有着重要的影响，由于齿面上的接触压力、相对滑动速度和滑滚比等接触状态参数随着啮合位置而不断发生变化，由此引起了齿面摩擦系数的时变性特征[3-5]。齿轮各种加工形式会造成齿面微观形貌具有随机性，而齿面形貌对于齿面时变摩擦特性有着明显的影响作用[6-9]。作为齿轮系统功率损失的重要来源，研究由齿面形貌所引起的齿面摩擦力波动有助于改善齿轮动态性能[10-12]。

为了对啮合过程中的齿面摩擦特性进行研究，学者们开始思考如何准确获取齿面摩擦系数曲线。利用弹流润滑理论来计算获得齿面摩擦力变化情况，在计算过程中结合了齿面接触分析的计算结果，将齿面啮合接触过程各项参数代换为弹流润滑计算的输入条件，从而根据计算结果提出相应的齿面摩擦系数拟合公式[13]。鲍和云[14]基于弹流润滑理论计算得到的齿面摩擦系数，分析了齿轮系统的动态特性，并与使用库伦摩擦系数计算模型的结果进行了对比，分析表明摩擦系数的选取会显著影响齿轮沿摩擦力方向的振动。邹玉静[15]建立了斜齿轮的摩擦动力学模型，将计算结果用于润滑分析中，并将润滑分析得到的时变摩擦系数再次用于齿轮动力学分析中，发现齿面时变摩擦特性对于齿轮系统动态特性有着重要影响。陈骏霆[16]利用综合摩擦系数计算模型分析了锥齿轮啮合过程中的摩擦功率损失情况，发现不同的齿面摩擦系数模型在不同啮合区域的计算精度有明显差异，在选择时应充分考虑齿轮啮合润滑状态。Li[17-18]利用弹流润滑理论计算了几种真实齿面形貌下的摩擦特性，并以此为基础研究了齿轮系统摩擦动力学特性和疲劳寿命之间的关系。Xu[19]通过将摩擦试验结果和EHL计算结果相结合，拟合出了啮合齿面摩擦系数回归公式，从而得到了能预测齿面时变摩擦系数变化情况的Xu模型。Huang[20]利用Xu模型计算了大重合度齿轮的摩擦动力学特性，发现Xu模型能有效应用于齿轮动力学计算中。

综上所述，建立考虑齿面时变摩擦系数的齿轮动力学模型有助于研究齿面形貌对于齿轮动态特性的影响作用。本文以Xu模型为基础计算了几种不同齿面形貌参数下的齿轮时变摩擦系数，然后将其代入齿轮六自由度动力学模型中，利用Runge-Kutta法对系统微分方程组进行了求解，研究了齿面形貌对于齿轮系统在不同啮合参数情况下动态特性的影响作用。

1 齿面时变摩擦系数的计算

在啮合过程中，接触齿面处于典型的弹流润滑状态，因此利用弹流润滑相关理论对其进行计算便可获得齿面摩擦系数的变化情况。Xu在综合考虑齿面润滑状态、齿面形貌和工况条件等因素后，通过弹流润滑计算结果拟合得到了齿轮啮合过程的齿面摩擦系数回归公式，即

(1)

式中，PH为齿面赫兹接触压力；R为接触点等效半径；Sq为表面粗糙度均方根偏差；拟合参数b1～b9分别为：b1=-8.916465，b2=1.03303，b3=1.036077，b4=-0.354068，b5=2.812084，b6=-0.100601，b7=0.752755，b8=-0.390958，b9=0.620305。

由于齿轮啮合接触可认为是线接触形式，因此利用双盘摩擦试验可以对Xu模型的计算精度进行验证。试验在如图1所示的JPM-1双盘摩擦试验台上进行，具体试验设置可参照文献[21]。试验使用了三个具有相同Sq的圆盘试件作为对比，验证了在相同工况下的Xu模型计算精度，其结果如图2所示。在该工况下，Xu模型计算结果同试验结果在节点附近差别较大，而在距离节点较远的两侧区域较为一致。根据齿面啮合滑滚比的定义，在节点附近啮合时滑滚比较小，滚动摩擦占主导成分，表面形貌对于接触面间的摩擦系数的影响较大，而Xu模型中对于表面形貌的考虑仅简化为以幅度参数Sq来体现，因此造成了与试验结果的偏差。随着滑滚比的增大，Xu模型计算结果也与试验结果相吻合，这说明在滑动摩擦要素较多时，Xu模型的精度能够很好地满足计算需求。总体而言，Xu模型作为一种对于齿面时变摩擦系数快速求解的方法，能够满足本研究的计算要求。

图1 双盘摩擦磨损试验台及试件安装

图2 Xu模型结果与双盘试验结果的对比

2 齿轮动力学模型

为了更准确地研究齿轮啮合过程中的齿面摩擦力对于系统动力学特性的影响，本文使用六自由度动力学模型对齿轮系统动态响应进行计算。动力学模型示意图如图3所示，根据示意图可列出齿轮动力学微分方程组。

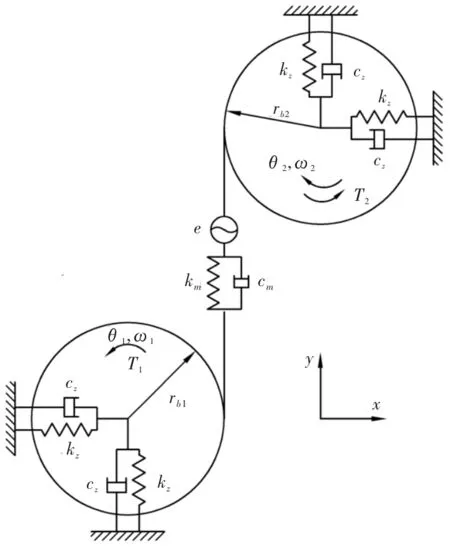
图3 齿轮六自由度动力学模型

(2)

(3)

(4)

(5)

(6)

(7)

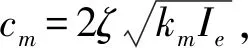
对齿轮啮合过程中的摩擦力臂和滑滚比进行计算，得到图4a和图4b，利用公式(1)即可得到图4c啮合过程中的时变摩擦系数变化情况。

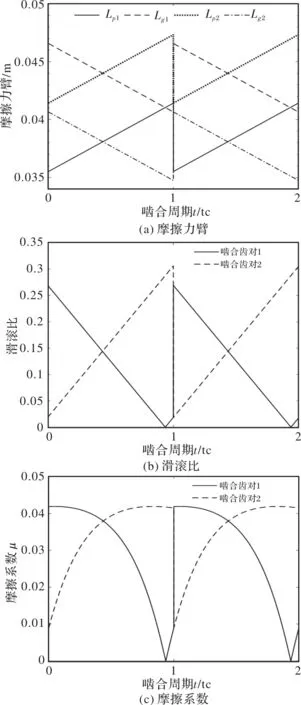
图4 齿轮啮合参数计算结果

3 结果与讨论

本次齿轮副计算参数如表1所示，计算中选取齿面粗糙度Sq分别为0.1 μm、0.5 μm和1 μm的齿轮进行对比，将利用Xu模型得到的时变啮合摩擦系数代入图3的动力学模型中进行计算，求解过程采用Runge-Kutta法，计算约300周期后输出结果。

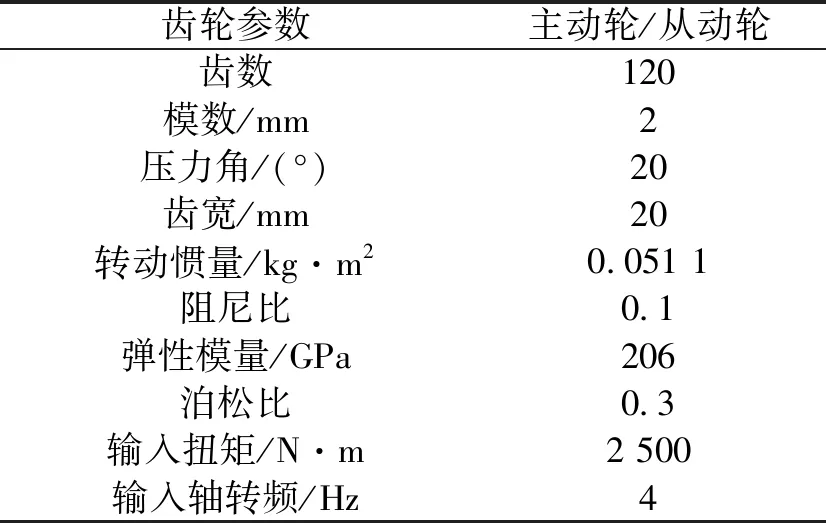
表1 动力学计算中的齿轮副参数

3.1 齿面形貌对动态性能的影响方向

动态传递误差(DTE)作为齿轮动态特性的重要参数，常用来衡量啮合线方向(LOA)齿轮振动情况。图5a是该工况下不同齿面形貌齿轮DTE图谱，可看出三种齿轮DTE基本一致，导致图5b中不同齿面形貌齿轮动态啮合力的差别也较小，说明齿面形貌对于LOA方向齿轮动态性能的影响比较微弱。但是从图5c中可发现齿面形貌对齿面摩擦力有显著影响，且随着齿面粗糙度增加，齿面摩擦力也有明显增加，说明齿面形貌对于齿轮动态性能的作用主要体现在对齿面摩擦力的影响上，因此齿面形貌对于齿轮动态特性的影响也发生在齿面摩擦力作用的啮合线垂直方向(OLOA)。

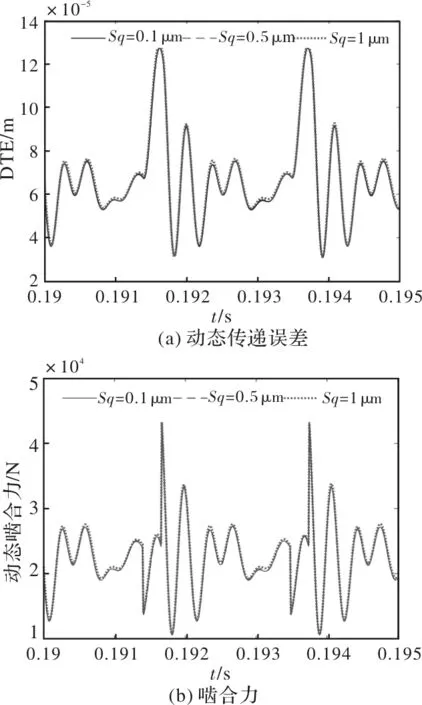
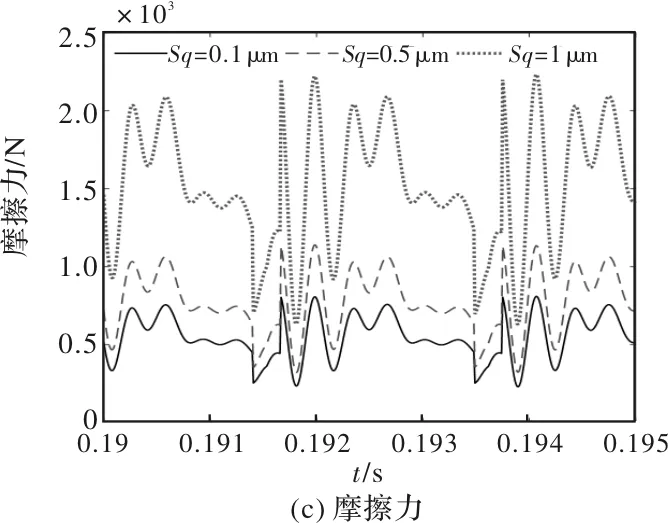
图5 不同齿面形貌齿轮的啮合过程DTE及受力计算结果

3.2 齿面形貌对动态响应的影响

结合本文不同齿面形貌齿轮的啮合过程DTE及受力的分析，本文主要研究齿面形貌对齿轮OLOA方向动态特性的影响。图6是不同支承刚度和支承阻尼情况下的不同齿面形貌齿轮OLOA方向振动位移时间历程图。从图6a中可看到随着支承刚度的增大，齿轮OLOA方向振幅在明显减小，而齿面粗糙度越大、振动幅值越大的趋势依然存在于各个支承刚度下。从图6b中可看到支承阻尼对于振动幅值的影响十分微弱，远不如齿面形貌所造成的影响明显。从图7和图8的各工况齿轮系统运动相图中可发现支承刚度变化情况下除了振动幅值随支承刚度增大而减小，系统运动状态周期性也有明显改变，即随着支承刚度的增大，相图中的封闭环数量也在增加，而支承阻尼变化时，系统运动状态并没有发生明显改变。图9和图10是不同工况下各齿面形貌齿轮系统的庞加莱图，在支承刚度增大后庞加莱点分布更加集中，说明与支承阻尼对于齿轮系统动态特性的微弱作用不同，三种不同齿面形貌的齿轮系统周期性和稳定性都在支承刚度增大的过程中得到了改善。

图6 不同工况下各齿面形貌齿轮的OLOA方向振动位移时间历程图

图7 支承刚度变化情况下的不同齿面形貌齿轮OLOA方向动态响应相图(cz =2000 Ns/m)

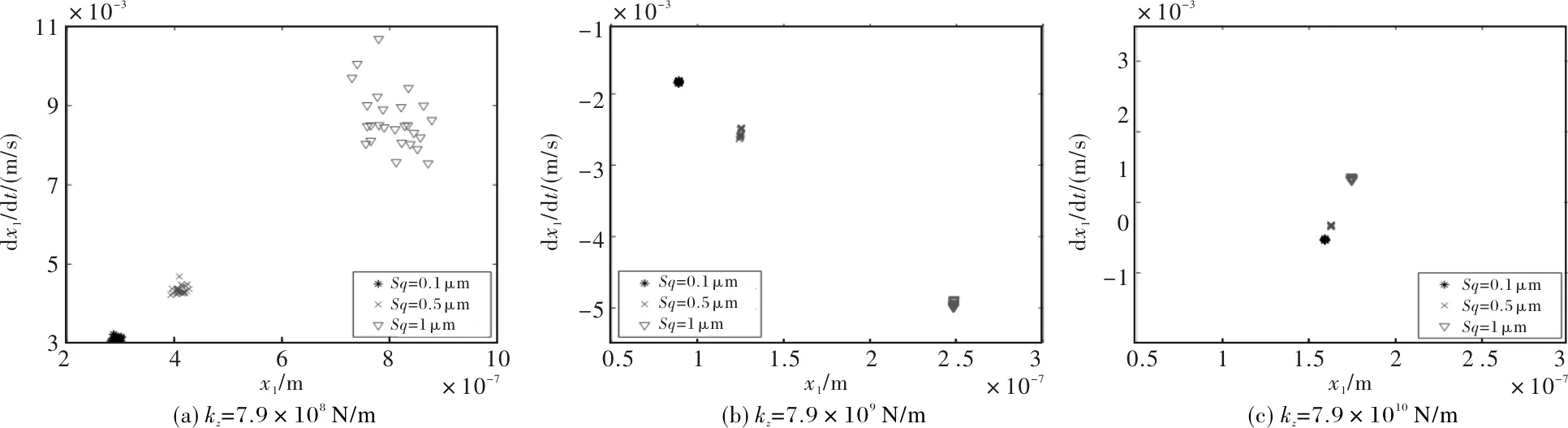
图9 支承刚度变化情况下的不同齿面形貌齿轮OLOA方向动态响应庞加莱图(cz=2000 Ns/m)

图10 支承阻尼变化情况下的不同齿面形貌齿轮OLOA方向动态响应庞加莱图(kz=7.9×107 N/m)

为了研究支承刚度和支承阻尼对齿轮振动频域特征的影响，图11和图12给出了支承刚度和阻尼变化情况下的齿轮OLOA方向振动响应频谱图。从图11中可看出随着支承刚度的增加，相同啮合频率三种不同齿面形貌齿轮振幅相差幅度在逐渐减少，说明在弹性支承转变到刚性支承的过程中，有效削弱了齿轮OLOA方向由于齿面摩擦而产生的振动幅值。同时可发现，随着支承刚度的增大，齿轮振动的倍频数量也在增加，这也同图7中的相图形态相对应。从图12中可看出支承阻尼对于齿轮系统频域特性同样影响较小，而在相同啮合频率的不同齿面形貌所造成的振动幅值差异也没有因支承阻尼的增大而改变。

图11 支承刚度变化情况下不同齿面形貌齿轮OLOA方向动态响应频谱图(cz=2000 Ns/m)

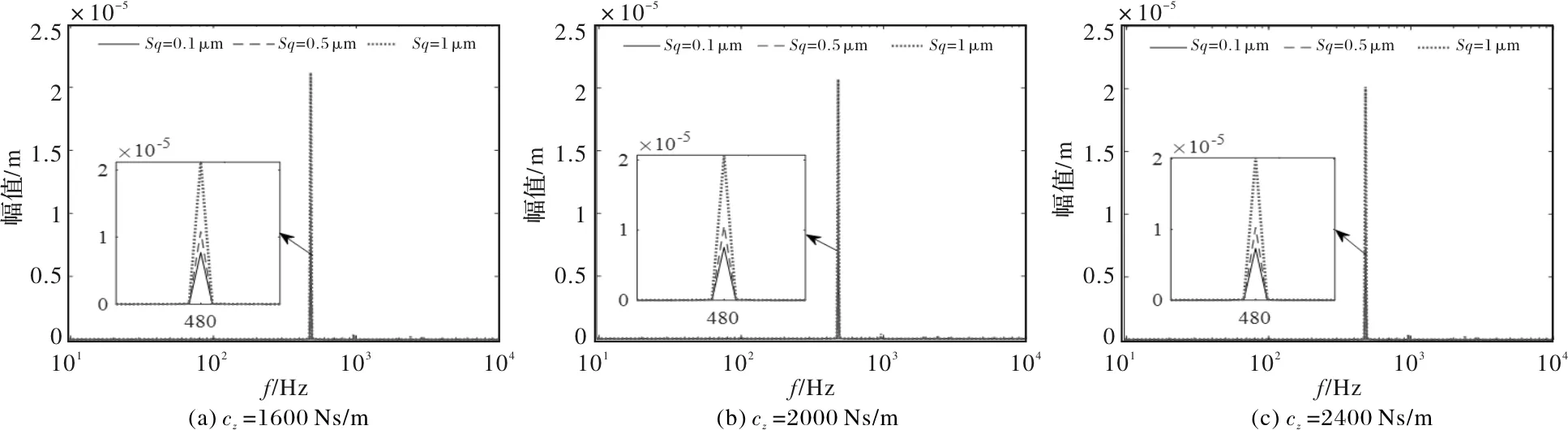
图12 支承阻尼变化情况下不同齿面形貌齿轮OLOA方向动态响应频谱图(kz=7.9×107 N/m)

4 结论

在齿轮啮合过程中，齿面磨损和齿面变形是造成齿面形貌发生改变的主要因素，这种改变反映在齿面形貌的三维形貌参数上，为了获取齿面形貌与齿轮动态特性之间的关系，本文通过将Xu模型引入齿轮六自由度动力学模型研究了不同齿面形貌齿轮的动态特性及其影响因素，得出了结论：

(1)齿面形貌对于齿面摩擦力的影响相比对于齿轮动态传递误差和动态啮合力的影响明显得多。齿面形貌对于齿轮动态特性的影响主要体现在齿面摩擦力作用的OLOA方向。在该方向上，不同齿面形貌齿轮的差别十分明显，形貌参数Sq较大的齿轮具有较大的振动幅值。

(2)相比于支承阻尼，支承刚度能有效降低OLOA方向齿轮振动幅值，削弱齿面形貌对于齿轮动态特性的影响作用，改善系统的稳定性，但是增大支承刚度也会使系统响应周期随之增多。

结论表明，齿面形貌导致的齿面摩擦力差异对于齿轮动态特性有着明显的影响， 而增加齿轮系统支承刚度能有效减轻这种影响，在以后的研究中应结合试验手段继续深入探索齿面形貌与齿轮动态特性之间的相互联系。