基于不可用性及表决机制的探测器优化布置

张景康，王海清，姜巍巍，齐心歌

（1 中国石油大学(华东)安全科学与工程系，山东青岛266580；2 中国石化青岛安全工程研究院，山东青岛266071）

火灾和气体探测系统（fire and gas system，FGS）是过程工业的重要安全屏障之一[1]，能够在火灾和气体泄漏初期进行高效的探测，从而启动相应的应急程序减小事故的危害。然而现行的探测器布置标准多基于传统的经验，无法满足工业应用的实际需求。根据英国安全和健康执行局（The Health and Safety Executive，HSE）的统计，在英国北海作业的海上油气设施发生的油气泄漏事件中，仅有约60%的气体泄漏被探测到[2]。

得益于计算流体动力学技术的发展，近年来国内外学者基于工艺设备泄漏扩散的模拟对这一问题进行了改善。Richart 等[3]通过对气体扩散范围进行评估从而确定最佳的气体传感器布置。Lee 等[4]开发了一种能够最大限度降低风险目标从而生成合理布置方案的动态迭代规划算法。Legg 等[5]基于对泄漏扩散后果模拟提出探测器布置的随机规划SP 模型和SPC模型，旨在满足覆盖约束的条件下使总探测时间最小化。王海清等[6]建立以搜索最短探测时间及附近解集为目标的SGA模型，实现不同安装高度的探测网络达到场景全覆盖以及探测时间最短。

然而在实际应用中火气探头易受单个杂散源或单个组件电子设备故障影响产生虚假报警，虚假报警造成火气系统的误动作及停车会给企业造成巨大的损失[7]。为了避免由于误报警带来的问题，通常用多个探测器表决的方式对泄漏探测进行确认。除了表决问题，探测器系统由于老化以及维修等导致的失效问题也需要进行考虑。

为了解决探测器失效的问题，章博等[8]在对模拟场景聚类缩减的基础上开发了考虑失效情景的探测器布置模型。此外考虑到探测器的表决机制和失效问题，Benavides-Serrano 等[9]利用二项分布为每个探测器分配相同的失效概率构建模型，通过多级探测减小探测系统的误报率，从而提升探测系统的可靠性；根据实际应用中不同位置的探测器受不同因素影响产生不同的失效概率，Benavides-Serrano 等[10]在后续研究中为每个探测器独立分配失效概率，以两级备用探测器为基础建立优化模型得到最佳布置方案；Liu 等[11]基于对探测器非均匀不可用性的研究提出考虑非均匀不可用性和冗余检测数学模型，通过开发一种多树求解方法解决全局优化问题得到最佳布置方案；Rad 等[12]根据泄漏后果与发生概率构建基于风险的探测器布置优化模型，通过将泄漏风险降低至所需水平对探测器布置进行改进；此外Rad等[13]基于表决机制提出最大覆盖模型MCLPm和探测时间最小化模型SP-Vm，通过与前期未考虑表决问题的模型进行对比验证了扩展机制的必要性和重要性。

以上研究虽然考虑了探测器失效以及表决问题，但这些研究多基于单个探测器失效进行考虑，通过预先设定探测器的失效模式得到探测器布置优化模型。然而实际应用中探测器构造复杂，简单的失效模型假设无法反映实际应用情况，此外探测器单元由探测器、表决系统和辅助系统（逻辑器、供电系统）等多个部分组成，单独考虑探测器的失效不符合实际需求，因此需要根据实际对表决系统整体的失效进行研究。

本文在充分考虑探测系统单元失效以及表决问题的基础上，通过分析表决系统在工作时的逻辑回路获得各回路的探测时间，结合相关标准与挪威PDS（Palitelighet og tilgjengelighet av Datamaskinbaserte Sikringssystemer）数据库的真实失效数据求出每种单元的需求失效概率（probability of failure on demand，PFD），提出了基于不可用性及表决机制的探测器优化布置模型，并利用工艺模拟的泄漏扩散数据对其场景探测的有效性进行验证。

1 气体探测单元的失效概率与探测时间

探测器布置问题属于博弈论中的设施选址问题，该问题的实质是在一些已知位置对象的基础上运用科学的方法确定设施的位置，并使安置代价和对象间的交互代价尽量小[14]。而考虑探测系统失效的问题可以看作不确定性选址问题，这一类问题通常考虑设施因自然或人为原因而无法正常提供服务的场景[15]，与探测系统失效问题有许多相同之处。但是具体到本文的情况仍有两个问题需要解决。

1.1 探测系统需求失效概率

不确定性选址问题通常仅考虑单个设施无法提供服务的情况，而对于探测系统来说存在表决问题，其失效可以用不可用性进行表示。不可用性指系统应该执行其设定功能时未能准确执行的概率，其除了考虑系统组件的随机失效问题还包括由于预防性维修和测试导致系统离线的情况，因而更能反映系统真实的应用需求。探测表决系统由传感器、逻辑器、供电系统等组成，与安全仪表系统一样，其各组成部分均会对系统的失效造成影响，在求解其失效概率时需对各部分进行考虑。对于这一问题，IEC61508 和ISA84.00.02 针 对1oo1、1oo2、1oo2D、2oo2 和2oo3 等系统均给出了相应的指导[16-17]。此外，KooN系统的通用求解公式见式(1)[18]。

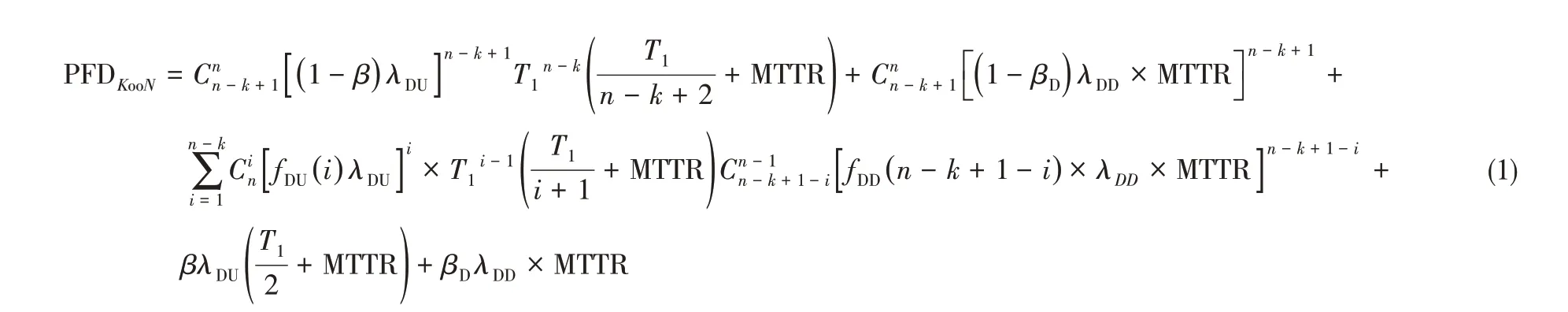
式中，T1为检验测试时间间隔；MTTR 为系统平均恢复时间；β为具有共同原因的没有被检测到的失效分数；βD为具有共同原因已被诊断测试检测到的失效分数；λDD和λDU分别是检测到的和未检测到的子系统通道每小时的危险失效率；fDD和fDU分别是考虑共因失效时检测到和未检测到的危险失效因子。

1.2 表决回路可用性和泄漏探测时间

对于单个探测器来说，其探测时间为泄漏发生到其周围泄漏气体达到报警浓度的时间（含探测器的响应时间）。而对于表决系统来说在同一火气分区内的多个分布于不同位置的探测器，其探测时间需要根据能够探测到泄漏的探测器数量和表决逻辑来定。不失一般性，以1oo3 探测系统为例，假定有3个探测器能探测到某泄漏场景，根据系统中各独立探测器的探测时间长短，将探测器分别标记为一级、二级、三级探测器。其对应探测时间分别记为t1、t2、t3，且t1≤t2≤t3，则该探测系统的表决过程如图1所示。

1oo3表决系统表示在3个探测单元中有任意一个探测单元探测到泄漏即可触发FGS。根据逻辑图，当一级探测单元可用时，由于其探测时间t1最小将直接触发FGS，因此无需考虑二级、三级探测单元的可用情况。即使二级和三级探测单元可用且成功探测到泄漏，由于t2、t3大于t1，在未参与表决的情况下系统即已触发最终动作。对应逻辑图分别为(1)(2)(3)(4)回路，此时的表决系统与二级三级探测单元无关，可以看作1oo1 系统，其可用性为1-PFD1oo1，相应的探测时间为t1。

当一级探测单元失效而二级探测单元可用时，与一级探测单元可用情况相似，此时无需考虑三级探测单元，对应逻辑图分别为图1中(5)(6)回路。由于(1)(2)(3)(4)(5)(6)回路共同构成1oo2 系统可用的所有情况，因此(5)(6)回路可以看作在1oo2 可用系统去除1oo1可用回路的情况，其可用性为（1-PFD1oo2）-（1-PFD1oo1）=PFD1oo1-PFD1oo2，相应的探测时间为t2。同样还可以得到在一级和二级探测单元均失效时，对应回路(7)的可用性和探测时间分别为（PFD1oo2-PFD1oo3）、t3。

由此推广到KooN 系统可知，在其表决过程中共有N-K+1级探测表决情况。基础级为KooK系统，对应的可用性和探测时间分别是（1-PFDKooK）、tk。当表决系统在前K个探测器中每增加1个探测单元失效，其探测等级就相应增加1级。当有r个探测单元失效时探测等级将增加r级，对应的探测回路可用性和探测时间分别为（PFDKoo(K+r-1)-PFDKoo(K+r)）、tK+r。

2 算法设计

2.1 探测器布置优化模型

根据以上对表决系统的分析，得到的基于不可用性及表决机制的探测器优化布置模型如式(2)～式(7)。

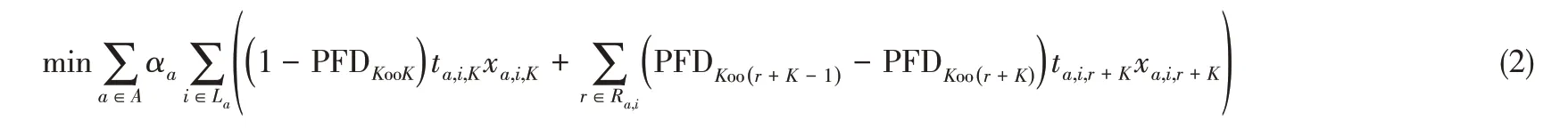
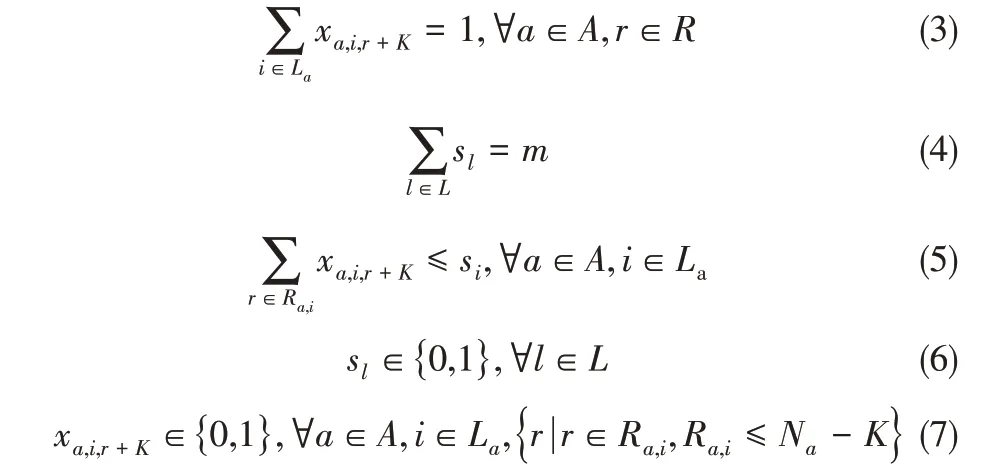
式(2)为目标函数，表示基于场景概率以及可用性和探测表决等级考虑的总泄漏场景探测时间最小化。其中r表示在基础探测等级基础上探测单元失效的个数，同样也表示增加的探测等级数，当探测表决为KooK 基础级时r 为0。PFDKoo(K+r)表示Koo(K+r)表决系统的需求失效概率，当r为0时表示基础表决系统KooK的需求失效概率。ta,i,r+K表示在r探测等级时位于i 处的r+K 级探测器探测到场景a所用的时间。同样ta,i,K是r=0 的情况，此时的探测等级为基础级。Ra,i表示泄漏场景a设定的探测等级上限，且Ra,i不超过能够探测到泄漏场景a 的探测单元总数Na与参与表决的探测器数量下限K 的差。αa表示泄漏场景a 发生的概率，xa,i,r+K表示在r 探测等级时位置i 处的探测器是否探测到场景a（探测到时xa,i,r+K=1，否则为0）。

式(3)确保每个场景a 在每个r 探测等级下都能够被探测到，式(4)表示探测器的数量为m，变量sl表示探测器存在与否，sl=1 表示该位置有探测器，sl=0表示该位置缺少探测器。式(5)表示只有已布置的探测器才有可能作为不同场景的各级探测回路。

在实际应用中表决系统的需求失效概率PFDKooN通常较小，一般为1×10-2以下（即安全完整性等级SIL2或以上等级的探测器）。当单个探测单元的失效概率较小时，表决系统的探测等级r越高，其代表的回路可用性（PFDKoo(K+r-1)-PFDKoo(K+r)）越小。在达到特定等级时其可用性趋近于零可以忽略不计。因此本文将Ra,i定为3，即考虑3个探测单元失效的情况，同时将参与表决的探测单元数量下限K定为2，此时目标函数的展开式见式(8)。

式中第1项表示基础探测等级可用时的探测时间，后3项依次表示在前一级探测单元失效的情况下次级探测单元可用时的探测时间。

2.2 探测器布设位置求解算法

构建的优化公式是一个混合整数规划模型，属于组合优化中的p-中值问题。对于这一类问题很难在有限的时间空间内求出问题最佳解，通常随着约束的增加，问题难度进一步加大，传统方法会出现因输入样本数目增大而无法计算的限制，需要采用更先进的启发式算法进行求解[19]。作为智能算法的一个重要分支，遗传算法在求解多参数、多变量、多目标和多区域但联通性较差的NP-hard问题表现出更好的性能[20]，因此本文选择遗传算法对该问题进行求解，具体的算法流程如下。

（1）以候选探测器系统的位置编号为基因，每个染色体由m个位置编号组成，代表一种探测器布置方案，采用等概率分配基因方法生成一定规模初始种群，种群规模可根据式(9)确定[20]。

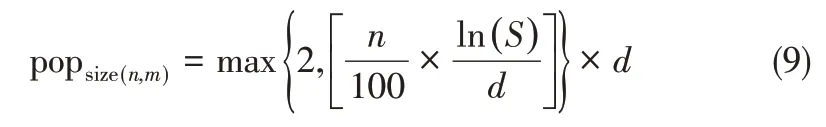
式中，n 代表候选探测器位置总数，m 为探测器最大安装数量，S = Cnm，d =[n/m]。

（2）以目标函数和探测器数量及位置约束条件为基础构造评价函数，计算种群各染色体适应值，即各布置方案的总场景探测时间。

（3）构造适应度轮盘，以计算的适应值为对象对染色体进行筛选，淘汰适应值较大的染色体。

（4）根据设定的染色体交叉、变异概率值对筛选后的部分染色体进行交叉、变异操作，生成新的染色体构成新种群。

（5）重复步骤(2)～(4)，直到种群染色体稳定不再变化，最后的染色体就是最终的探测器布置方案，适应值为最终目标函数值。

3 LNG接收站算例分析

3.1 模拟条件及参数设定

本文选定某液化天然气（LNG）接收站的气化单元作为研究对象，模拟其发生泄漏的气体扩散情况。通过危险源辨识确定危险区域，以真实工艺主要设备的几何形状为基础，随机改变工艺装置的泄漏位置、泄漏孔径和天气等条件共生成256个不同的泄漏扩散方案。需要指出的是，本文的重点并不在于典型泄漏场景的识别与泄漏扩散模拟，这里获得仿真场景的泄漏浓度时间分布数据，仅是为了验证上述所提出的探测器布设算法的有效性。

在模拟过程中，当甲烷气体浓度达到燃烧下限的25%时认为探测器探测到泄漏场景。此外每个场景被赋予了相同的概率，因此对于公式中的所有场景a∈A，αa是相同的。

根据挪威PDS数据库的失效数据，结合现场运行情况，确定探测器相关参数为：检验测试时间间隔为半年、平均恢复时间为8h，失效率λ 为5×10-5h-1，被探测到失效分数β 为20%，诊断覆盖率DC 为60%。以2ooN 表决系统为例，分别求出2oo2、2oo3、2oo4、2oo5系统的需求失效概率，利用遗传算法计算得到在不同探测器数量下的布置方案。

3.2 算例求解与结果

实验运行环境为：CPU3.5GHz，4G 内存，利用Matlab 软件实现算法编程。染色体交叉概率pc为0.9，迭代次数为10000次，表1是探测器数量分别为21、25、30时的结果。

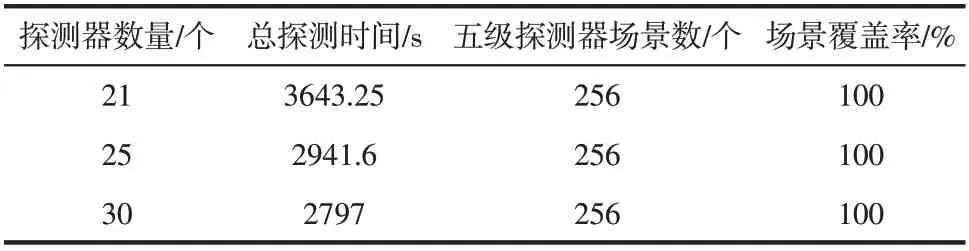
表1 不同探测器数量条件下探测时间表

从表1中可以看出，不同探测器条件约束下的布置方案均能成功探测到各泄漏场景，能够保证对各泄漏场景的五级探测，满足模型要求。此外在探测器数量较少时，每个探测器为了能够探测到更多的场景数会引起探测时间的增大，从而导致各探测器的总探测时间较大。随着探测器数量的增加，每个探测器需要覆盖的场景数有所减少，对各场景的探测时间随之变小，从而使得总场景的探测时间从3643.25s减小到2797s。

图2 是在不同探测器数量下的总探测时间图。从图中可以看出随着探测器数量的增加，总场景的探测时间不断减小。但随着探测器的布置渐趋合理，增加更多的探测器对各探测器的探测时间影响有限，从而使得总探测时间的减小幅度逐渐变小。此外增加额外的探测器会造成成本的增加，因此要通过计算确定合理的布置方案。

图3(a)、(b)分别是探测器数量为21 和30 时，11～40 号场景各级探测单元对应的探测器探测时间图。从图中可以看出，两种方案都能满足预期的要求，各场景都至少被5个探测器探测到。能够保证在3个探测单元失效的情况下仍有2个探测单元进行表决，从而正常触发FGS。与总探测时间的变化一样，探测器数量较少时会得到较大的探测时间。从图中可以看出探测器数量为21 时其各级探测时间总体大于等于探测器数量为30 时各级的探测时间。并且随着探测器级别的增大，各级探测器之间的探测时间偏差不断变大。

图2 探测器数量与总探测时间关系

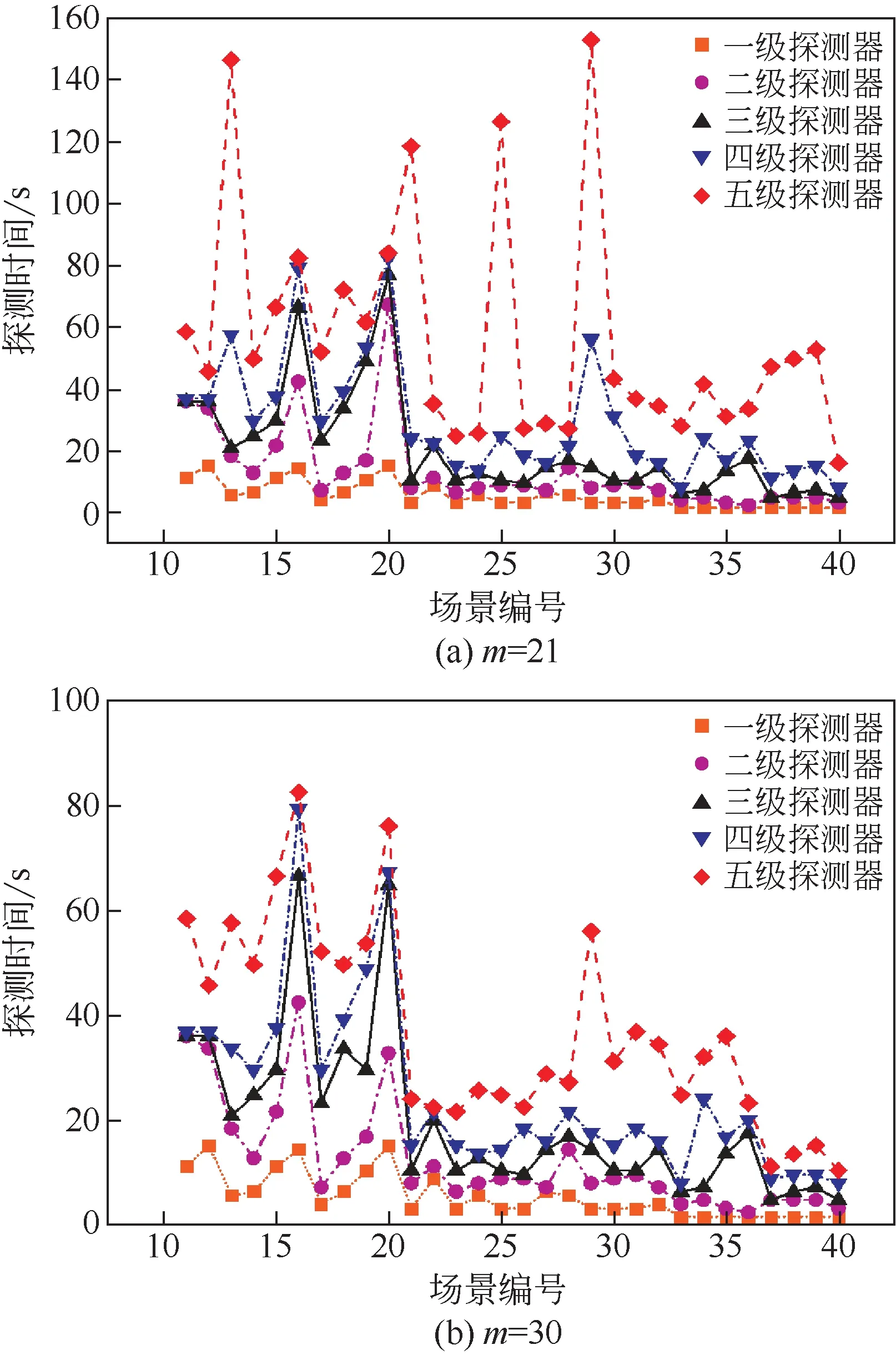
图3 不同级别探测器场景探测时间

图4是不同探测器方案下拥有不同级别探测器的场景数量分布图。在探测器数量相同时，随着探测器级别的增加，拥有该级别探测器的场景数逐渐减少。例如在探测器总数为21 时，拥有六级探测器的场景数为227个，而拥有十级探测器的场景数为78 个。在同一级别中，随着总探测器数量的减少，拥有该级别探测器的场景数量同样减少。例如当探测器总数为30 时拥有十级探测器的场景数为146，约等于探测器总数为21时拥有十级探测器场景数量的两倍。因此如果在实际应用中考虑更多的探测单元失效问题，需要增加更多的探测器确保方案的可行性。

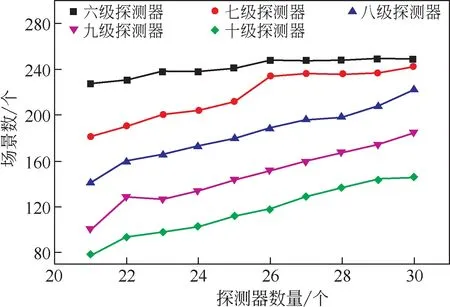
图4 不同探测器方案下各级探测器场景数量

4 结论

本文以火气系统探测器优化布置为对象，针对探测单元失效以及表决问题，基于表决系统需求失效概率和探测时间提出合理的数学模型，利用模拟的泄漏场景数据对模型进行检验，验证了该模型的有效性。

关于探测器优化布置仍存在很多困难需要解决，本文的优化模型中假定各系统的需求失效概率相同，然而在实际中探测系统需求失效概率会因为维修、安装等条件的不同存在差异；此外基于优化的方法依赖模拟的全面性而需要耗费大量的计算时间，不利于此方法的实际工程化应用，这些问题将是后续的重点研究内容。

符号说明

A={1,2,…,256} —— 泄漏场景集合

a —— 泄漏场景编号

DC —— 诊断覆盖率

f —— 危险失效因子

i —— 探测器位置编号

K —— 参与表决的探测器数量

L={1,2,3,…} —— 候选探测器位置集合

La={1,2,3,…Na} —— 受泄漏场景a 影响的探测器候选位置集合

MTTR—— 系统平均恢复时间，s

m—— 探测器安装数量

Na—— 能够探测到泄漏场景a的探测器数量

pc—— 染色体交叉概率

popsize—— 初始种群规模

R —— 探测单元等级

sl—— 表示l处是否有探测器安装的二值变量

T1—— 检验测试时间间隔，s

ta,i,r+K—— 气体泄漏探测时间

xa,i,r+K—— 表示i 处探测器是否探测到泄漏场景的二值变量

αa—— 泄漏场景a发生的概率

β —— 失效分数

λ —— 失效率