考虑黏温系数的蒸汽吞吐递减率多元回归模型

王树涛 张风义 张彩旗 刘 东 张国浩

中海石油(中国)有限公司天津分公司, 天津 300459

0 前言

海上稠油热采开发投资大、风险高,热采方案研究、跟踪评价和产量规划等工作都需要明确蒸汽吞吐周期内的产量递减情况[1-3]。递减法作为一种常用的油藏工程方法,既方便又实用,已知热采的高峰产能和递减率,就可以预测整个周期的生产动态,但是不同油藏参数和注汽参数下的周期内递减率不同[4-6]。目前相关方面的定量研究较少,已有的蒸汽吞吐递减率预测模型仅考虑了油藏静态和注蒸汽动态参数的影响,并未考虑稠油流体黏温系数的影响,造成具有不同流变特征的稠油油田蒸汽吞吐递减率预测准确率差异大[7-8]。

渤海LD油田明化镇组储量规模较大,属于典型的河道型浅水三角洲沉积,高孔高渗型储层。但由于地层原油黏度为 2 336 mPa·s,冷采试采井效果差,水平井冷采比采油指数仅为0.5 m3/(d·MPa·m),预测采收率仅7%左右,不能满足海上油田高效开发的需要。借鉴渤海NB油田稠油热采成功经验,开展了LD油田蒸汽吞吐先导试验研究,除了经济效益因素,主要试验蒸汽吞吐开发的周期内有效期和增油量。LD油田第一井次蒸汽吞吐试验,由于受注热参数不达标、储层和流体性质差异等因素影响,周期内递减率远超预期,导致热采有效期大幅缩短,严重影响海上作业计划,并影响投入产出比考核。

为了能够在考虑尽可能多因素情况下准确预测蒸汽吞吐递减率,有必要开展考虑黏温系数影响的蒸汽吞吐递减率多元回归模型研究。

1 稠油黏温系数探讨

在渤海油田开展蒸汽吞吐先导试验的过程中,发现LD和NB两个油田周期内递减率(统计每30 d的日产油量变化率，后同)分别为26.6%和3.3%,周期内递减率差异较大,而仅考虑常规油藏和注汽参数情况下无法解释这个差异[9-10]。通过对比LD与NB油田稠油黏温曲线,发现LD油田比NB油田的原油黏度对温度更敏感。为了定量表征原油黏度对温度的敏感性,引入了ASTM黏温公式中的黏温系数概念[11-12]。式(1)可以将黏温关系转化为线性关系,黏温系数可以直接反映原油黏度对温度的敏感程度大小。

lglg(μ+0.8)=lglg(μ0+0.8)-nlg(T/T0)

(1)

式中:n为黏温系数;T为温度,℃;T0为已知温度,℃;μ为温度T条件下的黏度,mPa·s;μ0为温度T0条件下的黏度,mPa·s。

统计陆地和海上17个油田的黏温曲线,发现不同油田原油对温度的敏感性差异较大,黏温系数范围0.3～0.9,不同黏温系数下的黏温曲线见图1。

图1 不同黏温系数稠油的黏温曲线对比图Fig.1 Comparison of viscosity-temperature curves of heavy oils with different viscosity-temperature coefficients

石油分散系统以沥青质为核心,以附于它的胶质为溶剂化层而构成的胶束组成分散相,烃类油分和部分胶质组成分散介质,有关研究表明原油的黏温系数主要与胶质沥青质含量及分子结构有关[13]。结合上述17个油田的统计数据,稠油黏温系数与胶质沥青质含量有较好的相关关系,见图2。不同稠油油田油样的胶质沥青质含量差异大,因此,在预测蒸汽吞吐周期内递减率的时候,不能忽略稠油样品对温度敏感性的影响,应该将黏温系数作为主要影响参数之一加以考虑。

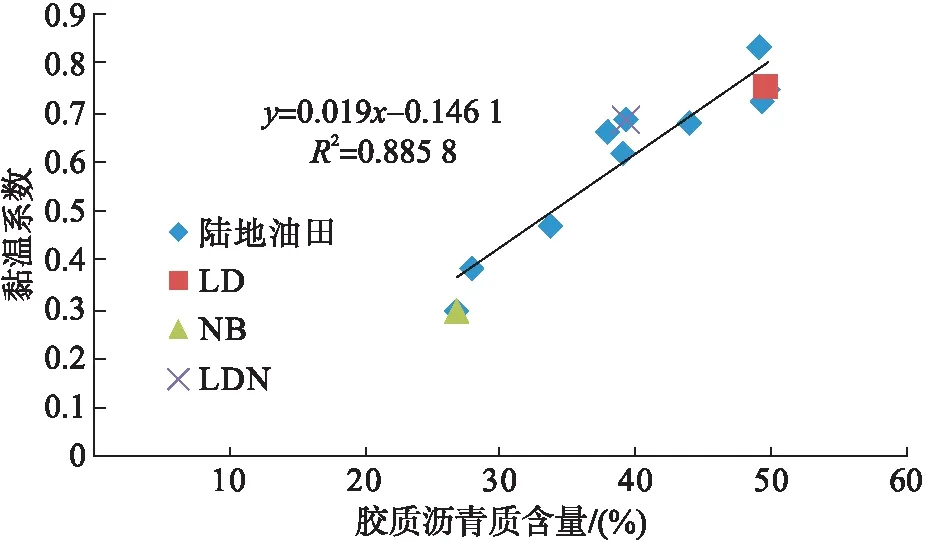
图2 稠油黏温系数与胶质沥青质含量关系图Fig.2 Relationship between viscosity-temperature coefficient of heavy oil and content of resin-asphaltene

2 蒸汽吞吐周期递减率多元回归模型建立

在单因素影响规律研究基础上,结合油藏数值模拟和正交试验设计方法产生多元回归样本集,再通过多元非线性回归方法得到蒸汽吞吐递减率的预测新模型,并验证模型可靠性。

2.1 蒸汽吞吐递减规律及影响因素研究

2.1.1 蒸汽吞吐周期内递减规律分析

为了分析蒸汽吞吐周期内的递减规律,需要借助热采精细数值模拟技术,研究井筒周围加热区温度场和原油黏度的变化规律。以渤海蒸汽吞吐先导试验区油藏和流体参数为原型,建立概念模型:油藏中深 1 287 m、原始地层压力12.6 MPa、油藏温度52 ℃、地下原油黏度 2 336 mPa·s、油层厚度10 m、初始含油饱和度0.72、平面渗透率 3 786×10-3μm2,平面网格尺寸30 m(井周围加密到1 m),纵向网格尺寸1 m,注汽温度300 ℃,注汽干度0,周期注汽量 3 000 m3。该模型与A 22 H井实际的井底流压、含水率、井口温度和井底流温等参数拟合较好,能够较准确地反映蒸汽吞吐周期内的温度场和原油黏度变化规律,见图3。

a)温度a)Temperature

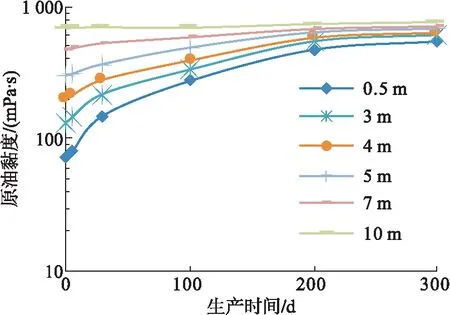
b)地层原油黏度b)Oil viscosity

在焖井后的蒸汽吞吐正常生产阶段,加热区温度场主要表现出两个特点,一是近井地带温度下降速度快,呈现明显的指数递减规律,90 d时间内温度就能下降50%左右;二是加热区温度沿远离井筒方向下降也很快,加热半径只有10 m左右(以大于地层原始温度为准)。对比加热区的温度场和原油黏度场变化可知,在相同油藏和流体条件下,原油黏度场变化规律主要受温度场变化规律影响,而原油黏度场的变化规律又会直接反映到产量递减规律的变化上,因此,蒸汽吞吐周期内产量递减率也符合指数递减规律[14-16]。

2.1.2 单因素影响相关关系研究

需要分别研究黏温系数、油藏静态参数和注汽动态参数与递减率的单因素相关关系。黏温系数为原油的固有性质,而油藏静态参数和注汽动态参数主要通过影响加热区温度场的分布范围和下降速率来影响蒸汽吞吐周期内递减率。

2.1.2.1 黏温系数影响

理论和实践都表明,蒸汽吞吐周期内递减率对黏温系数非常敏感。黏温系数属于原油内在因素对产量递减规律的影响,在相同的加热区温度场情况下,黏温系数越大,原油黏度场变化越剧烈,相应的产量递减率也越大。通过单因素相关关系研究可知,蒸汽吞吐周期内递减率与黏温系数呈指数关系,见图4。

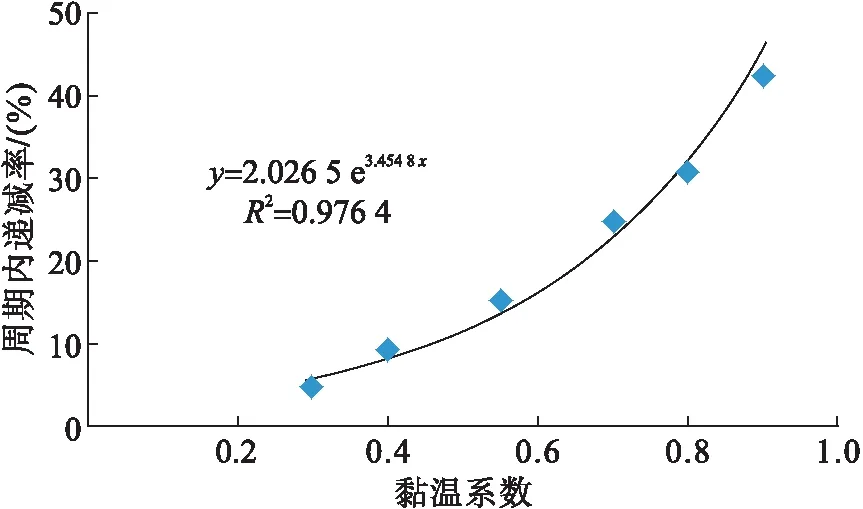
图4 黏温系数与蒸汽吞吐递减率的单因素关系图Fig.4 Single factor relationship diagram between viscosity-temperature coefficient and steam stimulation decline rate

2.1.2.2 油藏静态参数影响

原油黏度越大,温度场分布范围越小,加热区热量越快地随流体采出,产量递减率就越大,蒸汽吞吐周期内递减率与原油黏度呈二次式相关关系;油层厚度越大,加热区向顶底层的热散失速度越小,产量递减率就越小,蒸汽吞吐周期内递减率与油层厚度呈乘幂相关关系;渗透率越大,加热区热量就越快地随流体采出,产量递减率就越大,蒸汽吞吐周期内递减率与渗透率呈对数相关关系。

2.1.2.3 注汽参数影响

注汽动态参数越理想,热采效果肯定越好,但加热区与顶底层的温度差也越大,向顶底层热散失越快,导致蒸汽吞吐周期内递减率加大。通过单因素相关关系研究可知,蒸汽吞吐周期内递减率与注汽温度呈指数相关关系;蒸汽吞吐周期内递减率与注汽干度呈二次式相关关系;蒸汽吞吐周期内递减率与周期注汽量呈对数相关关系。

2.2 多元回归样本集的产生

通过正交实验设计方法和数值模拟概念模型运算生成144套样本,其中拟合样本132套、检验样本12套[17]。参考渤海海域稠油油藏条件,选取原油黏度、黏温系数、油层厚度、渗透率、注汽温度、注汽干度和周期注汽量等7个参数,各参数分别划分为6个水平,采用正交设计表L144(67)产生144套数值模拟方案,参数水平取值见表1。

表1 正交设计参数水平取值

Tab.1 Orthogonal design parameter level value

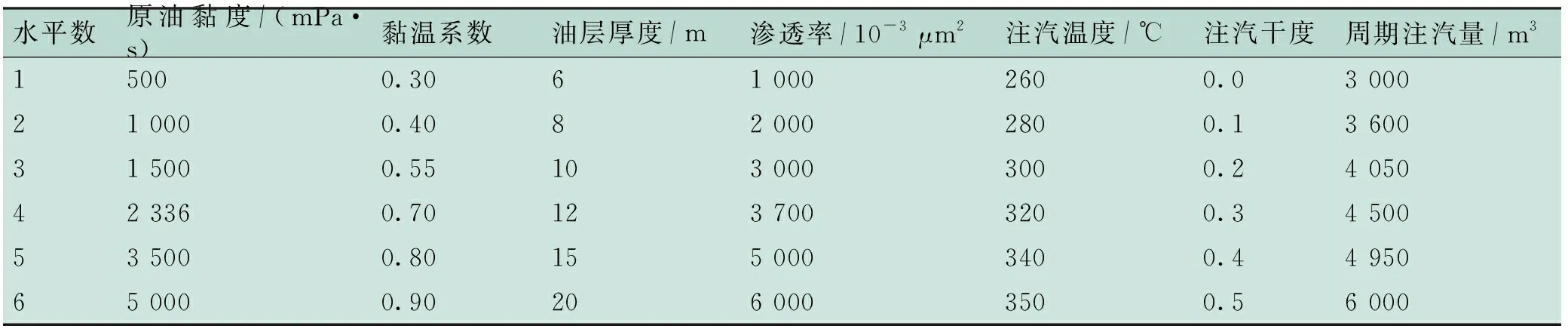
水平数原油黏度/(mPa·s)黏温系数油层厚度/m渗透率/10-3 μm2注汽温度/℃注汽干度周期注汽量/m315000.3061 0002600.03 00021 0000.4082 0002800.13 60031 5000.55103 0003000.24 05042 3360.70123 7003200.34 50053 5000.80155 0003400.44 95065 0000.90206 0003500.56 000

2.3 多元非线性模型的回归与验证

2.3.1 多元非线性回归方法选取

在建立蒸汽吞吐递减率预测模型时,需要进行递减率与上述7个主控因素的多元非线性回归。常规的多元非线性回归方法(例如BP神经网络算法),收敛速度较慢,并且很容易收敛到局部极小点[18]。本文采用Levenberg-Marquardt算法进行多元非线性回归,该算法能够克服BP神经网络的这些缺点,并且杨柳等人也证明其在某些奇异条件下仍具有很好的二阶收敛性。该算法已用于蒸汽吞吐采收率的多元非线性回归,取得了较好的拟合效果[19-20]。具体计算过程如下。

1)输入多元回归系数矩阵的起始点X(0),精度ε,k=0。

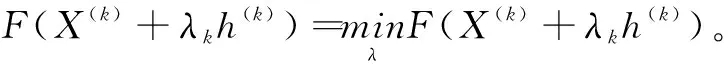
5)如果‖X(k+1)-X(k)‖<ε,得到最优解Xopt,停止计算,否则转向第6步。

7)终止计算。

2.3.2 模型回归结果

根据单因素研究得到的递减率与单因素的相关关系,采用Levenberg-Marquardt算法对132个拟合样本进行多元非线性回归,得到递减率的多因素回归公式如下:

D=-8.981 3×10-7μ2+7.898 5×10-3μ+

97.874 8e0.224 425n-11.319 9h0.320 318+

1.451 9*ln(k)+4.561 9×10-4e2.610 6×10-2T-

0.220 973q2+24.795 5q+

0.542 859*ln(W)-99.566 5

(2)

式中:D为蒸汽吞吐周期内递减率,%;μ为原油黏度,mPa·s;n为黏温系数;h为油层厚度,m;k为储层渗透率,10-3μm2;T为井底注汽温度,℃;q为井底注汽干度;W为周期注汽量,m3。

回归模型复相关系数r=0.976 3,统计参数F=5 349,设定显著性水平为α=0.01,查F(7,6)表得临界值λ=8.26。由于F=5 349>λ=8.26,所以检验效果显著,即回归模型有意义。

2.3.3 模型可靠性验证

由式(2)计算样本方案中拟合样本和检验样本的递减率,计算值与实际值的关系见图5。拟合样本最大计算误差 2.601 1 %,最小计算误差 0.044 2 %,平均计算误差为 1.159 2 %;检验样本最大计算误差 2.617 9 %,最小计算误差 0.368 9 %,平均计算误差为 1.144 6 %,多因素回归公式预测结果能够满足工程计算要求。

3 实例应用

采用蒸汽吞吐递减率预测新模型,根据黏温系数、油藏静态参数和注汽动态参数,预测了NB和LD油田蒸汽吞吐周期内递减率,计算值和实际值基本一致,证明了该模型在矿场实践中能够满足精度要求,见表2。以前热采方案设计只关注年产油和累产油指标,而不能明确周期内产量递减情况和热采有效期,给海上油田措施实施计划和后评估工作增加了难度。蒸汽吞吐递减率多元回归模型建立后,在蒸汽吞吐方案设计时就能明确蒸汽吞吐周期内递减情况,解决了这一难题。通过本文的蒸汽吞吐递减率多元回归模型,预测LD油田A 22 H井周期内递减率为26.2%,蒸汽吞吐有效期为210 d,与实际生产情况基本一致,见图6。

图5 蒸汽吞吐递减率预测模型计算可靠性验证图Fig.5 Calculation reliability verification map for the prediction model of steam stimualtion decline rate

表2 NB和LD油田蒸汽吞吐周期内递减率计算表

Tab.2 Calculation table of decreasing rate in steam stimulation cycle of NB and LD oilfields

油田原油黏度/(mPa·s)黏温系数砂体厚度/m渗透率/10-3 μm2温度/℃注汽干度周期注汽量/m3实际值/(%)计算值/(%)NB5000.383 00024003 0003.33.0LD2 3360.883 00030003 00026.626.2

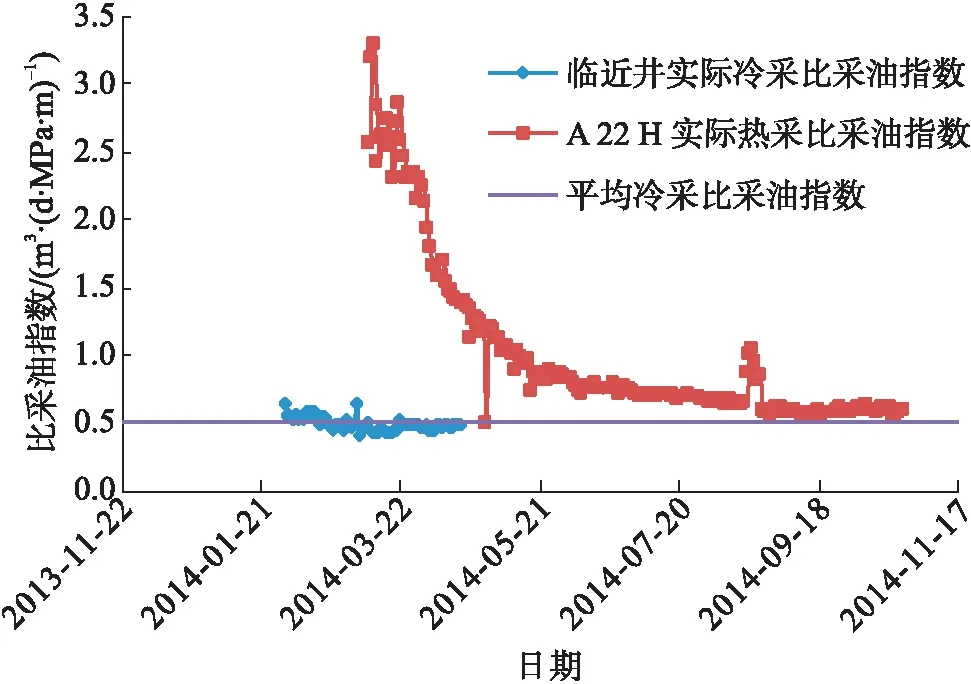
图6 LD油田A 22 H井蒸汽吞吐周期有效期分析图Fig.6 Validity period analysis of steam stimulation for A 22 H well in LD Oilfield

4 结论

1)不同胶质沥青质含量的稠油对温度敏感性不同,黏温系数与胶质沥青质含量呈较好的线性关系。因此,不同油田的蒸汽吞吐周期内递减率差异预测必须考虑黏温系数的影响。

2)针对渤海海域稠油油藏特点,通过典型区块油藏数值模拟手段,研究了蒸汽吞吐加热区的温度场和原油黏度场变化规律,黏温系数属于对产量递减规律的直接影响因素,而其它参数通过影响加热区温度场的分布范围和下降速率来影响产量递减规律。

3)在单因素影响相关关系分析和效果预测样本集生成后,采用多元非线性回归方法,建立了考虑黏温系数影响的蒸汽吞吐递减率预测新模型,计算结果和实际区块应用均表明该模型计算精度较高,能够满足稠油油藏蒸汽吞吐周期内递减率和有效期预测要求。