基于分形理论的菱镁矿粉磨程度表征研究
罗奔, 李闯*,2,3, 杨云川
1.沈阳理工大学 材料科学与工程学院,辽宁 沈阳 110159; 2. 矿物加工科学与技术国家重点试验室,北京 102628; 3. 东北大学 资源与土木工程学院,辽宁 沈阳 110004
1 引言
菱镁矿是一种碳酸镁矿物,用途十分广泛。因其中的氧化镁具有较强的耐火性、黏结性及其他优良物化特性,被广泛应用于耐火材料的制备;还可以利用菱镁矿提炼金属镁,在冶金、化工、建材及医疗等领域也发挥着巨大的作用[1]。
中国菱镁矿产量及出口量均居世界首位,是我国的优势矿产资源之一[2]。虽然我国菱镁矿储量丰富,但由于近年来采富弃贫的采集方式,使得我国优质菱镁矿资源开发殆尽,而低品位菱镁矿不能直接用于生产高级材料,因此需通过选矿来实现对低品位菱镁矿的合理利用。而在选矿过程中,选择合适的磨矿细度有助于使目的矿物与脉石矿物有效分离,对浮选过程十分有利[3]。郗悦等[4]以辽宁海城地区的菱镁矿为原料,在反浮选试验研究里指出磨矿细度在-0.074 mm含量为85%时为最佳条件;董庆国等[5]在辽宁某低品位菱镁矿浮选除杂试验研究中发现当磨矿细度在-0.074 mm含量为85%时回收率达到最大值。
但上述研究中对于菱镁矿粉磨程度的表征仍是定性分析,因为对于具有不规则形貌的颗粒破碎材料,传统欧式几何理论无法实现对其的定量描述,而分形理论作为二十世纪非线性科学研究的重要成果,可以用于解决这一问题。
分形理论在20世纪70年代由Mandelbort[6]在针对海岸线长度的阐述中首次提出,近50年来,分形理论被广泛应用于信息、数学、材料、艺术等领域,成为人们研究非线性科学的重要工具[7-10]。
自然界中的分形分为有规分形和无规分形,研究表明,破碎颗粒材料大多满足自相似,属于无规分形,颗粒粒度分布可用分形维数表征[11-13]。对于矿物破碎材料研究领域,谢和平等[14]在试验中发现分形维数可以直观地定量反映岩石破碎的程度;焦红蕾等[15]利用分形理论建立颗粒数分布模型、颗粒表面积分布模型和颗粒质量分布模型来表征煤炭研磨颗粒粒度分布。但运用分形理论来表征菱镁矿粉磨程度的研究尚未见报道。
本文以菱镁矿为原料制备不同磨矿细度的菱镁矿粉体,通过激光粒度仪测量其粒度分布,结合分形维数定义,以MATLAB软件为平台,探究如何实现菱镁矿粉磨程度的定量表征,探寻体分形维数与磨矿细度的关系。为优化低品位菱镁矿浮选结果提供一个新思路。
2 实 验
2.1 样品制备
本文选用来自辽宁省丹东地区的天然菱镁矿,其主要化学成分分析结果见表1。
表1原矿化学成分分析
Table1 Analysis of raw ore chemical composition

ComponentMgOCaOSiO2TFegrade/%45.21.093.180.34
将原料经颚式破碎机、圆锥破碎机两段破碎后过筛,按照磨矿质量浓度67%称取200 g矿样与98.5 g水混合,加入球磨机湿磨,通过调整磨矿时间,得到磨矿时间与磨矿细度的关系,如图1所示。
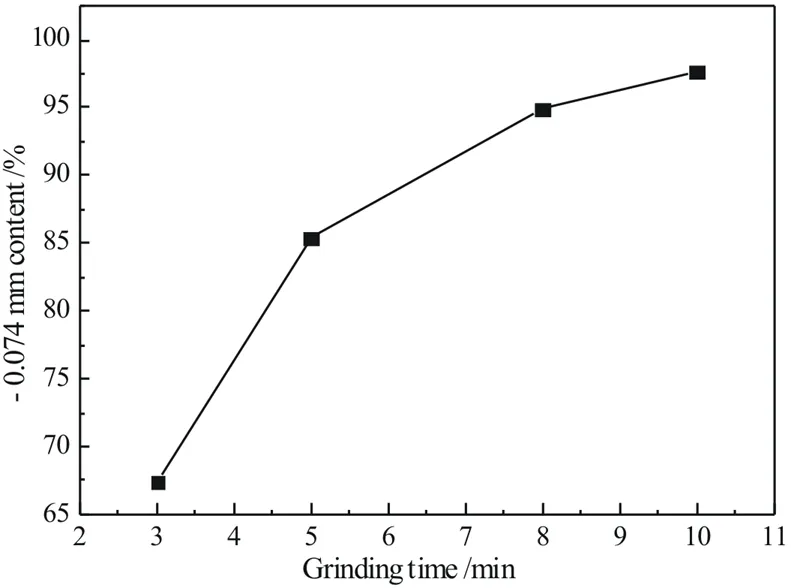
图1磨矿时间与磨矿细度关系曲线
Fig. 1 Relationship between grinding time and grinding fineness
为探寻分形维数与磨矿细度的关系,需制备不同磨矿样品,本文选取5个时间点,分别制备磨矿细度为73.8%、77.5%、81.6%、88.8%、94.2%的菱镁矿粉体各500 g,装袋备用。
2.2 粒度检测试验
利用五点取样法取制备好的矿样1 g,与100 mL去离子水配置浓度为1%的溶液,将其加入BT-9300S型激光粒度仪,超声3 min后开始测量,采用配套的软件记录测试结果,导出颗粒粒度检测报告。

图2磨矿细度试验流程图
Fig. 2 Flowsheet of grinding fineness test
2.3 不同磨矿细度的选别试验
取250 g制备好的矿样,按照2#油用量20 g/t,捕收剂十二胺用量150 g/t的试验条件,利用单槽浮选机进行除硅反浮选。磨矿细度试验流程如图2所示。
2.4 试验仪器及方法
粒度检测试验设备采用丹东百特仪器有限公司的BT-9300S型激光粒度仪,其粒径测定范围为0.1 μm~340 μm,重复性误差和准确性误差均小于1%(标样D50偏差)。首先进行参数设置,设置测试样品的介质和遮光率;然后进行背景测试,消除管道中气泡,进行光路校正,减小试验误差;将配置的溶液加入,经超声分散后进行测量,采用配套的软件记录测试结果,导出检测报告。结合分形维数定义,以MATLAB软件编程,可求出用于描述粉磨菱镁矿粒度分布特征的体分形维数和特征粒径。
3 粉磨菱镁矿粒度分布特征
3.1 粉磨菱镁矿粒度分布分形维数研究
大量研究表明,矿物破碎材料粒径分布是十分复杂的,这些粒径不一的颗粒形貌不规则、呈无序分布,使用传统欧氏几何无法实现对其的定量表征,但由于其满足分形理论的自相似性,从而可以利用分形理论探讨其粒度分布特征。
(1)体分形维数计算数学模型
Rosin-Rammler分布形式通常通过负累计率的形式表征,其数学表达式如下:
(1)
式中:y-为粒径大于x的菱镁矿质量负累积率,x为特征粒径,xe为分布模数;m为便于建立分形维数测定数学模型,以下描述选取Rosin-Rammler分布的正累积率表达形式。
本文应用Yang[17]提出的体分形维数测定方法。假设一个单位长度的特征粒径为R=xe/x,其与分形特征粒径的关系为:
(2)
式中:D3为体分形维数。
菱镁矿质量正累计率y+对于R的导数与y+成正比,与RF成反比,其微分形式为:
(3)
式中C1=kC2,对(3)式积分可得:
(4)
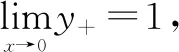
(5)

(2)体分形维数计算
根据粒度检测报告,由上述体分形维数计算数学模型,可计算出不同细度下菱镁矿样品的特征参数。计算结果见表2。
表2不同细度下菱镁矿粒度分布特征拟合结果 /%
Table2 Fitting results of particle size distribution characteristic of magnesite at different fineness fineness
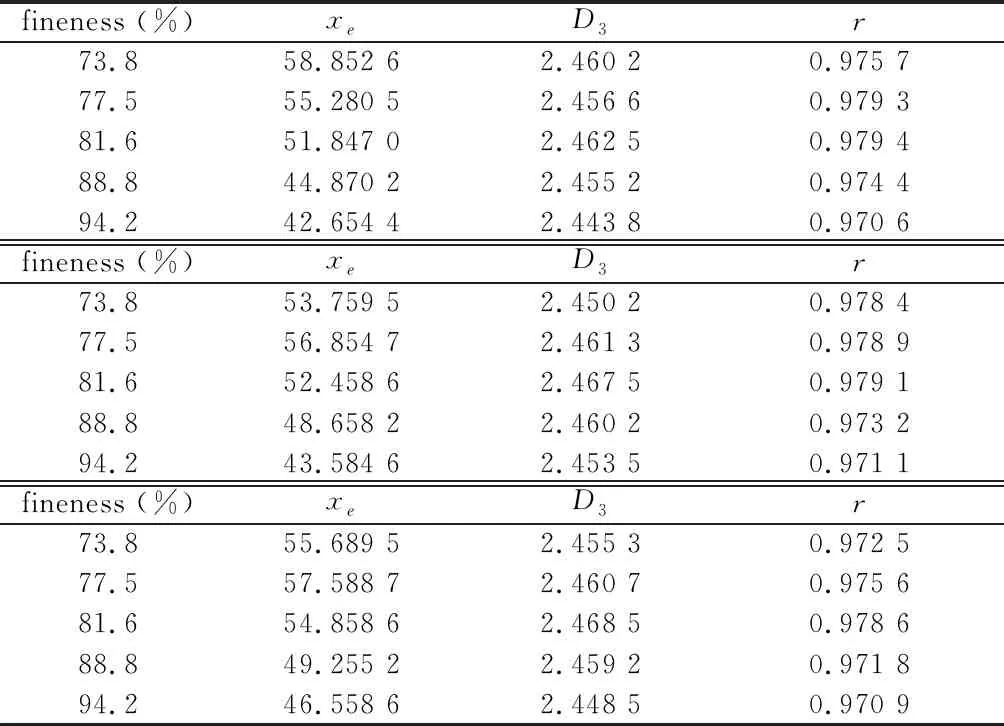
fineness (%)xeD3r73.858.852 62.460 20.975 777.555.280 52.456 60.979 381.651.847 02.462 50.979 488.844.870 22.455 20.974 494.242.654 42.443 80.970 6fineness (%)xeD3r73.853.759 52.450 20.978 477.556.854 72.461 30.978 981.652.458 62.467 50.979 188.848.658 22.460 20.973 294.243.584 62.453 50.971 1fineness (%)xeD3r73.855.689 52.455 30.972 577.557.588 72.460 70.975 681.654.858 62.468 50.978 688.849.255 22.459 20.971 894.246.558 62.448 50.970 9
图3是不同磨矿细度下菱镁矿相对质量负累计规律。可以看出,菱镁矿粒径与相对质量负累积率是一条“S”型曲线,符合Rosin-Rammler分布规律,且拟合曲线与试验曲线十分接近,只在中粒径附近存在一定的偏差,但相关系数都在97%以上;这说明粉磨菱镁矿颗粒质量分布满足统计意义上的自相似性,可以用分形维数来定量表征。
4 体分形维数与磨矿细度关系验证
4.1 磨矿细度试验结果
将浮选试验得到的精、尾矿烘干取样,经化学成分分析可得到不同磨矿细度下菱镁矿精矿产率、MgO品位、MgO回收率,结果如表3和图4所示。
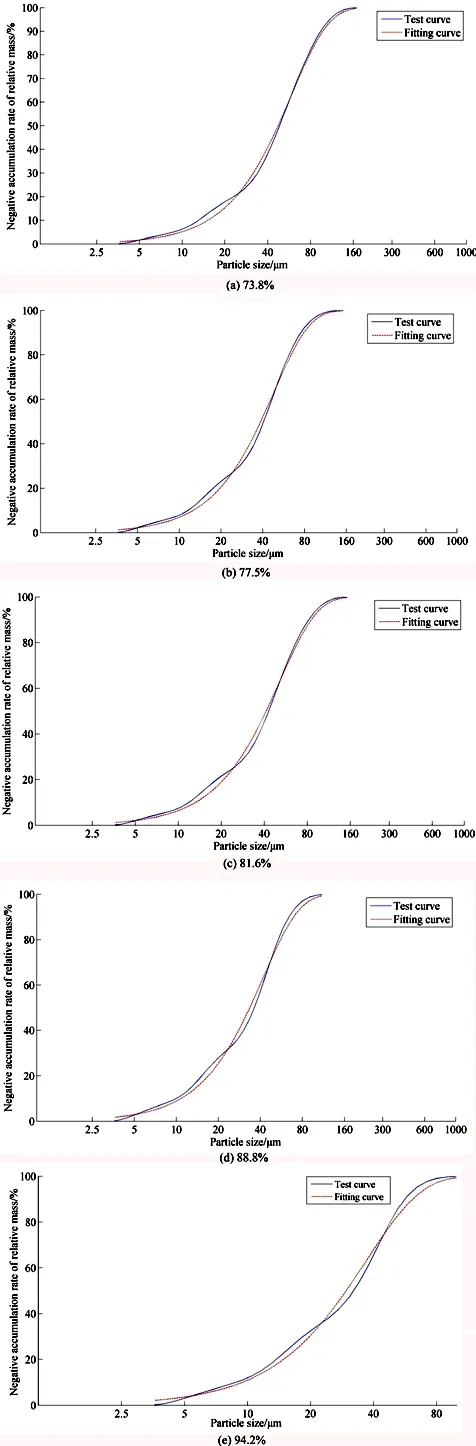
图3不同磨矿细度下菱镁矿相对质量负累积规律
Fig. 3 Negative accumulation of relative mass of magnesite at different grinding fineness
由图4可知,共进行3组选别试验,每组分别为5个不同细度,共计15次试验。发现随着磨矿细度的增加,精矿中MgO品位大体呈先增长后减小的趋势,且MgO回收率也是先升高后降低,当磨矿细度为81.6%时,MgO品位、回收率达到最高。经综合考虑,确定试验最佳菱镁矿浮选条件为磨矿细度为-0.074mm含量81.6%。
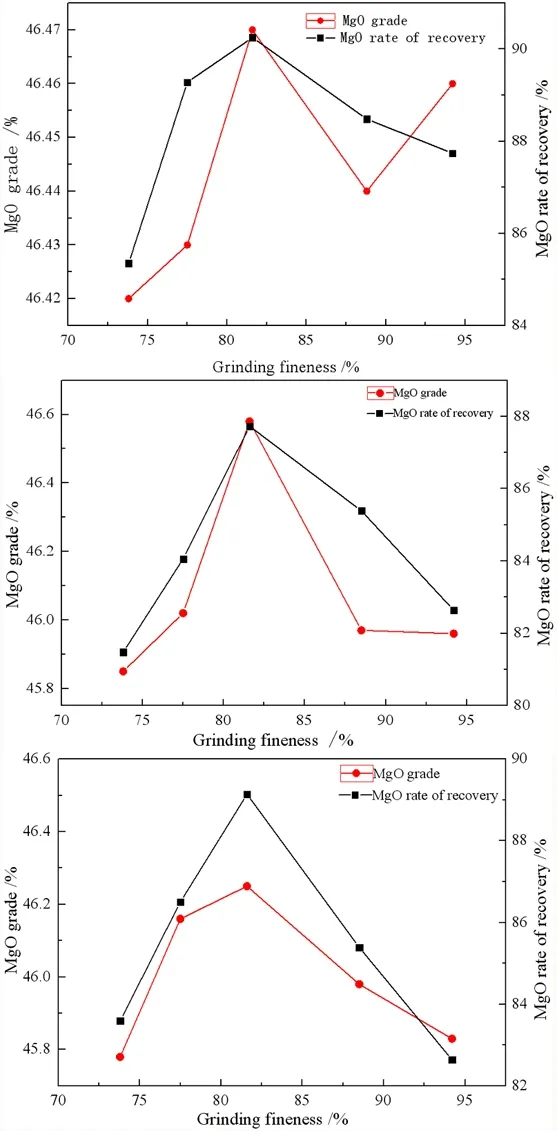
图4磨矿细度试验结果
Fig. 4 Results of grinding fineness test
表3磨矿细度试验结果
Table3 Results of grinding fineness test
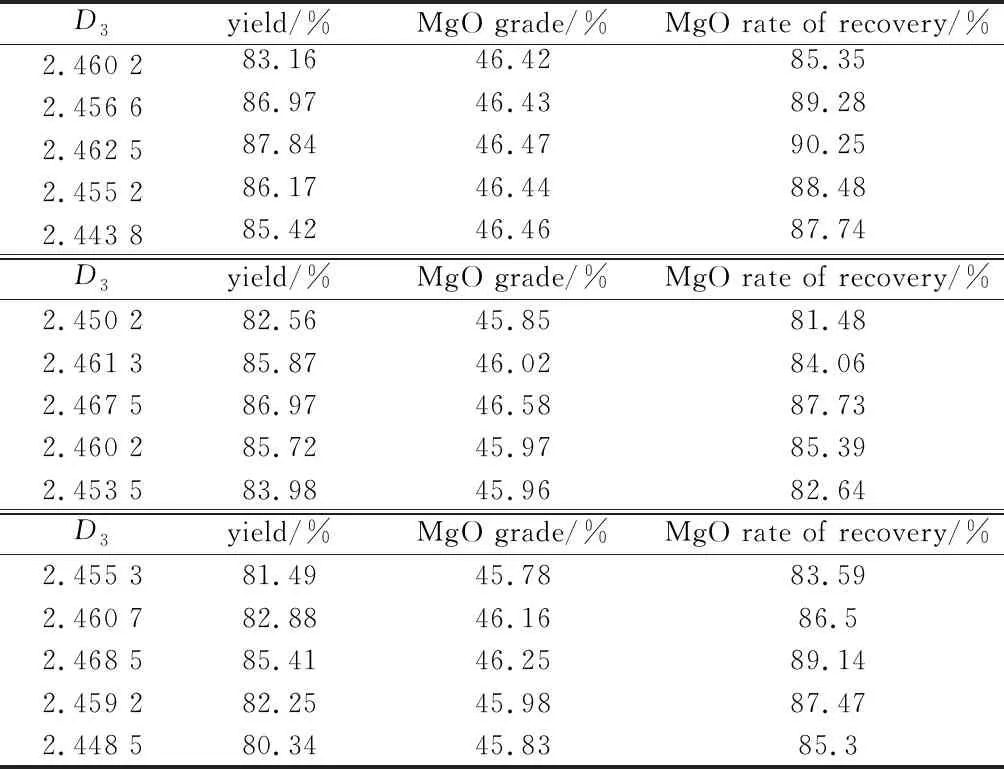
D3yield/%MgO grade/%MgO rate of recovery/%2.460 283.1646.4285.352.456 686.9746.4389.282.462 587.8446.4790.252.455 286.1746.4488.482.443 885.4246.4687.74D3yield/%MgO grade/%MgO rate of recovery/%2.450 282.5645.8581.482.461 385.8746.0284.062.467 586.9746.5887.732.460 285.7245.9785.392.453 583.9845.9682.64D3yield/%MgO grade/%MgO rate of recovery/%2.455 381.4945.7883.592.460 782.8846.1686.52.468 585.4146.2589.142.459 282.2545.9887.472.448 580.3445.8385.3
4.2 体分形维数与磨矿细度关系验证
综上所述,体分形维数与磨矿细度关系如图5所示。
由图5可知,当体分形维数最大时,所对应的磨矿细度为-0.074 mm含量81.6%。说明在3次试验中,当体分形维数处于极大值时,菱镁矿磨矿细度也为最佳条件,证明了粉磨菱镁矿的粉磨程度通过体分形维数来进行定量表征是合理的。
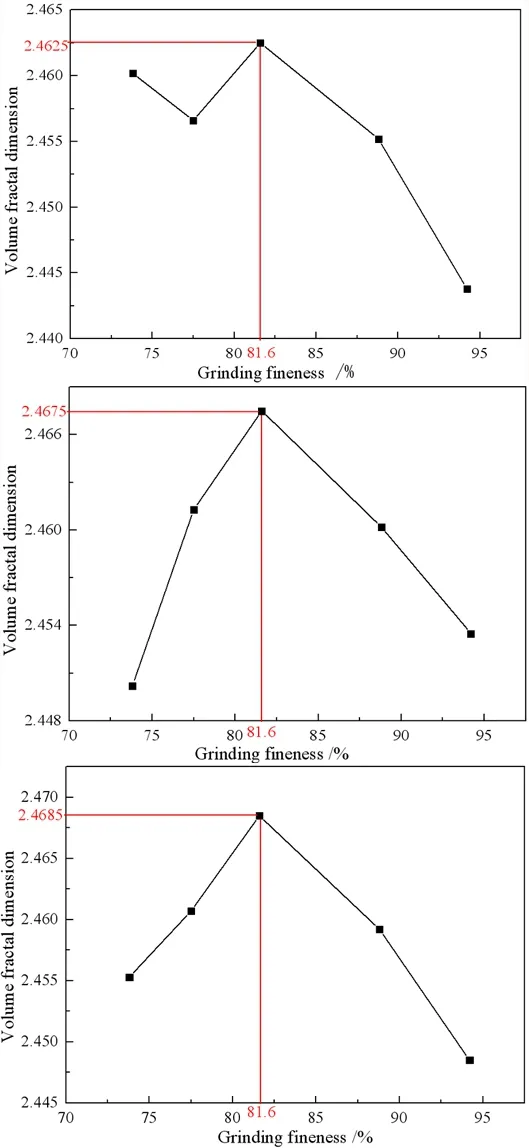
图5体分形维数与磨矿细度关系图
Fig. 5 Relationship between volume fractal dimension and grinding fineness
5 结论
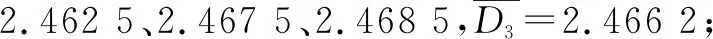
(2)本文选取5个不同磨矿细度作为变量,通过3组选别试验发现磨矿细度为-0.074 mm含量81.6%时,浮选效果较好。
(3)本文研究了体分形维数与磨矿细度关系,结果表明:当体分形维数达到极大值时,其对应的菱镁矿磨矿细度浮选效果较好,证明了菱镁矿的粉磨程度可以通过体分形维数来进行定量表征。为描述菱镁矿粉磨程度提供了一个新的表征手段,建立了体分形维数与选矿浮选的联系。

