基于凸包的电池片边缘缺陷检测算法

(1.山西大学 软件学院,太原 030001; 2.河北工程大学 信息与电气工程学院,河北 邯郸 056038;3.秦皇岛可视自动化设备有限公司，河北 秦皇岛 066007)

0 引言

随着国家对新能源开发的重视与投入，光伏发电已经成为近年来发展最快的新能源技术，目前，我国已经成为了世界上最大的光伏生产国，提供了全球90%以上的硅片供给。其中太阳能电池片是光伏发电设备的基础配件，其生产速度和每片的质量是决定光伏发电设备质量最重要的因素[1]。而随着大规模机器化生产，仅靠提高生产工艺与技术是无法实现电池片100%的良品率的，这就需要对生产的电池片进行分检。传统的分检操作由人工进行，因此效率无法保证，分检的标准也因人而异。因此，数字图像处理技术被应用到流水化生产过程中。现有设备都是通过相机获取电池片的图像，并通过对图像数据进行处理与分析，判断当前电池片存在的问题并进行分类。

目前已有的分选机主要对电池片进行的检测种类有颜色分选、表面赃物、划痕、断栅、崩边、缺角、脱晶等。其中颜色、脏污等决定了电池片的光电转换性能，而崩边、缺角等决定了电池片的生产质量。因此，在工业生产分检过程中，优先保证产品质量，淘汰存在缺陷的电池片，进而根据颜色等其他标准将电池片按性能等级来分类。这就要求在自动化检测过程中，首先检测电池片的边缘缺陷，这一检测不仅要求判断的准确率高，还要求具有极快的处理速度[2]。

边缘缺陷检测在数字图像处理中一直有着广泛的研究并在工艺零件探伤，生产质量监控中有着重要应用。近来，钱基德等人[3]针对高分辨率的大型液晶屏采集图像进行处理，提出改进的梯度优化方法来快速、准确的检测液晶屏边缘不亮的产品。而蒋莉等人[4]也提出了基于形态学的方法来检测液晶屏生产过程中的边缘不亮的不良品。另外，刘建春等人[5]通过合理使用现有的膨胀腐蚀等数字图像处理方法对高光垂直照射下的零件边缘的细小缺陷进行了识别与检测。如何对已有理论方法进行优化、改进，进而将其应用到工业生产中，实现快速、准确地完成识别任务已经成为了目前的研究热点。

针对太阳能电池片的边缘缺陷检测方法也一直在研究，但并没有可以直接应用到分选机上的合适的算法。姚明海等人[6]提出了基于RPCA(robust principal component analysis)的太阳能电池片表面缺陷检测方法，该方法实现并优化了已有的逼近梯度算法和非精确增广拉格朗日乘子算法。但是，这两种算法在进行电池片检测时，需要使用16幅像素为830*586电池片图像组合成为一张图像进行处理，这种预处理的过程与实际工业生产过程不符，难以应用。同时，处理过程中大量的迭代计算也使得每幅图检测的最短耗时达到2.21 s。Fu[7]则提出以电池片颜色分布梯度为标准进行缺陷检测，然而这种检测方法对背景灰度分布的依赖性高，且边缘位置本身具有高梯度值，所以无法准确处理边缘位置的缺陷。

随着人工智能技术的发展，研究人员也试图通过深度学习与神经网络等技术实现电池片边缘的缺陷检测。王宪保等人[8]提出了基于深度学习的缺陷检测方法，该方法将像素为64*64的图像作为训练对象，平均每张图片检测消耗0.151 s。但是该方法在针对工业中使用的千万像素级别的图像建立训练集时困难极大，同时对于像素较大的图像，找到缺陷位置并训练也难以实现。伍李春等人[9]针对上述难题提出了利用模板匹配及颜色直方图匹配的方法，优先通过匹配识别找到疑似缺陷的位置，之后再进行训练。该方法仅将可以检测的图片尺寸增大到了656*492像素。刘磊等人[10]则提出了在经过新的预处理方法之后进行学习分类的方法，该方法已经可以训练千万像素的图像，但由于预处理方法简单，识别准确度不高。

无论是传统的数字图像处理方法还是加入机器学习的新方法，都需要一种稳定、快速且准确的判断边缘缺陷的方法。而现有的边缘检测算法通常默认图像中电池片边缘是一条直线。这并不符合实际生产中采集得到的图像，因此使得已有算法在应用中往往出现大量误判。同时，随着分选机检测项目的增多和检测精度要求的提升，如何降低单项检测的处理时间，提高单项检测的处理结果的复用成为了迫切需要解决的问题。因此，针对电池片本身的形状特征，提出一种基于凸包的快速边缘缺陷检测算法。该算法结构流程如图1所示，其通过对电池片边缘点集进行凸包运算，进而获得缺陷点集中每个点的缺陷深度。同时，还能计算出电池片几何中心点以及电池片的偏转角度，便于传输归正和其他缺陷检测过程复用。实验证明，该算法较已有算法在速率上大幅提升，且在实际生产中的检测过程中表现良好，检测效果达到了分选机的工业生产标准。

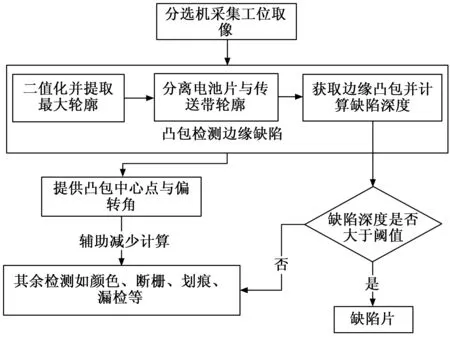
图1 凸包检查边缘缺陷结构功能图

1 电池片边缘检测

1.1 图像获取与分析

太阳能电池片的缺陷检测多用于如分选系统，串检系统等流水线类型的检测机器上，而电池片的拍摄方法都是由检测系统的视觉工位完成。在分选机的视觉工位中，一般通过置于顶部的相机向下方拍摄，电池片在下方通过传输带运送，整个拍摄环境在球形或立方形的暗室中进行。因此获取的图像中一般存在电池片主体，传输皮带(部分分选机结构不使用皮带传输)以及传输过程中产生的碎片等杂质。这里以实际生产使用中的一台分选机获取的图像(如图2)为研究对象。

因电池片边缘缺陷极小，而工业生产中对一张160 mm边长的电池片的检测精度至少要达到0.1 mm。假设像素距离与物理距离的比值K值为0.1 mm/pixel，则至少需要电池片占满一张1 600×1 600像素的图像才能拍摄出电池片边缘达到0.1 mm以上的缺损信息。该算法所使用图像为千万级像素相机所拍摄的三通道24位彩色图像，其分辨率为3 440×3 324像素，电池片占据图像2/3以上部分，因而可以保证K值小于0.1 mm/pixel。用A4纸,页边距上下左右已经设置好,请不要改动。

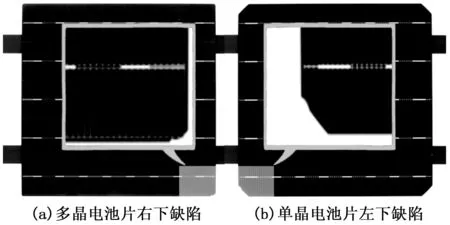
图2 单晶与多晶电池片轻微破片正面图像

图2中分别为具有边缘缺损的多晶电池片和单晶电池片的图像，其中图2(a)为多晶电池片，其缺陷在图中右下角，而图2(b)为单晶电池片，其缺损在左下角。不难发现，图片中的缺陷极小，难以观察，同时由于图像像素规模大，传统的边缘缺陷检测方法需要大量时间寻找缺陷位置并计算深度。图2中的图像是从具有立方体暗室的分选机上拍摄得到，图像中的传输带影响了在传输带上方电池片边缘的检测过程(即便使用白色或透明传送带，也会因长时间使用而变脏污影响检测)。另外，为了使得电池片边缘与背景易于区分，电池片下方存在白色背光源打亮背景，因而导致部分边缘信息丢失进而影响边缘缺陷检测。此外，由于传输结构的稳定性不足，每次拍照时电池片位置与角度存在偏差，因此每张图像中的电池片会因透视效应和镜头畸变而导致尺寸仅存在差异，且电池片边缘非直线，进而影响边缘缺陷的检测过程。

为此，针对图像中缺陷深度过小，背景脏污干扰以及电池片形状畸变等问题，提出一种基于凸包的边缘缺陷检测算法。该算法在成像结果中电池片形状存在畸变的情况下，依然可以准确稳定地获得缺陷位置与深度。该算法包含三步：首先，利用传统的阈值分割将前景与背景分离；其次，获取前景图像的边缘轮廓点集；最后，计算轮廓点的凸包并得到凹陷位置和凹陷深度。

1.2 电池片边缘点集提取

从图2中所示的电池片缺陷图像可知，图像中的电池片本身及传输带与白色背景易于区分，电池片边缘线清晰可识别。同时，电池片上纹理信息(即电池片表面栅线)并未绘制到电池片边缘，可见电池片边缘与背景交线的两侧颜色单一，易于提取。因此，该算法首先对图片进行阈值分割得到二值化图像，进而突出电池片边缘，分离背景与前景信息。

实际生产中对流水线上的电池片进行取像时，由于相机安装位置与角度的固定性，所拍摄的图像中电池片的尺寸、光照基本相同，特别是对于同批次的电池片而言。因此，该算法统计多张同批次电池片图像中前景信息所占的像素比例，得到一组像素比例的样本值，计算这组样本值的均值与方差，并根据方差不断排除异常值得到稳定的平均值。以这一均值作为传统的p-分位数法[11]的先验参数，对新拍摄得到的每张图像进行阈值分割，即可快速准确地将前景与背景分离，得到保留边缘信息的二值化图像，该边缘信息包括电池片边缘与电池片下方的传输带边缘，如图3(a)所示。

图3 电池片二值化及轮廓提取效果图

自动阈值分割算法首先根据已有的大量样本文件统计出一组前景与背景的像素比例集Ti作为输入信息，通过不断加入新样本后删除这组样本Ti中的异常值点(即样本值中与均值距离最远的值)不断更新样本标准方差，直到样本标准方差值小于约定值δ，如算法1中步骤d)～k)所示，其循环过程中集合T的总容量始终小于初始样本大小。此时得到的均值mk即可作为对图像进行阈值分割的参数。在流水线检测过程中，该值会被不断更新修正，以适应传输过程中电池片之间的差异性。一般不要超过两行。

算法1:自动阈值更新算法

输入：先验参数mk所对应的样本集合T。

输出：更新后的样本集合T与其均值mk。

a) newk = Thread(img) with mk; //使用mk对图像进行阈值分割

b) T.push(newk); //将新的比例值加入集合K

c) do{

d) mk = mean(T) //计算新集合的均值

e) md = std(T) //计算新集合的标准差

f) maxk = 0

g) for i from 0 to sizeof(T) step 1

h) if(maxk < |T[i]-mk|)

i) maxk = |T[i]-mk|

j) plc = i

k) T.pop(T[plc])

l) while(md>δ)

在分选机上进行算法验证时，为了尽可能地保持检测的稳定性与准确率，在抽取相同批次的电池片样片进行预先的阈值更新算法得到分割阈值(算法1中的mk)后，使用算法1边检测边更新阈值。而在实际生产过程中，为了加快检测速度，提高检测效率，通常对同一批次的电池片使用预先计算好的阈值作为固定阈值，或采用随机选片的方式进行算法1的阈值更新过程来降低检测的运算时间。根据获得的自动阈值将图2(a)所示电池片进行二值化分割后的图像如图3(a)所示。

从图3(a)中可以看出，阈值分割后图中可能存在多个轮廓信息，包括表面纹理产生的不完整孔洞，以及传输过程中掉落的碎片引起的黑色斑点等。而利用文献[12]中提出的轮廓跟踪提取方法，可以得到图像中包括碎片等杂质的轮廓以及电池片上电极纹理等在内的所有轮廓信息。显然，在所有轮廓中电池片与传输带的轮廓是其中面积最大的一个(如图3(b)中方框内点状轮廓线所示)。而从图3(b)中的局部放大图中可以看到文献[12]中的方法所得到的轮廓是一组有序的离散点集M。图中的该点集M中还包括了电池片下方传输带的轮廓信息。此时，传输带部分的轮廓信息干扰了电池片边缘的检测，使得传输带上的电池片轮廓部分无法直接进行提取。因此，提出传输带部分与非传输带部分两种不同的检测方法，该方法需要将边缘轮廓点集M分割成电池片上部分和轮廓上部分。对电池片上部分直接使用基于凸包的边缘检测方法进行缺陷检测，而传输带上部分则通过颜色距离的方法进行检测(见2.2节)。

算法2:边缘点滤波算法

输入：轮廓上的有序点集M。

输出：电池片上的非光滑点集Q，与传输带交点集合G。

a) start = M[0]; pass = M[1];

b) for i from 2 to sizeof(M) step 1

c) dis = distance(start,M[i]);

d) ang = arcos(start,pass,M[i]);

e) if dis < least || (π-ang) near 0 /*不相邻两点间距离小于给定值或三点几乎构成直线*/

f) pass = M[i]; continue;

g) if thread < ang < π //三点构成转折线

h) Q = start //点start放入集合Q

i) if 0 < ang < thread //角度为直角，传输带转折处

j) G = pass //点pass放入集合G

k) start = pass; pass = M[i];

l) clear(G) //根据位置信息过滤错误交界点

m) for i from 0 to sizeof(Q) step 1

n) erase Q[i] between pair(G) //删除每对交界点间的点

另外，从图3(b)的局部放大图上可以看出，由于拍摄得到的电池片边缘存在相机拍摄引起的锯齿形状，导致了光滑连续的边缘上产生了大量相邻的轮廓点信息。为了保证检测精度的同时最大程度地加快后续处理的运算速度，就需要减少边缘轮廓点集M上的非关键点的信息(特别是无破损边缘上的轮廓点以及传输带上的轮廓点)。为此提出了一种边缘点滤波算法(如算法2所示)，该算法通过一次遍历电池片轮廓的有序点集M，利用三角形余弦定理进行累加计算(算法2中步骤d)，删除轮廓点集M中的大量平滑连续点(算法2中步骤m，n)，保留轮廓点中的转折点。同时，结合传输带与电池片近似直角的固有特征，得到传输带与电池片之间交点的集合G(如图4(a)中连接处点所示)，进而区分电池片的轮廓点集与传输带上的点集部分。

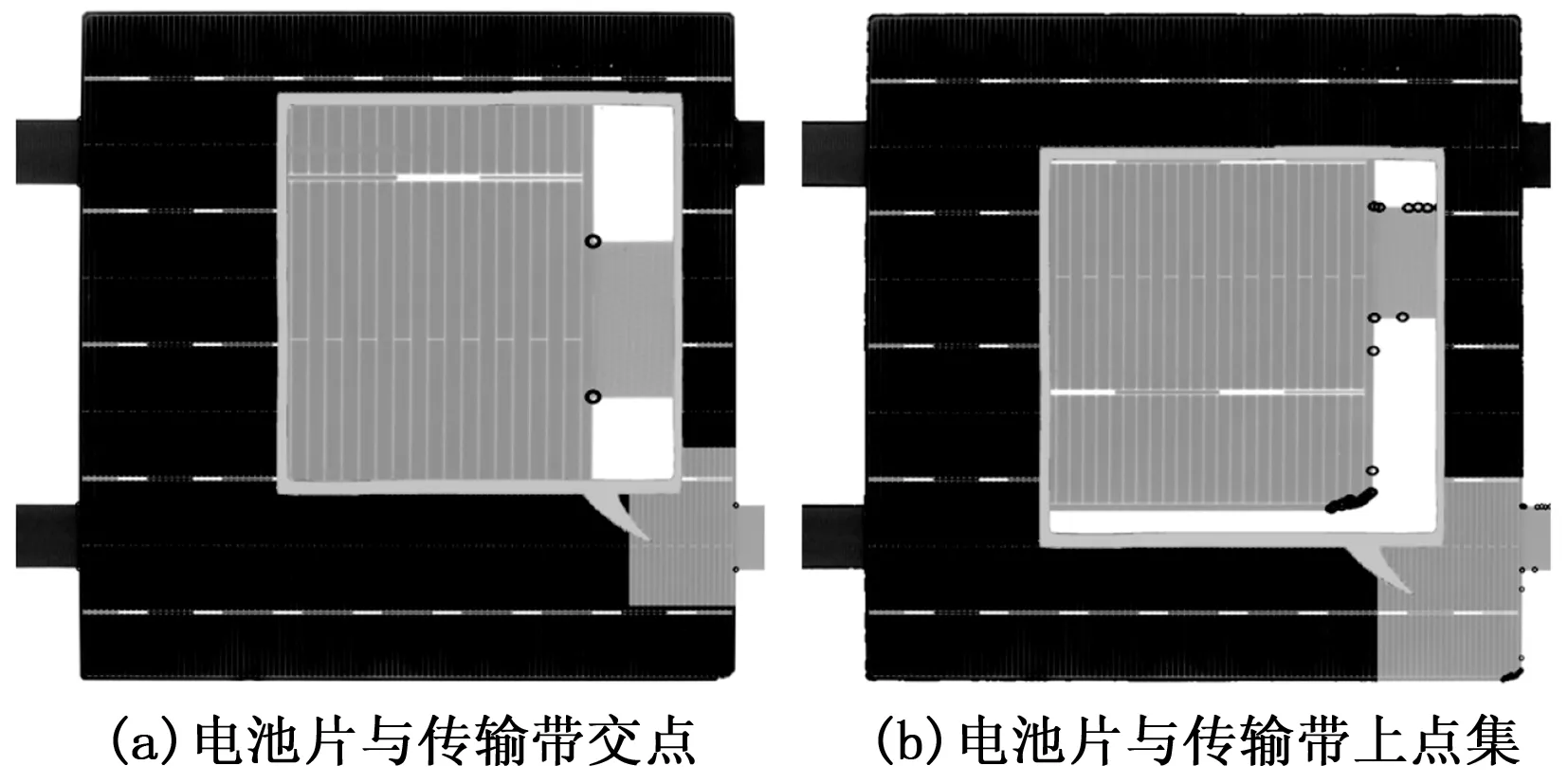
图4 电池片传输带交界点集与电池片边缘点集

1.3 边缘凸包与破片区域点集

经过算法2的滤波作用后，边缘点集被分为传输带上点集(图4(b)中传输带上点)与电池片边缘的点集Q(图4(b)中电池片角落上点)。由于电池片本身作为凸多边形的特性(即便受镜头畸变等因素影响，其所成图像中的电池片轮廓依然能够保持着凸的性质)。因此，只要对边缘点集Q进行凸包运算，得到的凸包信息就是电池片的理想完整边缘。进而根据点集Q中在凸包内、外侧点到凸包边缘的像素距离即可得到破损位置以及破损深度，其检测精度可以达到像素级别。同时，由于算法2的滤波作用，因此点集Q中需要进行的运算大幅降低，提高了检测效率。

电池片边缘点集的凸包的计算使用Jarvis步进法，由于边缘点集Q为有序点集，因此可以得到一个依然有序的凸包集合A(如图5中边线上的浅灰色点所示)和一个非凸包上点的集合B(如图5中深灰色点所示)。依次遍历集合B，得到集合A中距离集合B中元素m最近的两个点{(m1,m2)|m1,m2∈A}的坐标，最终根据这3个点的像素坐标，计算出缺陷集合B中的每个点m处的缺陷深度dm。由于得到的缺陷深度的单位为像素，因此根据2.1节中提出的比例关系K值，可知实际缺陷深度近似等于dm/10 mm。最后根据生产要求，设定筛选标准值ε，挑选出dm/10>ε的不合格品，标记显示不合格产品的缺陷位置，并给出各个缺陷的破损深度值。

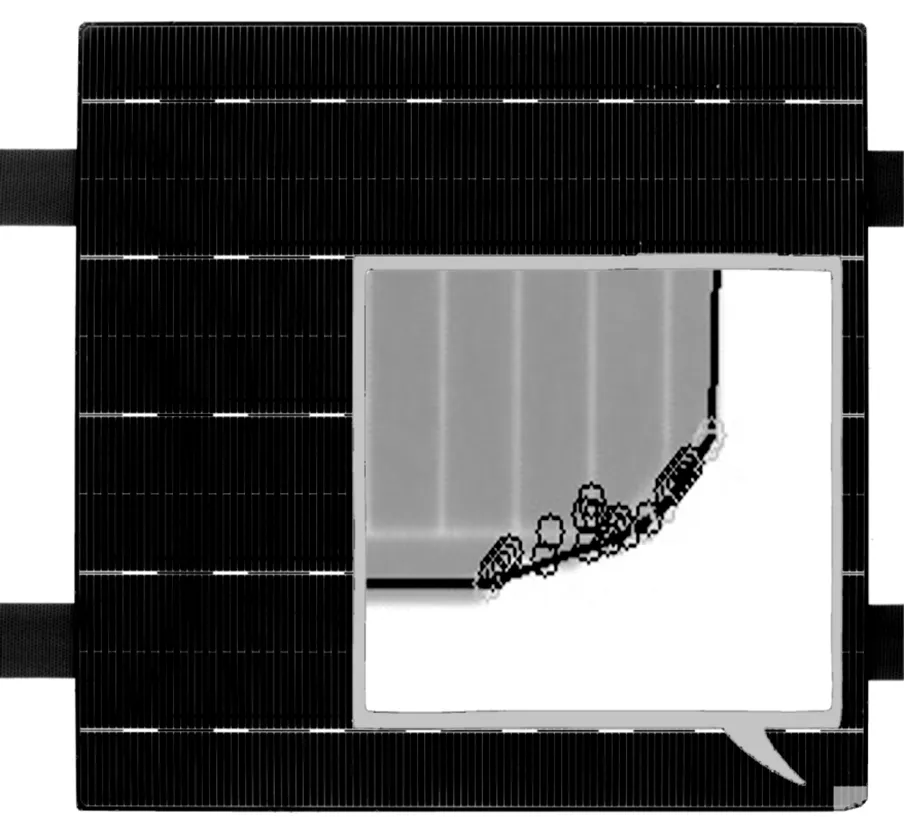
图5 电池片凸包上点集与凸包外点集

2 电池片姿态及传输带上缺陷检测

2.1 电池片姿态矫正

电池片的传输姿态对于检测正确率以及传输下料等有着重要意义，而在1.3节计算缺陷深度时得到的点集A可以很好的描述电池片的姿态信息。通过算法2得到的电池片凸包点集中的点均在电池片边缘上，且凸包构成的轮廓紧紧包裹在电池片周围。因此，凸包的重心和偏转角度就是电池片的重心与偏转角度。由于电池片的物理形状为中心对称的多变形，所以在没有较大缺损的情况下，电池片的中心即为电池片的重心。

凸包的重心可以通过将凸多边形分解为多个依次相连的三角形，之后对每个三角形的重心进行积分获得凸包的重心。若设凸包内任意一个三角形的重心坐标为(x,y)，该三角形的面积为ρ，那么二维平面内凸包的重心即为：

(1)

其中，三角形的构造可以在该获取凸包点集的同时获得。具体方法是在进行Jarvis步进法时，每找到一个新的属于凸包的点，就用该点与凸包的起点与上一个找到的凸包上的点构造一个三角形并计算其重心坐标与面积。当凸包查找完成时，构造的三角形刚好组成整个凸包。最终，在计算电池片边缘凸包的同时，也得到了凸包的重心，即电池片中心的像素坐标，减少了运算时间。计算过程如图6所示。

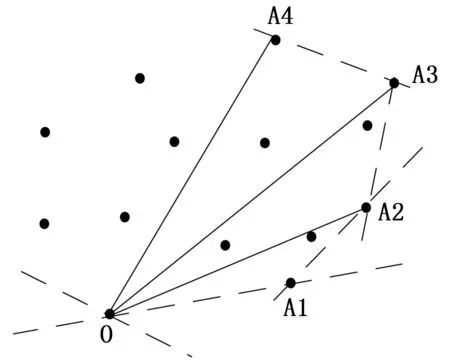
图6 Jarvis步进法求凸包及三角形分割

由算法2得到的凸包集合A中的点是有序的，结合图6所示，通过一次遍历不断计算集合内连续三点所构成的三角形，不但可以计算出电池片的重心，还可以将凸包上的点集划分成多条边线上的点集。任取其中一条边上的点集进行直线拟合，就可以得到这条边的偏转角度。而电池片自身物理形状为一个规则的多边形，因此根据边线的偏转角度的均值即可以算出电池片的偏转角度。

在生产应用中，为了加快运算速度，可以直接使用算法2得到的传输带与电池片的交点集合G来计算电池片在图像中左右两条边的偏转角度。由于存在相机安装位置以及图像畸变等因素的影响，一般选取两条边偏转角度的均值作为电池片的偏转角度。

2.2 传输带上的破片检测

当电池片的缺损位置刚好在传输带上方时，由于传输带的遮挡，无法直接通过轮廓信息得到该处的缺损信息，因此选择通过电池片与传输带之间存在颜色差异来识别边缘缺陷。通过算法2得到的交点集G中的4组交点，获取对应的四条传输带与电池片的交线段，进而判断垂直于该线段的左右像素点(片外侧点a,片内侧点b)间的颜色距离dis，用以判别交线段两侧是否存在缺陷。其中：

(2)

由于HSV色彩空间的锥形结构更适合相近颜色的距离计算，因此距离公式选用HSV分量进行计算。在实际生产中，长期使用的传输带因存在脏污而使拍摄到的传送带上存在黑色或其他颜色的使用痕迹。为此，设计了双距离检测方法，即既要计算交线段两端像素点的颜色距离，还要计算交线段两端像素点与黑色和白色的距离均值。若两像素点间的颜色距离很小或与黑色与白色的距离均值的差值很小，则称这两个像素点颜色相同，即表示两个像素点同在传输带上或同在电池片上。根据这一原则，依次判断交线段两端的像素点，若两点颜色相同，则交线短两侧可能存在缺陷，需要继续计算沿垂直于交线方向上的电池片一侧的相邻像素点，直到找到颜色距离大于设定值的像素点，该像素点到交线的像素距离就是电池片的破损深度。图7中所示为图像中所有像素点到电池片边缘上蓝色像素点的距离梯度图和图像中每个像素点到黑白像素的颜色距离均值梯度图。显然，两幅图中都可以清晰区分电池片上被传输带遮挡的边缘信息。

图7 电池片与传输带间颜色距离

3 实验与结论

为了验证算法在运算效率上的优势，选取文献中多种缺陷检测方法进行对比实验。并通过本文算法在实际生产中检测结果进行统计，验证算法的可行性与稳定性。实验环境选择在电池片分选机上搭载Win7系统的工控机中进行。实验图片通过电池片分选机上的1 500万像素的工业相机采集的高清图像，每张图片都是3 456*3 162的像素大小。程序使用Opencv函数方法，对具有不同边缘缺陷的电池片进行检测后的效果如图8所示。

由图8可知，本文算法可以检测不同类型电池片的边缘缺损情况(图中圆圈标记缺损位置)并能给出缺损深度和电池片的偏转角度(图中竖线表示当前方向，图中文字显示缺陷深度以及电池片重心和偏转角度)；当电池片上的崩边与漏浆缺陷达到边缘位置时，也可以通过该算法进行检测。此外，本文算法通过电池片正面或背面照片，甚至对破片、碎片均可正常检测，具有良好的鲁棒性。为了更好的证明本文算法的优点，选取参考文献中提到的几种主流算法及每种算法的描述与测试数据绘制对比结果如表1所示。

由表1可知，文献[6]中基于RPCA的方法检测图像尺寸较小，但时间消耗巨大，尽管可以检测出多项电池片表面的缺陷，但难以直接用于有产量要求的分选机中；而如文献[8]和[9]中基于深度学习的检测方法对训练样本的需求量较大，训练过程对运算设备的要求较高，因此大多使用小尺寸图片进行模型训练，远小于实际尺寸。而且基于深度学习的方法仅能对电池片是否存在缺陷进行分类，无法给出具体的缺陷尺寸等数据；文献[13]中仅

对电池片姿态的计算开销就远大于本文算法。本文算法的时间复杂度为O(n)级别，对较大尺寸图像依然具有很快的处理速度。因此，本文算法更适合用于进行实时检测的在线分选机设备，该算法具有运算速度快，检测精度高，能获得缺陷深度信息和电池片的位置与偏转角度信息的优点。

为了进一步验证本文算法在实际生产过程中的优越性能，选取某车间的一台分选机应用本文算法，由现场人工统计其在不同时段对不同种类电池片进行边缘缺陷检测的结果，如表2所示。其中，正检率 = 正检数 / 破损片总数(正检数+漏检数)；误检率 = 误检数 / 检测总数。

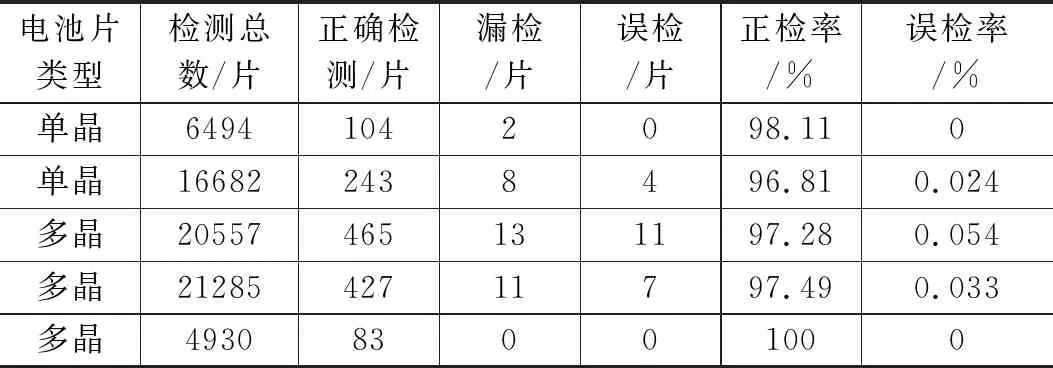
表2 全天不同时段检测结果统计

由表2可知，不管是对于颜色和形状较为稳定的单晶硅太阳能电池片，还是良品率较低的多晶硅电池片，总的正确检出率可以保持在97%以上，而误检率控制在了0.1%以下，满足电池片分选的工业生产要求。本文还选取厂区内两台不同厂家的分选机与搭载本文算法的分选机进行崩边与缺角这一单一项目的检测。由工人选取1 000张多晶电池片，其中包含20张做了标记的残缺电池片，分别使用不同的分选机对这1 000张电池片进行检测，检测结果如图9所示。

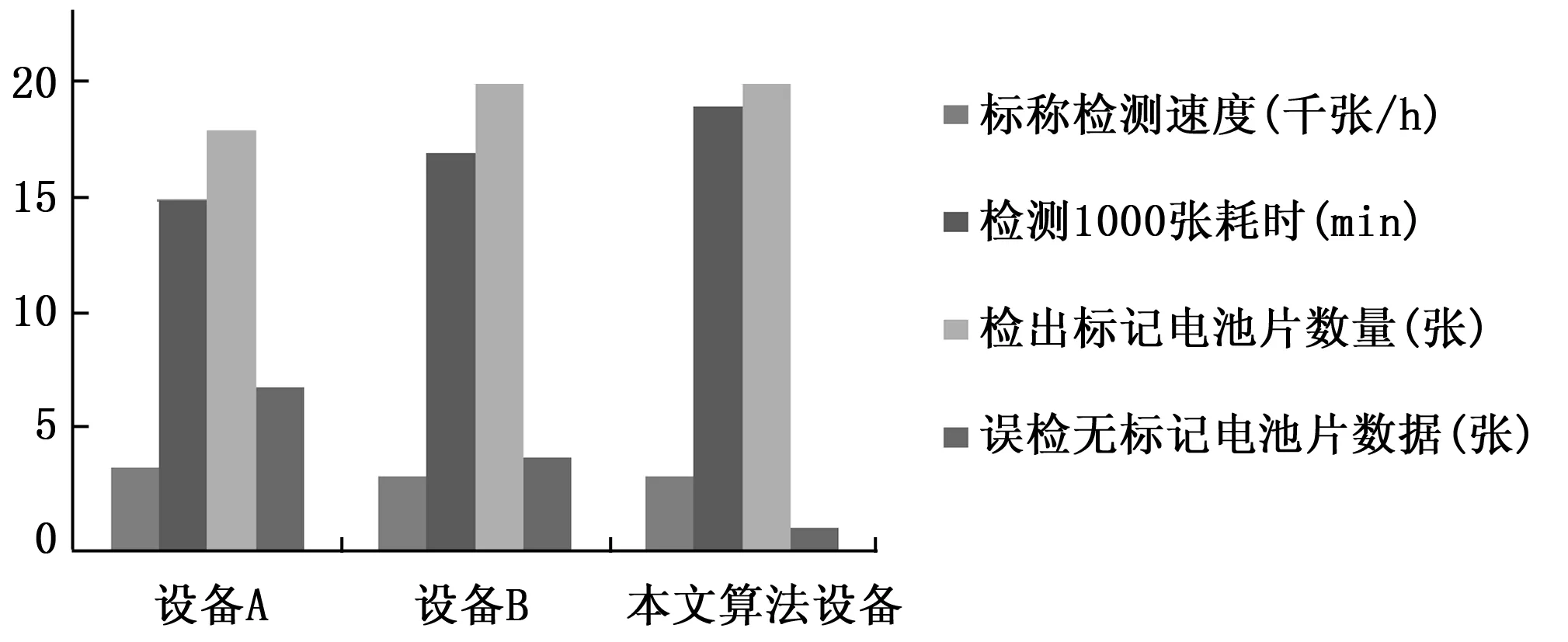
图9 3种不同分选机检测结果统计图

图9中所示3种设备都达到了标称的检测速度，该检测速度还与机械结构相关。通过对比可知本文算法检测出全部标记缺陷电池片且仅错检了一张正常片，较另外两台设备具有更好的效果和正确率。

4 结束语

综上，本文的算法在保证了电池片缺陷检测准确性的前提下，提升了检测的速度，同时算法的鲁棒性使其可以应用在不同的成像环境中，降低了设备的依赖性。与目前主流的算法相比，本文算法更适应于工业生产设备对实时性和准确性的要求。目前，算法在电池片工艺点干扰下仍会出现误判，将继续对此进行研究。