一种隧道基坑多维度时变预测EPS模型的应用

(广西有色勘察设计研究院,南宁 530031)

0 引言

众所周知，隧道工程施工过程中的基坑形变可能会造成无法弥补的伤亡事故，所以探讨一种基坑形变预测方法就变得异常重要。据统计一般的预测基坑形变的算法有：粒子群优化(PSO)算法，其特性表现在运算速度快、通用性强等特点，但不能用于深层开挖，对非线性监测差等；而神经网络预测模型，监测数据的误差过大而出现结果的不准确的弊端；而经验模式分解法(EMD, empirical mode decomposition)，能运用在复杂环境下的非稳态降噪而获得形变信号，并对所收集到含有众多信息成分的物理意义函数信号进行筛选分解，最终进行各尺度时序空间演算得出规律性的信息进而预测[1]，然而其监测精度也存在不尽人意；再者是单隐层前馈神经网络的SLFNs学习算法是一种适用于单隐层前馈神经网络的高效学习方法，它不需要多次迭代，只需要设置隐藏层数即可，但单独使用效果不佳[2]。因此，针对目前隧道施工过程中出现的时变情况下，不明原因所产生的非线性形变的预测，而且预测的精度要达到进一步提升。据此笔者提出基于信号分析法，即综合经验模态分解法EMD、和单隐层前馈神经网络SLFNs学习算法组合成的一种深隧道工程基坑多维度时变预测模型(简称EPS模型)。该算法从多维度对动态形变能形监测数据的时间序列分解为多个具有物理意义的IMF分量，采用多维耦合对相位空间进行了重构，确保预测精度。最终经实例运作，表明其具有时变提取，高精度，收敛快，适用性强等优点。

1 模型原理与方法

1.1 经验模态分解法

对于一个非平滑信号分析处理方面的研究，文献[3-4]在1998年曾经提出过作为模态分解(EMD，empirical mode decomposition)和连续均值滤波法，将EMD原始值进行分解成不同维度的趋势，同时载入原生模态函数(IMF)标准使不同的趋势作处理，EMD算法由非平滑变化的信号转为降噪，对信号分流出多个维度的本征模IMF数值[5-6]。如果原始信号数据中的x(t)上下0点处高于其极大值或极小值个数少于2或2以上，则应利用EMD算法对原始信号数值可以进一步降噪，并对其结果后的原始信号值再进一步运算筛选，从而得出多个维度函数的本征模IMF及一个残差分量R，通过对比分析原始数值与不同时间维度上排序变化就能得到时变的信号源。该模态的演算步骤如下：

1)设为始值为时间变化序列x(t)，先进行对信号源值求出所有极值点，用3条曲线函数拟合极值点的包络曲线，再进行方程式运算得到其均值，即为:

m1(t),则原始序列x(t)和m1(t)的差值为第一个分量，记作h1(t):

h1(t)=x(t)-m1(t)

(1)

2)当h1(t)吻合本征模IMF数值时，则h1(t)也会成为首个与本征模IMF数值分量契合的函数，否则将会作为原数据再进入上式，即成为：

h1(t)=h1(t)-m1(t)

(2)

3)重复进行以上筛选步骤k次，直到h1k(t)满足IMF条件为止。令h1(k)(t)=c1(t)=c1(t),则c1(t)为包含原始数据最优的第1阶IMF函数分量。

4)将c1(t)从原始数据x(t)中分开得:

r1(t)=x(t)-c1(t)

(3)

式中，r1(t)代表残差分量R值，通过将其迭代成为一个新的源值，并重复上面的运算，得出x(t)的第二阶段本征模IMF数值，就是这样的多次运算下n个周期内，求出原始序列x(t)，如式(4)。

n个IMF分量，其表达式为:

(4)

5)若rn(t)在重复的运算过程下不能再有新的本征模IMF数值被分解出来时，运算就会终止，从而获得最末端的原始序列x(t)，见下式：

(5)

1.2 单隐层前馈神经网络SLFNs学习算法原理

单隐层前馈神经网络SLFNs学习算法[7]是一种基于构建前馈神经网络的学习机型太的运算，与传统的神经网络模型相比，其有操作简单、参数设置容易以及良好的泛化性能等优点。

对于任意M个不同样本(xi,ti),其中xi=(xi1,…,xin)∈Rm,ti=(ti1,…,tin)∈Rm。若隐含层神经元个数为n,其标准形式如下:

αi=(αi1,…,αin)T

(6)

依据近似原理，对上式的反馈神经网络参数αi,bi,βi进行代迭推算得出：

(7)

式(7)中，Fp(x)为神经元的向量输出值。βi代表其中的“i”层隐藏节点与输出层节点之间的权重向量；G(x)为激励数值；ωi为“i”层隐藏节点与输入层节点之间的权重向量；bi为神经元隐藏层的偏移量数值；因此式(7)还可演化成Hβ=Y。H代表系隐藏层矩阵的输出。通过SLFNs可以定义中阈值与参数权重量，再确定好矩阵H，再来由演化公式β=H+Y进而运算来得到β。其中H+相对的替代了输出的隐藏层矩阵的广义逆理论摩尔-彭罗斯型值。

1.3 耦合PSO与SLFNs量化算法

鸟群觅食算法(PSO)与单隐层前馈神经网络SLFNs学习算法进行耦合作用下，SLFNs学习算法能够发挥较好的结果，然而运算函数中的w阈值与有限权值b、隐藏层节点数对算法的精度影响变化比较大。所以导致算法演算时可能会出现局部的节点失效的现象发生，因此对于SLFNs算法来说需要大量的隐藏层节点，方才达到预设的结果，针对节点数的增加会极大地带来算法的冗余度及运算功率折扣，从而使算法的泛化力滞后。通过耦合鸟类觅食算法PSO能够起到优化单隐层前馈神经网络SLFNs学习算法中的w阈值与有限权值b，从而有效降低模型的复杂度和运算冗余量[7]。鸟群觅食算法(PSO)是1995年被Eberhart和Kennedy发现的一种通过全盘进行优化的运算方式，其原理来源于如果粒子在D维空间内，则可以进行全局优化。

某个种群由n个粒子组成x=(x1,x2,…,xn)，其中第i个粒子表示为一个D维向量xi=(xi1,xi2,…,xiD)T，对于第i个粒子在D维中的位置的暗示，就等同于对于该问题能求得解。并针对该有的目标函数可以求解出粒子的适配值x。式中，第i个粒子的速率值应等于：

Vi=(Vi1,Vi2,…,ViD)T

经过推算该种群的全局极值为:Pg=(Pg1,Pg2,…,PgD)T,粒子通过每作一次叠迭所得到的新的极限值和全局极值的相对(x,y)函数和速率值。若逐步出现饱和状态时，叠迭会出现停止，基体获得新的运算公式(8)、(9)：

(8)

(9)

通过对上述公式进一步的简化流程如下：

1)需要找到定量的输入量值和预期输出向量的引导性迭序样本。

2)依算法PSO与SLFNs学习算法进行耦合要绘制出神经网络拓扑结构。并判断出粒子维度神经输入层与隐藏层和输出层之间是否有选择地进行sigmoid激活函数。

3)种群的产生。该种群由单隐层前馈神经网络SLFNs学习算法加入权限矩阵。和隐藏层的偏置阈值b，通过恢复原始粒子(x,y)函数及速率值，并进行优化范围上值的设置。

4)获取最优参数值。然后依算法PSO与SLFNs学习算法进行耦合程度进行训练其重构后的时序序列，从而能得到最优模型参数，其中最大叠迭值T=500，这个最大迭代次数，种群种数值M=30、学习因子c1=c2=2,r1/r2为两个随机产生的参数，范围为(0,1)，粒子维数D等。

5)确定该种群由单隐层前馈神经网络SLFNs学习算法的方根偏离值作为配合度函数，通过演算出每次粒子的配合度值，进而通过函数解出每个粒子的单一极限值和全盘极限值。

6)确定代迭或极小的错误的最大数字是否被到达，如果那样，中止代迭; 如果不，则进入步骤5)，继续代迭。

2 多维度时变预测EPS模型应用

本文将经验模态分解法、鸟群觅食算法和单隐层前馈神经网络SLFNs学习算法结合在一起，建立多维度时变预测EPS模型对隧道深基坑形变的动态时序序列进行模型分解，其工作流程如图1所示[8]。

图1 隧道深基坑形变多维度时变预测EPS模型流程

若深基坑形变的时间序列为U(t)(t=1,2,…,N), 隧道深基坑形变量预测过程基本如下:

1) 经验模态分解法将监测的基坑形变时序的IMF分量进行分解和本机模式函数(IMF)构件的n个基坑本征时序IMF分量。

Ci(t)(t=1,2,…,N)和一个余rn。

2)将IMF部分和剩余部分分解为两类别，即训练集和测试集，初始化为PSO-SLFNs模型，选择合适的参数。采用假设算法得到函数的项空间重构与冗余的有限权重值，通过PSO-SLFNs预测模型研究训练后的空间重构集，从而获得模型的最佳参数值。利用PSO-SLFNs预测模型学习后的PSO-SLFNs预测模型对各分量测试集进行预测分解[9]。

3)将经过PSO-SLFNs模型预测数据采用权重相加法等叠加法，对基坑形变的一个时序进行预测,从而获得隧道深基坑形变量预测结果。

3 实际工程算例

3.1 工程概况

南宁某商业区市政隧道交通工程改造，见图2中的隧道纵断面图和平面图。根据现场勘察资料得知，地下土层有：不稳定性填土、残积相的黏性土以及古近系泥岩等，其中填土、风化岩及具胀缩性的黏性土、泥岩为特殊性岩土。经勘察该地下孔隙裂隙水主要赋存于古近系粉砂岩孔隙、煤层裂隙中，动态变化主要受季节气候影响，相对稳定。在石园路下穿会展路隧道基坑开挖过程中，石园路南侧高边坡坡体、坡顶发生形变、开裂，坡脚支护桩发生位移，隧道内撑横梁压裂受损，严重威胁周围小区、过往行人、施工人员及来往车辆的安全，因此急需测量其实际形变量以针对性地进行施工作业控制，该基坑的监测点如图3所示。

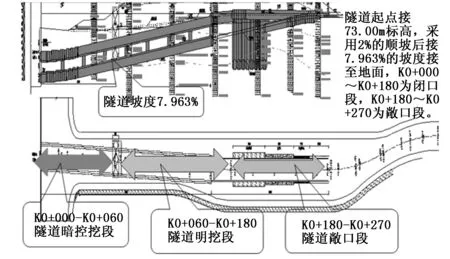
图2 隧道纵断面图和平面图

图3 基坑实验数据的获取及监测平面图

3.2 数据的选取及分析

基于场抓取多处易损点的群集样本，共选取J7监测点K0+000～K0+060; K0+060～K0+1800段的基坑形变原始监测数据进行分析和预测，该隧道深基坑的形变数据如图4所示。

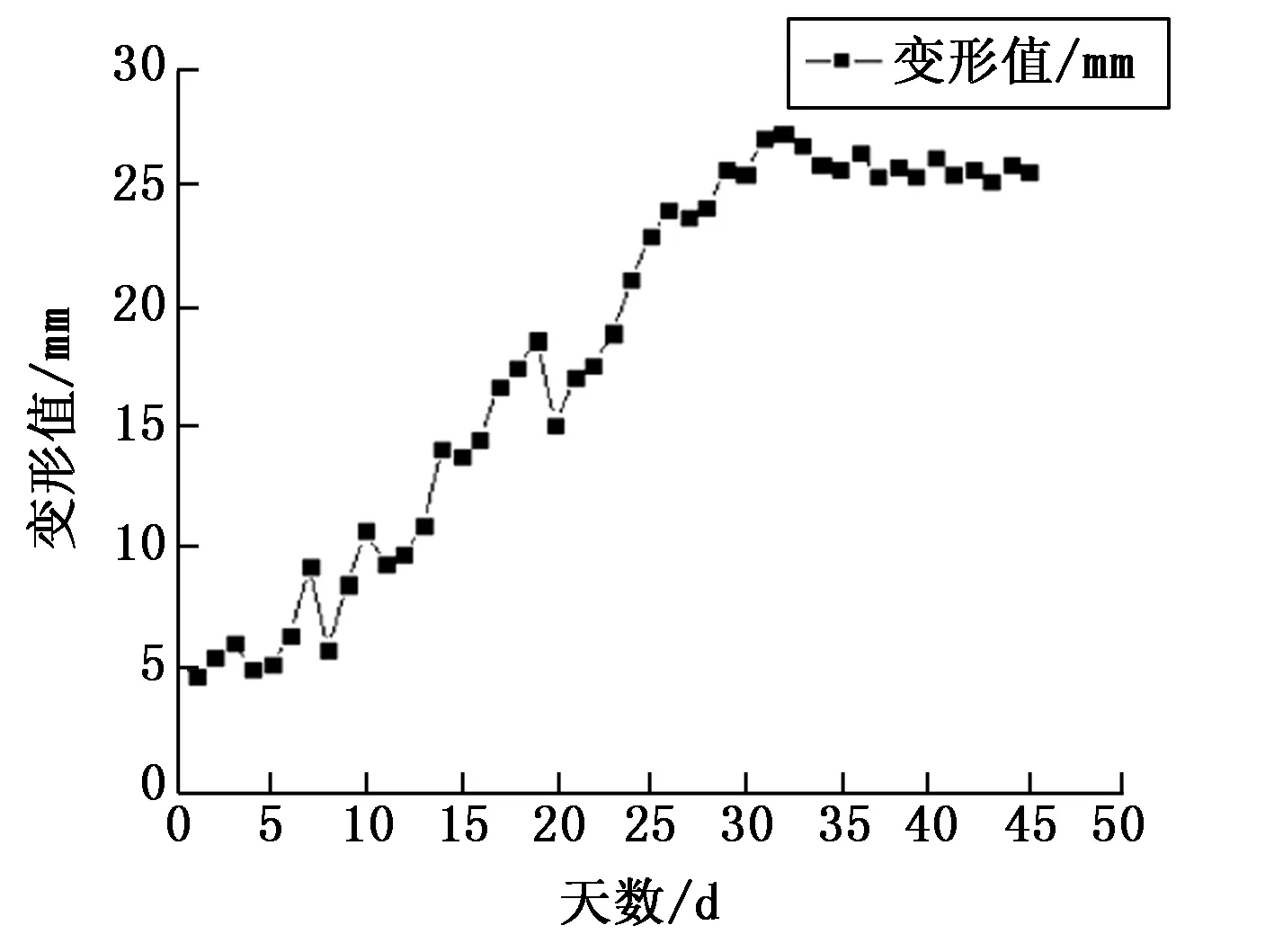
图4 隧道深基坑的形变数据—曲线图

由图4可以看出，在基坑开挖和支护过程出现的形变属于非线性的时序变化，从图中曲线的波动可推断访基坑在施工时形变量也不断地起伏，究其因素有：岩层影响、工艺影响、基坑支护设计影响等等都有可能。首先应用经验模态分解法EMD对形变的情况进行了解，将原来的监测数据进行分解，将原来的高、低频信号源按层次作分拣，从而能高效时剥选出稳定的分量因子，其结果如图5所示。

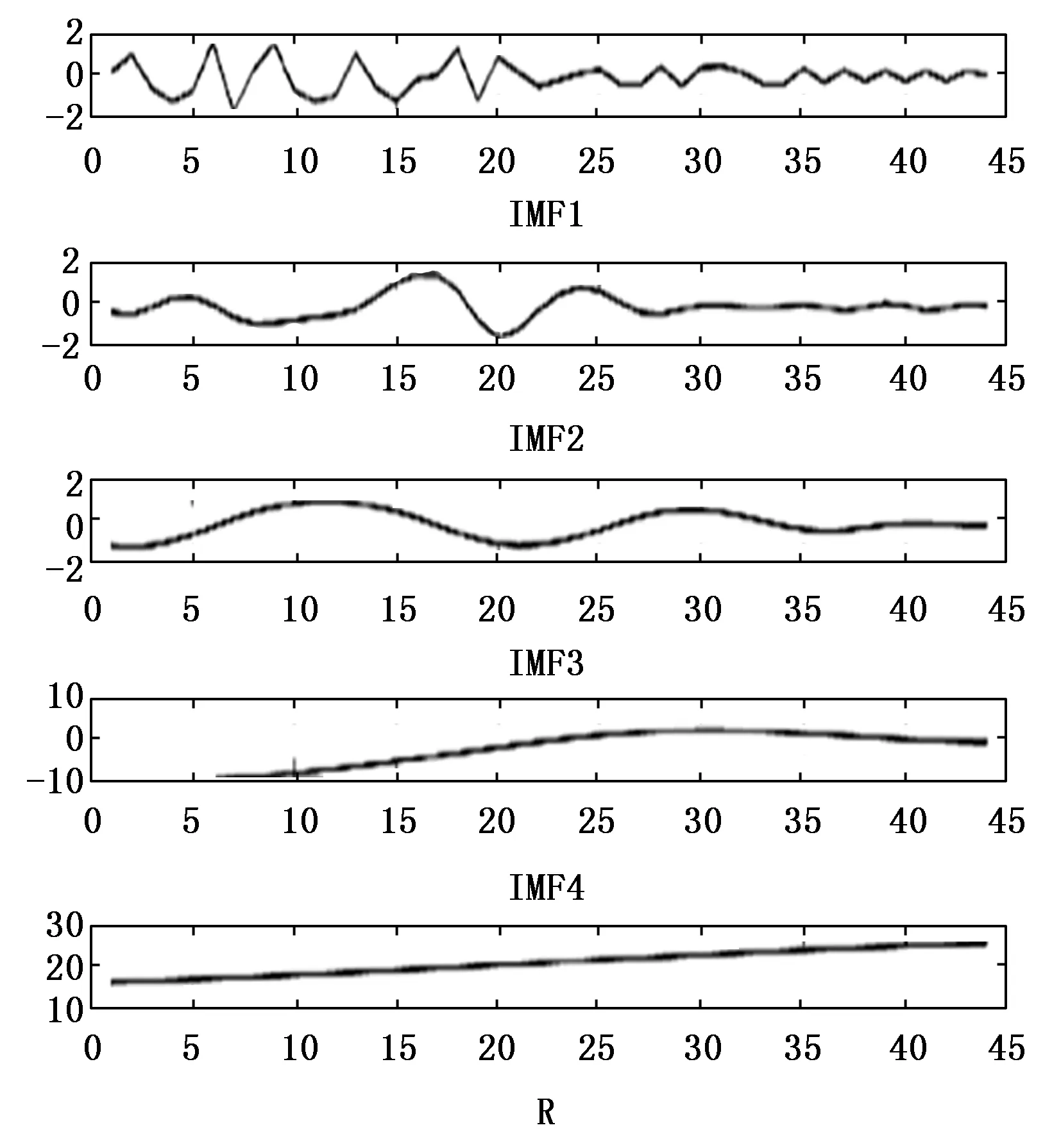
图5 EMD多比例尺分解结果

由图5可以看出，该隧道在基坑开挖和支护过程中基坑的形变所产生的时序序列具有明显的多尺度特征。可见IMF分量由高频到低频的4种比例尺按高频到低频的顺序排列，突出了不同维度受到的波动性。IMF属于高频分量的形变分量。基坑时序噪声的高频分量，这是外部环境、测量仪器等外部环境存在波动的主要原因;IMF2、IMF3属于中度频分量，其波动性大，从而给后续的支护方案控制和整改措施给矛了一定的数据支撑，得知其受时空的变化影响，其中IMF4和R段为低频值量，当中的R段更表现出相对平稳态势，即为残余量值，除基坑形变趋势外，可以基本反映基坑形变的本质特征。通过对基坑监测数据进行经验(EMD)模态分解，可以从多种不同的方面选择基坑时序分解，以及消除原有信号高度频的噪声信息，以获得基坑内的原始信号高频的失真信息，表现出该隧道深基坑形变的实质情况[10]。

对于相位空间重构进行处理，先采取嵌入维度数值在的对应的IMF相位。对各维度的IMF分量和空间量进行分解，重新分解后的嵌入维度如表1所示，并从重构后日测形变量数据，对基坑的形变量进行相应的分析和预测，最后以等权求和算法从而得出最终隧道深基坑形变量预测数据。

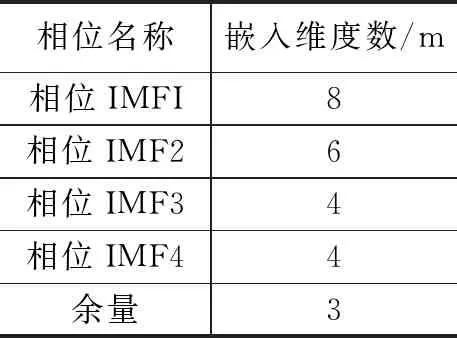
表1 相位空间重构处理数据

3.3 预测结果的论证

针对上述的测量结果现在进行必要的论证，对基坑的形变量求得的数据结果进行相应的分析，以保证该模型的适应性和可行性。分Ⅰ、Ⅱ两组。以Ⅰ组代表记录30 d的序列形变值作为训练集并针对PSO-SLFNs网络模型进行训练，15 d后的重构形变数据采用空间和时间预测模型进行训练并将得到的数据进行相应的形变预测——实测值，然后将Ⅱ组15 d后的监测数据作为EMD-PSO-SLFNs验证值，对验证组和试验组的预测结果进行对比求证，得到曲线图结果如图6所示[11]。

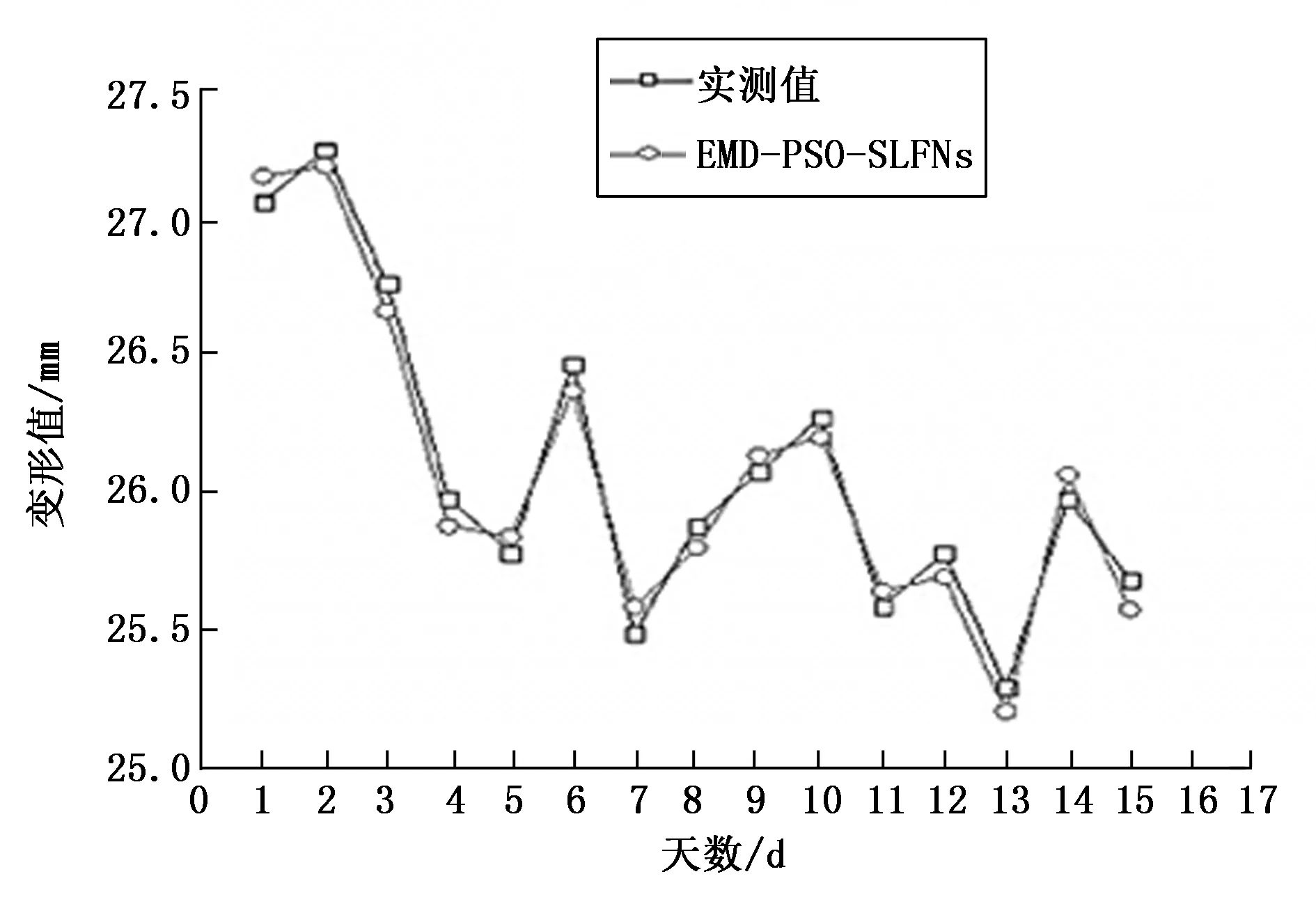
图6 基于EMD-PSO-SLFNs隧道基坑形变曲线图

同时再进一步对隧道基坑EMD-PSO-SLFNs形变预测模型的可靠性进行求证，遂即作EMD算法分解应用于基坑壁的形变产生的非稳定性的时间序列，将上述PSO-SLFNs预测模型预测数据作为验证集。经曲线分解，其结果如图7所示。

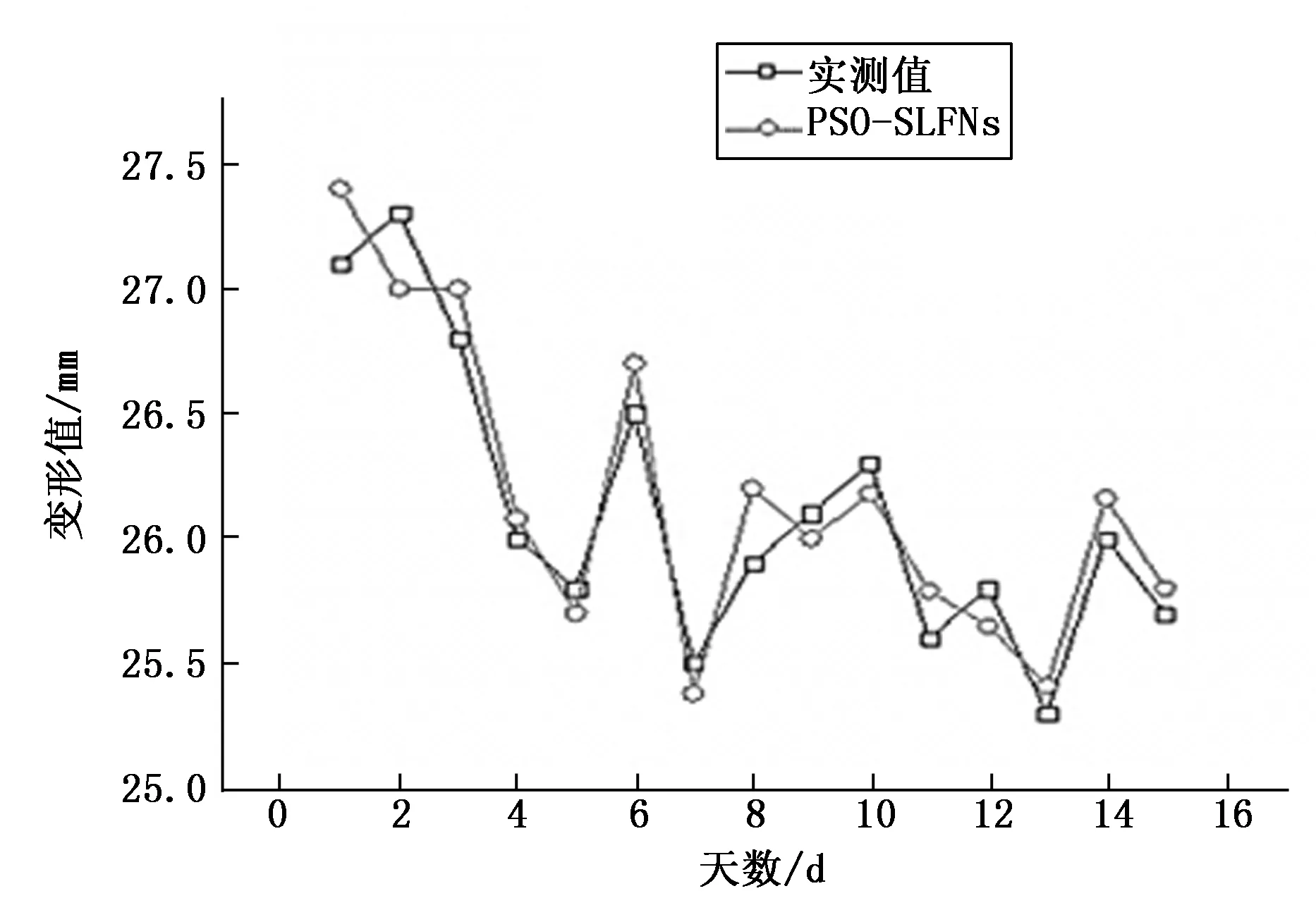
图7 基于PSO-SLFNs的基坑形变曲线图

针对上述两种模型形变量预测曲线图作比较，由图7可知，PSO-SLFNs预测模型在预测隧道地基坑时其是非线性的而且存在着非常大误差因素，而经过EMD算法分解后的PSO-SLFNs预测模型，在非稳态条件下形变量误差很小，近似于现场监测值。所以对EMD-PSO-SLFNs预测模型算法，应用于隧道基坑开挖非线性下的形变量预测具备一定的成效。

该多维时变预测EPS模型的相对误差值作为进一步评价其优越程度指标，得出的结论如表2所示，PSO-SLFNs预测模型相对误差为0.35%～0.78%，平均相对误差为0.68%，其预测精度在现实工程需求下应用仍有不足之处；EMD-PSO-SLFNs预测模型相对误差为0.21%～0.38%，其平均相对误差为0.30%。这样来说，该多维时变预测EPS模型预测的精度更优，能对非稳态变化下的叠迭序列产生更好的适应性[12]。

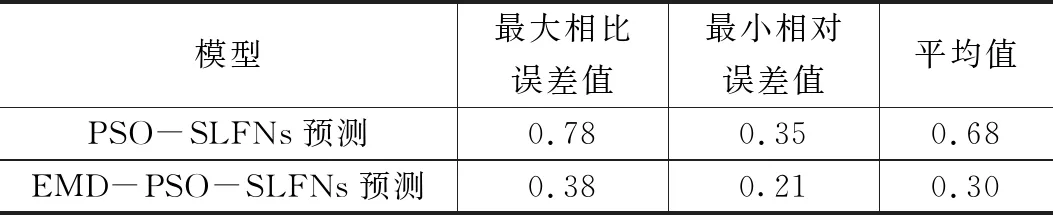
表2 比较两种模态下的测量误差值 %

从该隧道深对基坑形变预测结果进行全局梳理得知，其实测值与监测仪的值相吻合，进而表明该模型能在基坑形变预测中针对出现的非线性形变提供预警参考，从而有效地对基坑周边复杂区域的施工环境起到很好的安全监测作用。

4 结束语

1)很多情况下隧道基坑在施工过程中，由于受到场地条件、地质条件等因素的影响，基坑形变呈现出不稳定的非线性序列而出现形变。运用EMD-PSO-SLFNs组合算法可以利用原有的时间序列对基坑波动和形变的IMF分量进行多维分解表达。从基坑多维形变的角度来分析，可以提升基坑预测模型的准确性。其为同类工程，在非稳定性状态下的测量提供一定的理论依据。

2) 得益于经验模态EMD算法与PSO-SLFNs模型无缝耦合，能抵抗外界如环境影响、时空效应等非静性对隧道基坑形变的种种干扰，而且减少了模型参数选择中人为因素造成的误差。采用经验模态EMD法将基坑形变的原始时空变化序划分4个相对分量区和1个残差分量，通经验模态EMD法将基坑形变的原始时空变化序列分解为4个IMF分量和1个残差分量。再结合PSO-SLFNs模型对基坑形变进行预测，然后用等权重相加法作预测值的交叉筛选，获得终极预测结果。在对模型的相对误差指标进行评价以验证模型的准确性的基础上，证实该多维度时变预测EMD-PSO-SLFNs模型测量结果与现场监测值高度吻合，其平均相对误差精度为0.30%,较用EMD算法有了很大的提升，具有一定实用推广意义。