短丝纤维卷绕牵伸齿轮箱故障信号的图像特征提取方法

(西安工程大学 机关党委，西安 710048)

0 引言

短丝纤维生产线是纺织业中最为重要的步骤之一，棉纤维经除尘干燥、过滤、喷丝、中心环吹、卷绕、牵伸后，最终进入丝桶，形成短丝成品。随着近几年涤纶短丝纤维技术的提高，对短丝生产线也要求越来越高，在短丝生产线中，短丝的卷绕牵伸是成型中最重要的工序，作为传动机构的卷绕牵伸齿轮箱故障会降低短丝纤维的引起牵伸精度，导致短丝纤维产品的质量下降，严重的还会引起设备事故，造成经济损失[1]。卷绕牵伸齿轮箱故障表现为齿轮的断齿、齿面磨损及齿根裂纹等，目前对于齿轮故障诊断的主要方法为在时域[2-3]、频域[4]、时频域[5-6]对指定频带和时段内的振动信号进行分析。P.Hreha等构建了深度学习网络对齿轮箱中传动齿轮的振动特征进行提取，判断齿面磨损状况，对故障进行预测[7]。赵晓清等融合振动多特征信息建立了齿轮箱振动故障诊断模型，并通过模拟分析与实验验证了模型的正确性[8];D. Jena等在小波变换的基础上融合动态变速箱模型来分析齿轮箱振动响应[9];G.Ibrahim等对齿轮箱故障采用Zhao-Atlas-Marks分布与离散小波变换进行综合分析[10]。S.Radhika等在时域中建立齿轮振动信号的AR模型，预测齿轮的状态与故障，通过仿真与实验分析，在轻载荷齿轮的裂纹故障预测中有了较好的效果[11]。近年来，图像识别技术的发展，促进了故障诊断技术与图像识别技术的融合，本文在获取的齿轮振动信号时频特性的基础上，提出了基于双谱图的齿轮故障识别方法，通过分析小波包双谱得到具有明显纹理特征的双谱图，以灰度共生矩阵特征参数为特征向量，对齿轮箱存在的故障状态进行识别。

1 齿轮箱故障机理分析与双谱图的构建

1.1 齿轮箱故障机理分析

作为传动机构的卷绕牵伸齿轮箱是由箱体、主动轮、从动轮等构成的振动系统，主动轮和从动轮的齿面上的摩擦力在润滑情况下可以忽略不计[12]，则齿轮副的振动方程为:

(1)

式中，m1为主动轮的质量，m2为从动轮的质量，X为作用线上齿轮的相对位移，C为齿轮啮合阻尼，k(t) 为啮合刚度，E1为齿轮加载后的弹性变形，E2(t)为故障函数。

式(1)中等式左边的表达式为齿轮传动系统的振动特征，等式右边表达式为激振函数。由于激振函数中的啮合刚度是周期性的变量，由此导致齿轮传动系统在无故障的情况下也会产生啮合振动，该振动信号中还包含啮合频率的谐波分量。激振函数中的k(t)E2(t)项为激励源，将使齿轮产生异常振动。因此卷绕牵伸齿轮箱故障诊断主要为提取激励源所引起的异常振动特征信息。在卷绕牵伸齿轮系统振动信号既有幅值调制又有相位调制，因此其数学模型为：

(2)

式中，rk(t)和φk(t)分别是调幅信号与调相信号，M为齿轮啮合谐波频率的阶数，fm是齿轮的啮合频率，Ak是k阶啮合谐波频率的振幅。

1.2 振动信号双谱图的构建

由式(2)可知，齿轮振动信号由余弦信号叠加而成，谐波处的振幅和啮合频率与齿轮故障的恶化程度成正比。在提取的齿轮故障信号源中，振动信号中存在的齿轮运行状态信息较为全面，但同时也含有一定的高斯噪声和非高斯噪声，将降低故障信号提取的精度。在分析现有齿轮故障信号处理方法的基础上，将小波包分析与双谱分析相结合，采用小波包双谱分析技术对故障信号进行滤波处理。在小波包系数进行阈值处理后，采用小波包变换对振动信号的高频与低频信号进行分解，小波包系数为:

(3)

式中，h为高通滤波器，g为低通小波滤波器，φ(t)是尺度函数，ψ(t)是小波函数。

齿轮箱故障信号一般为振动信号中的低频域[13]，采用小波包变换重构低频带信号Y(t)，其三阶谱定义为:

C3x(τ1,τ2)=E[Y(t)Y(t+τ1)Y(t+τ2)]

(4)

对式(4)进行二维Fourier变换定义为双谱，即:

(5)

由式(5)可知，双谱是复数，其特点是既能反映信号的幅值信息和相位信息又具有较好的纹理特性。

2 基于小波变换的图像融合

由于所获得的齿轮振动信号为多传感器的信号融合，为了全面提取图像纹理特征，本文对小波包双谱分析得到多组双谱图，进行基于小波变换与匹配度的图像融合。将同类或不同类的齿轮故障信号的双谱图进行融合，使得融合后的图像特征更具有典型性[14]。

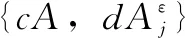
低频子带的融合系数为源图像低频系数加权之和，即:

(6)

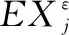
(7)

(8)

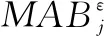
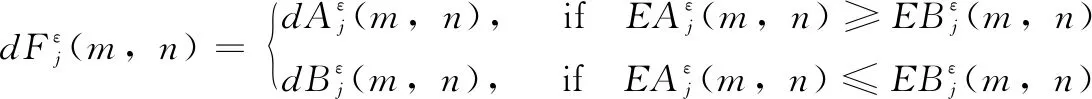
(9)

当图像A和图像B的匹配度较大时，使用显著性度量和匹配度共同决定融合后的小波系数选取，则有：

(10)

小波变换的图像融合的流程如图1所示。

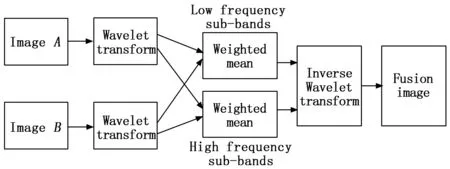
图1 图像融合

由图1可知，在确定源图像A和B的合适小波基的基础上，并对两幅图像进行小波分解，得到低频图像和不同尺度、方向的高频图像，突出高频图像的显著性信息。采用加权法对低频图像进行加权融合；采用匹配法对高频信息进行图像融合。通过融合后的高低频图像信息的小波系数进行小波逆变换，重构融合后的图像。融合后的图像综合了齿轮故障信息。

3 振动信号的特征提取方法

由图1融合后的振动信号图像是灰度变化范围为[0～255]的灰度图，含有丰富的纹理信息，本文通过灰度共生矩阵提取其纹理特征。灰度共生矩阵表示指定方向上一定距离的两个灰度在图像中出现的概率密度[15-16]，图像中两个像素点的位置为(x1,y1)和(x2,y2)，对应的灰度值分别为i和j，在0°、45°、90°和135°的4个方向上，距离为d，获得4个灰度共生矩阵。本文采用角二阶矩、对比度、相关性和熵等4个特征参数进行故障信号的特征提取。

1)角二阶矩W1:

(11)

式中,p为灰度共生矩阵，θ为灰度共生矩阵的生成方向。

角二阶矩又称为能量，是灰度共生矩阵各元素的平方和，表征了图像灰度分布均匀程度和纹理粗细程度，W1越大则纹理粗糙，相反则纹理细致。

2)对比度W2:

(12)

对比度表征图像的清晰程度，图像越清晰，相邻像素对的灰度差别就越大，则W2越大。

3)相关性W3:

(13)

式中,u1、u2为矩阵的均值,σ1、σ2矩阵的方差。

相关性表征图像的纹理方向，如果图像在某方向上纹理较强，则该方向的W3将大于其他方向的值，因此，W3可用来判断纹理方向。

4)熵W4:

(14)

熵表征图像的信息量，图像纹理越多，越复杂，所含有的信息量越大W4值越大。

当距离一定时，通过计算得到的4个方向上的特征参数值受到所选取方向的影响，某个方向的共生矩阵不能完整地描述双谱图的纹理特征，为了完整地描述图像特征，提高故障诊断的精度，对4个方向上的灰度共生矩阵进行加权融合来提取图像纹理特征，则融合灰度共生矩阵为:

S(i,j)=a1p0(i,j)+a2p45°(i,j)+a3p90°(i,j)+a4p135°(i,j)

(15)

式中，S(i,j)为融合灰度共生矩阵，a1、a2、a3、a4为加权系数。

加权系数的数值表征了对应方向上的灰度共生矩阵的显著性，对灰度共生矩阵得到的特征向量作为齿轮故障识别的样本，采用欧式距离作为特征向量分类的可分性判据，其判据值越大则样本空间越容易区分。在小样本统计估计和预测学习中支持向量机(SVM)被认为较最好的理论，本文采用SVM 对齿轮故障双谱图的灰度共生矩阵特征向量样本空间构造出最优超平面，将特征在SVM分类器中使得该超平面与不同类样本集之间的距离最大，从而进行识别分类，达到最大的泛化能力。

4 实验分析

该实验平台为短丝生产线上拉伸牵引的多级定轴减速齿轮箱如图2所示，齿轮箱传动图如图3所示，轴1为动力输入轴，轴2为传动轴，另外系统还包含6个齿轮及一个法兰盘，其中齿轮4、5、6为输出齿轮。短丝生产线工作时，齿轮箱动力源输入动力到轴1，经齿轮1传递到齿轮2，由于齿轮2和齿轮3同轴，因此齿轮2与3的角速度相同，再经齿轮3传递至齿轮4，齿轮4传递至齿轮5，齿轮5传递至齿轮6，齿轮6连接牵引辊，对外部执行机构输出动力。

图2 齿轮箱实验平台

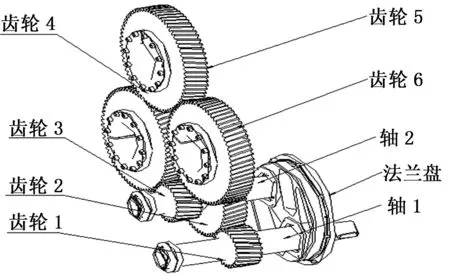
图3 齿轮箱传动图

实验采用输入轴的直齿轮，包括断齿、齿根裂纹2种故障，电机转速为1 600 r/min，在传动轴上布置多个方向的加速度传感器，采样频率为6 840 Hz，采样点数为6 192，每种状态的样本数量为230。

图4描述了被测齿轮在不同故障下的原始振动信号。其对应的双谱图像如图5所示。从图中可以看出，不同工况下变速箱的双谱分布明显不同。图5(a)法向齿轮只在输入轴齿轮啮合频率的前两个谐波(f和2f)处产生能量浓度较高的双谱。图5(b)断齿双谱分布在3f附近具有明显的脉冲分量。在图5(c)中，除了输入轴齿轮啮合频率f和2f处的能量峰值外，双谱图像中还存在大量背景噪声。在图5(d)中，观察到在主能量f和2f附近有清晰的边带能量峰值。虽然在不同条件下齿轮振动信号的双谱图像中发现了一些差异，但从图5中很难直接区分每个齿轮故障。

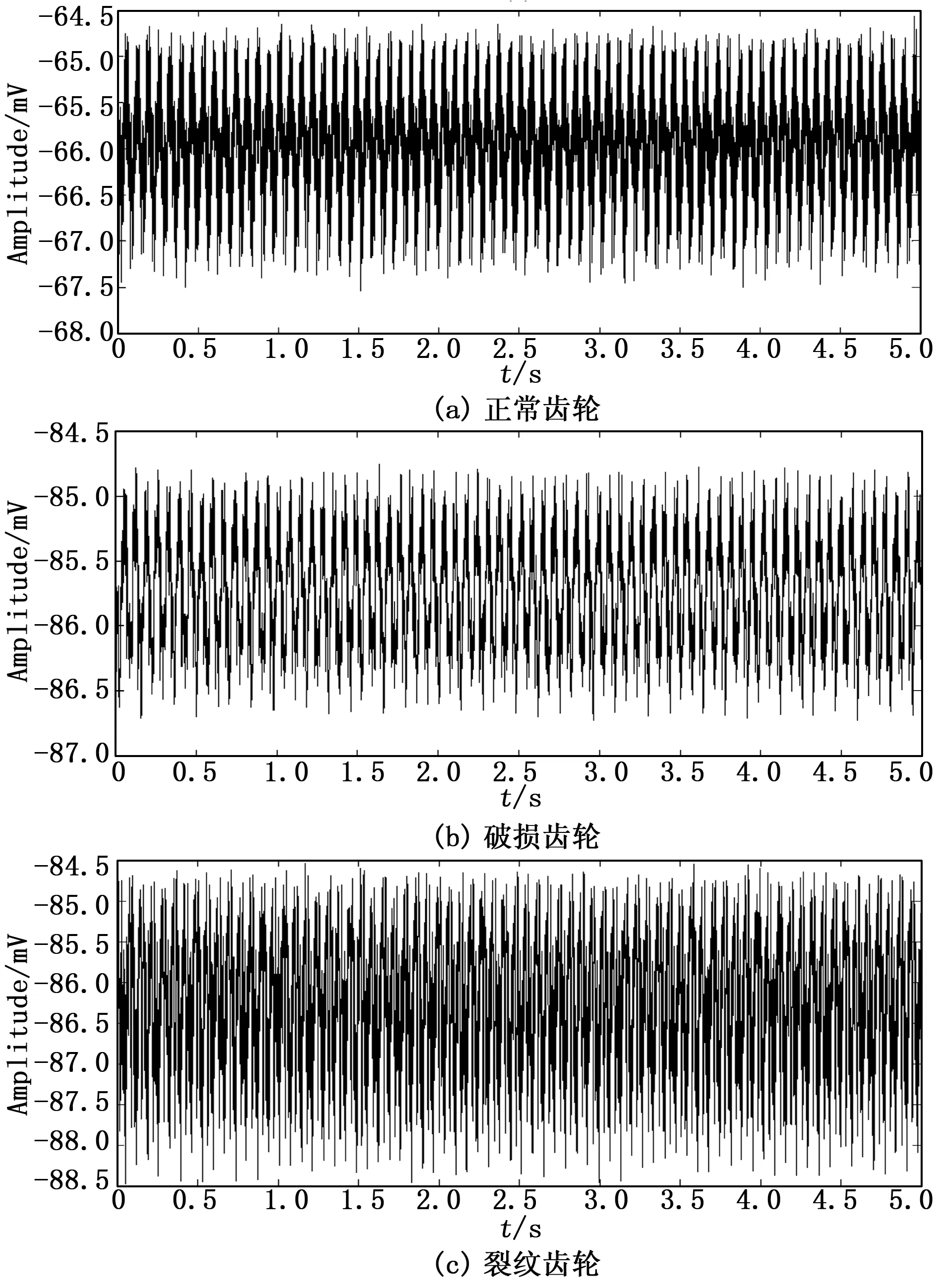
图4 齿轮的原始振动信号

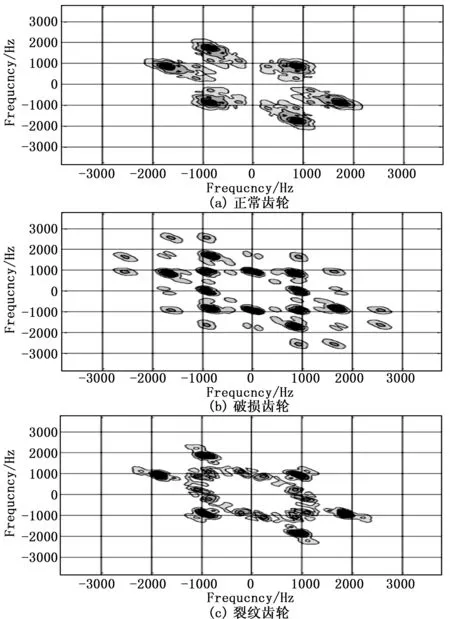
图5 齿轮振动信号的原始双谱纹理图

对原始图像进行小波包双谱处理，基于小波包双谱处理的图像如图6所示。可以看出,相比之下，图5和图6中的噪声干扰在小波包双谱处理后明显减少，图像的纹理更加清晰，和4个齿轮操作条件的主要能量峰值集中在f和2f相脱节的齿轮啮合频率输入轴。由于高阶谱的对称性，4种工况下双谱分布呈中心对称。这些观测结果对于采用图像处理技术进行齿轮故障检测具有重要意义，因为齿轮具有中心对称双谱分布。

由图6可知，融合后的双谱图的纹理特征比图5所示的单方向双谱图更加丰富，具有两个方向上综合的纹理特征。

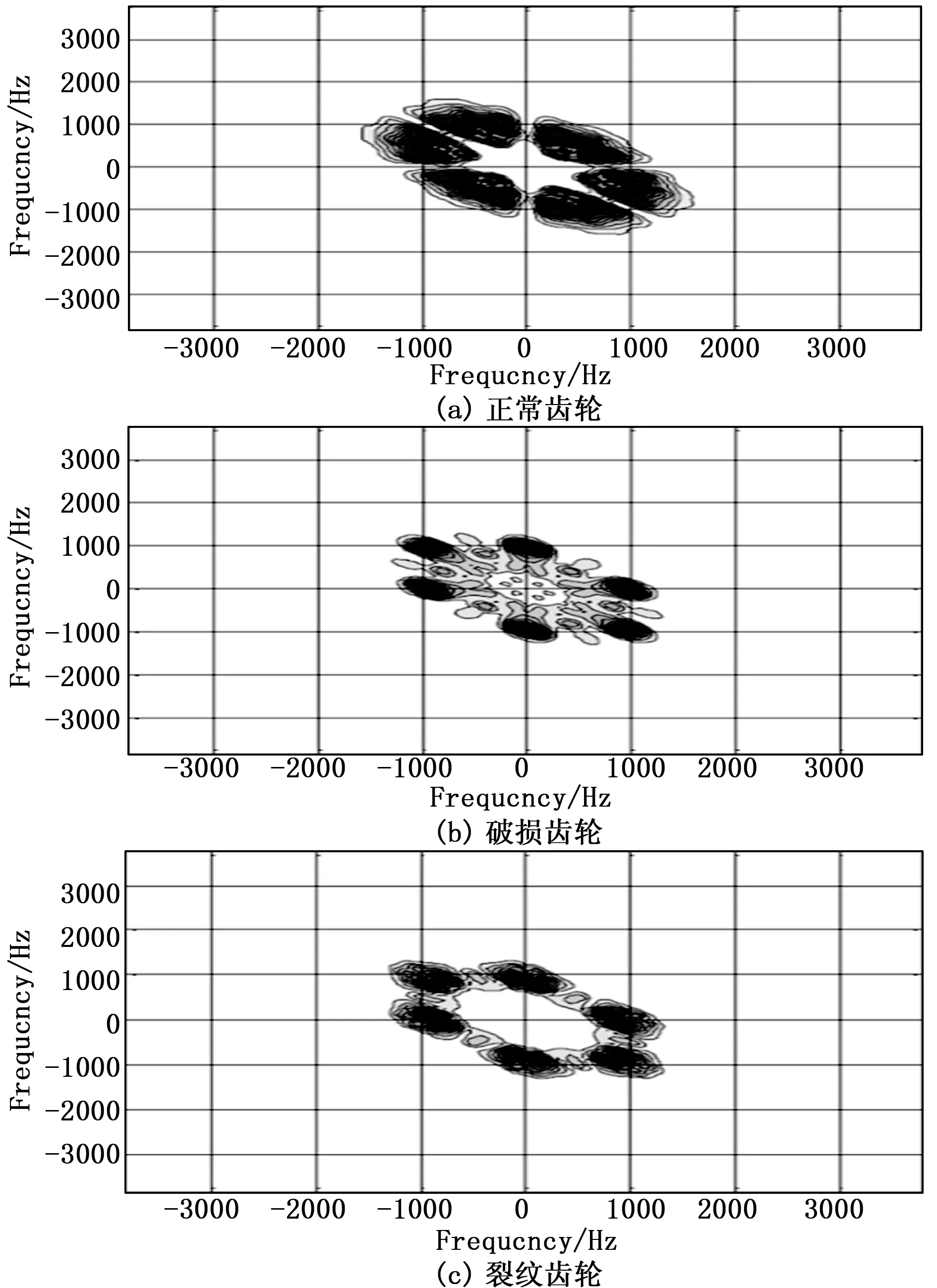
图6 小波包双谱分析后的振动信号图像

融合图像2.4部分列出的4个特征(W1～W4)由GLCM提取，然后将GLCM特征输入SVM分类器进行故障识别。在SVM模型的训练过程中，以变速箱各工况的130个样本作为训练数据集，以各工况的另外100个样本作为测试数据集。表1列出了使用不同结构参数的支持向量机进行故障检测的结果，表1给出了各齿轮工况下的故障检测结果。

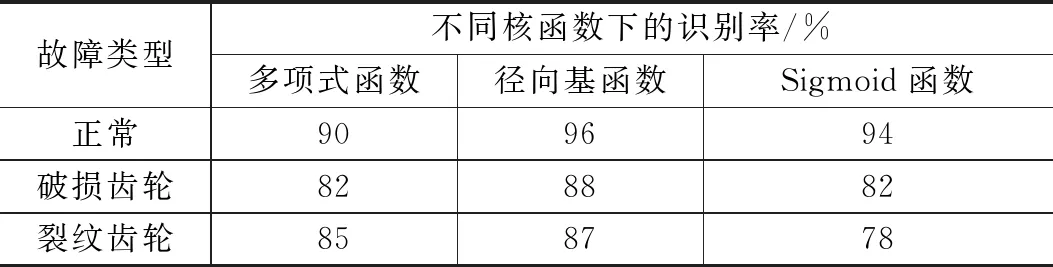
表1 不同核函数下的分类识别率

由表1可知，在不同故障类型的信号中，由于正常齿轮啮合的振动信号边频少，双谱的纹理特征清晰，故正常类别的识别率较高，齿根裂纹与断齿的双谱纹理相对模糊，故识别率较低。通过对比可以看出，径向基核函数的综合识别效果优于其他两类核函数。

5 结束语

1)本文将图像识别技术应用到纺织设备的齿轮故障诊断识别中，通过获取振动信号的高阶谱信息，提取故障特征，采用SVM 对齿轮故障特征进行分类识别，达到了稳定的识别效果，为齿轮箱故障诊断提供了新方法。

2)采用小波包双谱分析齿轮振动信号，有效消除振动信号中的高斯噪声和非高斯噪声，获得具有稳定纹理的双谱图。通过基于小波变换与匹配度的图像融合算法，将两个方向的振动信号的双谱图进行融合，其具有了两个方向的综合特征。

3)通过灰度共生矩阵的图像纹理特征，提出了基于加权平均的灰度共生矩阵融合方法，以灰度共生矩阵的4个特征参数作为特征向量，以支持向量机(SVM)的图像分类识别算法，实现了对齿轮的断齿、齿根裂纹等故障的识别，识别率均在85%以上。