基于MedDRA系统的药物安全性多重比较贝叶斯层次模型构建及应用*
东南大学公共卫生学院流行病与卫生统计学系(210009) 陈振明 李太顺 杨嘉莹 王诗远 刘 沛
【提 要】 目的 在处理药物不良事件的安全性分析时会面临多重性问题,基于不良事件类型间的相似性,应用贝叶斯层次模型进行多重比较。方法 利用MedDRA词典的层次结构构建贝叶斯层次模型,比较不同层次结构对模型的影响及其收缩作用。分析超过数概率进行统计推断的优势,以便标记出潜在的不良事件信号。结果 贝叶斯层次模型使得不良事件间的数据可以借用同一层次内的信息,达到收缩数据的作用,收缩的程度与层次结构有关。使用后验超过数概率进行分析使得结果更具临床意义。结论 本研究将贝叶斯层次模型引入不良事件的安全性分析中,并以实例说明其统计特性,为解决多重性问题提供了新思路。
药物安全性数据的多重比较无论是对频率统计还是贝叶斯统计都是较为棘手的问题之一[1]。药物安全性数据常常包括众多不良事件(adverse events,AEs),而这些不良事件又因为分属于特定器官和系统而存在着相关性,即需要在不满足一般统计方法独立性假定的条件下进行不良事件的多重比较。贝叶斯统计通过建立层次模型可有效处理这类复杂结构数据[2]。国外学者对此进行了深入研究,并取得了良好效果[3-4]。国内目前尚未见到这一方面的报道。究其原因,笔者认为可能与目前国内许多临床试验安全性数据结构不满足构建贝叶斯层次模型的条件有关。随着国家对临床试验数据标准化和电子化要求的提高,由人用药物注册技术要求国际协调会(international council for harmonization,ICH)开发的国际医学标准术语—MedDRA引入了我国。MedDRA的标准化编码和按临床意义划分的五级层次结构,为应用贝叶斯层次模型提供了条件。在此情况下,探讨药物安全性数据多重比较的贝叶斯层次模型构建具有现实意义。
原理与方法
1.MedDRA及层次结构
MedDRA是在医药事务管理活动中使用的一套医学标准术语[5],其编码为五级层次结构,从低到高依次为低位语(lowest level term,LLT)、首位语(preferred term,PT)、高位语(high level term,HLT)、高位组语(high level group term,HLGT)、器官系统分类(system organ class,SOC),它允许研究者从各种角度对数据进行检索与归类。以“流鼻涕”为例,对应的LLT编码为“流鼻涕”,PT为“鼻漏”,HLT为“上呼吸道症状和体征”,HLGT为“呼吸道症状和体征”,SOC为“呼吸系统、胸及纵隔疾病”。由于SOC和HLGT主要按解剖学,生理学和病因学分类,所以在同一SOC或HLGT类别下的PT具有更高的相似性,这为构建贝叶斯层次模型提供了条件。
2.贝叶斯层次模型构建
令AEbj为第b个SOC类型下第j个PT发生的AEs,其中b=1,2,3…,b,j=1,2,3…,k;令Nt、Nc分别为Abj中试验组(t)和对照组(c)的样本含量,Ybj、Xbj为试验组和对照组的AEs发生人数,相应的AEs发生率分别为tbj和cbj。按照Berry等[3]建议的方法构建三层次贝叶斯模型。
首先对Ybj,Xbj构建二项分布似然函数,即Ybj~Binom(Nt,tbj),Xbj~Binom(Nc,cbj)。然后采用OR值作为比较指标,构建如下logistic回归模型:
其中γbj是对照组的AEs发生率中率比的logit变换值,θbj为试验组与对照组的logit差值增量,即log(OR)。显然,θbj=0表示在不良事件类型AEbj中,试验组与对照组的发生率无差别,即cbj=tbj。
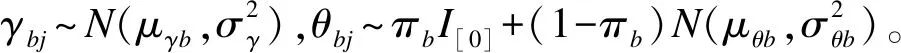
采用贝叶斯方法建立无效假设H0为OR=1,备择假设H1为OR>1。如果OR>1的后验概率大于0.5[7],即H1成立的可能性大于H0,则接受H1,认为两组间存在差异,试验组AEs的发生风险高于对照组。反之若OR=1的后验概率大于0.5,则接受H0。
3.超过数概率
本研究构建的层次模型不仅可以计算OR>1的后验概率,也可以获得其他感兴趣参数的后验概率,如OR>2。尽管OR>1表示试验组的风险高于对照组,但不一定具有临床意义。因此可以使用后验超过数概率(exceedance probability)来标记不良事件信号,即P(ORbj>d*|data)>p[6]。d*和p的取值可以根据实际临床意义进行界定,如d=1.5或2,p=0.5或0.8。p的取值越大,则需要的证据强度越大。
4.软件实现及编程关键语句
根据上述原理,本文采用OpenBUGS、R软件编写计算程序。为构建贝叶斯层次模型,首先利用OpenBUGS语句:X[i]~ dbin(c[b[i],j[i]],Nc),Y[i]~ dbin(t[b[i],j[i]],Nt)构建Ybj,Xbj的似然函数。每一个SOC层中的πb采用pi[k]~ dbeta(alpha.pi,beta.pi)构建,混合先验部分先定义p0[i]~dbern(pi[b[i]]),然后根据示性函数选择对应的概率分布,即theta1[b[i],j[i]]~ dnorm(mu.theta[b[i]],tau.theta[b[i]]),theta[b[i],j[i]]<-(1-p0[i])*theta1[b[i],j[i]]。若读者需要完整程序,可直接联系作者索取。
结 果
1.MedDRA分类及频率统计分析结果
数据来源于笔者参与的b型流感嗜血杆菌(Haemophilus influenzae type b,HIB)疫苗III期临床试验,评价疫苗应用于2月龄至5周岁儿童的安全性和免疫原性。该试验为非劣效的随机对照试验,分为2~5月龄、6~11月龄、1~5岁3个年龄亚组,选择6~11月龄为分析对象,该组中试验组、对照组人数各为250人。不良事件类型分布于代谢及营养类疾病,感染及侵染类疾病,呼吸系统、胸及纵隔疾病,皮肤及皮下组织类疾病,全身性疾病及给药部位各种反应,胃肠系统疾病共6个系统。
对AEs的发生情况分别按照SOC/PT,HLGT/PT的层次结构进行编码分类,试验组和对照组的不良事件采用频率统计的Fisher精确概率法进行假设检验,结果如表1所示。
由表1可知该研究共有6个SOC,14个HLGT,24个PT,最后一列给出了利用频率统计的Fisher精确概率法得到的P值。其中两组间差异存在统计学意义(P≤0.05)的AEs类型为上“呼吸道病毒感染”(P=0.042)和“呕吐”(P=0.011)。若采用Bonferroni法对P值进行校正,P≤0.005,则所有的AEs都没有统计学差异。

表1 HIB疫苗III期临床试验基于MedDRA分类的不良事件发生情况
*表示P≤0.05,有统计学差异。
2.贝叶斯层次模型分析
(1)后验概率
按照SOC/PT、HLGT/PT间的层次结构得到各个AEs中OR=1和OR>1的后验概率,如表2、表3所示。除了“呕吐”,SOC/PT层次结构中其余AEs的P(OR=1|data)均大于0.5,即倾向于认为试验组的不良事件发生率与对照组没有差异。其中“呕吐”的P值最小(0.004),得到OR>1的后验概率大于0.5(0.718),即频率统计和贝叶斯统计都认为组间存在差异。但不良事件“上呼吸道病毒感染”的P值小于0.05,得到OR>1的后验概率却小于0.5(0.231),此时贝叶斯模型相比于Fisher精确概率法更倾向于认为“上呼吸道病毒感染”在两组间没有差异。
HLGT/PT得到的结果如表3所示,与SOC/PT得到的结论相似。相比于SOC,HLGT的层次划分更为细致,它的层次结构更符合临床概念,为此也更加合理。但由于层次更细会使得每一个HLGT下的PT数量减少,使得大部分HLGT下只有1个或2个PT,模型所带来的收缩效果也会减小。
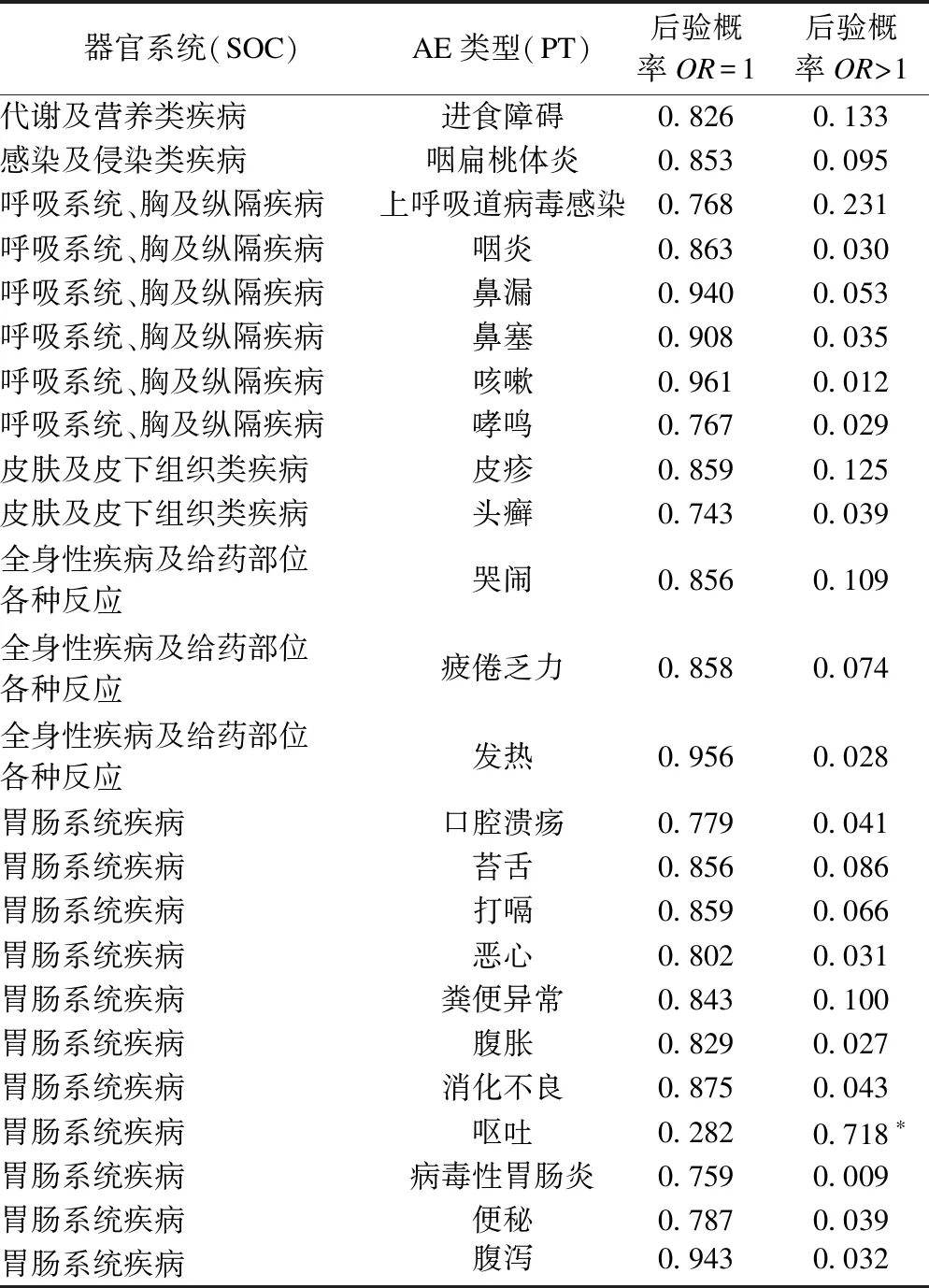
表2 HIB疫苗III期临床试验以SOC/PT为层次结构的贝叶斯后验概率
*P(OR>1|data)>0.5,组间存在差异。

表3 HIB疫苗III期临床试验以HLGT/PT为层次结构的贝叶斯后验概率
*P(OR>1|data)>0.5,组间存在差异。
(2)超过数概率
以该研究为例,在后验超过数概率中分别取d*=1.5,d*=2,d**=0.02,d**=0.05,p=0.5比较SOC/PT、HLGT/PT中不良事件“上呼吸道病毒感染”、“呕吐”的后验超过数概率,如表4所示。随着d*的增加,后验概率逐渐下降,但下降的程度依据模型的层次结构而有所不同。如“呕吐”,在SOC中P(ORbj>2|data)=0.676,而在HLGT中则为0.767。
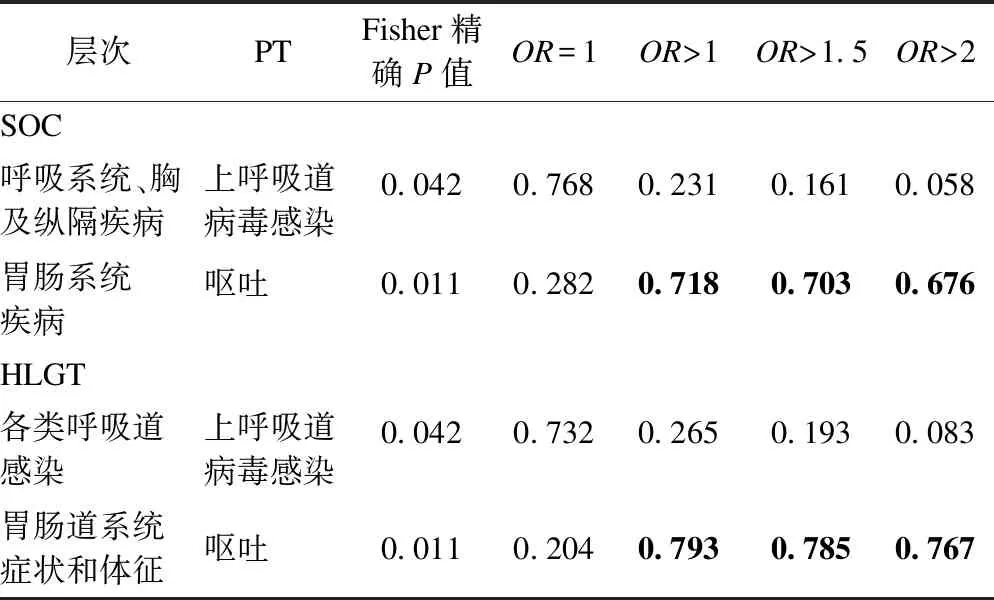
表4 不同层次结构的超过数概率
3.贝叶斯层次模型和频率统计比较
无论是对频率统计还是对贝叶斯统计,OR值及相应的可信区间都是进行安全性评价的重要统计推断指标,图1展示了用频率统计与贝叶斯方法得到的SOC/PT、HLGT/PT中“上呼吸道病毒感染”与“呕吐”的OR值结果。相对于频率统计,贝叶斯统计得到的OR值更小,置信区间范围也更窄。这一方面说明贝叶斯层次模型在安全性评价中的点估计结果没有频率统计那样“激进”;另一方面说明贝叶斯层次模型在安全性评价中的区间估计结果比频率统计更为精确。

图1 贝叶斯层次模型与频率统计的OR值及其95%可信区间
讨 论
在临床试验的安全性分析中,多重比较问题不可避免。在经典统计中,直接采用Fisher精确概率法进行假设检验容易导致假阳性。因此在处理这类问题时通常是采用Bonferroni法对P值进行校正,但当比较的类型增多时,过低的P值又会导致假阴性的增加。这样的调整在样本量较大的时候往往是比较保守的[8],只有在极端情况下才能得到具有统计显著性的结论。另一种方法是采用假发现率(false discovery rate,FDR),将假/真阳性比例控制在一定范围内以达到二者的平衡[9]。Mehrotra等人[10]基于这种方法,将不良事件按身体器官划分,结合调整后的P值减少了多重性的影响。采用贝叶斯方法则可充分利用数据的层次结构信息,通过在相同层次内借用信息,进而提高统计推断的效率。除了贝叶斯层次模型外,有研究者也提出了蒙特卡罗方法[11]与贝叶斯筛选方法[12]解决多重性问题。
本研究提示,对同一个不良事件采用贝叶斯层次模型和经典统计可能会得到不同的结果,如SOC/PT结构中的“呕吐”。这是由于经典统计在计算P值的时候假定不同PT间AEs的发生是独立的,而贝叶斯层次模型则认为“呕吐”这一不良反应在其所属的SOC/PT结构中并不独立,通过引入与其它AEs的相关性使结果更符合临床实际。本研究显示,模型的层次结构不同,同一AE的后验概率也有所不同。如“呕吐”在SOC中的超过数概率低于HLGT,这说明模型层次可影响贝叶斯后验概率,这一结果与Xia等人[6]的研究相同。
本研究另一值得关注的结果是,相对于频率统计,贝叶斯统计得到的OR置信区间范围更窄。这是因为贝叶斯层次模型将不同AE类型间的生物学联系考虑在内,通过层次模型向平均水平的收缩提高了OR估计的精度[13]。这在某些亚组样本含量较小或出现极端数据(0%或100%)时,其优势更为明显[14]。
相比于传统方法仅检验OR是否等于1,本研究采用OR大于1的超过数概率作为安全性评价指标,有其独到的优势。显然前者只能做出是否有风险的定性判断,而后者则为研究者根据临床实际同时进行定性和定量判断提供了灵活的方法。如若某一不良反应危害较大(如出现血液系统损害),则应给予较小的d*值以减少漏判,而对于危害较轻的不良反应则可给于较大的d*值。若对统计推断的可靠性要求较高,则可以提高p的界值。研究者可以从临床意义(d的大小)和统计推断的可靠性(p的取值)两个方面做出临床决策。使用贝叶斯层次模型分析药物安全性时,需注意其应用条件。模型要求随机变量满足可交换性,组内和组间的收缩基于数据服从独立同分布假定,因此需要结合实际判断数据是否满足前提假设。

