基于边界面的多隔舱筒形基础动力分析

吴诗阳，曹永勇

(1. 中冶华天工程技术有限公司，江苏 南京 210019；2. 南京水利科学研究院，江苏 南京 210029)

风能作为可再生能源和清洁能源的代表被越来越多的国家关注。我国离岸50 km范围内可开发风能资源为7.58亿kW，是陆上实际可开发风能资源储量的3倍。随着海上风电的大力发展，对风电基础的要求越来越高，目前常用基础形式有重力式、单桩、多桩、三脚架、导管架群桩、浮式基础和负压筒形基础。其中负压筒形基础由于施工工艺简单、成本低、一体化施工、二次使用等优点，在最近几年得到大力发展。Liu等[1-4]研究了筒形基础在不同荷载组合下的极限承载力，给出了基础破坏时的空间屈服包络面。Amin等[5-6]基于摩尔-库伦弹塑性模型，分析筒径、贯入比对筒体极限承载力的影响。Zhang等[7]通过离心模型试验研究指出，筒形基础在长期荷载作用下会发生较大的沉降和侧向位移。Bagheri等[8]研究了循环荷载和单调荷载作用下筒形基础的变形行为，指出在筒盖附近会发生较大的水平位移。国内学者的研究主要集中在栾茂田和练继建团队，取得了很多学术成果。范庆来等[9-11]采用位移控制法和Swipe试验加载方法，获取了V-T,HM,H-V-M,V-H-T等不同荷载组合下的破坏包络面，并推导了地基承载包络线的表达式，为国内筒形基础的极限设计提供参考依据，加快了筒形基础的发展。刘莹等[12-14]基于动力三轴试验，考虑软土弱化效应，将弱化后的土体强度代入到计算中，从而考虑循环荷载作用下筒形基础的承载力。戚蓝等[15]基于等效线性模型研究了近海风电筒形基础风机解耦的地震响应特性。于通顺等[16]基于摩尔库伦弹塑性本构模型，研究了风、波浪、海流荷载共同作用下筒形基础的响应规律和基础周围孔隙水压力的变化情况。

以上学者都是基于拟静力法研究筒形基础的承载力和变形，鲜有关于筒形基础在动荷载作用下的响应研究。仅有的动力研究也是采用等效线性模型，或摩尔库伦理想弹塑性模型，并不能很好地反映动荷载下土体的应力应变关系。本文基于边界面弹塑性动力本构模型，采用自回归线性滤波法模拟脉动风速谱，研究风荷载作用下多隔舱筒形基础的动力响应和土体孔隙水压力变化情况。

1 基础结构模型

筒形基础主要由筒体、盖板和过渡段组成。其中筒体直径为30.0 m，高12.0 m，筒壁厚25.0 mm，筒内共有7个隔舱，12块分舱板，每个分舱板长7.5 m，筒体和分舱板材料均为钢材。盖板高1.2 m，梁形结构，材料为钢筋混凝土，过渡段呈圆锥体结构，高18.8 m，材料为钢筋混凝土，筒形基础整体结构见图1。钢和钢筋混凝土的弹性模量分别为206和36 GPa，密度分别为7.85和2.45 g/cm3，泊松比分别为0.28和0.19。

图 1 筒形基础结构（单位：m）Fig. 1 Structure of bucket foundation （unit: m）

2 主要荷载分析

2.1 风荷载模拟

风荷载也称风的动压力，是空气流动对工程结构所产生的压力，大小与风速的平方成正比。作用于结构上任意一点的风速可表示为平均风速和脉动风速之和。平均风速可用Davenport提出的指数模型[17]进行模拟：

脉动风是时间t的随机过程，可看成具有零均值的平稳高斯随机过程。本文采用自回归线性滤波法进行脉动风速的时程模拟。空间相关的M个点顺风向脉动风速时程随机列向量的AR模型可表示为：

式中： X =[x1,···,xM]T， Y =[y1,···,yM]T， Z =[z1,···,zM]T， ( xi,yi,zi)为空间第i点坐标，i= 1,2,···,M；为AR模型阶数，这里取4是模拟风速时程的时间步长；为AR模型自回归系数矩阵，为阶方阵；为独立的随机过程向量，可由下式表示：

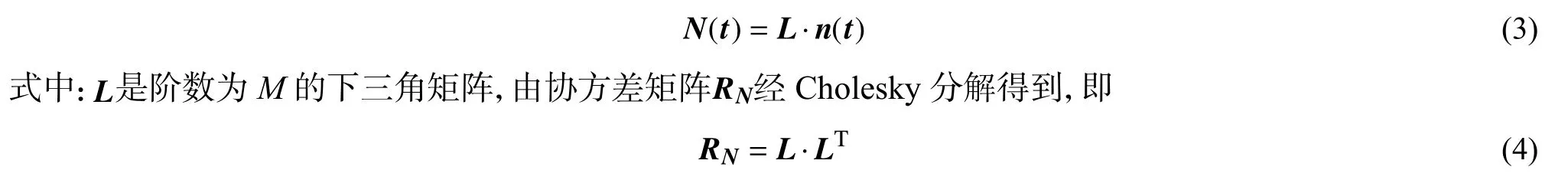
式中： H =[I,H1,···,HP]T，为 (P +1)M×M 阶矩阵，是阶单位阵；为 P M×M 阶矩阵，其元素全部为0，为(P+1)M×(P+1)M阶自相关Toeplitz矩阵，写成分块矩阵的形式为：

根据描述的AR模型即可求得脉动风速的时程曲线，为了便于计算，运用MATLAB软件编写计算程序，其计算参数为：10 m处风速33.0 m/s，截止频率12 Hz，地面粗糙度系数取0.005，采样间距0.125 s，总模拟时间300 s。采用双对数坐标，给出了塔筒中点脉动风速功率谱密度与目标谱的对比曲线，如图2所示。

图 2 模拟脉动风速功率谱分析Fig. 2 Spectrum analysis of turbulent wind simulation

从图2可以看出，塔筒中点脉动风速在零值上下波动，符合平稳随机过程的特性，并且模拟的风速谱与目标谱吻合较好，尤其在高频部分，因此该方法可模拟脉动风速，能反映脉动风速时程曲线自相关随机特性。

得到脉动风速时程曲线后，将各计算点的平均风速和脉动风速叠加，即可得到该点的瞬时风速，然后通过下式计算作用在结构上的风荷载：

风机是高耸结构，风速具有空间相关性，不同位置风速不同，本文采用文献[16]建议的方法将风机离散化，等效成20个点，塔架8个点，叶片12个点。这20个点作为风荷载施加点承受风压，整个风机结构受到的风荷载为这20个点承受风压的总和，图3即为这20个点风荷载的总和。

图 3 风荷载的时程曲线Fig. 3 Time history curve of wind load

3 动力响应分析模型

筒形基础采用线弹性本构模型，其中筒体采用壳体单元模拟，盖板和过渡段都采用实体单元模拟。筒形基础周围的土体采用零弹性区单椭圆边界面模型，可以很好地反映土体循环动力特性。土体为粉土，边界面模型参数取值如下：临界状态线CSL在p-q应力空间的斜率=1.13，临界状态线CSL在e-lnp空间中的斜率=0.09，回弹指数=0.018，泊松比=0.3，模型常数=20，初始孔隙比=1.14。为了考虑土体孔压变化对基础稳定性的影响，采用三维8节点位移-孔压耦合单元。借助商业软件ABAQUS进行有限元数值分析，为了有效消除边界效应的影响，整个模型的尺寸，取径长为5倍筒径，深度为3倍筒高，如图4所示。

图 4 有限元计算模型Fig. 4 Numerical model of finite element

4 计算结果分析

4.1 筒体位移变化

筒体中心点水平位移和转角的时程曲线见图5。从图5可以看出，水平位移和转角均随着时间的增加而产生波动现象，这与荷载的时程曲线分布类似。随着时间的持续，水平位移和转角逐渐增大，在11级暴风的工况下，筒形基础水平增幅约为1 cm，符合变形要求。但若在长期风荷载作用下，筒形基础的水平位移和转角可能会呈上升趋势，因此需要对基础进行长期监测。

图6是筒体右侧点的竖向位移时程曲线。从图6可见，竖向位移并没有像水平位移和转角那样出现较大的波动，随着加载的持续，呈斜向上发展趋势，没有减弱的迹象，这是因为筒体发生倾斜时，较大的筒体自重会进一步导致筒体发生沉降，形成一个“勺形”的沉降区。

图 5 筒体中心点水平位移和转角的时程曲线Fig. 5 Time history curve of horizontal displacement and corner of the bucket center

取1，10，100和300 s作为研究的时间节点，不同深度筒壁对应的水平位移如图7所示。从图7可以看出，不同时间节点的筒体水平位移变化规律相似，沿着筒壁深度，筒体的水平位移不断减小，顶部位移远远大于端部位移，可知筒体已发生转动。同时随着时间的持续，筒体的整体位移不断增加，这与上述结果一致。

图 6 筒体右侧点竖向位移的时程曲线Fig. 6 Time history curve of right point about bucket foundation

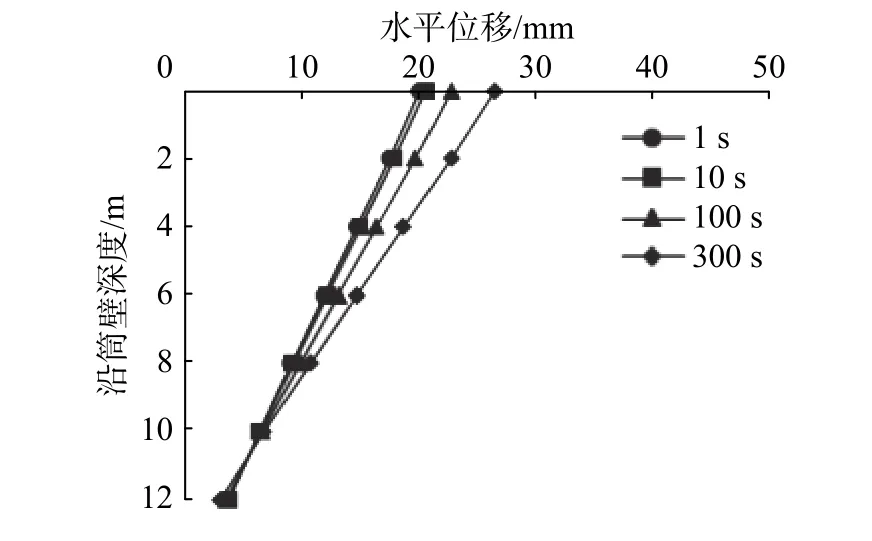
图 7 不同时间节点的筒体水平位移Fig. 7 Horizontal displacement of different time nodes

4.2 土体孔压变化

脉动风荷载在短暂的作用过程中，土体来不及排水，容易积累孔隙水压力，因此土体孔压的变化势必会影响土体的强度，从而影响筒形基础的整体稳定性。取埋深10 m处4点，分别距中心轴4，11，18和30 m，其孔压的分布如图8和9所示。

图 8 筒内部两点孔隙水压力时程曲线Fig. 8 Time history curve of pore pressure about two points in a cylinder

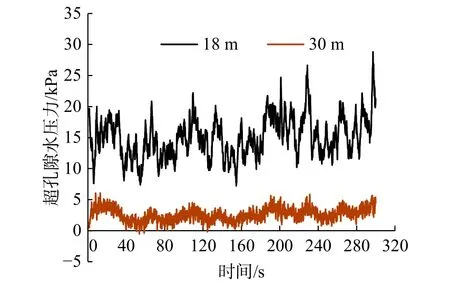
图 9 筒外部两点孔隙水压力时程曲线Fig. 9 Time history curve of pore pressure about two points outside a cylinder

从图8和9可以看出，在风荷载的作用下，超静孔隙水压力（下文简称超孔压）随着时间的持续缓慢增长。基础内部土体，越靠近中心轴，超孔压波动和累积越小，这是因为筒体内部有较多隔舱，舱内土体基本被分舱板约束住，使土体和分舱板具有良好的协调变形能力，整体刚度偏高，从而导致筒体内部土体超孔压波动较小。反观筒体外侧土体，越靠近筒壁，土体的超孔压值越大，波动也越强烈，这是因为筒形基础在风荷载作用下，筒壁处与土相互作用最为强烈，土体易受动荷载的作用发生破坏，此时土体的超孔压变化频繁。逐渐远离筒壁与土的相互作用区时，超孔压变化较小，并趋于稳定。从图8和9还可以看出，筒内部的超孔压要小于筒壁附近处的超孔压，这也体现出在基础内部设置分舱板的优势。

图10为超孔压沿不同路径的变化，其中路径1是筒内深度2 m处沿半径方向变化，路径2是筒内深度10 m处沿半径方向变化，路径3是筒外半径18 m处沿埋深方向变化。

从图10可以看出，不同深度处超孔压沿径向变化的规律相似，越靠近筒壁处超孔压值越大，即在筒壁附近超孔压波动较为强烈，土体更易发生破坏，同样在静力极限分析中，筒壁处土体容易出现变形过大而发生破坏。从图10还可以看出，筒外侧土体的超孔压随着深度增加逐渐减小，这是因为筒外侧土体没有分舱板的约束，在泥面处，筒体与土体相互作用强烈，土体的超孔压迅速累积，随着深度增加，围压不断增大，相互作用相继减弱，则土体不易积累孔压，因此会出现超孔压随深度的增加逐渐减小的现象。

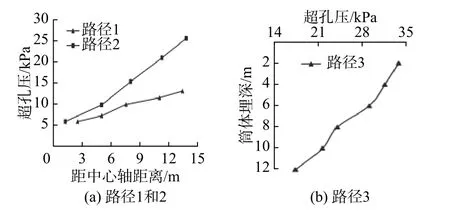
图 10 超孔压沿不同路径方向变化值Fig. 10 The excess pore pressure changes in the direction of the path

4.3 p′-q空间的应力路径

筒壁与筒外侧土体相互作用较为强烈，取筒壁外侧土体分析该土体应力路径发生的变化，如图11所示。从图11可以看出土体有效平均正应力随着加载的持续逐渐减小，并逐渐向临界状态线靠近，但并未达到破坏的标准，由此可以判断土体在极限荷载作用下并没有发生破坏。由于荷载的随机性，应力路径的变化同样表现出不规则性，这和在循环荷载作用下有很大区别。同时，不同深度处的土体，其应力路径有些许差别，在3 m深度处偏应力随着加载的持续逐渐增加，应力路径左斜向上发展；7 m处这种趋势逐渐减弱，偏应力保持整体稳定；而在11 m处有很大区别，偏应力随着荷载时间缓慢减小，应力路径呈左斜向下发展，土体达到破坏阶段所需时间无限延长。可出看出，3 m处土体比11 m处土体更早达到破坏状态，这与孔压产生较大波动有关。

图 11 应力路径变化Fig. 11 Stress path change

4.4 基础的弹塑性应变分析

筒壁处土体容易受到荷载作用发生破坏，并导致筒体失稳，在筒体做摇摆运动时，筒壁处与土相互作用也最为强烈。取筒壁处对应深度1，5，9和11 m的点，分析该点土体的弹塑性应变，各点的应变分量时程曲线比较如图12所示。其中选取水平应变、垂直应变和剪应变作为主要的研究对象。规定应变压为正、拉为负，从图12可知，在荷载作用过程中，水平应变和垂直应变都是增长的，且在量级，其中表面处的水平应变发展速率大于其他各点，且沿着深度方向逐渐减小并产生负值，若取绝对值比较，深度9 m处的应变最小。从静力极限分析中得知，在筒体转动中心附近处几乎没有水平位移产生，因此土体很难受到挤压而产生塑性应变。通过应变由正转负的过程，可以看出筒体在动荷载作用下发生转动。而从图12（b）中垂直应变值可以看出，表层土体会因筒体挤压发生隆起，而筒底附近的土体会因为筒体下沉处于向下受拉的趋势。从图12（c）中可知，不同深度的剪应变增长规律是相似的，但表面处的剪应变大于其他点位，这与水平应变类似。通常土体发生破坏的应变量级需要达到，不同深度处土体的应变都未达到破坏的量级，但随着时间推移，表层土有可能会最先达到破坏量级。

图 12 弹塑性应变时程曲线Fig. 12 Time history of elastic-plastic strain

5 结 语

（1）采用AR自回归线性滤波法可以很好地模拟脉动风速的随机性，且与目标谱吻合较好。

（2）随着加载的持续，复合筒形基础的水平位移、转角和竖向位移会不断增加，同时基础外侧土体的变形也会随之增长，浅层土体会比深层土体更早达到破坏状态。

（3）由于分舱板的影响，基础内部土体孔压发展缓慢且小于外侧土体孔压，沿筒径方向，越靠近筒壁孔压越大；筒外侧土体，沿深度方向，埋深越大，越不容易积累孔压。

（4）在50年一遇的极限风荷载作用下，筒形基础周围土体并未发生破坏，随着加载的持续，土体的应力路径逐渐向临界状态线靠近。