改进加权质心算法用于煤矿井下人员精准定位

周孟然，黄曼曼，闫鹏程，胡 锋，卞 凯

(1.安徽理工大学电气与信息工程学院，安徽 淮南 232001；2.安徽理工大学计算机科学与工程学院，安徽 淮南 232001)

煤矿井下环境复杂，当发生井下事故时，会造成通讯不畅，信息阻断等问题。因此，在第一时间获取井下人员定的信息尤为重要[1]。

目前大多数井下人员定位采用的是无线传感网络技术[2]。无线传感网络节点定位分为测距和无需测距两大类，基于RSSI接收信号强度的测距方法对硬件要求低，定位精度高，与质心算法相结合，可以准确的计算出未知节点坐标[3]。但RSSI信号在传输过程中易受环境的影响，定位误差大，精度不高[4]。为了提高定位精准，一般可以从两方面着手。

一方面，是对RSSI进行信号优化处理，减小信号误差。文献[5]提出基于聚类算法分析的高斯混合滤波，有效提高测距精度。文献[6]采用粒子滤波对RSSI值进行优化预处理，降低了定位误差。这些滤波算法对RSSI信号值进行优化，最终得到平滑稳定的RSSI值。

另外一方面就是对质心算法的改进，文献[7]提出了一种基于动态权重指数的四点定位算法，提高了定位精度，但动态权重因子因环境的不同而不同，难以广泛的应用；文献[8]提出一种利用信号强度的比值作为加权因子的加权质心定位算法，该算法的精准度提高了很多。文献[9]提出以RSSI值解算距离倒数和作为质心算法的权重，以及加入修正系数，使整体定位误差减小了。

上述文献中虽然提高了井下人员定位精度，但煤矿井下易受多径衰减、电磁噪声等因素的影响，仍不能满足井下人员的精确定位。因此本文提出了改进的加权质心算法，该算法在传统质心算法的基础上，增加另外两个信标节点，以其中两个最近的信标节点作为基准，对所求出的坐标点进行2次质心算法，同时变更各个坐标的权重值。实验结果表明，该算法有效的降低了测量误差，提高了定位精度,满足于煤矿井下人员定位。

1 井下人员定位系统与传输模型

1.1 井下人员定位系统架构

煤矿井下环境复杂，辐射源及设备繁多，使得煤矿井下人员定位难度系数增大。根据煤矿井下环境的特点，构建不同的网络模式，以满足人员的精确定位。

井下人员定位系统构架包括：地面监控中心、定位服务器、数据交换机、多组AP设备和人员标签等。地面监控中心实时监控井下状况，出现问题及时解决；数据交换机实现数据的传输和交换；多组AP设备依据煤矿井下巷道路径呈网格状排列，具有静态的IP,对携带人员标签的人员进行读取信息及定位；人员标签与AP进行无线通信，获取位置信息，计算出自身位置，其系统框架如图1所示。

1.2 无线信号传输路径模型

RSSI测距是根据接收端接收的信号强度，结合无线信号传播模型，把测量的信号值转化为距离值。因此，不同的环境，选择不同的无线信号路径损耗模型。目前，井下人员定位使用最广泛的是对数正态分布分布模型，且综合性强，故本文选择对数正态分布模型，其模型公式如式(1)所示

(1)

式(1)中:F(s)是距离接收端s处的路径损耗；F(s0)是距离接收端s0处的路径损耗；λ是路径损耗指数；ω是高斯随机变量。

1.3 卡尔曼滤波

由于煤矿井下环境复杂，RSSI信号易受煤矿井下环境的影响，因此，需对RSSI信号进行滤波，减少环境带来的干扰。本文选用卡尔曼滤波算法，对RSSI信号值进行预先处理，得到平滑稳定的信号后，再带入公式(1)计算信标节点到未知节点的距离。

卡尔曼滤波算法整体过程：

1)预测阶段：用k-1时刻的最优估计预测k时刻的状态变量

(2)

(3)

2)更新阶段：利用现在时刻的测量值来更正预测阶段估计值

(4)

(5)

(6)

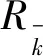
卡尔曼滤波是一个不断地剔除不满足条件的噪声的递归过程。最终得到平滑稳定的RSSI信号值，从而提高了井下人员定位的精度。

2 质心算法

质心定位算法是非测距算法，扩展性高，使用广泛。它以未知节点为中心，接收信标节点发送的信号，通过路径衰减模型计算信标节点到未知节点的距离。

2.1 传统质心算法

传统质心算法以未知节点为中心，各个有效信标节点围成一个区域，求其信标节点的平均值，即为未知节点的坐标。

2.2 一般加权质心算法

传统的质心算法方法容易，计算简单，但误差较大，对于煤矿井下人员定位精度不高，而且每个信标节点到达未知节点的距离不一样，则对未知节点的影响就不一样，即分配的权重不一样。传统的质心算法不能满足于煤矿井下人员的精确定位，故引进加权质心算法。

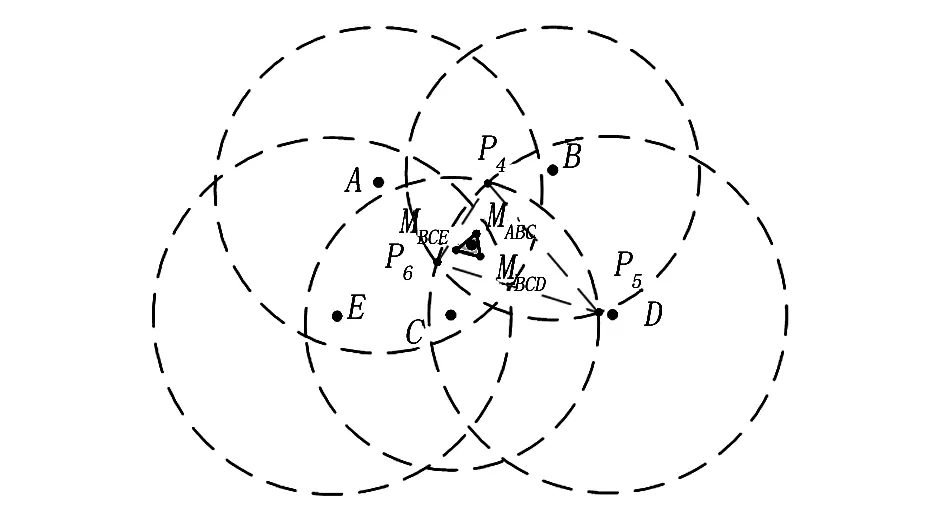
加权质心算法以距离未知节点最近的三个信标节点A、B、C为圆心画圆，三圆相交于一个区域，交点为P1(x1,y1)、P2(x2,y2)、P3(x3,y3)，且对应的半径分别为sA、sB、sC，设未知节点为MABC(XABC,YABC)。所建模型如图2所示， 其中，D、E为第四个和第五个距离未知节点最近的两个信标节点。

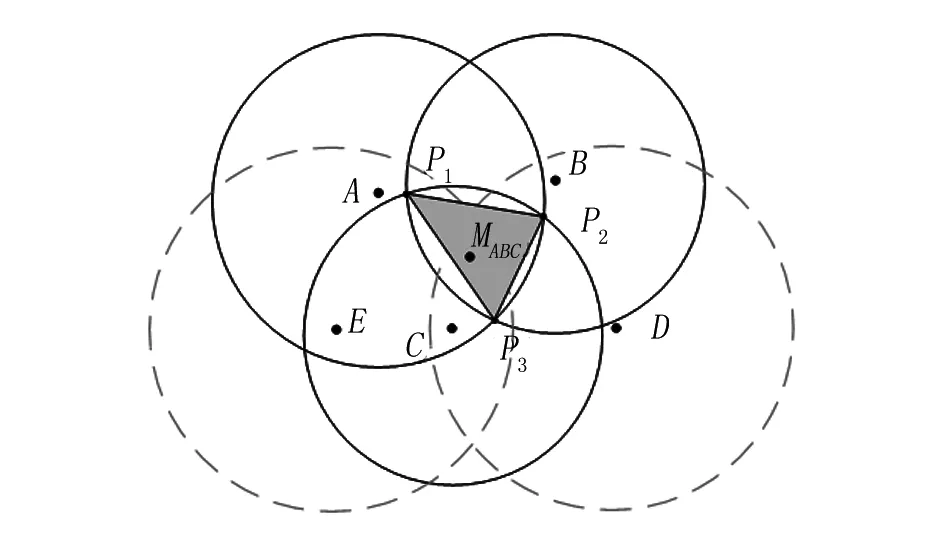
图2 A、B、C三圆相交图

由三圆相交求解出交点P1(x1,y1)的坐标，同理,可求解出P2(x2,y2)、P3(x3,y3)的坐标。三个交点到未知节点MABC(XABC,YABC)距离不同，故对未知节点的影响就不同，分配的权值也就不一样。由于交点P1、P2、P3分别是由两个圆相交而成，故交点P1点受B、C两点的影响，权值分配为1/(sB+sC)，同理可得，P2的权值分配为1/(sA+sC)，P3的权值分配为1/(sA+sB)，因此，未知节点的权值分配表达式为

(7)

2.3 修正加权质心算法

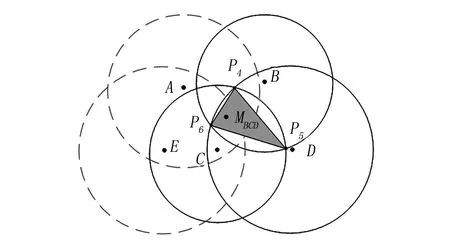
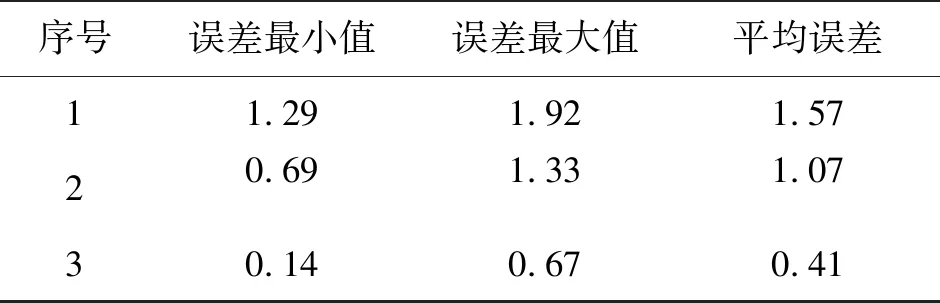
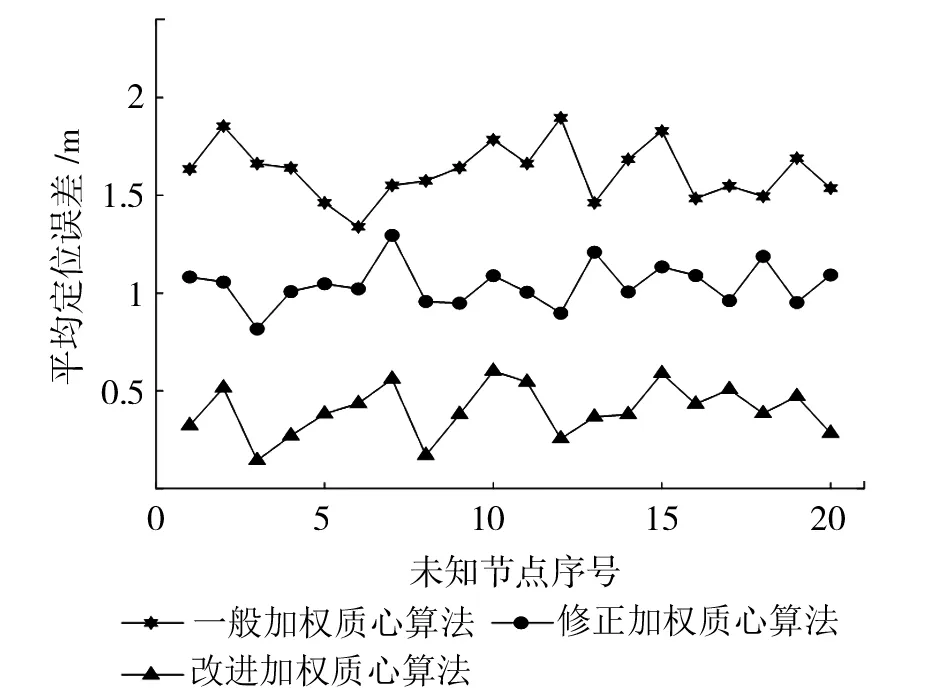
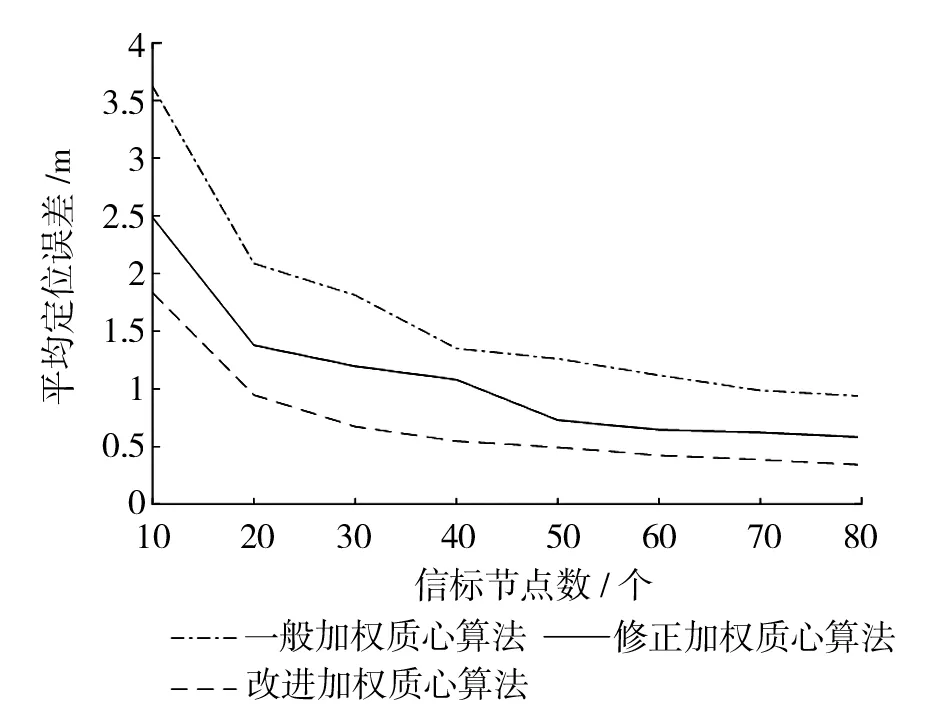
虽然加权质心算法提高了定位精度，但仍然存在不足，比如，两个信标节点A、B到未知节点的距离分别为st、sr,且st

最终改进后的加权质心算法公式为

(8)

式中：β为修正指数。

2.4 改进加权质心算法

修正的加权质心定位算法仍然存在着误差，因此，本文提出利用距离未知节点除A、B、C外最近的信标节点D、E，以五个信标节点中最近的两个信标节点B、C为基准，分别于其余三个信标节点组成三圆相交状态，其建立的数学模型如图3、图4所示，B、C、D和B、C、E三圆分别相交,相交的点为P4、P5、P6和P7、P8、P9,且圆D的半径sD,圆E的半径为sE。最后通过三次修正的加权质心算法求解出另外两个标量MBCD(XBCD,YBCD)，MBCE(XBCE,YBCE)，如图5所示。

图3 B、C、D三圆相交图

图4 B、C、E三圆相交图

图5 最终未知节点估计图

把这三个坐标量同时再带入加权质心算法公式中，且带入的加权质心算法的各个分配的权值不同，由于求解出的点MABC(XABC,YABC)、MBCD(XBCD,YBCD)、MBCE(XBCE,YBCE)是分别由ABC、BCD、BCE三圆分别相交而求得，且求解出的坐标点无法发射信号，未知节点无法由信号强度计算出未知节点的到MABC、MBCD、MBCE距离半径。因此，无法使用改进后的质心算法的权值分配，但又由于点MABC、MBCD、MBCE是由圆ABC、BCD、BCE相交求解出来的坐标，故他们的权值可由三圆的半径倒数之和构成，即坐标MABC(XABC,YABC)所分配的权值为1/sA+1/sB+1/sC，其加入修正指数为(1/sA+1/sB+1/sC)β；同理可得，坐标MBCD(XBCD,YBCD)最终所分配的权值为(1/sB+1/sC+1/sD)β；坐标MBCE(XBCE,YBCE) 最终所分配的权值为(1/sB+1/sC+1/sE)β，未知节点M(X,Y)最终表达式为

(9)

式中：G1=(1/sA+1/sB+1/sC)β，

G2=(1/sB+1/sC+1/sD)β，

G3=(1/sB+1/sC+1/sE)β。

3 仿真实验结果

为验证本文改进算法的有效性和准确性，利用Matlab 2017b进行实验仿真，测试一般加权质心算法、修正加权质心算法和改进加权质心算法，然后进行对比分析。首先，模拟建立一个100m×100m二维正方形区域，信标节点和未知节点都由随机函数生成，随机分布在正方形区域，通信半径为30m。

通过实验仿真模拟，对每种算法测量300组，求出其平均误差、最大误差和最小误差。由表1中可看出三种算法的平均误差值，序号1表示一般加权质心算法，平均误差最大；序号2表示修正加权质心算法，平均误差1.07m；序号3表示改进加权质心算法，平均误差最小，定位精度最高。

表1 误差分析 m

图6是实验中取固定的20个未知节点，分别带入三种算法，求其平均误差。实验结果表明：改进加权质心算法的误差值最小，定位精度明显高于一般加权质心算法和修正加权质心算法。

图6 三种算法平均误差

由图7可知，改进算法的平均误差，随着信标节点数不断增加，逐渐趋于稳定，且平均误差值明显低于一般质心算法和修正加权质心算法。

图7 信标节点数量对平均误差的影响

4 结论

本文对于提出的改进加权质心算法，以模拟仿真实验验证了改进算法的稳定性和准确性。首先，通过卡尔曼滤波对信号值进行滤波优化，得到光滑稳定的RSSI值，然后结合路径衰减公式，把信号值转化为距离值。最后，利用改进的加权质心算法计算出未知节点的坐标。由实验结果可以看出：(1)改进加权质心算法的平均误差为0.41m ，理论上已经满足煤矿井下人员精准定位；(2)改进加权质心算法比一般加权质心算法、修正加权质心算法定位效果更好，求解出的坐标更接近未知节点真实坐标。改进加权质心算法定位精确，稳定性强，有效的降低了定位误差，能更好的应用于煤矿井下人员定位。