两关节压电机械臂刚柔耦合振动特性分析
马天兵,陈 凯, 刘 健, 杜 菲
(1.安徽理工大学机械工程学院,安徽 淮南 232001; 2.安徽理工大学矿山智能装备与技术安徽省重点实验室,安徽 淮南 232001)
目前,机械臂在工业、航空以及医疗等领域应用广泛,但机械臂运动时会产生一定的振动,影响其定位精度,为减少机械臂振动,需要首先了解振动产生的原因和机理,并对机械臂的振动特性进行分析[1-2]。国内外一些学者从动力学模型入手,对机械臂振动特性进行研究,文献[3]考虑关节柔性建立了双连杆机械臂模型,并对其进行了振动控制,具有重要的工程价值;文献[4]以绝对节点坐标法对柔性梁结构进行了建模,探究了刚性、柔性坐标共享的可能性;文献[5]利用假设模态法和汉密尔顿原理建立了机械臂柔性部分动力学模型,获得了末端负载的残余振动,为主动残余振动控制提供了参考。这些研究提出了多种可靠的建模方法,但是,仅对一定条件下的振动特性进行了分析,并没有考虑不同因素对其振动的影响关系,分析不够全面。除上述研究之外,文献[6]采用传递矩阵与机械导纳建立了柔性机械臂的动力学模型,研究了复杂柔性机械臂空间多维振动特性;文献[7]提出了一种基于变形旋量理论的动力学建模方法,探究了机械臂空间变形耦合和扭转变形对振动特性的影响;上述研究虽然考虑了不同属性因素对机械臂振动特性的影响情况,但研究大多侧重仿真,缺少实验的验证与对照,并且对实测信号的振动特性分析不够具体。
针对上述问题,本文选取刚柔机械臂作为研究对象,利用拉格朗日方程以及假定模态法对其进行动力学建模,并考虑关节柔性对模型进行优化,仿真分析两种模型的振动情况;搭建压电两关节机械臂实验平台,选取转速、电机配置等因素设计正交试验进行振动测量,并利用信号处理方式,分析振动信号,探究不同因素对机械臂振动特性的影响。
1 考虑关节柔性的建模及仿真
1.1 动力学模型的建立
为提高模型精确度,减少运算复杂度,在保证建模准确性的前提下,作出如下假设[5]:
1)只考虑柔性机械臂的横向振动,忽略其轴向变形和剪切变形;
2)假定横向变形为小变形;
3)机械臂的长度远大于其截面面积;
4)忽略重力、阻力等因素对系统的影响。
刚柔两关节机械臂的简化模型如图1所示,XOY为惯性坐标系,X1OY1、X2O2Y2分别为固连于杆1和杆2上的动坐标系,杆1是长度为l1的刚性臂杆,杆2是长度为l2的柔性臂杆;在O处设置驱动电机1,在其带动下,杆1绕着O点旋转,其转动惯量为J1,加载力矩为τ1,转动角度为θ1,在杆1另一端设置驱动电机2作为关节,并连接杆2以O2点为原点作旋转运动,转动惯量为J2,加载力矩为τ2,转动角度为θ2,关节处质量为md。同样的,P点在X2O2Y2坐标系中的存在变形,假设挠度形变量为y,则P点变形前位置为(l2,0),变形后为(l2,y)。
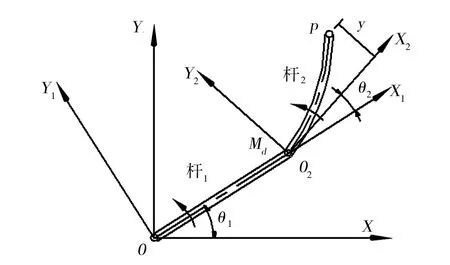
图1 刚柔两关节机械臂的物理结构模型
则P点在X1OY1中的位置为(l1+cosθ2l2-sinθ2y,sinθ2l2+cosθ2y),即,在XOY中的坐标为(Px,Px),其中
(1)
则末端P点的速度的平方为
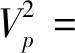
(2)
根据柔性臂杆2一侧约束,另一侧自由的结构特征,可将其等效为悬臂梁进行分析[7],由约束条件可知其频率方程为
coskl2coshkl2=-1
(3)
式中:l2为臂杆长度,则i阶的固有频率为
(4)
式中:ki为频率方程第i个解,E2为弹性模量;I2为材料横截面对弯曲中性轴的惯性矩;ρ2为材料密度;A2为截面面积。
对应i阶频率的模态振型函数为[8]
Zi(x)=cosh(kix)-cos(kix)-
(5)
关节转轴1的动能为
(6)
关节转轴2的动能为
(7)
杆1的动能为
(8)
杆1末端关节处动能为
(9)
杆2的动能为
(10)
式中:Vx为杆2距关节x处的位置的速度,公式中两个积分分别用a、b代替
(11)
系统的势能为
(12)
(13)
其中,L=T1+T2+T3+T4+T5-V。
代入对应公式,并化简得
(14)
利用Matlab软件中的Simulink仿真程序对上述模型进行数值仿真。设定臂杆长度l1= 0.2m、l2= 0.3m, 截面尺寸分别为A1= 9×10-5m2、A2= 1.5×10-5m2,材料密度分别为ρ1=7.8×103kg/m3、ρ2=7.9×103kg/m3,弹性模量分别为E1=2.06×1011N/m2、E2= 1.95×1011N/m2,则其对弯曲中心轴的惯性矩分别为I1= 1.69×10-9m4、I2= 1.25×10-12m4;O、O2关节处电机转子转动惯量分别为J1= 4.5×10-5kg·m2、J2= 5.5×10-6kg·m2,加载力矩分别为τ1= 2.3N·m、τ2= 0.46N·m。
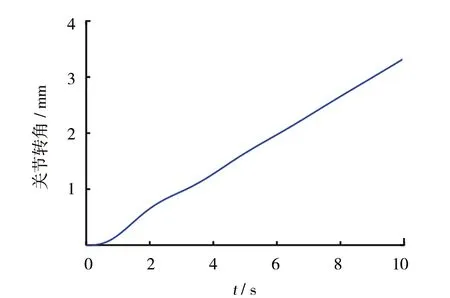
图2 刚性臂杆关节转角曲线
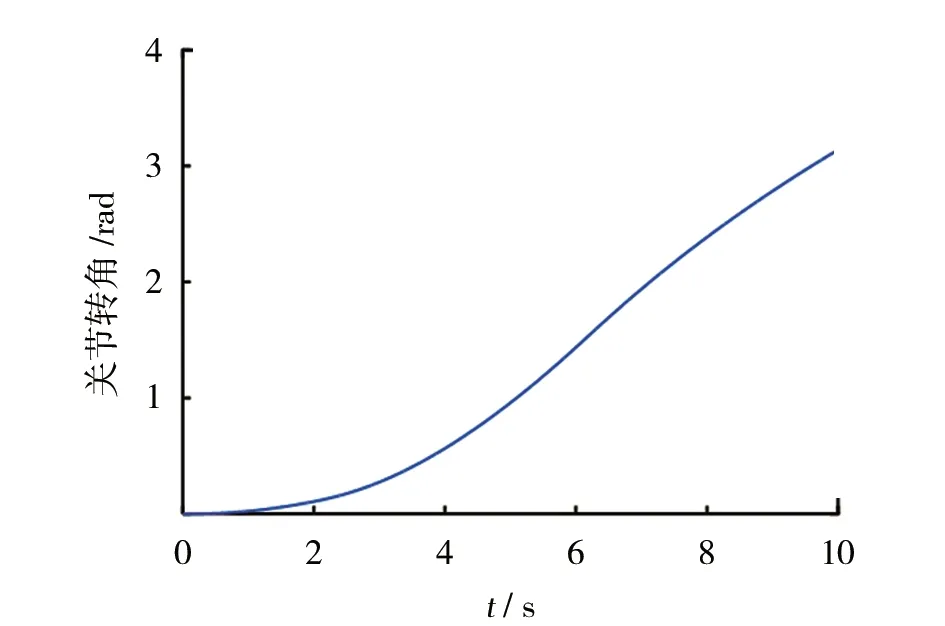
图3 柔性臂杆关节转角曲线
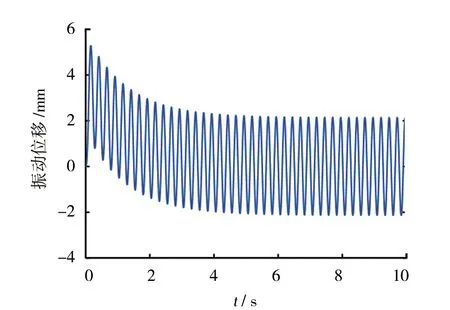
图4 末端振动位移曲线
从仿真结果可以看出,除开始阶段的轻微波动外,刚性臂杆1的转角曲线斜率基本不变;相对而言,柔性臂杆2的转角曲线斜率变化较大;末端振动位移曲线主体是幅值2mm、频率4Hz左右的正弦曲线,但在开始阶段出现将近3mm的整体明显偏差,在3s左右趋于平稳。
上述建模过程均在关节为刚性转动的前提之下进行,假定了作用在机械臂上的力矩等于驱动力臂,然而,关节柔性作为机械臂振动的主要原因,是不可忽略的[9]。为了提高模型精度,确保仿真与实际情况相符,需要在模型的建立中考虑关节柔性的影响,为后续的振动控制奠定更可靠的理论基础。
1.2 考虑关节柔性的模型改进
关节柔性是指柔性机械臂关节处的驱动电机转动时,电机转子带动的电机轴会产生扭转振动,而电机轴再带动被驱动件,也就是机械臂臂杆,传递过程中存在阻尼。本文从模型精确度以及运算复杂度出发,选择线性转子-扭簧系统模型,该模型利用扭簧表示关节处电机与驱动件之间的传动关系,忽略驱动电机内部动力结构与传动装置,只考虑关节的输出运动参数与驱动力矩之间的关系。

图5 柔性关节模型示意图
如图5所示,分别在电机转子与壳体上建立坐标系qm和qs,θm为电机驱动下臂杆的实际转动角度,θs为柔性机械臂关节处电机输出角度,即电机与搭载电机的臂杆关节壳体的相对转动角度,而电机与关节所受力矩的关系为
(15)
式中:τm为电机受到的力矩,τ为电机产生的驱动力矩,τs为关节受到的力矩,K表示扭簧的非线性扭转刚度,可利用关节所受扭矩和转角的实验测量数据进行拟合求得。
考虑上述关节柔性问题,结合已有模型对其进行优化。首先仿真模拟出关节柔性参数,假定关节转动响应的实际转动角度曲线如图6所示。
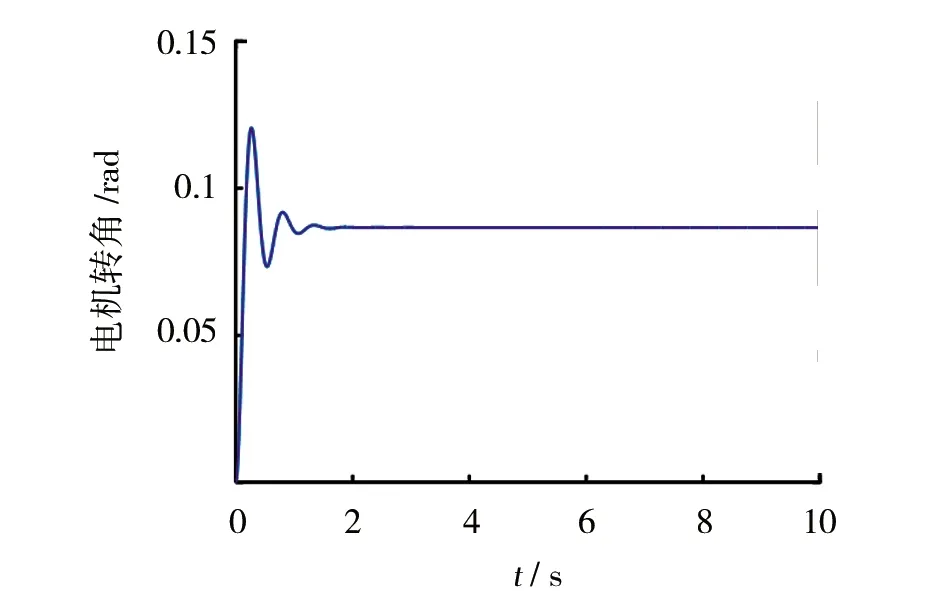
图6 关节实际转角响应
采用此属性下的关节力矩传动关系,将上节模型的相关力矩变量进行更改并仿真,其余参数、初始条件以及仿真时间均不变,得到考虑关节柔性的两关节柔性机械臂的关节转角及末端振动曲线,如图7~图9所示。
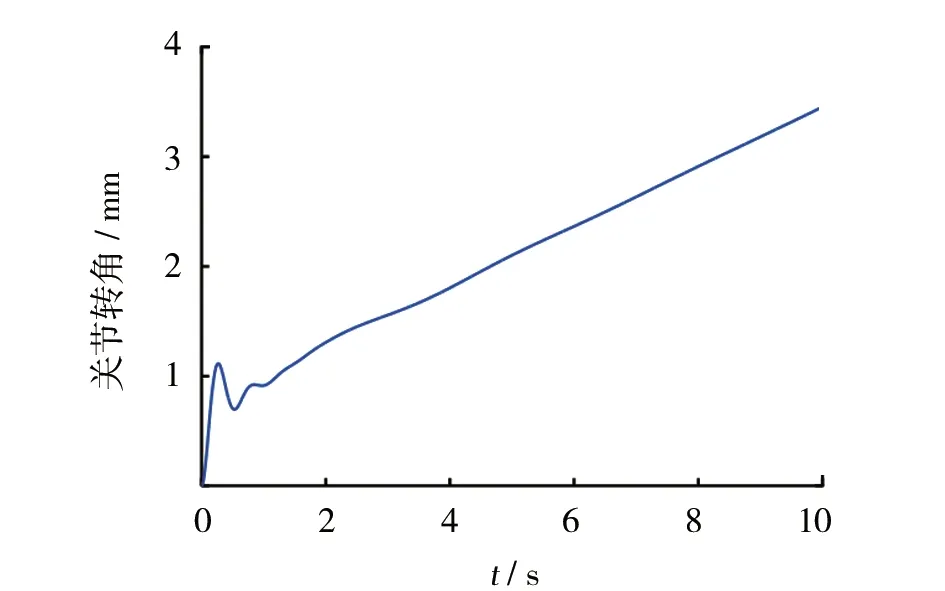
图7 考虑关节柔性的刚性臂杆转角曲线
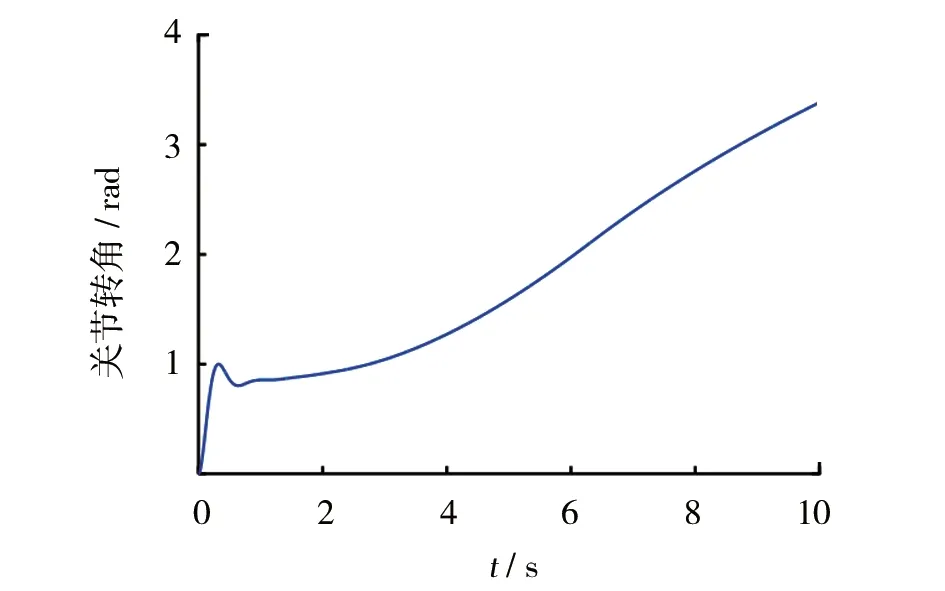
图8 考虑关节柔性的柔性臂杆转角曲线

图9 考虑关节柔性的末端振动位移曲线
从仿真结果可以看出,考虑关节柔性之后,两个关节转角曲线在原曲线趋势的基础上,均在开始阶段出现了明显的震荡波动,相比于柔性臂杆2,刚性臂杆1的波动更明显;而末端振动曲线在关节柔性影响下的改变更大,在开始阶段出现了将近6mm的大幅值曲线震荡,且曲线为多频率波形叠加状态,然后逐渐衰减,在5s左右变为幅值2mm、频率4Hz左右的稳定正弦曲线。
根据仿真结果并结合关节柔性模型,可分析得:由于考虑了关节柔性,在启动阶段关节转角响应电机驱动时,关节转角会出现大幅度的摆动,然后摆动幅度逐渐衰减直至平稳运转,而且此情况对刚性臂杆转角的影响较大;末端振动位移方面,同样是由于启动阶段关节处的摆动,才出现了振动,所以出现了开始阶段波形为不同频率波形叠加,而一段时间后恢复单一频率波形的情况。上述结果与分析说明了关节柔性会直接影响两关节柔性机械臂的仿真结果,在对其模型建立时是否考虑关节柔性十分必要。
2 基于正交试验的柔性臂振动测量
2.1 实验装置
为了验证模型的准确性,并进一步探究柔性机械臂的振动特性,设计基于压电材料的柔性机械臂振动测量系统。选定长300mm,宽15mm,厚1mm的不锈钢材料作为柔性臂杆;选定长200mm,宽15mm,厚6mm的碳钢作为刚性臂杆;考虑速度控制和系统成本,选择步进电机作为驱动电机;根据臂杆质量以及转动速度,选择输出力矩为2.3N·m的57步进电机(下文简述为大电机)作为连接底座与刚性臂杆关节的驱动电机;选择输出力矩为0.46N·m的42步进电机(下文简述为小电机)作为连接刚性臂杆与柔性臂杆关节的驱动电机,并为两电机配备普菲德生产的DM542驱动器及型号为KH-01的控制器。
根据柔性机械臂尺寸,选择22mm×19.5mm的矩形PZT压电陶瓷单晶片作为传感片, 极板面积为18mm×18mm,压电片两表面极板之间的距离d=0.12mm;压电常数d31=220×10-12C/N。为了对其一阶模态情况下的振动情况进行准确测量,在距离柔性臂杆固定处30mm的位置进行压电片的粘贴[10],装置示意图如图10所示。

图10 机械臂实物图
选择NI公司的USB-6003数据采集卡作为采集器件,在LabVIEW平台上编写程序控制采集卡进行采集。查阅相关资料可知,除特殊要求外,一般的柔性机械臂的角速度在10(°)/s~30(°)/s之间,为贴近工程实际,选择20(°)/s作为角速度进行研究;而步进电机的转速由细分、驱动脉冲频率以及步距角共同决定,具体关系为
ω=fqθb/nx
(16)
式中:ω为转动角速度,单位为(°)·s-1;fq为电机驱动脉冲频率,即每秒输出的脉冲数;θb为电机步距角,nx为电机细分数。电机细分数一般为2的倍数,为保证基本转动精度要求,细分一般设定为32、64、128等高细分。
从上述参数设置可知,存在各电机转速、各电机细分以及各电机驱动频率等大量变量,若一一对应组合,会产生大量的实验组数,逐一试验的话,耗时巨大,且意义不大。针对上述情况,拟采用正交试验的方法设计试验方案,在进行尽可能少的实验次数的前提下,探究尽可能多的影响振动特性的参数变量,减少工作量。
2.2 正交试验设计
正交试验是研究多重影响参数的一种快速、便捷且有效的实验设计方法。为了设计探究刚柔耦合下的柔性机械臂振动特性的正交试验方案,首先需要确定试验中的参数变量以及各变量可设定的参数值。根据上节机械臂设置情况可知,每次测量给定总的角速度之后,还需要设定电机速度、电机细分以及电机驱动频率,具体为刚性臂杆的转动角速度ω1、大电机细分nx1、驱动频率fq1、柔性臂杆的转动角速度ω2、小电机细分nx2以及驱动频率fq2。上述6个变量为待设定参数,但根据公式(16)可知,角速度、细分和驱动脉冲三者中已知两个便可确定另外一个量,所以,待定参数为4个;此外,为了保证实验组的对照性,并使实验更贴近实际,同上节,规定总的角速度为20(°)/s,此时,大小电机的角速度确定其中一个电机的角速度,便可知另一个电机的角速度,综上所述,待定参数数量为3个,也就是3个因素。由于细分的有限种类以及总角速度的确定,在上述六个参数中,选定大小电机的细分数nx1、nx2作为待定参数,并在大小电机角速度中,选定小电机角速度ω2为待定参数。
根据步进电机特性可知, 过低的细分在电机运转时会产生过大的颤振和抖动,所以实际应用中不常采用过低的细分设置,据此,选取32、64、128作为nx1、nx2因素的三个水平。 根据20(°)/s的总角速度并考虑实验对照性, 选取5(°)/s、10(°)/s、15(°)/s作为ω2因素的三个水平,选择L9正交试验表进行试验方案设计,具体如表1所示。
3 基于小波变换的时频谱分析
3.1 时域结果
测量的初始条件为:将柔性臂杆转动至刚性臂杆的直线延长线位置,作为初始位置;设定两步进电机转动方向一致;同时启动大小电机,采样时间设为10s,采样率设为1k;按照表1参数分别设置并进行9组实验,得到9组原始时域信号;由于电机电源的干扰,需要对原始信号进行去噪,利用Matlab进行低通滤波处理,截止频率选择45Hz,得到最终结果如图11所示。
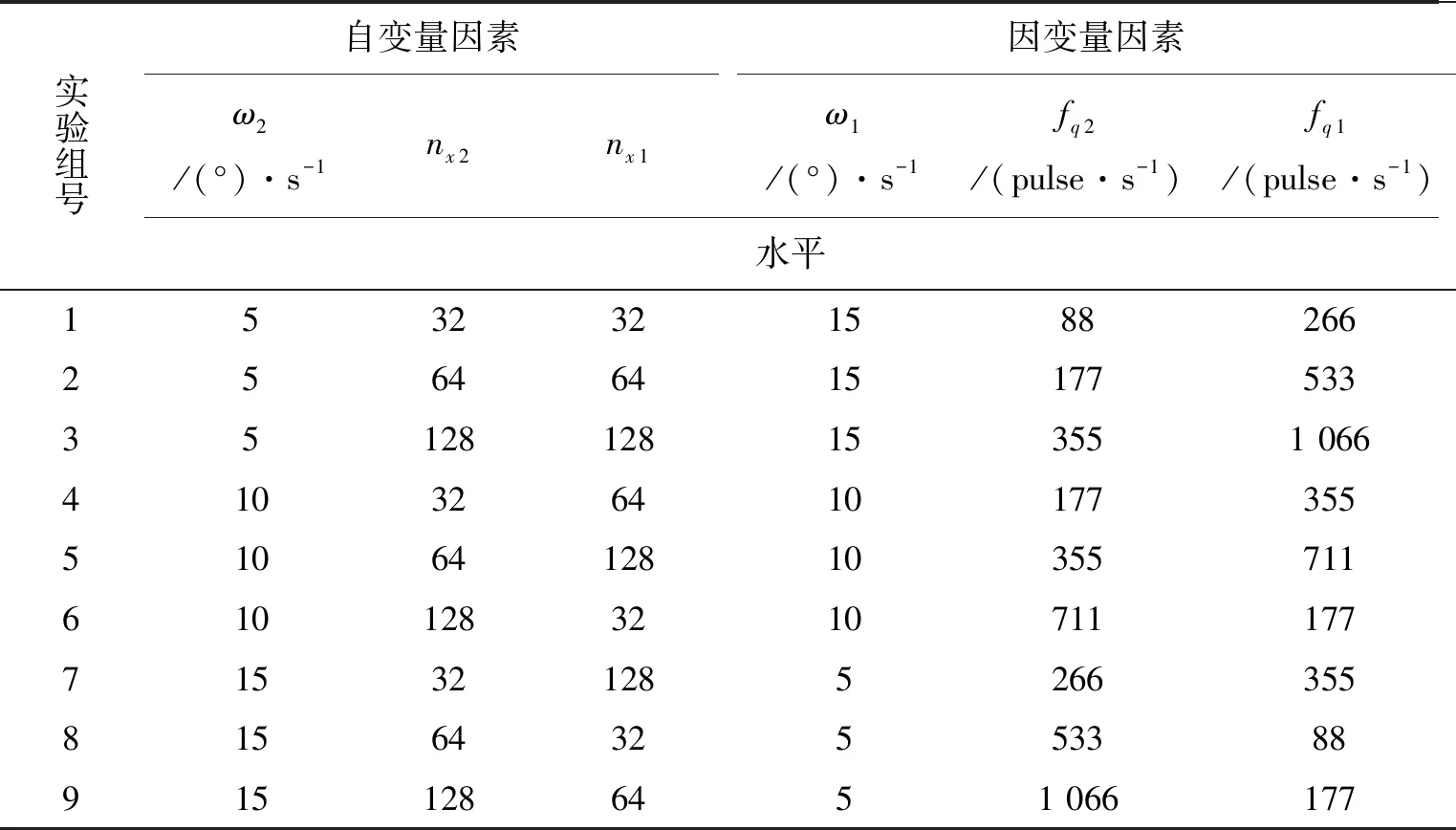
表1 正交试验表

(a) 第1、2、3组结果
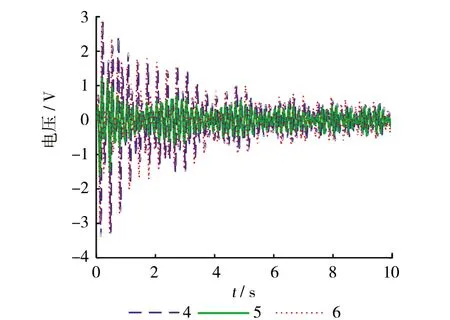
(b) 第4、5、6组结果
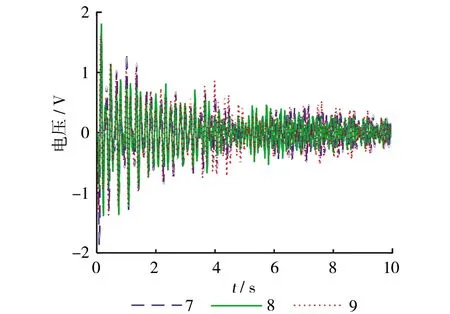
(c) 第7、8、9组结果图11 第1~9组测量结果
从图11从可以看出,9组情况下的柔性机械臂振动,均呈现出先大幅值震荡然后逐渐衰减至稳定小幅值振动的趋势,与图9考虑关节柔性的振动仿真曲线趋势相同,说明了考虑关节柔性建立的模型较为准确,能够仿真柔性机械臂的实际振动情况。除此之外,从图11中还可看出,三组不同设置下的振动,虽然总体趋势是一致的,但是振动幅值、稳定时间以及衰减时间等都是不同的。为探究不同参数设置下的刚柔耦合机械臂振动特征,需要进一步对信号进行处理,去探究影响其振动特性的参数量是哪些,以及它们之间的影响关系。
3.2 小波变换及分析
小波分析是时频分析方法的一种,不仅能得到信号的频率组成,还可以得到不同频率在不同时间下的强度大小。小波分析的时频分辨能力与其频率分解尺度有关,并且,低频信号成分的时间分辨能力较强,高频信号成分的频率分辨能力强[12]。根据测量信号的频谱图可知,测量信号属于低频信号,为了在保证时间分辨能力的同时提高频率分辨能力,采用f/2048的频率分解尺度,对信号进行小波变换,得到的时频谱结果如图12所示。

(a)第1、2、3组时频谱结果
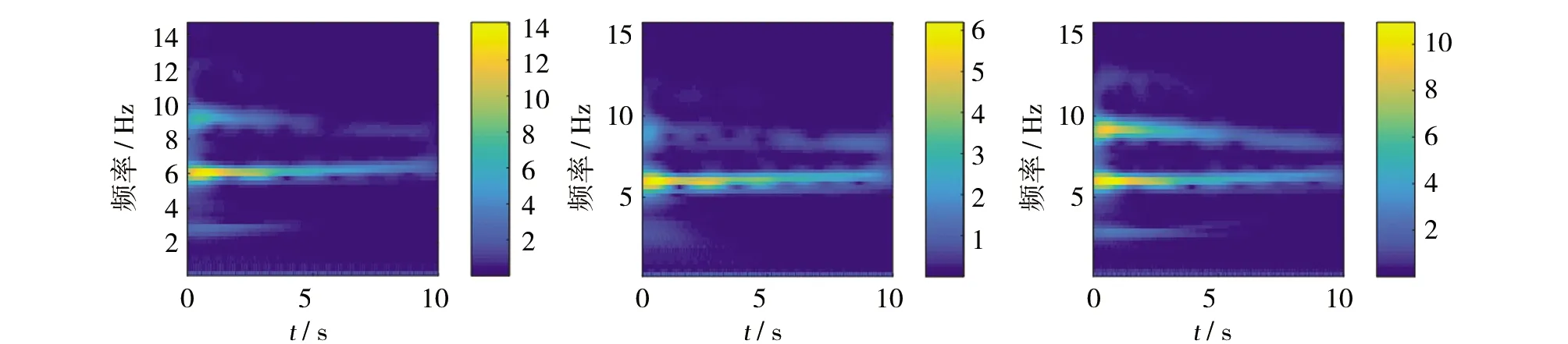
(b)第4、5、6组时频谱结果
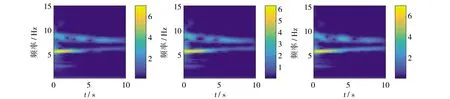
(c)第7、8、9组时频谱结果图12 第1~9组时频谱结果
如图12时频谱结果所示,其中横坐标为时间,纵坐标为频率,谱中每一点的颜色由该点对应时刻下,对应频率的强度确定,颜色亮暗程度与信号强度的关系如时频谱右侧的能量条所示,信号的强度大小与振动幅值相关,强度越大,振动幅值就越大。从时频谱中可以看出,每幅谱在6Hz、9Hz左右处均明显存在两条高强度区域频带,且在前几秒处,存在由大强度逐渐衰减的衰减段;在后几秒处,存在强度变化较小的平稳段。
为更具体地对这两种频率信号成分进行分析,采用类间方差确定衰减段与平稳段的分界点。设每条频带区域内t时刻fHz信号的强度为B(t,f),其中,0s (17) 衰减段、平稳段内的强度均值为 (18) 分界时间为t0时的类间方差为 (19) 将t0遍历0~10,定义得到最大类间方差的t0为最终分界时间T,即 (20) 确定分界时间之后,定义衰减段中的最大强度B1、平稳段的强度平均值B2为振动特征、最大强度B1对应的频率F为频带频率。 按照上述定义,提取每幅谱中每条频带的衰减段最大强度、平稳段强度以及两阶段的转换时间点作为振动特征,具体值如表2所示,结果保留两位小数。 表2 第1~9组振动特征值 从表2可以看出,频带的频率基本固定在5.86Hz和9.03Hz,并且,除第3组外,5.86Hz频带的衰减段最大强度均大于9.03Hz的强度,由此说明振动信号由5.86Hz、9.03Hz成分组成,且5.86Hz为主成分;观察分界时间,可看出5.86Hz、9.03Hz频带衰减段基本在4~5s、2~3s结束,且1~9组整体趋势从高逐渐减小,结合表1可判断电机转速对进入平稳阶段的时间有一定影响,并且小电机的转速越大、或者大电机的转速越小,振动进入平稳阶段的时间越早。 此外,两频带的衰减段最大强度变化与平稳段最大强度变化基本同步,说明细分和转速对其作用影响规律基本相同,结合表1对其影响进行分析。对比1、2、3组结果可看出,两电机细分相同时,随着电机细分的增大,两频带衰减段、平稳段的强度均有所下降;而大电机为128细分的3、5、7组结果,相对于小电机为128细分的3、6、9组结果,其衰减段最大强度较小;说明电机细分越小,引起的振动强度就越大,并且大电机细分的影响较大。对比1~3、4~6、7~9组结果可看出,小电机转速越小,也就是大电机转速越大,引起的振动强度越大。观察表2,振动强度最小的为第3组,其细分最小,但大电机转速较大;强度最大为第1组,其细分最大,但大电机转速同样较大,说明相比于转速的影响,电机细分对振动强度的影响较大。 本文采用拉格朗日方程及假定模态法对刚柔两关节机械臂进行了建模,并考虑关节柔性对模型进行了优化,利用实验验证了考虑关节柔性的必要性。选取臂杆转速以及电机细分配置作为因素设计正交试验,并对测量结果进行小波变换,探究了其振动特性;定义了衰减段强度等多个信号特征,通过对比多组结果,得到了不同因素对振动特性的影响关系,为机械臂配置提供了可靠的参考。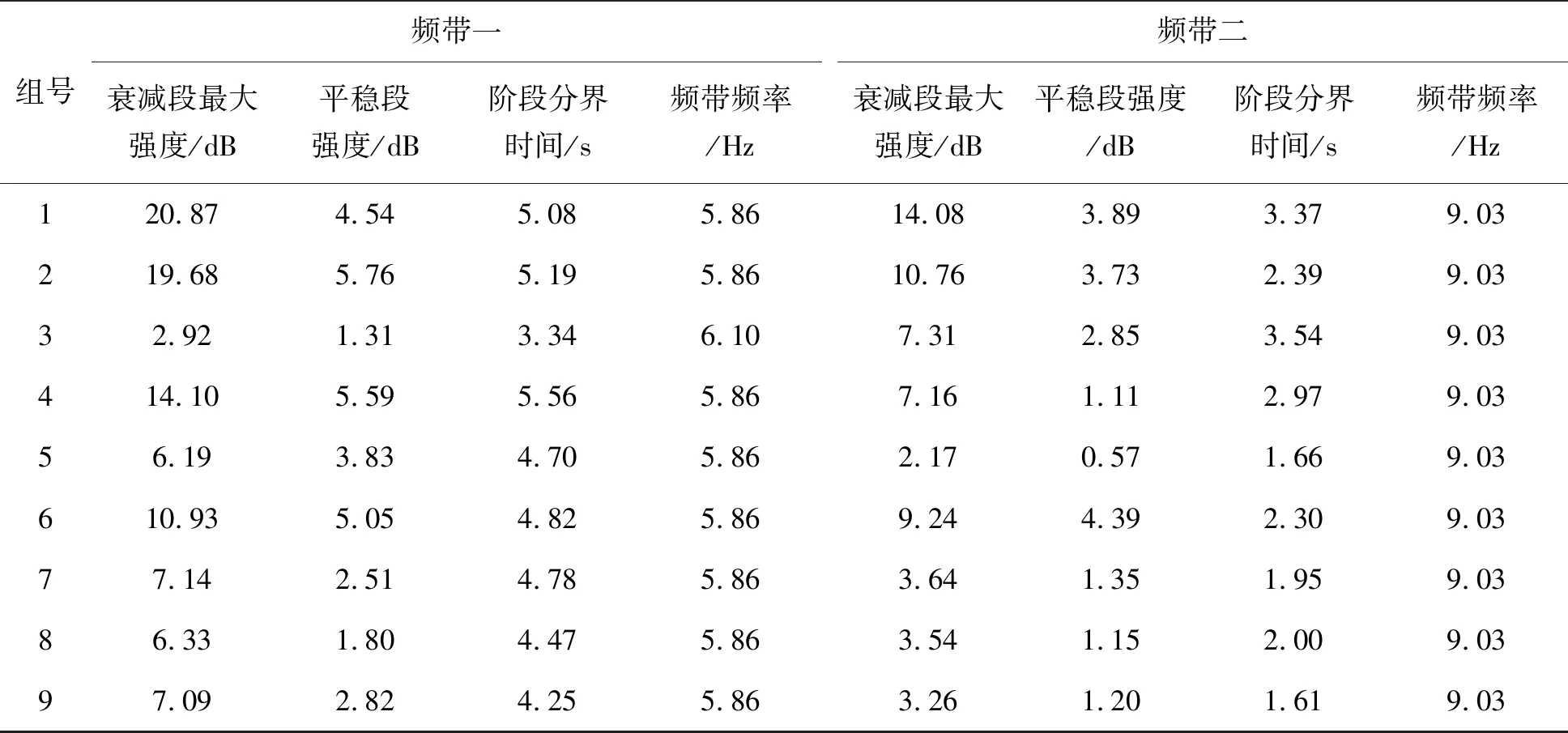
4 总结

