基于期望最大化的K-Means聚类算法
景 源,郝金山
(辽宁大学 信息学院,辽宁 沈阳 110036)
0 引言
在数据挖掘领域中,聚类技术是应用广泛且十分重要的技术.聚类分析已经应用在各种方面,比如其在机器学习,文本分类,图像处理,语音处理,模式识别等领域.
常见的聚类方法有模型方法,密度方法[1],网格方法[2],层次划分方法[3]和划分的方法.其中EM算法[4-10]属于模型方法.K-means算法[11-17]属于划分的方法.在这些方法中最著名的就是kmeans方法,kmeans方法具有简单,快速,有效等诸多优点,但它也有非常明显的不足.Kmeans算法过于依赖于初始聚类中心.
文献[8]中,提出一种基于稀疏约束非负矩阵分解的kmeans聚类方法,通过在在非负矩阵分解过程中对基矩阵列向量施加l1和l2范数稀疏约束,实现高维数据的低维表示,然后利用在低维数据聚类中性能良好的kmeans算法对稀疏降维后的数据进行聚类.该方法适合于高维数据,并有良好的性能.但缺点是需要消耗的时间较长.文献[9]中先根据类簇指标确定需要聚类的数k,之后采用基于密度的思想,首先将聚类样本分为核心点、边界点和孤立点,之后排除孤立点和边界点并取核心点的中心点作为k个聚类中心后再进行kmeans聚类.虽然算法比原始的kmeans算法准确率得到提高,但同样耗时较长,而且在已知k值的情况下,有可能出现k值对不上的情况.文献[10]通过定义的平均类间最大相似度指标值来确定最佳的k值,将所有数据点中密度较高的点作为备选聚类中心,将备选点中密度最大的两个点作为聚类中心进行初步聚类计算并更新当前聚类中心.根据平均类间最大相似度来决定是否添加新的聚类中心,结果表明该算法可以有效的提高聚类的精确性与稳定性,而且还能在一定程度上缩短聚类时间,但随着数据量的增大,特别是对高维数据而言,这些优势会极大的减弱.
针对以上出现的问题,本文提出一种新的初始化方法,用EM方法初始化k-means方法,代替传统意义上的随机初始化,让初始聚类中心离最终的聚类结果更近一些并且适合高维数据.
1 K-means算法
经典的k-means算法思想是随机选取k个数据点作为初始聚类中心,然后根据一定的距离算法(欧式距离)迭代计算聚类中心,每次计算类内平均值作为新的聚类中心,直到满足聚类要求,最后返回k个聚类中心和最终的蔟类.
K-means算法步骤:
1)从数据集A中随机选取k个数据对象作为初始聚类中心.
2)求每个数据点与初始聚类中心的距离.
3)根据距离,将每个数据点分配到距离其最近的聚类中心.
4)求每个类内平均值,作为每个蔟的新的聚类中心.
5)设置聚类迭代上限,或者准则函数.
6)判断,如果满足或者达到最大迭代次数,表示迭代结束,否则返回步骤2.
2 K-means算法的改进
2.1 初始聚类中心的选择
针对k-means算法中,初始聚类中心对最终聚类结果影响较大,但初始聚类中心又是随机的,不确定性太大,对于这种问题,把EM算法与k-means算法相结合,用EM算法来求解k-means算法的初始聚类中心.
EM算法的好处在于它可以根据已知数据和数据分布模型得到每一个样本属于哪一个分布和模型分布的参数.为了对高纬数据进行聚类,考虑到自然界中大部分数据都符合高斯分布,所以这里采用的是多维高斯分布模型,因为这里用的是向量,所以需要考虑向量与向量之间的关系.
多维向量的高斯概率密度函数是:
(1)
假设要把数据分成k类,每类分别服从多维高斯分布.让原数据以列向量的形式存在.
第t类的高斯概率密度函数是:
EM算法中存在如下Jensen不等式:
隐含变量z即为所对应的类别,Qi是条件概率,在这里可以用概率密度函数代替,表示属于对应变量z的概率.隐含变量z即为所对应的类别就是要找到k-means初始聚类的聚类所对应的种类.未知参数为θ={u,Y},u为均值,Y为协方差矩阵,应用的EM算法的具体流程如下:
1)对θ={u,Y}赋初值,不同的类赋不同的初值.
2)根据θ的值求:
3)根据Qi的值确定分布的类型,找到Qi最大的值所对应的种类c,若服从第一类的分布模型,则把第一类的概率密度函数代入,若服从第二类的分布模型,则把第二类的概率密度函数带入.若k的值大于2,则找到Qi所对应种类的模型.
(2)
EM算法的E步:初始化θt或者根据更新后θt的求Qti代入Lt(x).
M步:让Lt(x)最大化,即分别对Lt(x)求导,让导数为零,如让L1(x)分别对,Y1,u1求导数,让导数为零,下面为具体的推导过程.
先简化公式参数的似然函数如下所示,求导过程中Q1i(z)是个常数可以被省略
n为维数,构造公式R为:
则L1(x)求导可以简化为R求导,分别对u1求导和Y1求导,当导数为零可得到,
(3)
(4)
根据公式(3)和公式(4)求得均值和协方差矩阵:
公式中的n1是指服从第1类的数据的数量,如此就求出了第一类概率模型参数的值,之后每一类的概率模型参数的值同理可求,最后得到的参数值代入E步,依次在E步和M 步之间循环,直到参数不再变化为止,如此就求出了每个模型的参数.知道了每个数据的隐含类别Z,根据隐含类别,将数据归类,求每个类别的均值,作为k-means算法的初始值.这样就是把EM算法用于k-means算法初始聚类中心的选择.
2.2 距离公式
一般k-means算法所采用的距离公式多为传统的欧式距离,对于高维数据而言,欧式距离的性能收到限制,特别是不同维度的差异较大时,故本文采用一种新的公式作为距离算法,以两个列向量的比值为基础,作为两个数据的距离度量.
(5)
其中a和b可以看出分别为两个维度为n的列向量,dab值越小表示距离越近.
以下是k-means算法的改进具体流程:
1)从已有的数据集中选取一定量的数据进行一次递归.
2)在递归过程中采用EM算法计算出初始聚类中心,并用于计算出在第一次递归中的聚类计算.
3)利用邻近原则和提出的距离算法,根据距离的远近分配到就最近的簇中.
4)根据计算,得到每个簇中的平均值作为新的聚类中心.
5)判断聚类函数是否收敛,如果收敛,则返回聚类结果.若不收敛,则转到步骤(3),继续计算,直到收敛为止.
6)把递归回的结果,作为全部数据的初始聚类中心,以相同的原理利用步骤(3)至步骤(5),并得到最终的聚类结果并返回.
通过部分数据递归EM算法,得到的聚类结果作为真正的初始聚类中心,从而让初始聚类中心离最终理想的聚类结果更近一些,提升算法准确性.
3 仿真与实验
3.1 实验描述
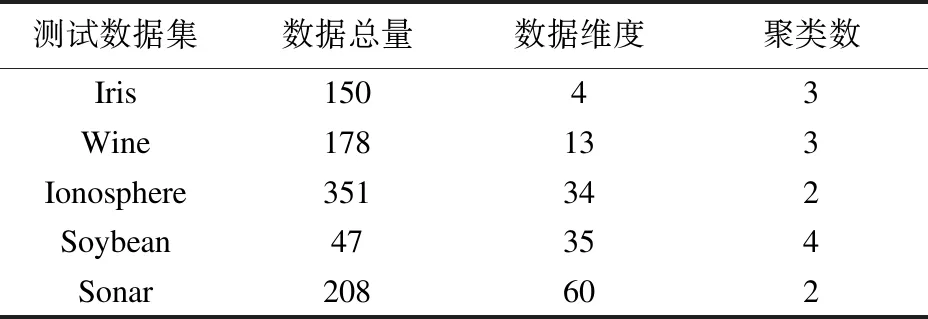
表1 数据集分布
为了验证算法的准确性和稳定性,本文从UCI数据集中选取Iris,wine,Ionosphere,Soybean,Sonar等5个经典数据集进行测试.UCI数据集是经典的用于测试机器学习和数据挖据的数据集,其中的数据有明确的分类.关于分类准确率问题上,在数据集上分别运行k-means算法,NMFS-K算法[8]和本文算法各10次,每次迭代次数不超过100次,随后取均值进行比较,其中递归时取其中1/4的数据.数据集的分布如表1所示.
3.2 实验描述
基于表1所示的UCI数据集,对k-means算法,NMFS-K算法和本文算法的聚类结果进行对比分析,用分类准确率对结果进行评价,分类准确率按如下公式:
其中ai为每个类中正确聚类的数据个数,k为聚类个数,n为数据总数,CA的值越高聚类的效果越好,实验所得的CA值如表2所示:
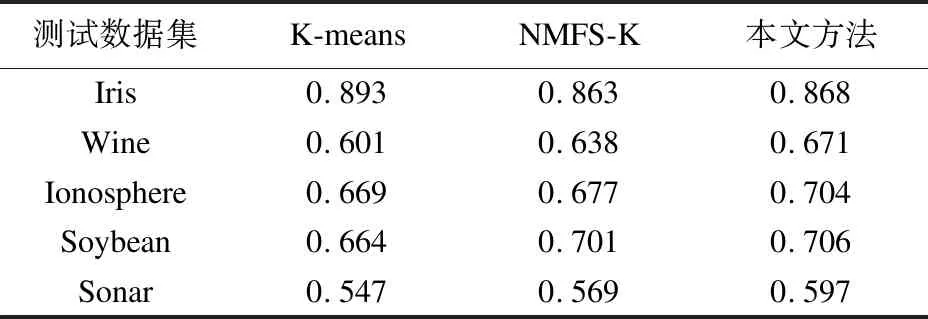
表2 聚类的CA值
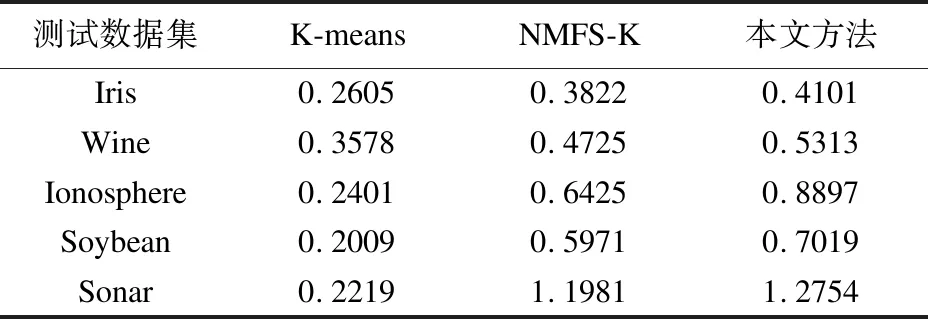
表3 运行时间(t/s)
从表2可以看出传统算法相对于高维和数据量大的数据而言,聚类的效果不是很好,NMFS-K算法相比于传统的算法,除了在低维数据上表现不好外,其他相比于传统算法要好一些,本文方法虽然同样在低维数据表现不好,但在高维数据上要比前两种方法要更好上一些.故本文方法比较适合于高维数据.
为了从时间上对比分析算法的效率,记录了各个数据集的运行时间.如表3所示,本文方法相比于前两种方法而言,需要消耗更多的时间.
4 总结
针对高维数据的数据集,提出了聚类算法改进,把EM算法和k-means算法相结合,使EM算法用于递归中来确定初始聚类中心,让初始聚类中心离最终聚类结果更近一些.并为了更好地提升算法的准确性,提出一种新的距离算法.通过实验证明,提高了算法的准确性,并且适合于高维的大数据量的处理,证明了算法的有效性,但是缺点是所需计算的时间延长,需要更好的改进.

