新人教版九年级上册第二十四章圆教学设计 24.1.1 圆

凡责艳

一、教学目标及其重、难点

（一）教学目标

1、知识与技能

探索圆的两种定义，理解并掌握弧、弦、优弧、劣弧、半圆等基本概念，能够从图形中识别。

2、过程与方法

（1）体会圆的不同定义方法，感受圆和实际生活的联系。

（2）培养学生把实际问题转化为数学问题的能力。

3、情感、态度与价值观

在解决问题过程中使学生体会数学知识在生活中的普遍性。

（二）教学重点

圆的有关概念。

（三）教学难点

理解圆的概念的形成过程和圆的集合性定义。

二、教学过程设计

（一）情境引入

一些学生做投圈游戏，他们呈“一”字排开。这样的队形对每一人都公平吗？如果不公平，你认为他们应排成什么样的队形才公平？

答：不公平，应该站成圆形

（设计意图：打破常规生活中的圆形介绍， 由同学们感兴趣的游戏引入，吸引学生注意;其次学生在思考游戏不公平的同时，回答应该站成圆形，使每一个学生到投心的距离相等引入圆，自然切入本节课题：24.1.1 圆 ）

（二）探究新知

1、圆的概念

问题1：观察画圆的过程（如图1），你能说出圆是如何画出来的吗？（多媒体PPT动画演示）

（设计意图：通过PPT动态演示，让学生真切感知和回忆圆的形成。同时让学生自己陈述画圆过程，加深对圆动态定义的理解）

（1）圆的定义（ 动态定义）

在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。点O为圆心的圆，记作“⊙O”，读作“圆O”。（画完圆，就说出O点叫圆心，OA叫半径;同时引出初中新概念圆心也叫定点，半径也叫定长）

问题2：动动手，在一张纸上1.以1cm为半径能画几个圆？（答：无数个）

2.以已知点O为圆心能画几个圆？（答：无数个）

（设计意图：本节课属于圆的概念课，分别以半径长度确定和圆心位置确定让学生动手画圆，增加学生的动手能力。同时通过类比，让学生发现画一个确定的圆需要圆心和半径两个要素）

问题3：根据上述画圆的过程（如图2），小组讨论完成以下填空：（按班级分成5个小组，小组讨论1.5min）

①确定一个圆的要素：圆心和半徑，其中圆心确定其位置;半径确定其大小。（圆心也叫定点，半径也叫定长）

②圆上各点到定点（圆心O）的距离都等于 定长r ;

③到定点的距离等于定长的点都在同一个圆上。

（设计意图：圆的静态定义是本节课的难点，如果通过老师直接陈述概念，学生很难理解。根据学生动手画圆过程，以小组讨论方式总结出圆的静态定义，加深学生对新知的理解和掌握）

（2）圆的定义（ 静态 定义）

到定点O的距离等于 定长r的所有点的集合。

（再在圆上选一些点，就会发现其实圆是由点构成的）

（3）圆的基本性质：同圆的半径 相等

例1 如图3，矩形ABCD的对角线AC、BD相交于点O.求证：A、B、C、D四个点在以点O为圆心的同一个圆上.

证明：∵四边形ABCD为矩形

∴

∴

∴A、B、C、D四个点在以点O为圆心的同一个圆上.

（设计意图：证明此题学生可以及时巩固所学知识，使本节课的教学重难点得到进一步落实。其次让学生板演，老师可以观察学生的掌握情况并做进一步强调和调整）

2、与圆有关的概念

问题1：请同学们找出上图3中的所有线段，观察这些线段的两个端点的位置有什么区别？（请学生接龙回答）

（设计意图：直接用上述图作为例子，引出与圆有关的概念，既增强课程连贯性，又不会唐突，使课程环环相扣）

（1）弦

连接圆上任意两点的 线段 叫做弦.如图3中的AB.

图3中的弦还有 BC、DC、AD、AC、BD

问题2：上述所有弦中，大家找一找哪些线段又存在特殊性？（答：发现AC、BD过圆心）

经过圆心的弦叫做直径（如图中的AC）

观察图中（备用图如下）弦BD与BC有怎样的大小关系？（答：BD>BC，即直径大于不是直径的弦，直径是最长的弦）

注意：

①弦和直径都是 线段 .

②直径是 弦 ，是圆中 最长 的弦，但弦 不一定 是直径.

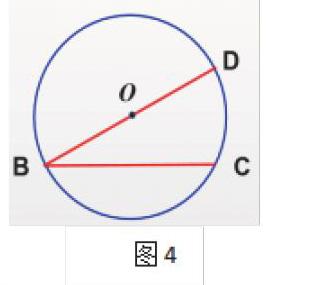
问题3：把上图中较多的线段去掉（如图4），留下两条BD、BC，这些线段的端点把圆分成了几部分？

（答：线段的两个端点把圆分成了两部分）

（设计意图：去掉多余线段，留下典型两条，便于学生观察，引出弧的概念）

（2）弧

圆上任意两点间的 部分 叫做圆弧，简称弧.如图4中以B，D为端点的弧记作 ，读作“圆弧BD”或“弧BD”.

注：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做 半圆 .

大于半圆的弧叫做优弧，用三个大写字母表示.如图4中的   ;

小于半圆的弧叫做 劣弧 ，用两个大写字母表示.如图4中的

3、等圆、等弧概念

（1）等圆

如图5，图中两个不同位置的圆经过移动之后，两个圆能够重合

（多媒体PPT动画移动演示）

能够 重合 的两个圆叫做等圆.

推出：等圆是两个半径相等的圆.

（2）等弧

如图6，在⊙O中弧AB经过旋转能够与弧CD完全重合

（多媒体PPT动画移动演示）

在同圆或等圆中，能够 完全重合 的弧叫做等弧

想一想，长度相等的弧是等弧吗？（答：不是）

（设计意图：等弧概念学生易混淆，较难理解，用实物展示，便于学生观察并很快得出结论，加深印象）

（三）随堂练习

1. 判断下列说法的正误.

（1）弦是直径;（×）   （2）过圆心的线段是直径; （×）

（3）半圆是弧; （√）   （4）過圆心的直线是直径;（×）

（5）直径是最长的弦;（√）   （6）半圆是最长的弧;（×）

（7）长度相等的弧是等弧.（×）  （8）同心圆也是等圆.（×）

2.如图7，点B、O、C和点A、O、D分别在同一条直线上，则图中有（ B ）条弦.

A.2 B.3 C.4 D.5

（设计意图：针对本节新课，选择针对性习题训练，加深学生对圆定义以及与圆有关概念的区分与理解，便于老师了解学生的掌握情况，并在总结中加以强调和落实）

（四）课堂小结

（设计意图：本节课属于概念课，知识较为零散，形成知识框架体系，便于学生把握。课堂小结一方面让学生回顾自己的学习过程，加强反思，提炼过程;另一方让老师及时了解学生掌握情况，便于教学反思）

（五）随堂检测

1.以点O为圆心作圆，可以作（  D ）

A.1个 B.2个 C.3个  D.无数个

2、如图8，图中的弦共有（ B ）

A.1条 B.2条   C.3条  D.4条

3、如图9，已知AB是⊙O的直径，点C在⊙O上，∠C=15°，则∠BOC的度数为（ B ）

A.15°   B.30°  C.45°    D.60°

4、下列说法：①圆的大小是由半径确定的;②直径是弦;

③半圆是弧，弧也是半径;④半径相等的两个圆是等圆.

其中正确的说法有（ A ）

A.①②④ B.①③④  C.②③④  D.③④

（设计意图：检测学生新知掌握情况，方便老师教学反思，并做下一节课课堂设计的依据）