判断,不止于“初见”
2020-06-27 04:20张丽琴
河北教育(教学版) 2020年4期
○张丽琴
在《分数的初步认识》单元整理和复习时,课本中有这样一道习题:
下面的分数能表示图中的涂色部分吗?


学生一致认为:不能。
生:虽然取了1份,但没有平均分成3份。所以不能用分数表示。
显然,学生对分数概念的关键——“平均分”已经理解,能正确判断与表达。但我并没有就此停止,而是进行了下面的尝试。
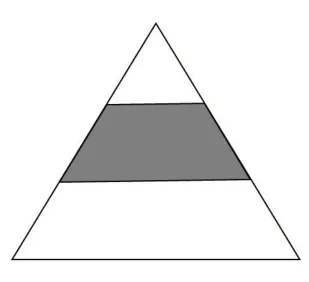
多数学生脱口而出:没有平均分,也不能。
师:验证出来才令人信服!可以画一画、分一分,也可以剪一剪、拼一拼,看有没有新发现。
展示一:把整个三角形平均分成9 个大小相等的小三角形,这9 个小三角形每3 个看成一份,涂色部分刚好占3份中的1份,可以用表示。
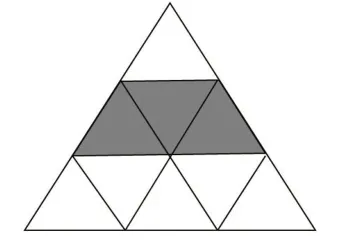
展示二:把整个三角形对折,平分成两个一样的三角形,再拼成一个长方形,涂色部分刚好是长方形的,也是整个三角形的。

生1:判断是不是分数时不能被表面的假象所蒙蔽。
生2:不能一看到各部分形状不同,就不假思索地认为不能用分数表示。
【教学思考】初步认识分数时,学生建构分数模型的难点之一在于:涂色部分形状不同,但大小相同时可以用同样的分数来表示。
第一,面对学生的错误认知,教师切忌越俎代庖。应让学生充分自主探索,发现知识的本质。这样,巩固了对平均分的理解,打开了对分数形态的认知;最后依托分享“战果”,提炼归纳出分数的本质属性。
第二,于交流中不断唤醒并挖掘学生思维的深度和广度。教学中,我没有蜻蜓点水般仅仅满足于学生判断是否正确,而是充分借助直观形象的操作活动,加深了学生对知识本质的理解和对分数概念的建构。让判断不止于“初见”,从“记忆”走向“理解”,帮助学生更深入地感悟数学,有效积淀数学素养。
猜你喜欢
小学生学习指导(高年级)(2020年6期)2020-07-07
数学小灵通(1-2年级)(2020年3期)2020-06-24
数学大王·低年级(2019年8期)2019-08-27
幼儿画刊(2018年11期)2018-12-03
幼儿画刊(2018年10期)2018-10-27
幼儿画刊(2018年9期)2018-09-26
幼儿画刊(2018年8期)2018-08-29
数学小灵通·3-4年级(2018年7期)2018-07-12
小学生学习指导(中年级)(2018年3期)2018-01-25
小天使·六年级语数英综合(2017年5期)2017-05-27

