经历策略形成过程,提升策略意识
蔡旅宇
教学内容:苏教版《义务教育教科书·数学》三级上册第71-73页例1和“想想做做”。
教学目标:
1.使学生在解决实际问题的过程中初步学会从条件出发展开思考,分析并解决相关问题。
2.使学生在解決实际问题过程的不断反思中,感受解决问题策略的价值,发展分析、归纳和简单推理的能力。
3.使学生进一步积累解决问题的经验,增强解决问题的策略意识,获得解决问题的成功体验,提高学好数学的信心。
教学重点:经历分析数量关系的过程,初步领悟从条件出发思考、分析并解决实际问题的策略。
教学难点:形成主动捕捉条件、积极从条件想起的策略意识。
教学过程:
一、创设情境,唤醒经验
(一)创设小猴摘桃的情境,出示题目: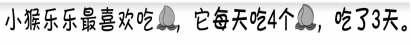
(二)引导学生根据条件提出问题并解答
设计说明:以小猴作为贯穿全课的主角,将整节课置于小猴摘桃的故事情境中,激发学生的学习兴趣。同时,根据两个有直接联系的条件提出问题的思维方法,是本课策略学习的生长点。引导学生进行练习,架起新旧知识之间的桥梁,让学生初步感受从条件出发寻求相关问题的过程,为进一步学习“从条件想起”的策略做一些准备和铺垫。
二、探索交流,形成策略
出示例1:小猴乐乐第一天摘了30个,以后每天都比前一天多摘5个。第三天摘了多少个?
(一)理解题目意思
交流:从题目中知道了什么条件,要求什么问题?
启发:你觉得哪个条件需要向大家解释一下?
指出:解决问题前,要像这样边读题目,边想意思。(板书:读题目想意思)
设计说明:从本质上看,“从条件想起”的策略是数量关系的顺向推理。运用这种策略的关键在于弄清题目的条件。这里把学习的主动权交给学生,引导他们用自己的语言解释题目中较难理解的条件。这样设计,为学生进一步展开从条件向问题推理的活动作准备。
(二)分析数量关系
提问:怎么根据第一天摘桃的个数得到第二天摘桃的个数?
指出:第一天摘的个数加5个就得到第二天的,就是这两天之间的关系。
提问:第二天和第三天之间的关系呢?
明确:理清了条件,我们也就找到了关系。(板书:理条件找关系)
设计说明:这个环节,仍然围绕关键条件展开分析,突出理解相邻两天之间摘桃个数的“关系”。这样浓墨重彩的处理,是为了避免学生忽略从条件出发思考数量关系而直接解题的现象,充分体现了从条件出发分析和解决问题的过程与方法,提升学生分析和解决问题的能力。
(三)确定解题思路
明确研究要求:
1.想想说说:先算什么,再算什么?在小组里交流。
2.写写算算:在学习单上列式解答。
学生探索交流。
指出:什么先算什么,再算什么,就是解题的步骤。按照步骤解决问题更加顺利。
(板书:定步骤解问题)
提问:分别根据哪两个条件依次求第二天、第三天摘了多少个的?
追问:“第二天摘了35个”这个条件哪来的呢?
形成板书: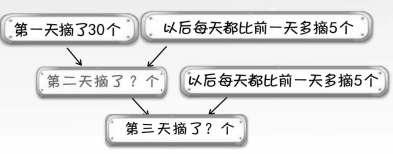
设计说明:这里没有追求多种解法,意在把例题的教学重点聚焦于策略的感悟与体验上,通过引导学生逐步完成由条件向问题的推理过程,借助结构图帮助学生直观理解分析数量关系的思考过程,帮助学生初步形成策略的表象,感受策略的价值。
(四)丰富解题经验
在例1后面,继续补充问题:第五天呢?
学生独立完成后交流解题思路。
追问:在求第二、三、四和第五天摘桃个数的时候,都用到了题目中的哪个条件?
指出:都用到了“以后每天都比前一天多摘5个”这个条件,说明关系相同,我们还可以列表来解答。相机出示表格:
启发:根据条件,你还能继续提出什么问题?
设计说明:将例题中的两个问题分开解决,由扶到放,又各有侧重。第一问重在体会解决问题的一般步骤,在解题过程中初步感受策略的形成过程。第二问重在引导他们自主经历解决问题的过程,并通过内省将获得的感性经验提升为理性认知,促进策略的主动建构和生成,形成对策略的初步体验。
(五)回顾反思
师生用三字口诀回顾解决问题的一般步骤:读题目,想意思,理条件,找关系定步骤,解问题。
小结:按照这样的步骤,我们解决了小猴摘桃的问题。像这样从两个有联系的条件出发,先求出一个问题,再一步步解决问题,是一种常用的解决问题的策略,叫从条件想起。
揭示课题
设计说明:解决问题的过程中,“方法”与“策略”如两条平行线同步推进且相互交融。方法是具体的,策略是从方法中提炼的认识。因此学生在解决问题之后,教师应引导他们对解决问题的方法和解决问题的过程进行回顾反思,内化理解,提升认识,使原本感性的经验得到适度的提升,逐步形成稳定的解题策略。
三、巩固练习,内化策略
(一)基础性练习
1.皮球弹起高度问题(“想想做做”第2题改编)
一个皮球从16米的高处落下,如果每次弹起的高度总是它下落高度的一半。皮球第几次弹起的高度和这个小朋友的身高(1米多一点)差不多?

2.根據条件,提出不同的问题(“想想做做”第1题改编)
追问:是根据哪两个有联系的条件提出问题?
根据学生的交流,完成如下的思维结构图: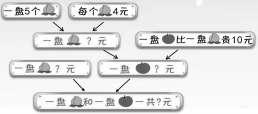
明确:根据有联系的条件,就能提出问题。
3.学生解决巩固练习第2题中的一问:“一盘苹果多少元?”
体会:用上从条件想起的策略,顺利解决这题。
(二)提高性练习
变式:把巩固练习第2题中的一盘苹果换成5个桃。
要求:根据给出的条件,作出不同的选择,提出并解决问题。
明确:“每盘5个桃”既和“每个桃4元”有联系,又和“有2盘”有联系。只要找到有联系的两个条件,就可以提出并解决问题。
四、畅谈收获,总结提升
设计说明:感悟在过程中产生和形成。学生对解决问题策略的感悟需要有具体的解题过程作支撑,需要以亲身经历的“做数学”的体验为根基,这样才能将“策略”逐渐内化。这里设计了不同层次的练习,以便学生有充分的感性积累和大量的实践体验。为了使练习与例题情境更为协调、统一,这组练习对教材习题略作了加工。将“想想做做”第2题,放在例题教学后练习,是因为这题与例题结构相似,且都有一个概括性强的条件,利用前一个计算结果和已知条件结合,逐步求出问题的结果,从而巩固“从条件想起”的完整体验。第2题让学生利用两个有联系的条件并连续提出新问题的过程,意在培养学生主动捕捉有联系的条件的能力,体会从条件出发进行分析和思考,逐步向问题推进的操作要领。提高性练习的两种解法,都是从有联系的两个条件想起,在比较中进一步明确不同过程或方法的共性,从而对具体、感性的经验提升为较为理性的认识,使学生从更上位的层次去感悟策略应用的过程,感受策略的广泛适用性,体验策略的意义和价值,增强运用策略的自觉性。
【参考文献】
[1]姚美芳.凸显策略特点丰富学生体验[J].小学数学教育,2015(9):39-40
[2]徐友新.“解决问题的策略”内容本质和教学价值[J].小学数学教育,2016(Z4):40-42
(江苏省南通市新区学校,江苏南通226000)

