具有非局部时滞和阶段结构的反应扩散系统的行波解

陈清婉，柳文清

具有非局部时滞和阶段结构的反应扩散系统的行波解

陈清婉，柳文清

（闽南科技学院 通识教育学院，福建 泉州 362300）

研究了一类具有非局部时滞和捕食者具有阶段结构的捕食-食饵模型．运用交叉迭代方法和Schauder不动点理论，通过构造上下解，证明了连接零平衡点和正平衡点的行波解的存在性．

非局部时滞；阶段结构；行波解

1　引言及预备知识

在现实中，时滞和空间扩散现象是普遍存在的，在生物种群中，时滞一般用来表示资源再生时间、成熟周期和反馈间隔时间等[1-4]． 非局部时滞由于能更准确反映种群的动力学行为，受到越来越多的关注． 由于种群在空间上分布得不均匀，这就导致了种群在空间中的扩散，通常在数学上用Laplacian项来表示[5-8]．为了探讨非局部时滞和空间扩散的综合影响，许多学者建立了具有非局部时滞的反应扩散模型[9-12]．

文献[13]研究了一类食饵具有年龄结构和非局部时滞的反应扩散模型

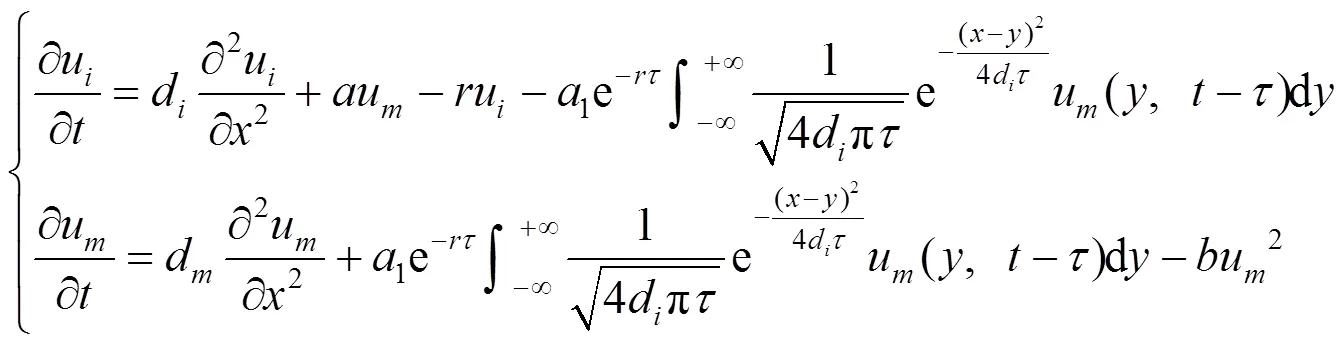
分析了系统（1）的全局动力学性质及波前解的存在性．

文献[14]则进一步讨论食饵具有年龄结构和非局部时滞的反应扩散模型

在此基础上，本文研究一类捕食者具有年龄结构和非局部时滞的反应扩散系统

2 行波解的存在性

考虑具有时滞的反应扩散方程

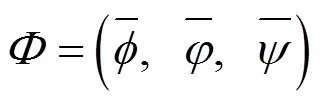
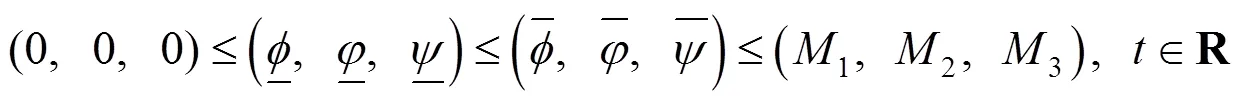
且满足渐近边界条件

直接计算可得

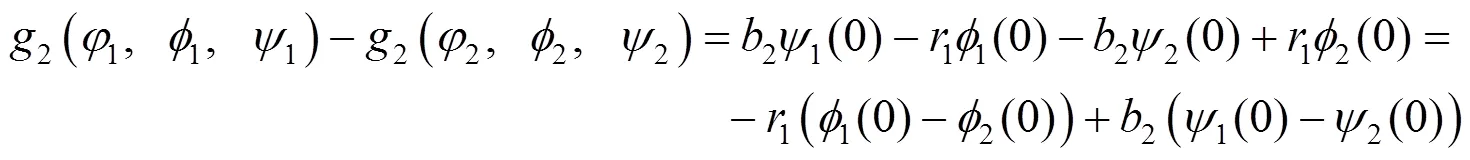
构造函数

由定理1～2及引理可得到连接零平衡点和正平衡点的行波解的存在性结论．

3 结语

本文研究了一类具有非局部时滞和捕食者具有阶段结构的捕食-食饵模型，运用交叉迭代方法和Schauder不动点理论，通过构造上下解，证明了连接零平衡点和正平衡点的行波解的存在性．给出了最小波速，最小波速与扩散率、食饵出生率以及幼年捕食者长成成年转化率成正比．后续的研究中可进一步探讨食饵和捕食者均具有阶段结构的情形，显然这样的模型更符合实际背景．

[1] Gourley S A，So J，Wu J．Non-locality of reaction-diffusion equations induced by delay[J]．J Math Sci，2004，124（4）：5119-5153

[2] 王志丽，徐瑞．一类具有时滞和收获的捕食模型的稳定性和Hopf分支[J]．北华大学学报：自然科学版，2014，15（1）：1-6

[3] 傅金波，陈兰荪，程荣福．具有潜伏期和免疫应答的时滞病毒感染模型的全局稳定[J]．高校应用数学学报：A辑，2015，30（4）：379-388

[4] 黄利航，陈斯养．一类具有时滞的捕食与被捕食模型的Hopf分支[J]．西北师范大学学报：自然科学版，2004，40（4）：12-18

[5] YANG W S，LI X P．Global asymptotical stability for a diffusive predator-prey system with Beddington DeAngelis functional response and nonlocal delay[J]．J Appl Math Comput，2016，50（1）：327-347

[6] 陈清婉 ，柳文清．具有交叉扩散和B-D反应函数的病毒模型的稳定性分析[J]．北华大学学报：自然科学版，2018，19（1）：13-17

[7] 张丽娜，张晓杰．一类捕食者-食饵模型中扩散的作用[J]．应用数学，2016，29（3）：672-677

[8] 柳文清，陈清婉．捕食者食饵均染病的入侵反应扩散捕食系统中扩散的作用[J]．应用数学与力学，2019, 40（3）：89-99

[9] 徐辉军．一类具HollingⅡ型功能反应和非局部时滞反应扩散系统的全局稳定性[J]．数学的实践与认识，2017，47（22）：262-268

[10] 李盼晓．非局部时滞反应扩散方程波前解的指数稳定性[J]．应用数学和力学，2018，39（11）：1300-1312

[11] 王小焕，吕广迎．非局部时滞反应扩散方程行波解的稳定性[J]．数学学报：中文版，2015，58（1）：13-28

[12] Gourley S A，Britton N F．A predator-prey reaction-diffusion system with nonlocal effects[J]．J Math Biol，1996，34（3）：297-333

[13] Gourley A，Kuang Y．Wave fronts and global stability in a time-delayed population model with stage structure[J]．Proc R Soc Lond，2003，459（2034）：1563-1579

[14] ZHANG Xiao，XU Rui．Travelling waves of a diffusive predator-prey model with nonlocal delay and stage structure[J]．J Math Anal Appl，2011，373（2）：475-484

[15] 弗里德曼·A．抛物型偏微分方程[M]．夏宗伟，译．北京：科学出版社，1984

Traveling waves of a reaction-diffusion system with nonlocal delay and stage structures

CHEN Qingwan，LIU Wenqing

（School of General Education，Minnan Science and Technology Institute，Quanzhou 362300，China）

A predator-prey model with a non-local delay and stage structure in predator was studied．By using a cross-iterative method and Schauder fixed point theory，the existence of traveling-wave solutions connecting the zero equilibrium point and the positive equilibrium point was proved by constructing the upper and lower solutions．

nonlocal delay；stage structures；traveling wave

O175.26

A

10.3969/j.issn.1007-9831.2020.04.001

1007-9831（2020）04-0001-05

2020-01-09

福建省教育厅中青年教师教育科研项目（JAT191035，JAT191044）

陈清婉（1986－)，女，福建南安人，讲师，硕士，从事非线性偏微分方程研究．E-mail：lwq84815@163.com