双层优化的多无人机合作式冲突探测与解脱
付其喜,梁晓龙,张佳强,侯岳奇
(1.陕西省电子信息系统综合集成重点实验室(空军工程大学),西安 710051; 2.中国人民解放军94582部队,河南 驻马店 463200)
无人机(unmanned aerial vehicle,UAV)在基础设施监测、货物运输、精准农业和搜索营救等方面得到了广泛应用[1].随着应用的不断拓展,无人机在非隔离空域中运行的需求日益增加[2].无人机在非隔离空域中一旦发生空中相撞事故将酿成灾难性的后果,所以冲突解脱问题成为亟待研究的重点[3].
无人机的短期冲突解脱在未来的无人机交通管理系统(unmanned aircraft systems traffic management,UTM)中具有重要地位.文献[4]提出了导航函数法,既考虑了安全间隔又兼顾了预先规划的航路点,但是会产生过多额外的飞行距离.文献[5-9]提出并完善了一种双向的分布式优化冲突解脱算法.它的基本思想是冲突双方在解脱过程中处于平等的地位,共同负责完成冲突解脱机动.文献[10]提出了一种选择性速度障碍法,在速度障碍法中借鉴了有人机的目视飞行规则.该方法能够实现有人机/无人机空域飞行规则的兼容,但由于在某些空中态势下冲突双方只有一方负责机动,所以容易产生兜圈的情况,造成了额外的解脱机动消耗.文献[11]提出了一种将集中式优化和双向冲突解脱结合的方法.文献[12-13]拓展和改进了改变速度策略解脱模型,在冲突解脱过程中将非线性航迹考虑在内,并可以通过线性方程来完成解脱方案求解.但方法采用集中式优化,无人机通常采用分布式在线冲突探测与解脱.
本文在无人机双向分布式优化的基础上,提出了一种双层优化的合作式分布冲突解脱的方法.首先分析了无人机的冲突解脱模型,提出了一种基于采样的冲突探测算法,然后考虑了无人机的运动约束条件(运动约束包括飞行包线约束、转弯角度约束和角速度约束等)及无人机的机动消耗,针对多无人机冲突解脱提出了一种双层优化的冲突解脱算法与对应求解过程.最后运用蒙特卡洛法验证了运用双层优化算法进行冲突解脱的安全性.仿真结果表明,该方法能够实现多无人机的双向解脱机动和分布式优化,在保证冲突解脱安全性的基础上减少了解脱机动消耗.
1 冲突解脱模型
1.1 无人机几何模型
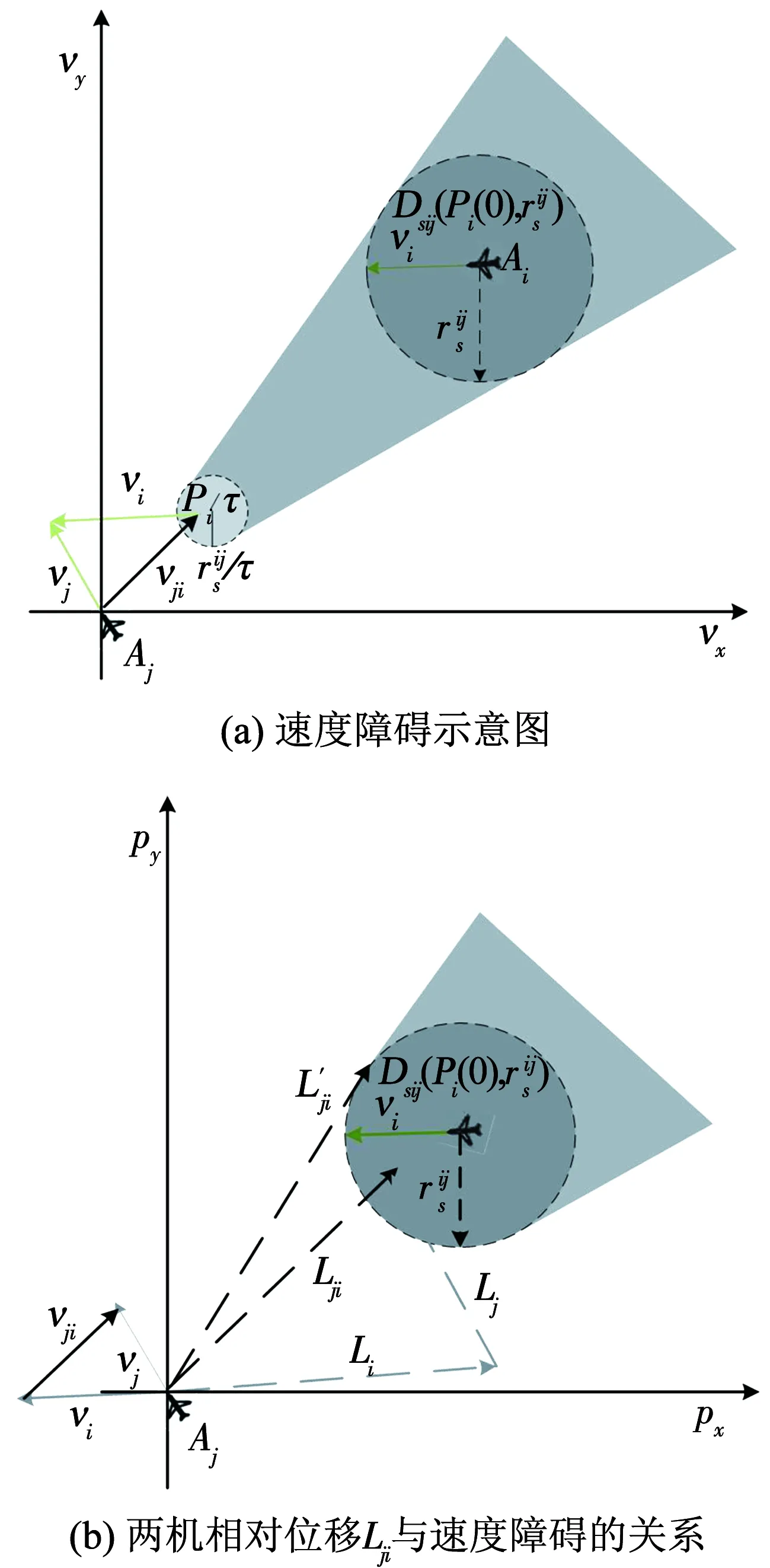
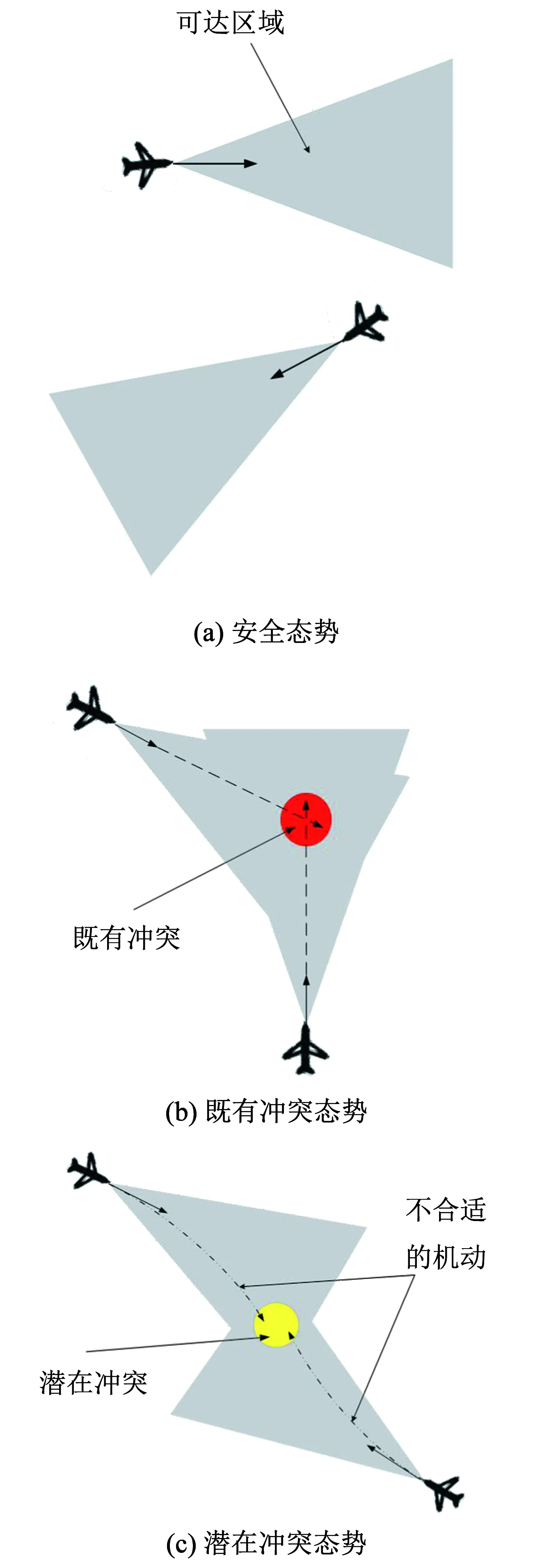
Dsi(pi,ri),i∈N为无人机Ai在二维空间的保护区,即
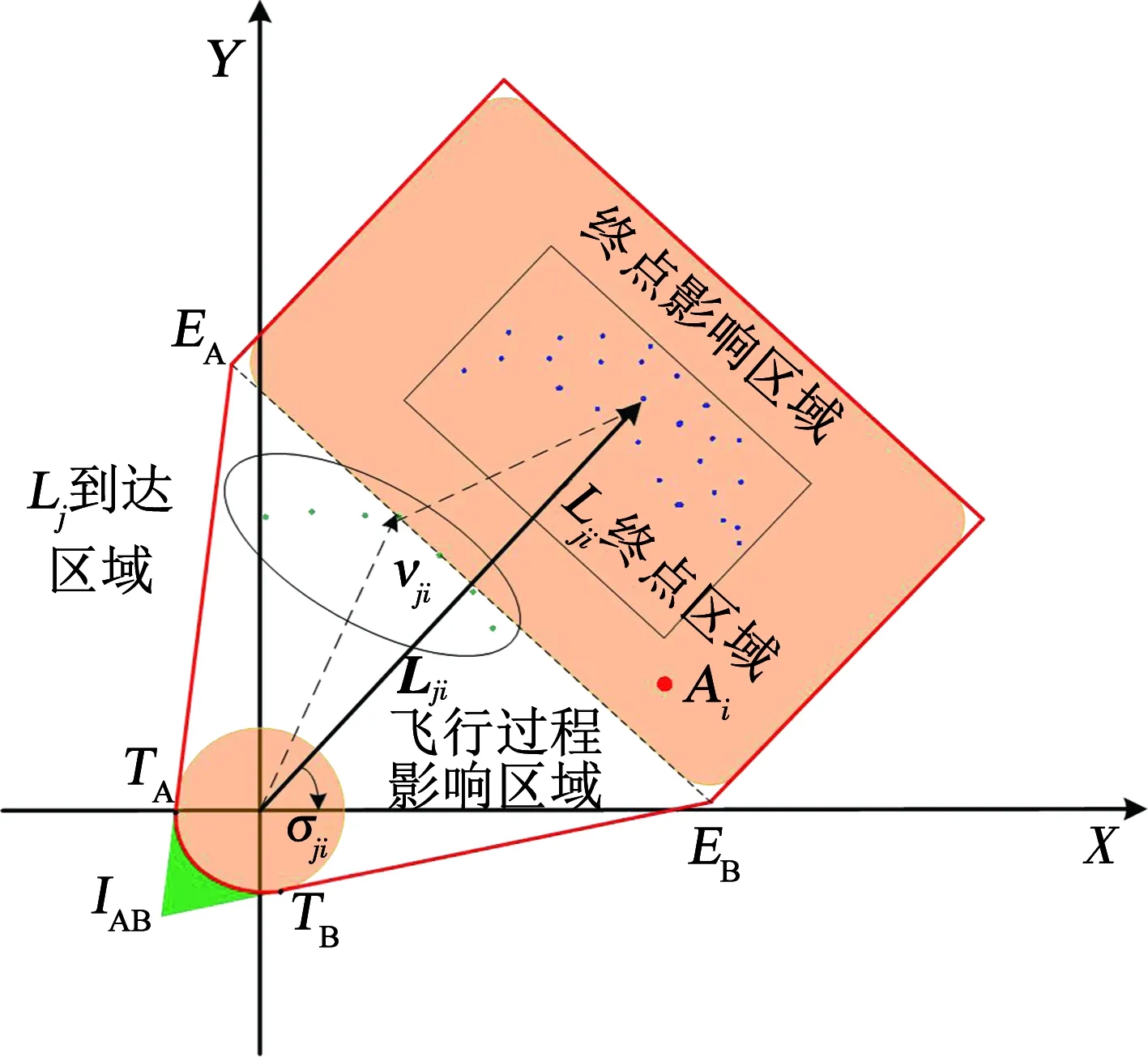
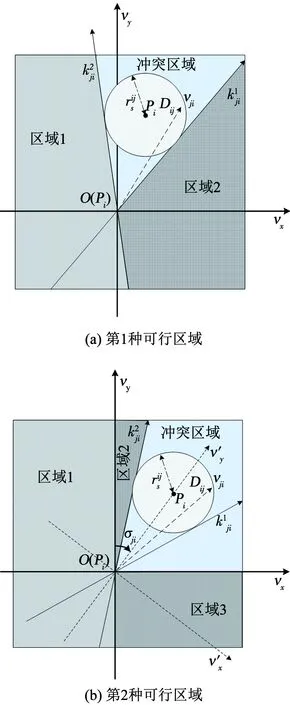
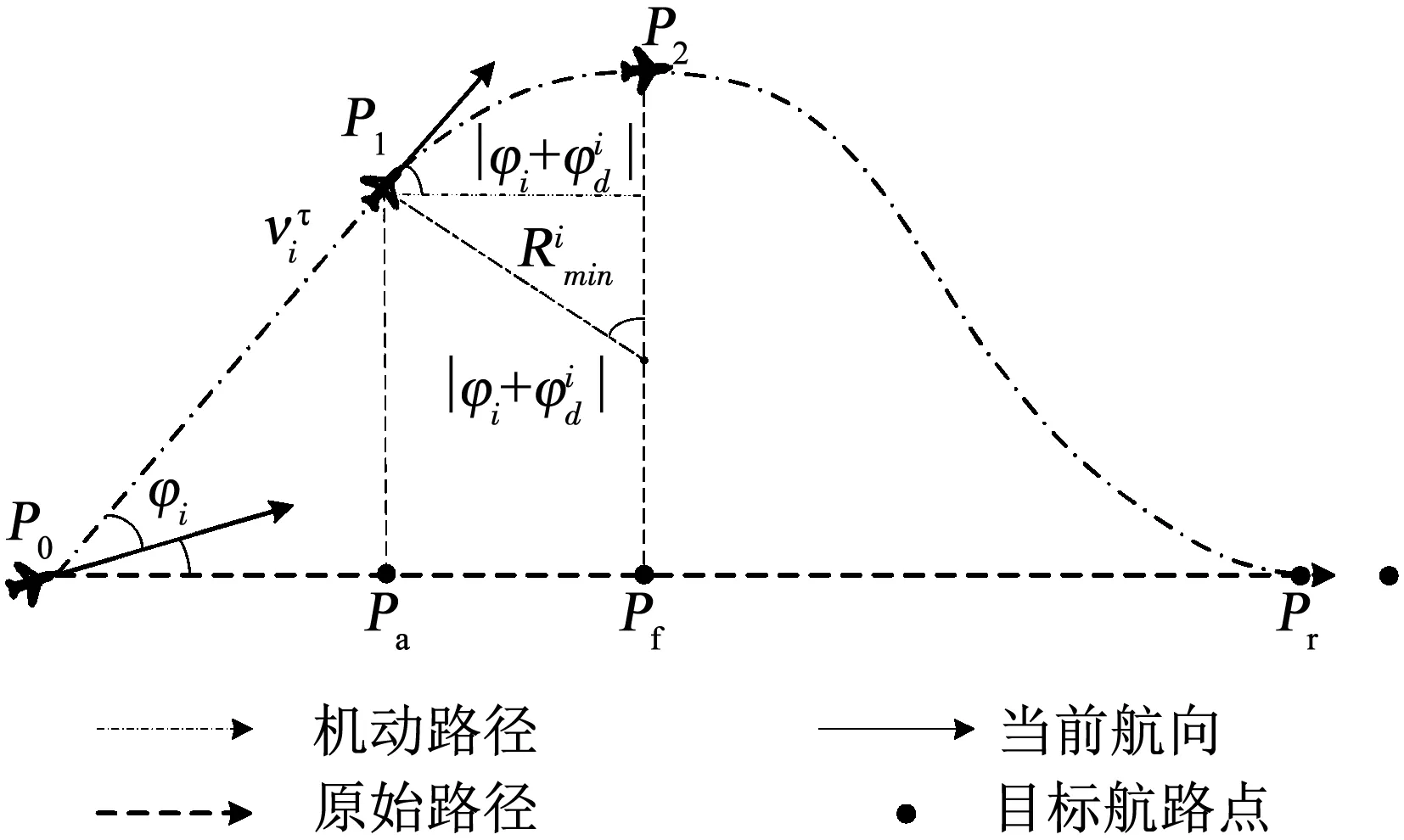
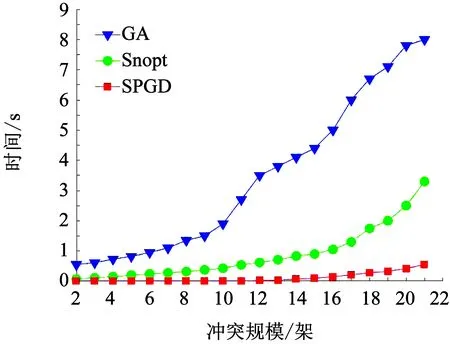
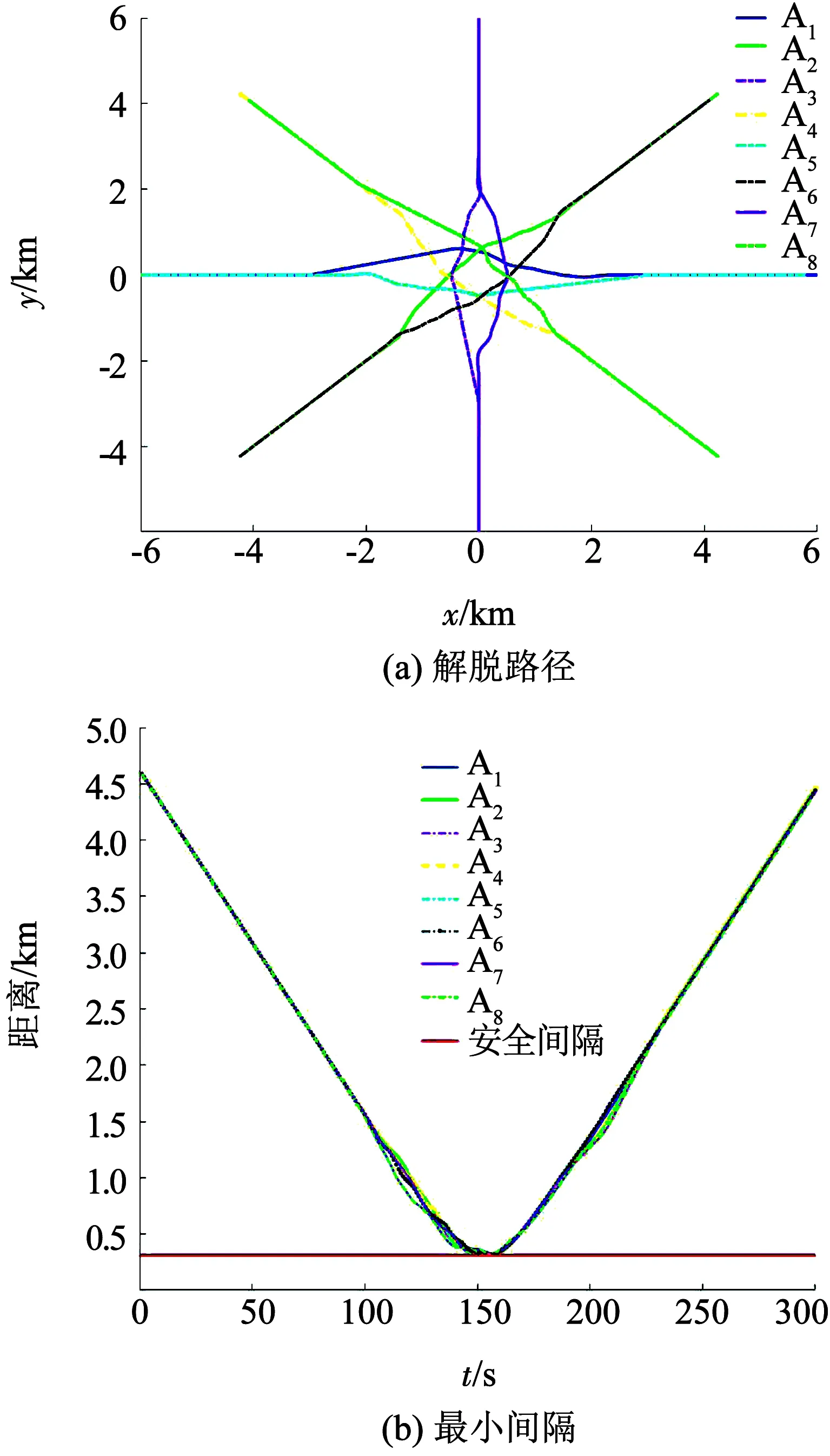
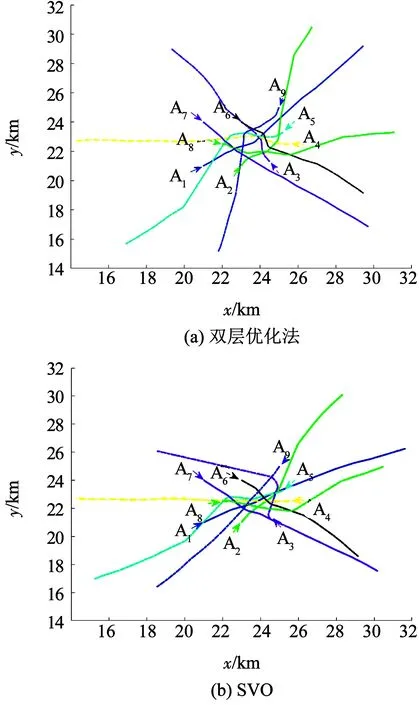
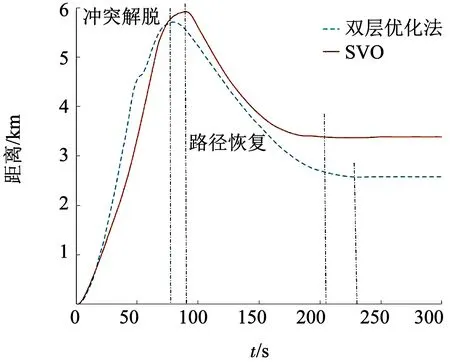
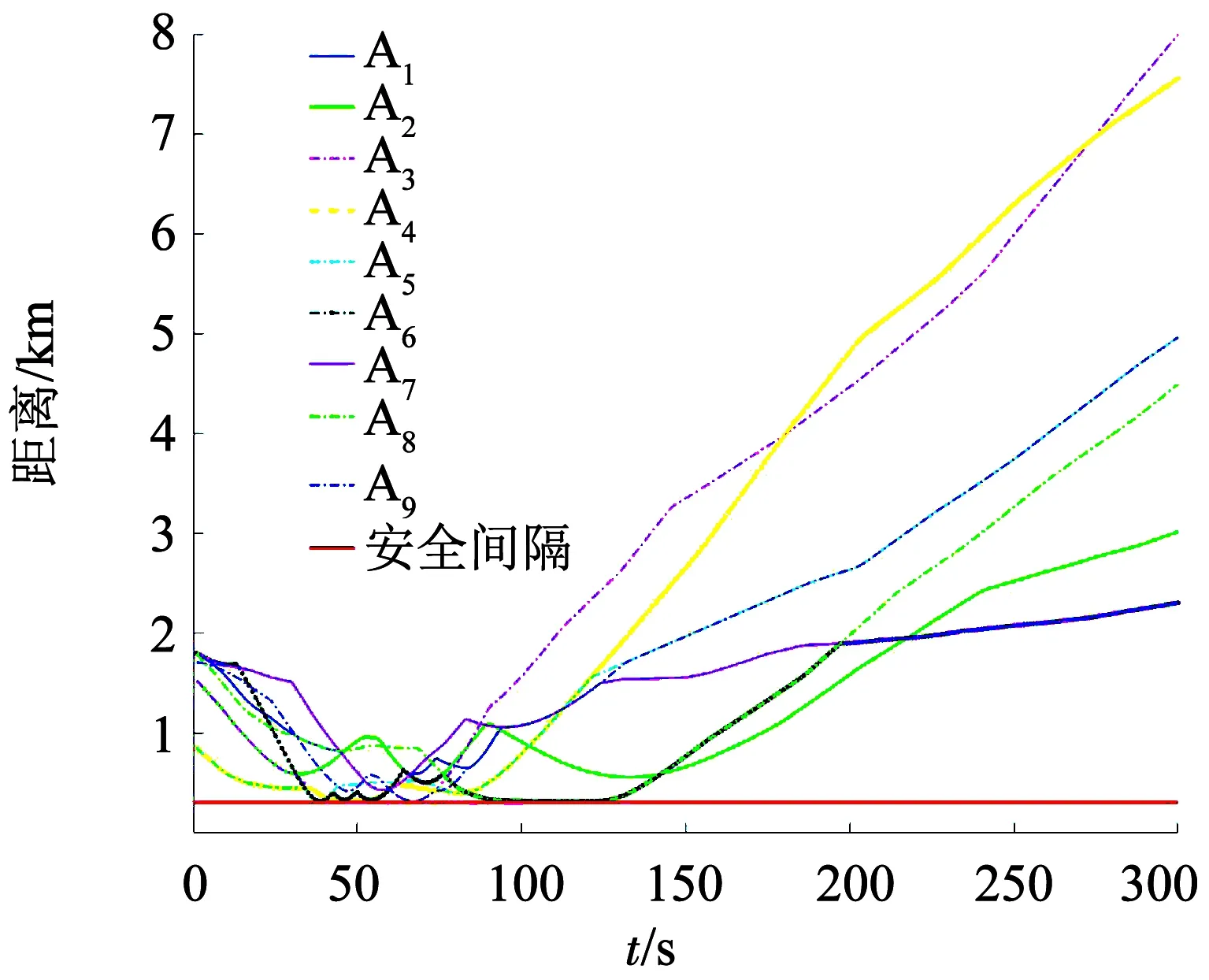
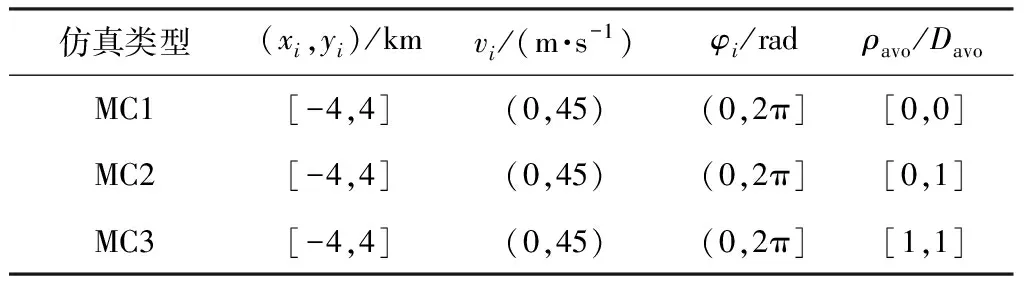
Dsi(pi,ri)={p‖px-xi,py-yi‖ 式中:i为无人机编号;pi=(xi,yi)为Ai的坐标;N为无人机的数量;ri为Ai保护区半径. 本文采用的无人机运动方程为: 0<φi(t)<2π. 本文通过建立局部坐标系来分析无人机的冲突关系,如图1(a)所示,以Aj的当前位置为原点建立局部坐标系.则Ai在t=0时的坐标为 Pi(0)=(xi(0)-xj(0),yi(0)-yj(0)). 假设Ai是静止的,则Aj相对于Ai的速度为 图1 两机速度障碍示意 为了分析无人机位移之间的关系,本文根据速度、位移与时间的关系将速度坐标系转换成位移坐标系,如图1(b)所示.Aj与Ai在τ内的相对位移为Lji=Lj-Li,其中Lj、Li分别为Aj与Ai在τ内的位移,Lj、Li在线规划过程中视为直线.Lji在Aj与Ai进行解脱机动后改变为L′ji,而L′ji应位于Dij之外. 图2中阴影区域为无人机在[0~τ]时间内的可达区域.临近无人机在[0~τ]时间内存在3种态势.图2(a)为两机处于安全态势,在前瞻时间τ内不会发生冲突,图2(b)为两机已经有冲突存在,图2(c)为两机在前瞻时间τ内若进行不合适的机动就会存在冲突的可能.本文将图2(b)、图2(c)分别定义为既有冲突与潜在冲突.在多无人机的冲突解脱过程中,若只考虑既有冲突,则无人机在进行解脱机动时仍会与其他存在潜在冲突的无人机发生冲突,因此本文将潜在冲突与既有冲突均视为存在冲突危险,用crij表示为 为了避免诱发冲突的出现,本文将既有冲突约束与潜在冲突约束视为同一类型约束,这样能够保证多无人机冲突问题在最大范围内求解. 冲突探测算法一般只考虑既有冲突[15-16],双层优化算法根据无人机状态,通过采样进行冲突探测.首先基于位移矢量Lji与前瞻时间τ在无人机的飞行路径上进行预测采样,再根据采样值及无人机位置构建空间区域,最后判断被检测无人机与所构建的空间区域的关系即能进行冲突探测. 二维空间内无人机冲突检测步骤如下. Step1根据无人机Ai与Aj当前的状态以及它们在前瞻时间τ内可机动的角度或速度范围采样在τ时刻相对位移Lji到达的终点散布区域,如图3所示的蓝色散布点. Step2根据无人机Ai与Aj的初始速度和运动方向获得Aj的初始相对速度vji.得到vji与正向X坐标轴之间的夹角σji,将坐标系XOY旋转σji.所有采样点的坐标点在新的坐标系中关于X轴对称.得到采样点集的极值xmax、xmin、ymax、ymin.根据极值点构建一个包含所有终点的矩形区域,将其定义为终点区域,如图3中的黑色矩形框包围的区域. 图2 临近无人机的3种态势 图3 冲突探测示意 Step5产生各类区域后算法采用分区域的方法检测冲突:首先检查Ai的坐标是否在终点影响区域中,然后检查Ai的位置是否在飞行过程影响区域中.在检查飞行过程影响区域时首先检查Ai的坐标点是否在由终点影响区域边界点EA与EB到安全区域圆的切线的交点IAB与EA和EB构成的三角形内,如果在三角形区域中,需要考虑Ai在绿色非威胁区域内的误检测情况. 如冲突解脱几何关系所述,L′ji在[0~τ]时间内应位于Dij之外,将其归结为两个约束条件,即终点约束与切线约束.Ai与Aj在t时刻的距离为 dij(t,φi,φj)=‖Pi(0)-vjit‖, 则无人机在τ的终点约束为 式中:kji为L′ji的斜率;Pix、Piy为Pi(0)的坐标.其中kji的表达式为 式中:kji为周期函数,其定义域为[-π/2+kπ,π/2+kπ],k∈Z;vji的航向范围为H1=[-π/2,π/2]和H2=[π/2,3π/2],这是kji的两个不连续的周期.vji航向的可行区域如图4所示.图4(a)表示的是可行区域的第1种情况,两个可行子区域分别位于kji的两个周期内.图4(b)表示的是可行区域的第2种情况.本文采用旋转局部坐标系的方法将情况1转变为情况2,如图4(b)所示,旋转之后P′ix=0且P′iy>0. 图4 vji航向的可行区域 将由于机动导致的无人机额外飞行距离作为目标函数,记为 图5 冲突解脱机动过程 3)Ai返回原始路径.额外飞行距离为 式中:α为无人机的返回路径与偏离距离的比例系数;β为无人机的返回路径在原始路径上的投影PfPr与偏离距离的比例系数;α、β均为定值. 集中式优化冲突解脱在无人机数量较少时可以取得理想的结果.随着无人机数量的增多,集中式优化冲突解脱难以保证所有无人机的冲突解脱.本文采用分群的思想[17],将多无人机冲突分解为若干无人机冲突群进行分布式冲突解脱. 由于目前能够快速找到局部最优解的算法软件包(如SQP)的计算速度和精度与初始解的好坏有关,所以本文算法采用双层优化的方法获得解脱方案.先采用随机并行梯度下降法(stochastic parallel gradient descent, SPGD)[18]来搜索无人机的初始可行解以得到冲突解脱的可行解区域,然后在可行解区域的基础之上运用序列二次规划(SQP)的方法获得最优解. 运用图论的方法来对多无人机冲突问题进行冲突关系划分.相关无人机的冲突关系用约束图G(t)=(V,E(t))来表示,如图6(b)所示,其中V={1,…,N}为图的顶点集,每一个顶点表示一架无人机.E(t)={(j,i)|cij=1}为表示冲突关系的图的对应边集合.无人机之间冲突关系随时间改变时G(t)也相应改变.无人机之间的冲突矩阵CM可由G(t)的邻接矩阵得到: CM={cm(i,j)=g(φi,φj)ifeij(φi)∈E(t), cm(i,j)=0 else|i,j∈n}. 图6 8机冲突构型 如图6(b)所示,一些无人机之间没有冲突关系.因此,本文提出根据无人机之间的冲突关系将其聚类为若干冲突群,每个冲突群组成一个连通子图.这样空域内的无人机被拆分为若干冲突群,而多无人机冲突解脱问题也就被分解为在每个冲突群内搜索可行的解脱方案,因此可以大大降低算法的复杂度. 产生初始解的随机并行梯度下降算法是一种迭代寻优算法,其流程如图7所示. 图7 随机并行梯度下降法流程 引理1给定一个由nl个无人机构成的冲突簇(nl>2),在局部单调空间中存在能够保证冲突簇中无人机安全间隔可行解区域的前提下,应用SPGD算法求解初始可行解可以保证收敛到该可行区域. 因此,在统计意义上,随机并行梯度下降方法能够找到确保多个无人机安全间隔的初始可行解. 本文已经讨论了解脱机动航向的可行解区域的产生,在此基础上进一步求解机动航向的最优解.基于航向调整的冲突解脱问题是一个非线性优化问题,采用序列二次规划来求解最优解.对于第l个冲突群,其优化目标函数为: s.t.φi=φi(0),vi=vi(0),xi=xi(0),yi=yi(0), 由于每架无人机机动航向的可行区域分为两个子区域,所以对于n架无人机,需要搜索2n个子空间.为保证算法的实时性,当涉及无人机数量较多时,将优化目标降低为搜索若干个子空间内的局部最优解. 为验证SPGD算法的有效性,本文设计了多无人机飞行的冲突场景,在不同规模下分别利用SPGD与遗传算法(GA)和典型的非线性优化求解器(Snopt)进行1 000次冲突解脱解算,并收集了不同数量无人机(2~21)涉及冲突时的算法平均求解时间,将SPGD与遗传算法和Snopt的平均计算时间进行比较,结果如图8所示. 图8 不同算法对比 由图8可以看出,SPGD明显优于Snopt和遗传算法,即使当涉及冲突的无人机数量达到21时,SPGD的求解时间也没有超过0.5 s,能够满足在线求解需要.当涉及冲突的无人机数量小于14时,Snopt的求解时间不超过1 s,但与SPGD相比,明显时间复杂度更高.而遗传算法在求解中明显效率很低,不能满足实时性的要求. 图9(a)显示了8机相同速度相遇时的情况,共同在(0 km,0 km)处遭遇.无人机的速度为40 m/s,复合保护区半径为320 m.图9(b)显示了8架无人机在解脱过程中任意时刻与它机的最小间隔.仿真结果表明8架无人机成功解脱,没有发生冲突,并在解脱完成以后返回到原始路径. 图10比较了双层优化法与选择性速度障碍法(selective velocity obstacle,SVO)在进行多无人机不同速度解脱中的性能.从图10中可以看出,SVO进行解脱时无人机在某些态势下,只有冲突中的一方负责进行解脱机动,这可能导致无人机出现兜圈的情况.而且某些情况SVO会造成无人机进行不可能的机动,比如图10(b)中的无人机A3.图11对两种方法偏离计划位置的距离进行了比较,在初始阶段,由于采用双向解脱方案,双层优化法机动更快,能够首先完成解脱机动.解脱完成之后,双层优化法也能够产生更少的额外飞行距离.无人机之间的最小间隔如图12所示,结果表明双层优化法能够保证无人机在冲突解脱时的安全间隔. 图9 8机相同速度 图10 9机不同速度 图11 偏离计划位置的距离 图12 双层优化法无人机之间的最小距离 Fig.12 Minimum distance between UAVs by two-layer optimization 在上述仿真分析中,多无人机的冲突全部成功解脱.但是,由于无人机在实际运行过程中环境相当复杂,上述的仿真只是基于位置、速度和航向均固定的冲突态势,不能保证算法的普适性.因此,通过蒙特卡洛法产生大量随机的无人机冲突来得到多无人机的冲突概率.与上述类似,本文依然基于小型无人机来进行仿真. 由于现实中的实验具有高风险、耗费高和耗时长的特性,所以本文采用简单、经济、实用的蒙特卡洛法来产生无人机的冲突概率.根据无人机的等效安全水平原则[21],无人机冲突解脱算法的成功率应为100%. 为了评价本文算法的性能,需要设置一些蒙特卡洛仿真的参数.算法的性能可以通过冲突概率Pvio来评价. 式中:Nvio、NMC分别为蒙特卡洛仿真过程中的冲突个数和采样个数;Pvio将随着NMC波动,但随着NMC逐渐增大,Pvio将逐渐趋于一个稳定值. 蒙特卡洛仿真条件如下: 图13 4机随机态势 2)双层优化法中标准无人机解脱开始距离为Davo=τ×vi(τ=25 s).本文在冲突概率分析中考虑解脱开始距离小于Davo的情况,并定义比例系数ρavo为 式中D′avo为仿真中的无人机冲突解脱开始距离.如表1所示,蒙特卡洛仿真采用3种仿真类型:MC1、MC2、MC3. MC1中,ρavo∈[0,0],即不使用冲突解脱算法. MC2中,ρavo∈[0,1],即所有无人机的解脱开始距离D′avo小于标准解脱开始距离Davo.MC3中,ρavo∈[1,1],即所有无人机的解脱开始距离D′avo等于标准解脱开始距离Davo.为了避免无人机的初始间隔对冲突概率的影响,仿真中t=0时无人机的间隔均大于D′avo. 表1 蒙特卡洛仿真参数设置 3)由于小型无人机的规定速度为小于45 m/s,蒙特卡洛仿真中随机产生的无人机初始速度vi∈(0 m/s,45 m/s),且整个仿真过程中无人机的速度保持不变(见表1). 4)为了产生无人机的所有可能相遇态势(对头相遇、交叉相遇和追及相遇),仿真产生的无人机初始航向范围为(0,2π],且在冲突解脱开始之前航向保持不变(见表1). 仿真过程中,首先在正方形区域Asqu中产生N(N=2,3,4,5)架无人机,并根据仿真类型和表1中的参数范围随机产生无人机的位置、速度、航向和比例系数ρavo.若无人机在飞行过程中探测到了冲突存在则无人机运用双层优化法进行冲突解脱,否则无人机航向保持不变. 蒙特卡洛仿真采样次数为106次.仿真结果中的Pvio与采样次数的关系如图14所示,无人机不同数量下的冲突概率如图15所示.由图14、15中可以看出,MC3的冲突概率在2~5机时的冲突概率均为0,符合等效安全水平的要求.MC2中虽然冲突概率比不使用算法的情况下大幅下降,但不能够解脱一切冲突,不满足等效安全水平的要求,解脱失败的原因在于冲突解脱的距离过短. 图14 不同仿真类型的冲突概率 图15 冲突概率对比 通过分析可以得出,在标准的冲突解脱开始距离下双层优化算法的解脱成功率能够达到100%,满足无人机等效安全水平的要求. 1)算法能够解决多无人机的冲突解脱问题,减少解脱代价,满足在线规划需要并降低了对空中交通的影响.可满足无人机等效安全水平的要求,在解脱开始距离Davo=τ×vi(τ=25 s)的情况下能够实现100%的冲突解脱. 2)分析了冲突解脱的几何模型和约束条件,重点研究了冲突几何的终点约束、切线约束和kji的周期性特点,并同时考虑了无人机的既有冲突与潜在冲突,有效避免了诱发冲突,保证冲突解脱问题在最大范围内求解. 3)提出了一种双层优化算法,首先通过随机并行梯度下降法求得冲突群的可行解区域,再用序列二次规划进行最优解的求解,能够在保证成功解脱的情况下进行航向机动的优化. 通过蒙特卡洛法设置不同的仿真条件比较验证了双层优化算法进行多无人机冲突探测与解脱的安全性.
1.2 冲突解脱几何关系
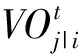
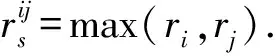
2 冲突探测
2.1 无人机态势

2.2 冲突探测算法
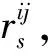
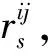
3 冲突解脱约束条件
3.1 解脱机动的约束条件
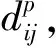

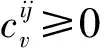
3.2 目标函数
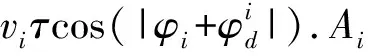
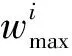
4 双层优化多无人机冲突解脱
4.1 产生无人机冲突群

4.2 SPGD求解可行区域
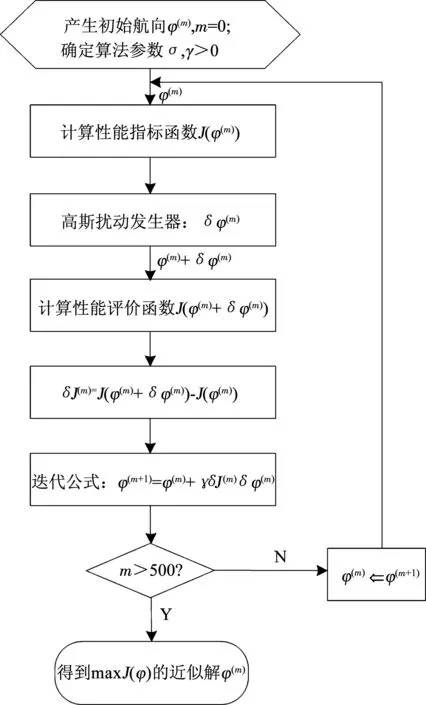
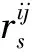
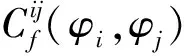
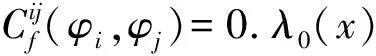

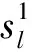
4.3 搜索最优解
4.4 算法对比验证分析
5 仿真分析
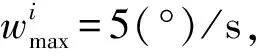
6 蒙特卡洛法冲突概率分析
6.1 蒙特卡洛仿真条件
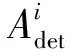

6.2 结果分析


7 结 论

